FTCS Explicit Finite Difference Method for Evaluating European

FTCS Explicit Finite Difference Method for Evaluating European Options CS 757 Computational Finance Project No. CS 757. 2003 W-26 Amit Chhabra Department of Computer Science University of Manitoba 10/7/2020 CS 757 -Project Presentation 1

Outline p p p Introduction and Motivation Problem Statement Solution Strategy n n p Experimental Results n n n p FTCS Method Assumptions Effect of N Effect of Volatility and T Variance of Option Value with K Effect of r Effect of l (Time steps) Conclusion and Future Work 10/7/2020 CS 757 -Project Presentation 2

Introduction and Motivation p The pricing of financial instruments by numerical solutions of their pricing equation has become an important component in the arsenal of techniques available to practitioners of modern quantitative finance. p The demand for complex financial instruments and the availability of powerful computers make the direct numerical solution of the governing pricing equation increasingly appealing approach to pricing 10/7/2020 CS 757 -Project Presentation 3

Problem Statement p The solution methods for the Black-Scholes model (used for the evaluation of option price) are computationally intensive. p Moreover non-linearity of the BS model and real-time solution requirement makes it further difficult to solve the BS model. p Thus, we developed an efficient and fast algorithm for evaluating European Option by Finite Differencing. 10/7/2020 CS 757 -Project Presentation 4

Solution Strategy p We have applied the Forward Time Centered Space (FTCS) method on the Black-Scholes equation to discretize the Partial Differential Equation (PDE). p Assumptions n n n 10/7/2020 The stock price follows the geometric Brownian motion with constant volatility There is a constant risk free interest rate r There are no arbitrage opportunities or transaction costs CS 757 -Project Presentation 5

Solution Strategy cont… p The complete non-linear Burger equation is of the form: p From the Computational Fluid Dynamic (CFD) literature [2, 3] it is known that FTCS method works well for Burger’s equation and hence it could be applied to solve the Black. Scholes equation given by 10/7/2020 CS 757 -Project Presentation 6

FTCS Method p In the explicit formulation of FTCS method, a first-order forward difference approximation and second-order central approximation for the time derivative and the spatial derivatives are used, resp. p Hence, the Finite Difference Equation (FDE) for the Burger’s equation is given by 10/7/2020 CS 757 -Project Presentation 7

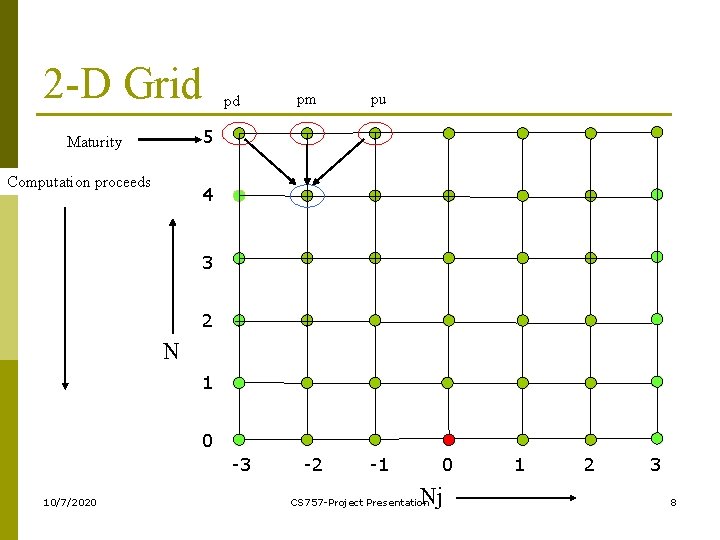
2 -D Grid pd pm pu 5 Maturity Computation proceeds 4 3 2 N 1 0 -3 10/7/2020 -2 -1 0 Nj CS 757 -Project Presentation 1 2 3 8

3 -D Mesh for Evaluating Options 10/7/2020 CS 757 -Project Presentation 9

Experimental Results p To implement the pricing algorithm we used C language on Unix platform. p We studied the effect of various parameters on the option value. p It should be noted that the values of each parameter is varied only when its effect is studied on the option value. 10/7/2020 CS 757 -Project Presentation 10

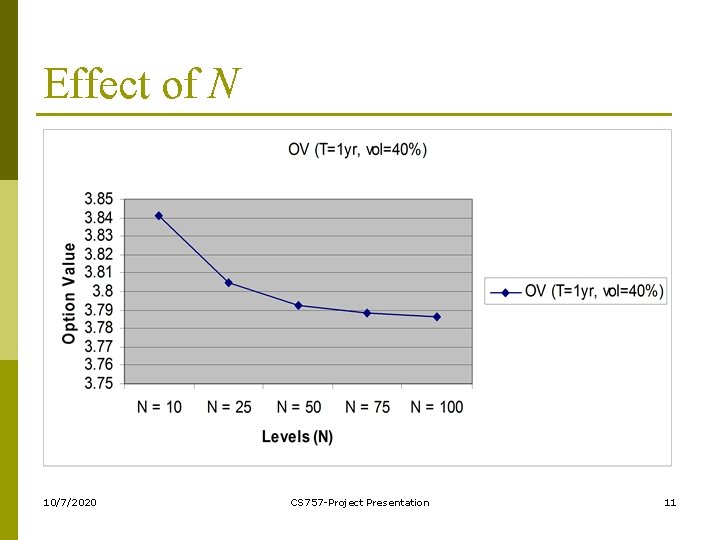
Effect of N 10/7/2020 CS 757 -Project Presentation 11

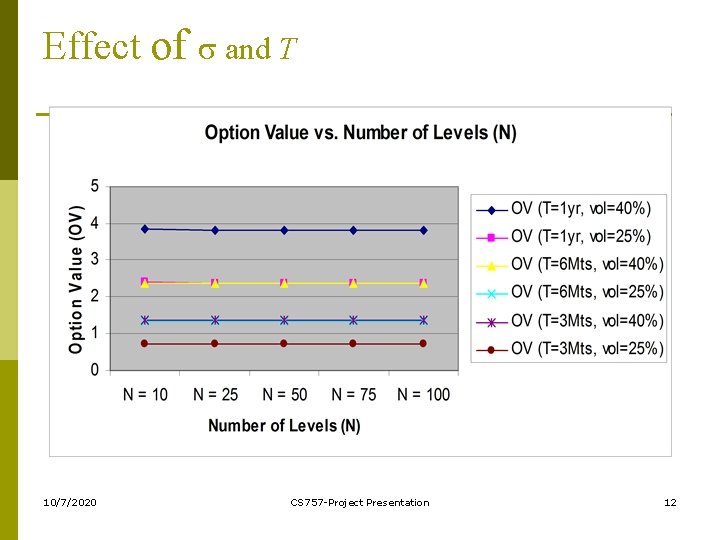
Effect of and T 10/7/2020 CS 757 -Project Presentation 12

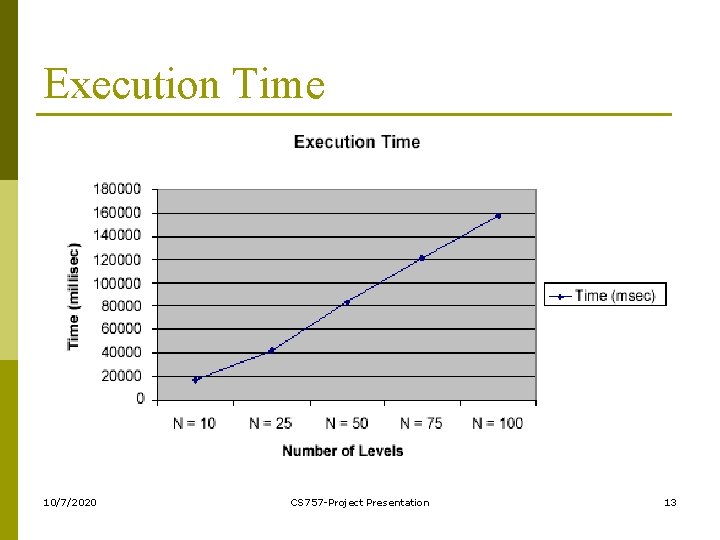
Execution Time 10/7/2020 CS 757 -Project Presentation 13

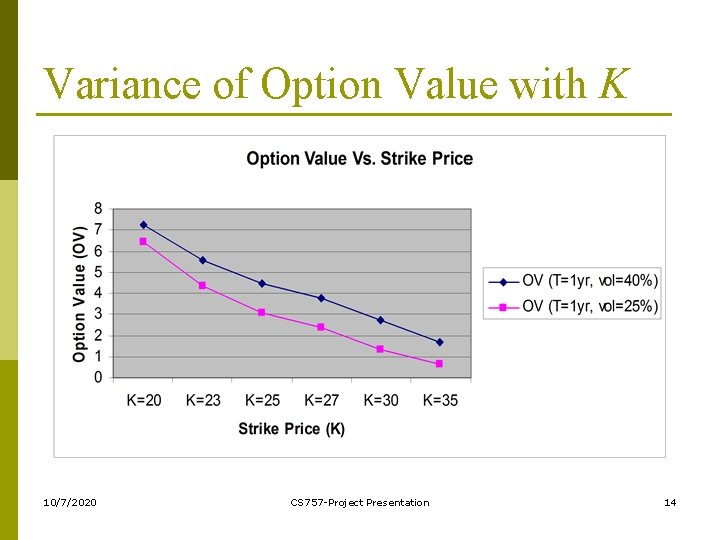
Variance of Option Value with K 10/7/2020 CS 757 -Project Presentation 14

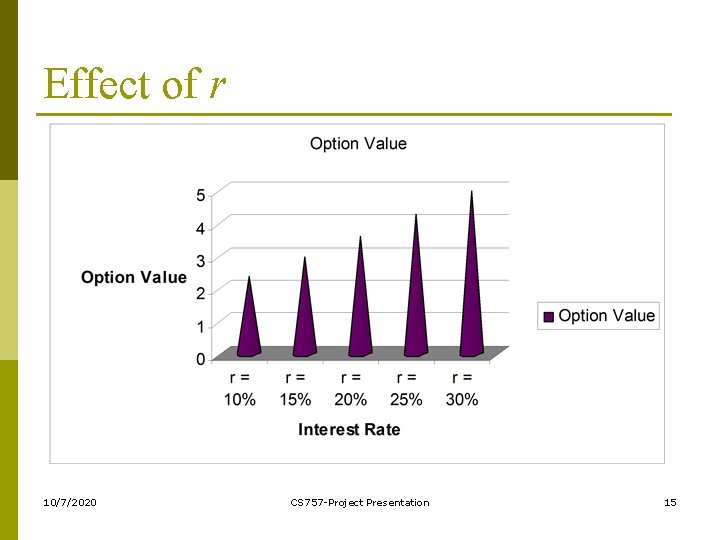
Effect of r 10/7/2020 CS 757 -Project Presentation 15

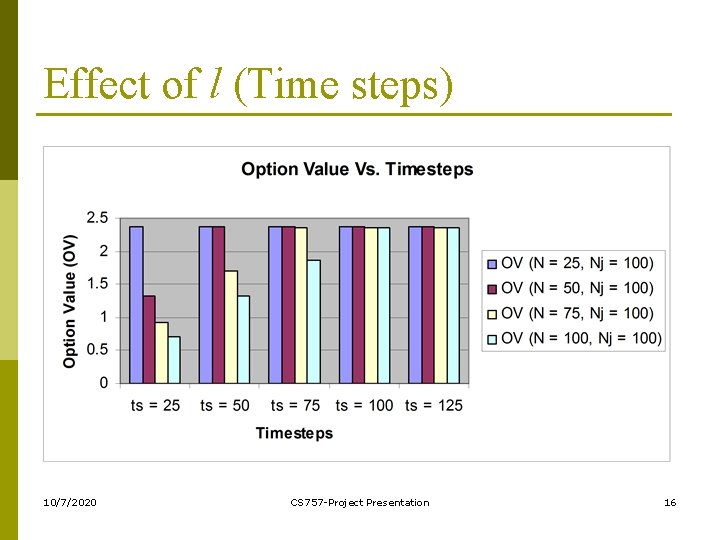
Effect of l (Time steps) 10/7/2020 CS 757 -Project Presentation 16

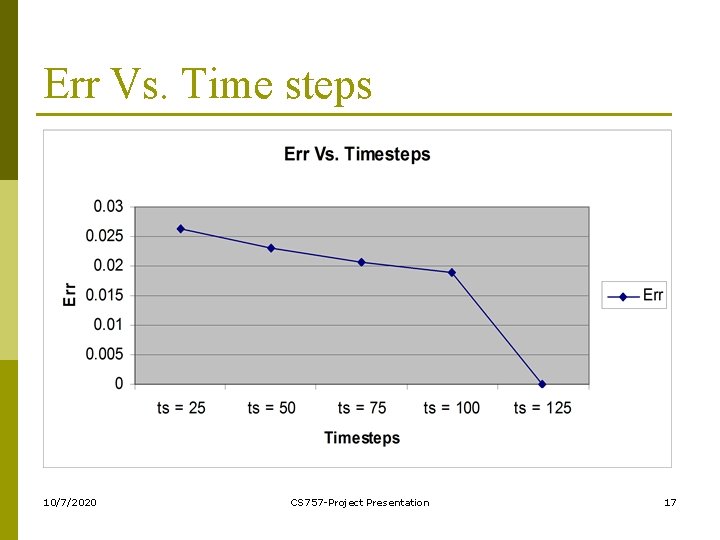
Err Vs. Time steps 10/7/2020 CS 757 -Project Presentation 17

Conclusion and Future Work p p We developed an efficient algorithm fro pricing European options using finite differencing. We studied the effect of various parameters on the value of the option and concluded that increasing the number of time steps increases the accuracy of the option value. Also, after a certain value of time steps the option value stabilizes and err decreases. We considered a dividend paying asset. We notices that for bigger mesh, small machine size is a bottleneck. Hence we intend to parallelize the algorithm to be run on more than one processors and further decrease the execution time. Also, we intend to extend the algorithm for multiple assets. 10/7/2020 CS 757 -Project Presentation 18

Thank You… 10/7/2020 CS 757 -Project Presentation 19