Fsica para Universitrios Mecnica Wolfgang Bauer Gary D


Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Sistemas de partículas e corpos extensos Em nossas discussões anteriores, tratamos sempre da localização de corpos como um único ponto “Um carro está localizado em x = 5, 5 m…” Obviamente o carro não está INTEIRO em x = 5, 5 m A escolha natural para a localização do carro é o seu centro de gravidade O centro de gravidade de um corpo é definido como o ponto no qual podemos imaginar que toda a sua massa esteja concentrada

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias O centro de gravidade Apoiamos um corpo de tal forma que ele fica equilibrado e não gira Existem apenas duas forças A força da gravidade A força do pino que está apoiando o corpo Equilíbrio = as forças são tais que A força resultante é zero O torque resultante é zero => Fg está localizado logo abaixo de ponto de suporte Aqui, o centro de gravidade está marcado com um ponto vermelho
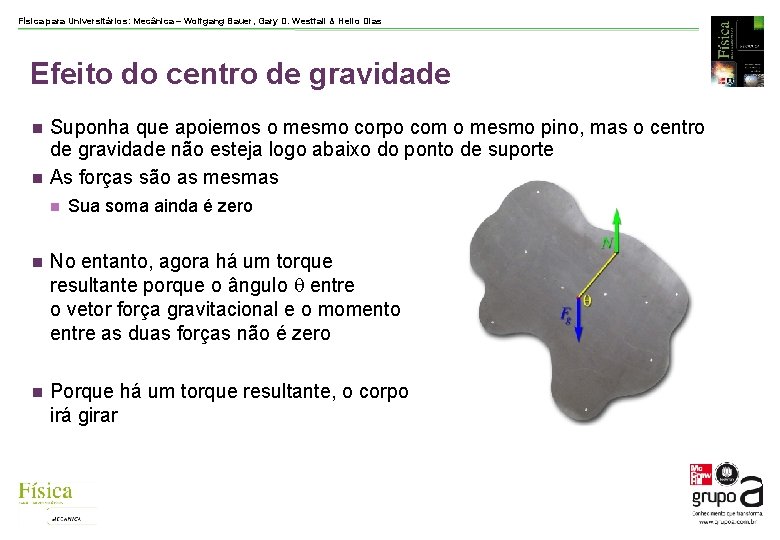
Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Efeito do centro de gravidade Suponha que apoiemos o mesmo corpo com o mesmo pino, mas o centro de gravidade não esteja logo abaixo do ponto de suporte As forças são as mesmas Sua soma ainda é zero No entanto, agora há um torque resultante porque o ângulo entre o vetor força gravitacional e o momento entre as duas forças não é zero Porque há um torque resultante, o corpo irá girar

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Propriedade do centro de gravidade Anteriormente mostramos o vetor força segurando um computador e o vetor força gravitacional apontando para baixo perfeitamente alinhado É claro que se não segurássemos o computador exatamente embaixo de seu centro de gravidade, o computador cairia Podemos concluir afirmando que: Um corpo que não esteja ligado a outros corpos permanecerá em repouso se ele estiver ou sendo segurado exatamente embaixo do seu centro de gravidade ou suspenso exatamente por cima dele

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Determinação do centro de gravidade É possível determinar o centro de gravidade de um corpo com um experimento Primeiro, penduramos o corpo em um ponto arbitrário Em seguida, desenhamos uma linha vertical para baixo Então penduramos o corpo em um segundo ponto arbitrário diferente Desenhamos uma segunda linha vertical para baixo Onde as dua linhas se encontram está o centro de gravidade

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Centro de massa de um sistema de massas Definimos o centro de gravidade de um sistema de n massas como y m 2 m 1 r 2 R r 4 m 3 r 3 m 4 x

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Centro de gravidade de dois corpos Vamos observar um sistema com dois corpos Há equilíbrio se Temos o centro de massa de m 1 e m 2

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Demonstração - empilhamento de blocos Podemos usar a definição de centro de gravidade para produzir um resultado surpreendente Vamos começar com uma pilha de blocos idênticos Até onde podemos empurrar para fora a borda do bloco principal sem que a pilha de blocos caia?
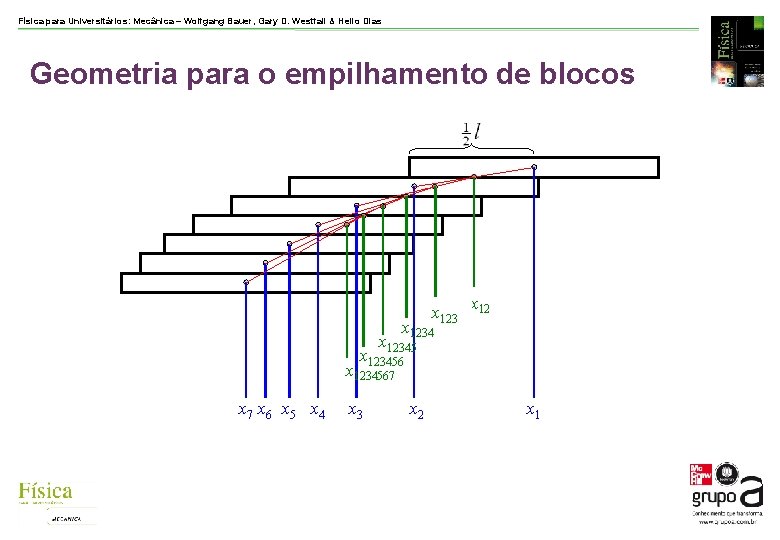
Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Geometria para o empilhamento de blocos x 1234 x 1234567 x 6 x 5 x 4 x 3 x 2 x 1

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Análise do empilhamento de blocos Bloco 1 sobre o bloco 2 Blocks are l long, positions of their center are at x 1, x 2, . . . Some ao bloco 3 Some ao bloco 4 E assim por diante. . .

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Resultado para o empilhamento de blocos Podemos ver para o enésimo bloco Podemos somar todos os termos e obter para n+1 blocos O que significa que podemos estender bastante o bloco de cima

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Exemplo: centro de massa (1) Considere que temos uma placa quadrada e uniforme de metal, com lado L = 3, 40 cm e massa 0, 205 kg. A placa está localizada com seu canto inferior esquerdo em (x, y) = (0, 0) conforme a figura. Nós removemos um quadrado da placa com lado L/4 com o canto inferior esquerdo localizado em (x, y) =(0, 0). Qual a distância do centro de massa da placa restante da origem?
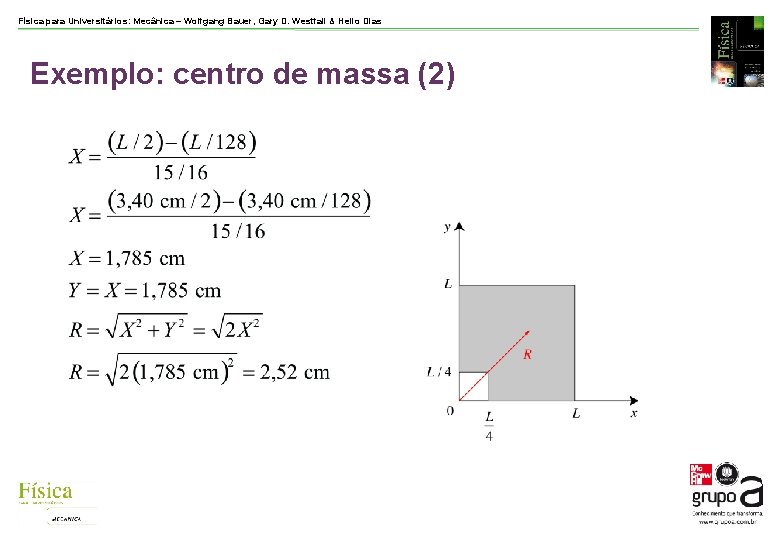
Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Exemplo: centro de massa (2)

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Sistemas coordenados não cartesianos tridimensionais No Capítulo 1, introduzimos um sistema coordenado ortogonal tridimensional Para algumas aplicações é útil representar o vetor posição em sistemas coordenados diferentes Aqui vamos introduz brevemente os dois sistemas coordenados tridimensionais ortogonais mais comumente utilizados O Sistema Coordenado Cartesiano com coordenadas x, y, e z Coordenadas esféricas Coordenadas cilíndricas Em cada um destes casos é preciso especificar um vetor no espaço tridimensional com três valores de coordenadas individuais Nós vamos definir as três coordenadas usadas em cada sistema e mapear estas coordenadas e as coordenadas Cartesianas

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Coordenadas esféricas (1) Nas coordenadas esféricas, o vetor posição é representado por seu tamanho, r, seu ângulo polar relativo ao eixo z positivo, , e o ângulo azimutal da projeção do vetor sobre o plano xy, relativo ao eixo x positivo,

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Coordenadas esféricas (2) Podemos obter as coordenadas cartesianas do vetor das suas coordenadas esféricas pela transformação A transformação inversa, coordenadas cartesianas para esféricas, é

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Coordenadas cilíndricas (1) As coordenadas cilíndricas podem ser vistas como um meio termo entre o sistema cartesiano e as coordenadas esféricas Estamos fixando a coordenada cartesiana z, mas substituindo as coordenadas x e y cartesianas pelas coordenadas r especifica o comprimento da projeção do vetor sobre o plano xy Então r é a distância perpendicular ao eixo z Exatamente como nas coordenadas esféricas, é o ângulo da projeção do vetor no plano xy, relativo ao eixo x positivo.

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Coordenadas cilíndricas (2) Podemos obter as coordenadas cartesianas das coordenadas cilíndricas por Neste caso a transformação inversa de coordenadas cartesianas para cilíndricas é

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Escolha do sistema de coordenadas Como uma maneira prática, você poderia usar um sistema coordenado cartesiano na sua primeira tentativa de descrever qualquer situação física Contudo, os sistemas de coordenadas esféricas e cilíndricas são preferíveis para corpos "arredondados" Mais adiante neste capítulo, faremos uso do sistema de coordenadas cilíndricas para representar uma integral tridimensional de volume No próximo capítulo discutiremos as coordenadas polares, as quais podem ser pensadas como o equivalente bidimensional das coordenadas cilíndricas ou das coordenadas esféricas Depois voltaremos a usar as coordenadas cilíndricas e esféricas para solucionar problemas um pouco mais complicados, que requerem integração.

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Calculando o centro de gravidade Como calculamos o centro de gravidade para um corpo com forma qualquer? Representamos o corpo por pequenos cubos idênticos Cada cubo tem o seu próprio centro de gravidade e podemos calcular o centro de gravidade do sistema de cubos

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Distribuição da densidade e centro de gravidade Obviamente nem todos os cubos no martelo têm a mesma massa A densidade é definida como Se a densidade é uniforme podemos dizer que Se considerarmos que a densidade de cada cubo é diferente, mas que cada um é uniforme podemos dizer que Ao reduzir o tamanho de cada cubo obtemos

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Posição do centro de gravidade Podemos descrever a posição do centro de gravidade de um corpo como Se a densidade for constante em todo o corpo podemos dizer que ou

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Integrais de volume Se quisermos integrar qualquer função sobre um volume tridimensional, precisamos encontrar uma expressão para o elemento de volume d. V em um conjunto de coordenadas apropriado A menos que haja uma razão extremamente importante para não usar, você deveria sempre utilizar sistemas coordenados ortogonais Os três sistemas coordenados ortogonais que vimos até agora, o cartesiano, o cilíndirico e o esférico, são também os únicos em uso na prática

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Integrais de volume em coordenadas Cartesianas É muito mais fácil expressar o elemento de volume d. V em coordenadas cartesianas Então d. V é simplesmente o produto dos três elementos coordenados individuais A integral tridimensional de volume escrita em coordenadas cartesianas torna-se

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Integrais de volume em coordenadas cilíndricas Já que estamos usando o ângulo como uma das coordenadas no sistema de coordenadas cilíndricas, o elemento de volume não tem mais a forma de um cubo Para um dado ângulo diferencial d , o tamanho do elemento de volume depende da distância com relação ao eixo z em que o elemento de volume está localizado A diferencial do volume é A integral do volume então é

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Integrais de volume em coordenadas esféricas Em coordenadas esféricas, usamos dois ângulos variáveis O tamanho do elemento de volume, para um dado valor das coordenadas diferenciais, depende da distância r da origem, bem como do ângulo relativo do eixo = 0 (equivalente ao eixo z das coordenadas cartesianas e cilíndricas). O elemento de volume diferencial nas coordenadas esféricas é A integral de volume é
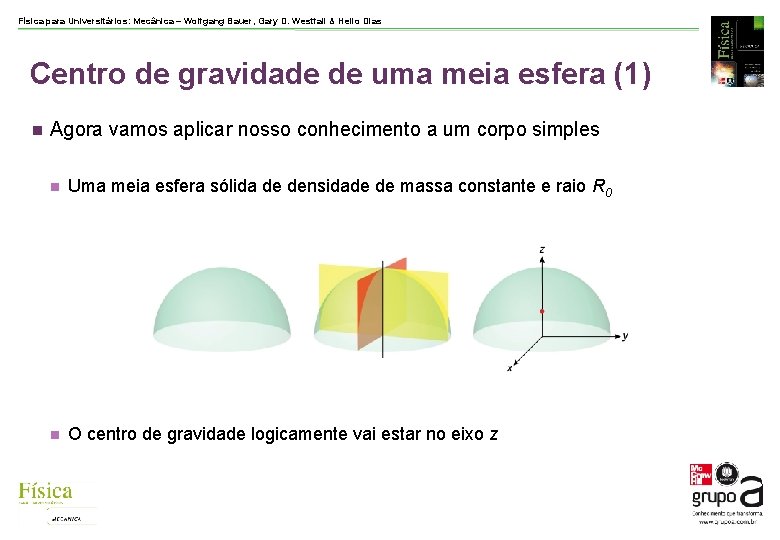
Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Centro de gravidade de uma meia esfera (1) Agora vamos aplicar nosso conhecimento a um corpo simples Uma meia esfera sólida de densidade de massa constante e raio R 0 O centro de gravidade logicamente vai estar no eixo z

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Centro de gravidade de uma meia esfera (2) A coordenada z do centro de gravidade é (densidade constante) O volume da meia esfera é Ficamos com a integral tripla Qual conjunto de coordenadas devemos usar? Coordenadas cilíndricas => a diferencial do elemento de volume é

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Planos de simetria Examine as integrais Digamos que um corpo é simétrico em relação à troca Neste caso, a densidade é uma função precisa de x e os limites são simétricos em relação a x = 0 => a integração nos dá X = 0. No caso de um objeto ser simétrico, o centro de massa deve estar dentro do plano de simetria

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Centro de gravidade de uma meia esfera (3) A integral é E o resultado é

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Exemplo: centro de gravidade #2 (1) Agora vamos enfrentar um corpo mais complicado h=11, 0 cm R=11, 5 cm d=8, 0 cm w=7, 0 cm O lado direito do furo coincide com o eixo central do disco. Um disco ( constante) com um furo retangular Qual é o centro de gravidade deste corpo?
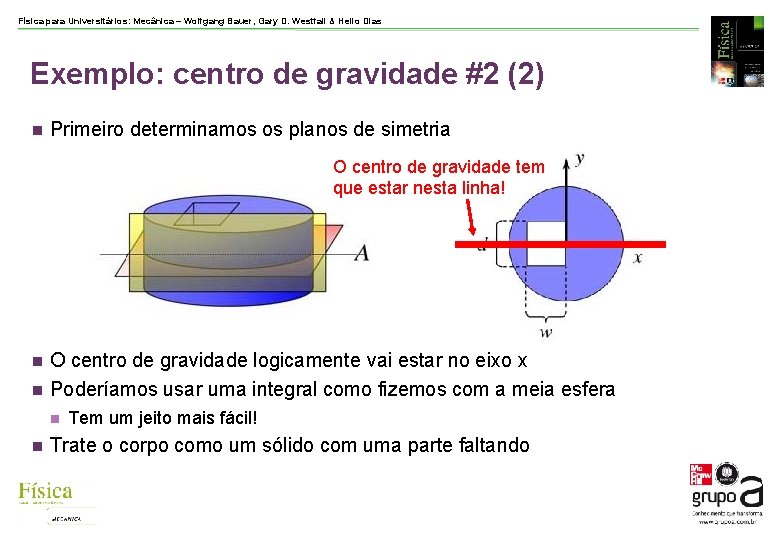
Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Exemplo: centro de gravidade #2 (2) Primeiro determinamos os planos de simetria O centro de gravidade tem que estar nesta linha! O centro de gravidade logicamente vai estar no eixo x Poderíamos usar uma integral como fizemos com a meia esfera Tem um jeito mais fácil! Trate o corpo como um sólido com uma parte faltando

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Exemplo: centro de gravidade #2 (3) Podemos especificar as coordenadas de X como onde cancelamos a densidade Um procedimento elegante: trate a parte que falta como um corpo com densidade negativa Coloque em números:

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Considerações gerais: Note que o centro de gravidade não precisa estar dentro do corpo Exemplo: "Fosbury flop" no salto em altura Dick Fosbury nos Jogos Olímpicos de 1968 na cidade do México

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Movimentos de corpos extensos O movimento de corpos extensos pode parecer complicado Mas se seguirmos o centro de gravidade ao invés de toda a chave-inglesa As coisas ficam mais simples: movimento do centro de gravidade + rotação ao seu redor

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Momento do centro de massa Podemos falar de centro de massa da mesma forma como falamos em centro de gravidade Se não há gravidade, então não há centro de gravidade Sempre há um centro de massa (para a inércia) Podemos descrever o momento do centro de massa começando pelas coordenadas do centro de massa E tomar a derivada referente ao tempo para obter a velocidade E finalmente o momento do centro de massa

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias A segunda lei de Newton para o centro de massa Podemos tomar a derivada temporal do momento para obter a força Observe que a soma das forças exercidas por partículas em outras partículas do mesmo sistema devem ser zero, então temos

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Colisões de dois corpos (1) Conservação de momento e colisões de dois corpos Uma vantagem de pensar em termos de momento de centro de massa anterior como: é que podemos reescrever a lei de conservação O momento do centro de massa não muda com a colisão O resultado se aplica a todos os tipos de colisões

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Colisões de dois corpos (2) Agora introduzimos o conceito de momento relativo de dois corpos Colisão elástica: é conservada Para uma colisão perfeitamente inelástica vimos É a velocidade do centro de massa de um sistema de duas partículas
Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Movimento de recuo Digamos que você dispara uma bala de um canhão O canhão recuará Este efeito é a Terceira Lei de Newton. Este efeito é a conservação do momento Digamos que você esguiche uma grande quantidade de água de uma mangueira de incêndio A mangueira irá recuar A mangueira vai voar e se chicotear como uma cobra se você soltá-la enquanto grandes quantidades de água estiverem passando

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Exemplo: recuo de um canhão (1) Suponha que você dispare uma bala de canhão de massa 13, 7 kg a uma distância de 2, 30 km (seu alcance máximo) do canhão de massa 249, 0 kg. O alvo e o canhão estão na mesma elevação e o canhão está em repouso sobre uma superfície horizontal. Questão: Qual é a velocidade de recuo do canhão?

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Exemplo: recuo de um canhão (2) Resposta: A conservação do momento nos diz (índice 1 para o canhão e 2 para a bala) O canhão pode recuar somente na direção horizontal Então, para a componente horizontal obtemos Sabemos que o ângulo de lançamento é de 45 graus (alcance máximo) e o alcance está ligado à velocidade inicial por

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Exemplo: recuo de um canhão (3) A componente x da velocidade inicial é Ao colocar este resultado de volta na nossa equação de conservação de momento obtemos Inserindo os números obtemos

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Exemplo: mangueira de incêndio Questão: Qual é o módulo da força que atua sobre um bombeiro segurando uma mangueira que ejeta 360 litros de água por minuto, com uma velocidade de saída de 39, 0 m/s? Resposta: Vamos encontrar a massa total de água que está sendo ejetada por minuto A densidade da água é = 1000 kg/litro Porque V = 360 litros de água são ejetado por minuto, temos para a massa total de água ejetada por minuto: O momento da água é então p = v m, e o momento por unidade de tempo é:

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Movimento de foguetes Aqui consideramos um caso em que há variação de massa no objeto em movimento Por exemplo, o ônibus espacial está queimando combustível durante o voo. Um foguete funciona ejetando materiais Estes materiais geralmente são o resultado de uma reação química

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Modelo de foguete (1) Vamos uma nave espacial cuja propulsão seja feita pelo disparo de balas de canhão por sua extremidade traseira Cada bala tem massa m e a massa inicial do foguete é mo Cada bala é disparada com uma velocidade vc relativa ao foguete, resultando um momento da bala de vc m

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Modelo de foguete (2) Após a primeira bala ser disparada, a massa do foguete é reduzida para (mo- m) O foguete recebe um momento de recuo oposto àquele da bala A variação de velocidade do foguete é E a velocidade total do foguete é

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Modelo de foguete (3) Agora disparamos a segunda bala O disparo dessa segunda bala reduz a massa do foguete de (mo- m) para (mo - 2 m), o que resulta em uma velocidade de recuo adicional de

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Modelo de foguete (4) O disparo da enésima bala dá ao foguete a variação da velocidade de Assim, a velocidade do foguete após o disparo da enésima bala é Essa expressão é chamada de relação de recursão Podemos resolver este tipo de equação exatamente de forma numérica Para facilitar, podemos usar uma simplificação bastante justificável

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Modelo de foguete (5) Consideremos que a massa da bala de canhão é pequena se comparada à massa total do foguete, o que nos dá onde vc é a velocidade da bala Agora vamos ao limite de pequenas balas de canhão e obtemos Esta equação diferencial tem a solução

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Modelo de foguete - resposta final Então, se tivermos uma ejeção contínua com velocidade vc de gases provenientes da queima de combustível Considere que o foguete começa com E termina com Massa mi e velocidade vi Massa mf e velocidade vf A variação de velocidade vai ser

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Exemplo: foguete Suponha que temos um foguete com massa de 5, 000 kg sem combustível. Quando o foguete está totalmente abastecido ele tem massa de 205, 000 kg. A exaustão do foguete tem velocidade de 5 m/s. Se o foguete partir do repouso e queimar todo o seu combustível, qual será sua velocidade final?

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Mais foguetes Vamos obter mais informações começando com a segunda lei de Newton para o sistema isolado A taxa de variação de velocidade para a parte m => A taxa de variação de velocidade para a parte dm => Então finalmente obtemos, a partir da segunda lei de Newton,

Física para Universitários: Mecânica – Wolfgang Bauer, Gary D. Westfall & Helio Dias Empuxo de foguetes Chamamos a quantidade de empuxo de um foguete, que é a força exercida pelo propulsor do foguete Podemos calcular a aceleração inicial do ônibus espacial dado que o empuxo é de 31, 3 MN
- Slides: 55