From Raw Data to Physics Reconstruction and Analysis














- Slides: 50

From Raw Data to Physics: Reconstruction and Analysis Introduction Sample Cases A Model Basic Features From Raw Data to Physics Bob Jacobsen August 2006

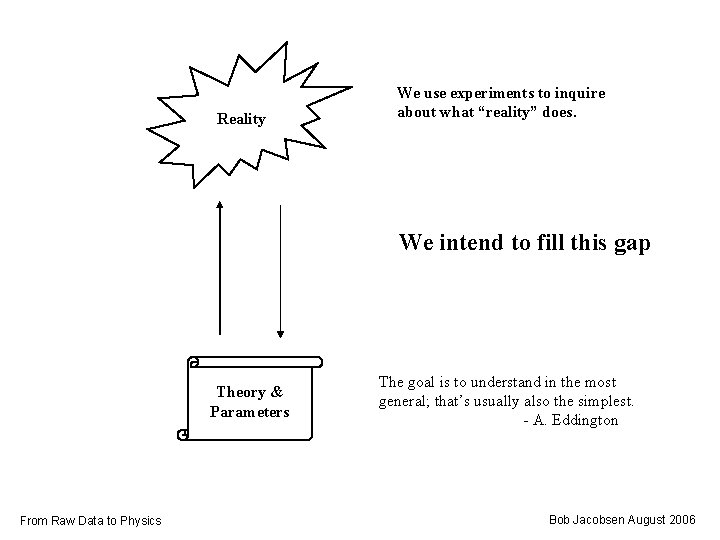
Reality We use experiments to inquire about what “reality” does. We intend to fill this gap Theory & Parameters From Raw Data to Physics The goal is to understand in the most general; that’s usually also the simplest. - A. Eddington Bob Jacobsen August 2006

Theory Particle Data Group, Barnett et al “Clear statement of how the world works” Additional term goes here From Raw Data to Physics Bob Jacobsen August 2006

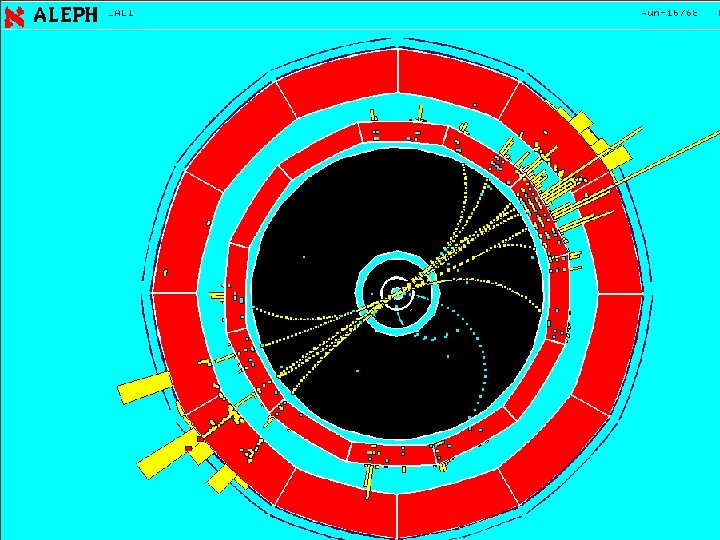
Experiment 0 x 01 e 84 c 10: 0 x 01 e 8 0 x 8848 0 x 01 e 8 0 x 83 d 8 0 x 6 c 73 0 x 6 f 72 0 x 7400 0 x 0000 0 x 01 e 84 c 20: 0 x 0000 0 x 0019 0 x 0000 0 x 01 e 8 0 x 4 d 08 0 x 01 e 8 0 x 5 b 7 c 0 x 01 e 84 c 30: 0 x 01 e 8 0 x 87 e 8 0 x 01 e 8 0 x 8458 0 x 7061 0 x 636 b 0 x 6167 0 x 6500 0 x 01 e 84 c 40: 0 x 0000 0 x 0019 0 x 0000 0 x 01 e 8 0 x 5 b 7 c 0 x 01 e 84 c 50: 0 x 01 e 8 0 x 8788 0 x 01 e 8 0 x 8498 0 x 7072 0 x 6 f 63 0 x 0000 0 x 01 e 84 c 60: 0 x 0000 0 x 0019 0 x 0000 0 x 01 e 8 0 x 5 b 7 c 0 x 01 e 84 c 70: 0 x 01 e 8 0 x 8824 0 x 01 e 8 0 x 84 d 8 0 x 7265 0 x 6765 0 x 7870 0 x 0000 0 x 01 e 84 c 80: 0 x 0000 0 x 0019 0 x 0000 0 x 01 e 8 0 x 5 b 7 c 0 x 01 e 84 c 90: 0 x 01 e 8 0 x 8838 0 x 01 e 8 0 x 8518 0 x 7265 0 x 6773 0 x 7562 0 x 0000 0 x 01 e 84 ca 0: 0 x 0000 0 x 0019 0 x 0000 0 x 01 e 8 0 x 5 b 7 c 0 x 01 e 84 cb 0: 0 x 01 e 8 0 x 8818 0 x 01 e 8 0 x 8558 0 x 7265 0 x 6 e 61 0 x 6 d 65 0 x 0000 0 x 01 e 84 cc 0: 0 x 0000 0 x 0019 0 x 0000 0 x 01 e 8 0 x 5 b 7 c 0 x 01 e 84 cd 0: 0 x 01 e 8 0 x 8798 0 x 01 e 8 0 x 8598 0 x 7265 0 x 7475 0 x 726 e 0 x 0000 0 x 01 e 84 ce 0: 0 x 0000 0 x 0019 0 x 0000 0 x 01 e 8 0 x 5 b 7 c 0 x 01 e 84 cf 0: 0 x 01 e 8 0 x 87 ec 0 x 01 e 8 0 x 85 d 8 0 x 7363 0 x 616 e 0 x 0000 0 x 01 e 84 d 00: 0 x 0000 0 x 0019 0 x 0000 0 x 01 e 8 0 x 5 b 7 c 0 x 01 e 84 d 10: 0 x 01 e 8 0 x 87 e 8 0 x 01 e 8 0 x 8618 0 x 7365 0 x 7400 0 x 0000 0 x 01 e 84 d 20: 0 x 0000 0 x 0019 0 x 0000 0 x 01 e 8 0 x 5 b 7 c 0 x 01 e 84 d 30: 0 x 01 e 8 0 x 87 a 8 0 x 01 e 8 0 x 8658 0 x 7370 0 x 6 c 69 0 x 7400 0 x 0000 0 x 01 e 84 d 40: 0 x 0000 0 x 0019 0 x 0000 0 x 01 e 8 0 x 5 b 7 c 0 x 01 e 84 d 50: 0 x 01 e 8 0 x 8854 0 x 01 e 8 0 x 8698 0 x 7374 0 x 7269 0 x 6 e 67 0 x 0000 0 x 01 e 84 d 60: 0 x 0000 0 x 0019 0 x 0000 0 x 01 e 8 0 x 5 b 7 c 0 x 01 e 84 d 70: 0 x 01 e 8 0 x 875 c 0 x 01 e 8 0 x 86 d 8 0 x 7375 0 x 6273 0 x 7400 0 x 0000 0 x 01 e 84 d 80: 0 x 0000 0 x 0019 0 x 0000 0 x 01 e 8 0 x 5 b 7 c 0 x 01 e 84 d 90: 0 x 01 e 8 0 x 87 c 0 0 x 01 e 8 0 x 8718 0 x 7377 0 x 6974 0 x 6368 0 x 0000 1/30 th of an event in the Ba. Bar detector • Get about 100 events/second From Raw Data to Physics Bob Jacobsen August 2006

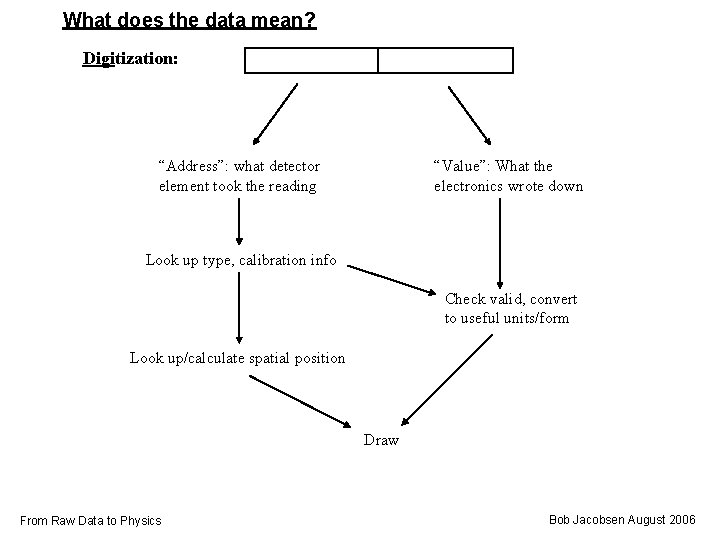
What does the data mean? Digitization: “Address”: what detector element took the reading “Value”: What the electronics wrote down Look up type, calibration info Check valid, convert to useful units/form Look up/calculate spatial position Draw From Raw Data to Physics Bob Jacobsen August 2006

From Raw Data to Physics Bob Jacobsen August 2006

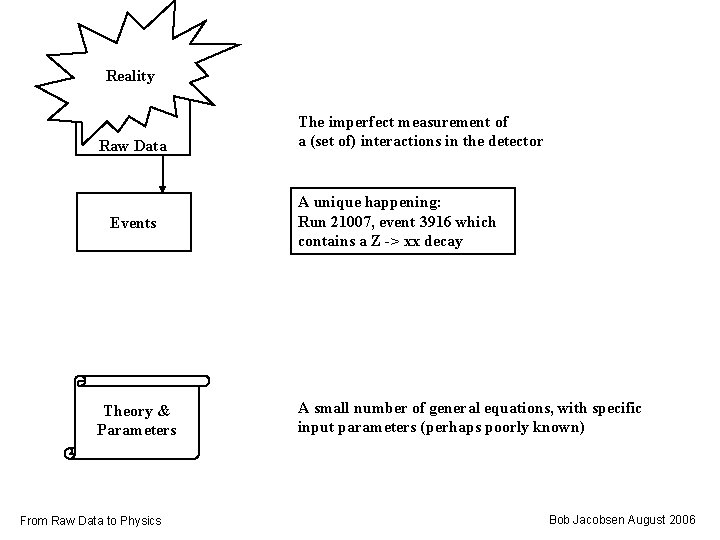
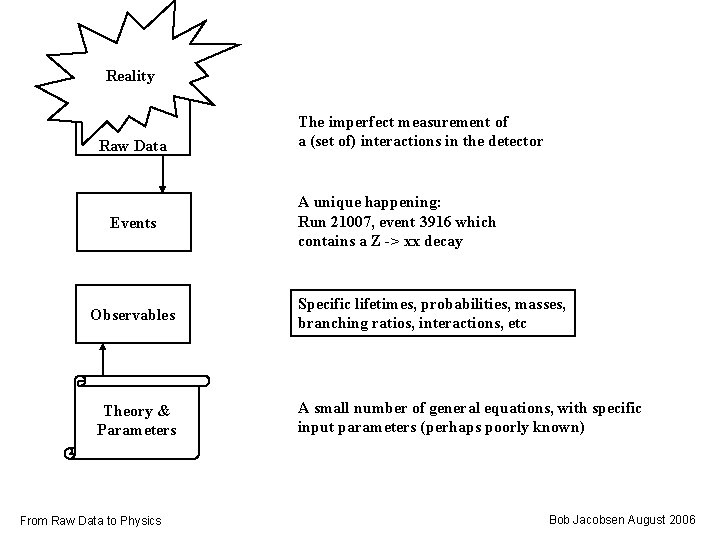
Reality Raw Data Events Theory & Parameters From Raw Data to Physics The imperfect measurement of a (set of) interactions in the detector A unique happening: Run 21007, event 3916 which contains a Z -> xx decay A small number of general equations, with specific input parameters (perhaps poorly known) Bob Jacobsen August 2006

Phenomenology A good theory contains very few numbers But it can predict a large number of reactions Getting those predictions from theory is called “phenomenology” From Particle Data Book Our modified theory predicts a different rate for Z->mm • This gives us a way to prove or disprove it! From Raw Data to Physics Bob Jacobsen August 2006

Reality Raw Data Events Observables Theory & Parameters From Raw Data to Physics The imperfect measurement of a (set of) interactions in the detector A unique happening: Run 21007, event 3916 which contains a Z -> xx decay Specific lifetimes, probabilities, masses, branching ratios, interactions, etc A small number of general equations, with specific input parameters (perhaps poorly known) Bob Jacobsen August 2006

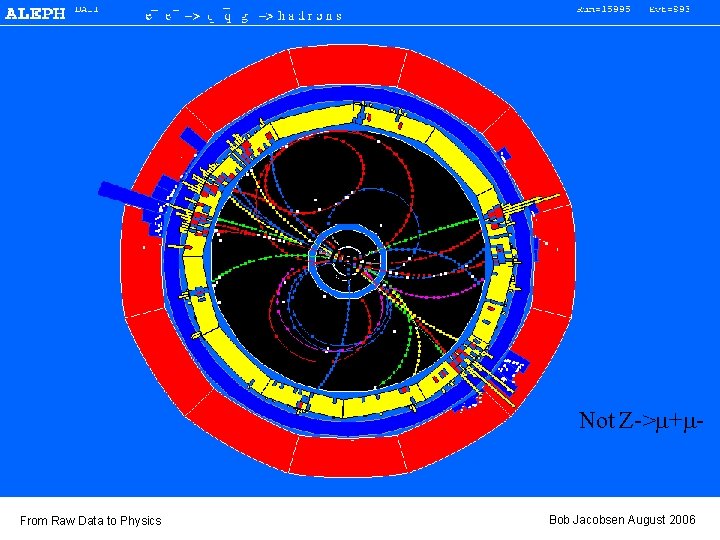
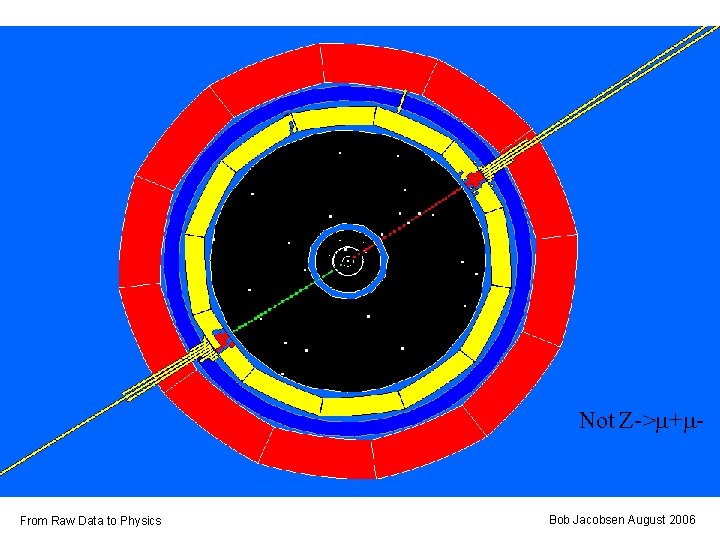
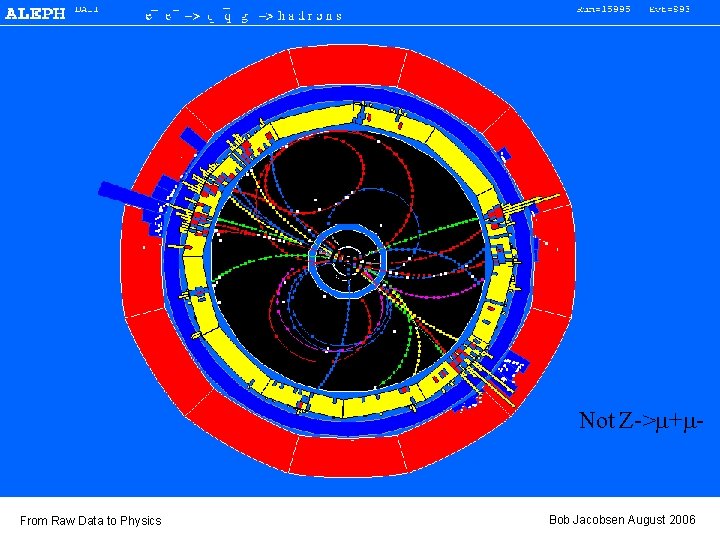
A simple analysis: What’s BR(Z->m+m-)? Measure: Take a sample of events, and count those with a m+m- final state. • Two tracks, approximately back-to-back with the expected |p| Empirically, other kinds of events have more tracks • Right number of muon hits in outer layers Muons are very penetrating, travel through entire detector • Expected energy in calorimeter Electrons will deposit most of their energy early in the calorimeter; muons leave little From Raw Data to Physics Bob Jacobsen August 2006

From Raw Data to Physics Bob Jacobsen August 2006

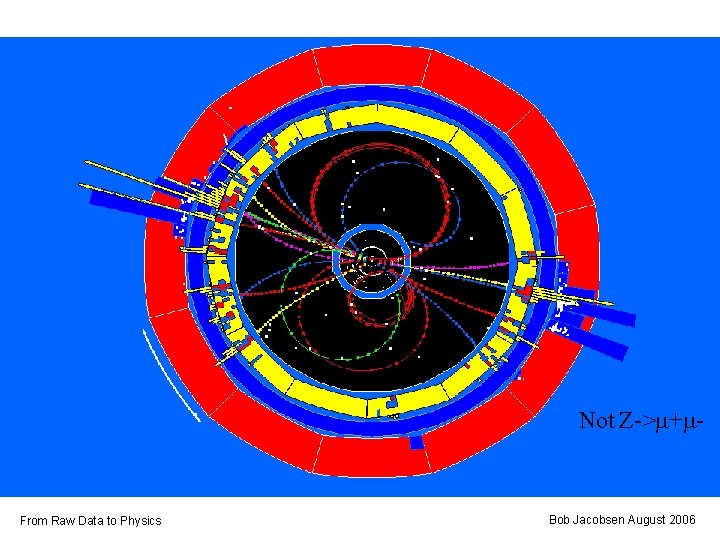
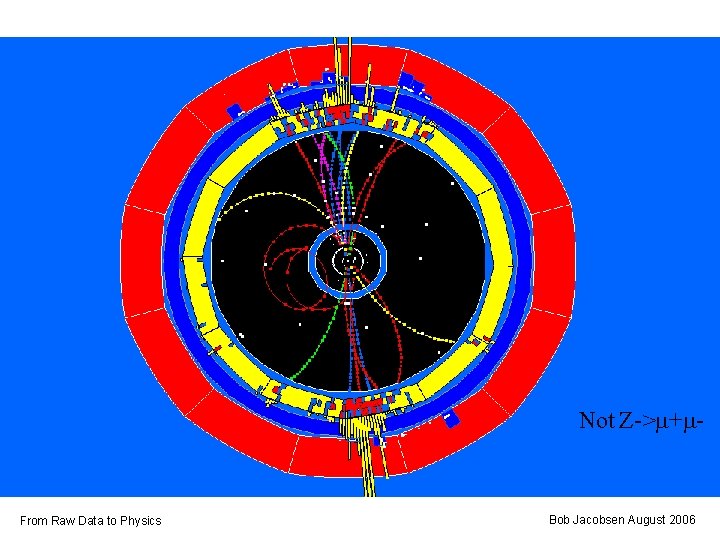
Not Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

Not Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

Not Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

Not Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

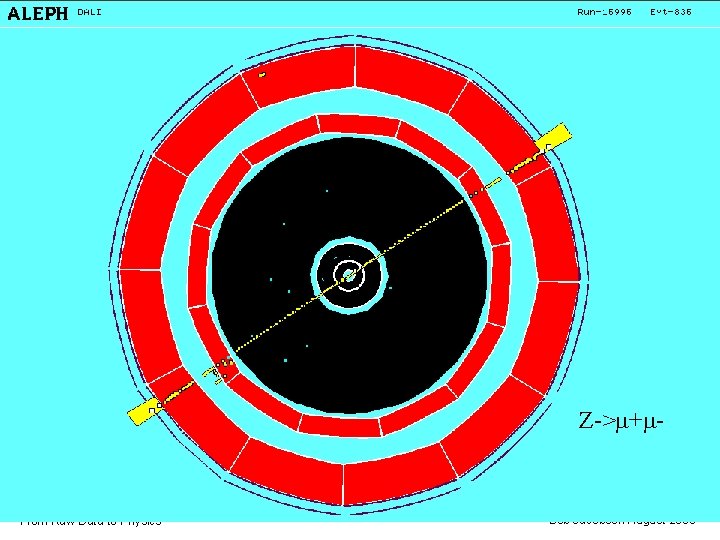
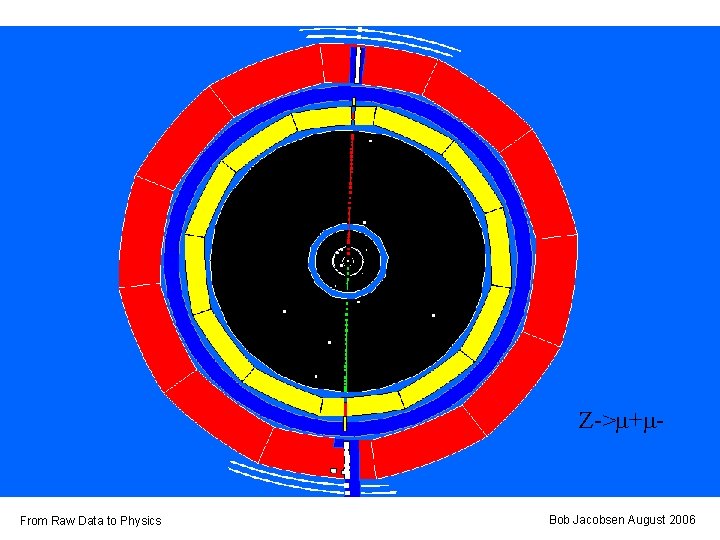
Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

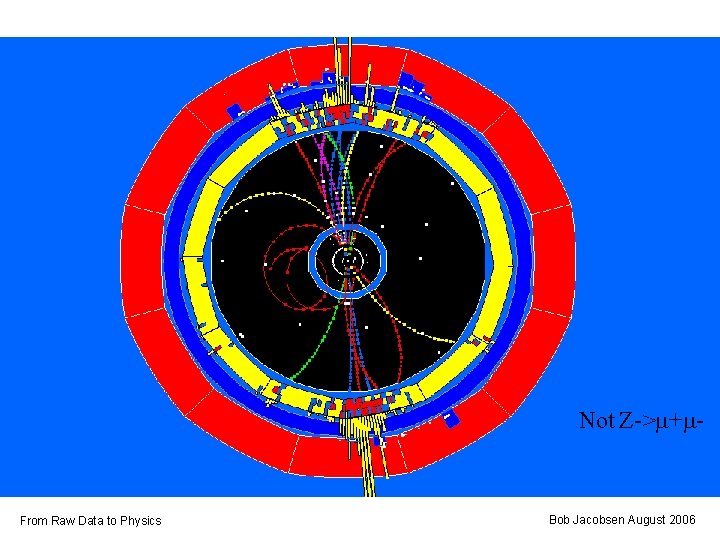
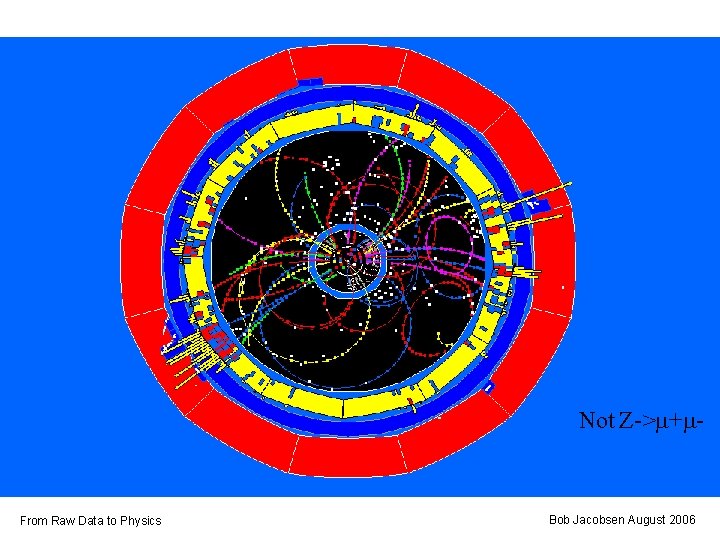
Not Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

Not Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

Not Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

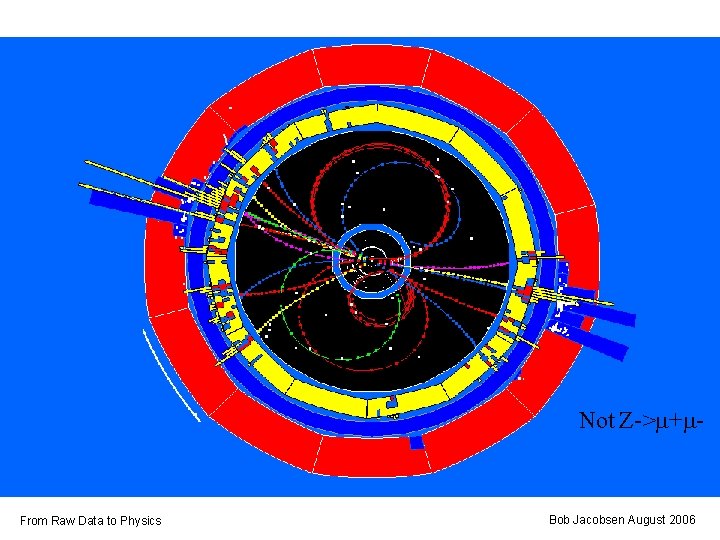
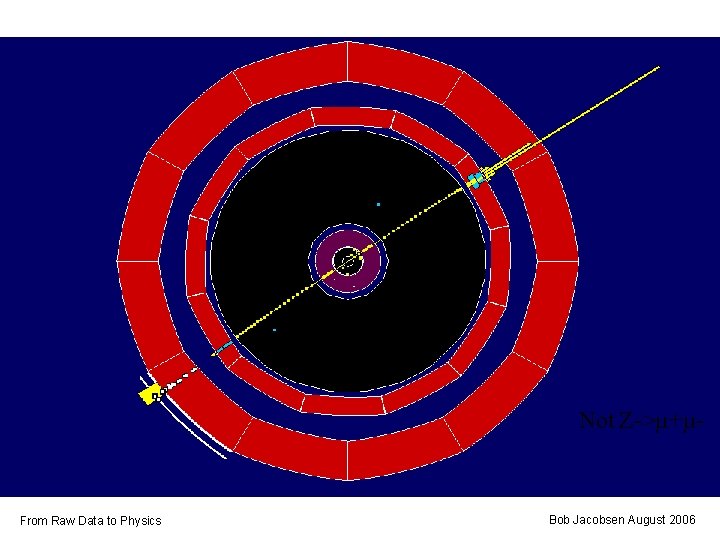
Not Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

Not Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

Not Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

Not Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

Not Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

Not Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

Not Z->m+m- From Raw Data to Physics Bob Jacobsen August 2006

Summary so far We have a result: BR(Z->m+m-) = 2/45 But there’s a lot more to do! Statistical error • We saw 2 events, but it could easily have been 1 or 3 • Those fluctuations go like the square-root of the number of events: • To reduce that uncertainty, you need lots of events Need to record lots of events in the detector, and then process them Systematic error • What if you only see 50% of the m+m- events? Due to detector imperfections, poor understanding, etc? From Raw Data to Physics Bob Jacobsen August 2006

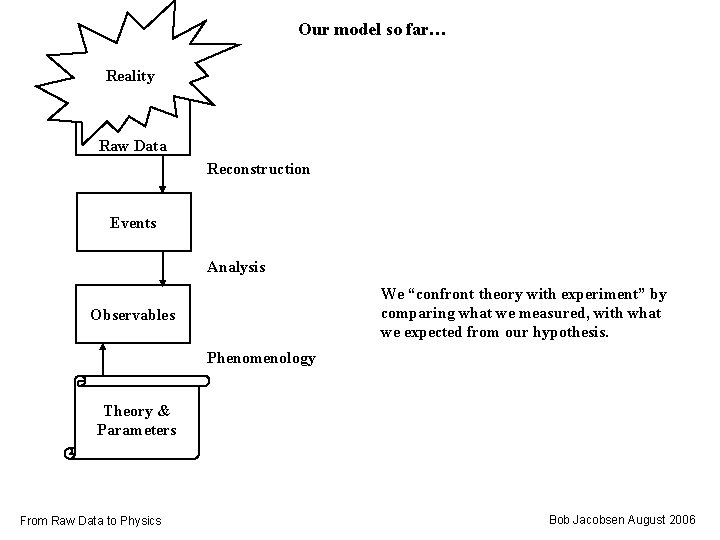
Our model so far… Reality Raw Data Reconstruction Events Analysis We “confront theory with experiment” by comparing what we measured, with what we expected from our hypothesis. Observables Phenomenology Theory & Parameters From Raw Data to Physics Bob Jacobsen August 2006

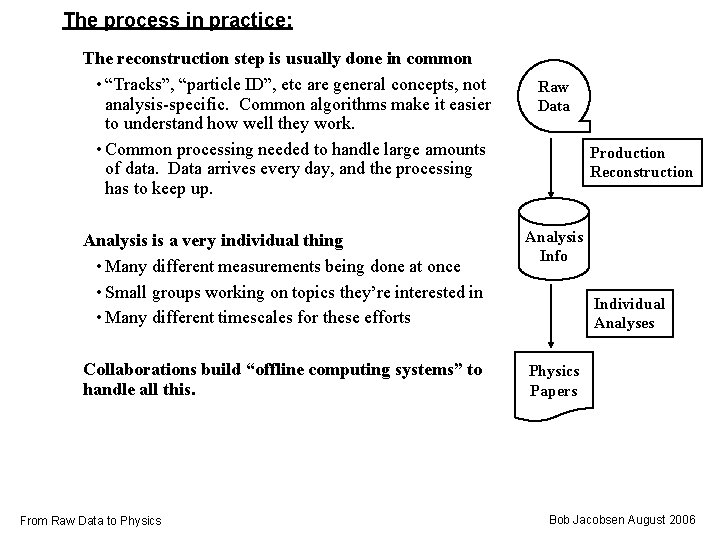
The process in practice: The reconstruction step is usually done in common • “Tracks”, “particle ID”, etc are general concepts, not analysis-specific. Common algorithms make it easier to understand how well they work. • Common processing needed to handle large amounts of data. Data arrives every day, and the processing has to keep up. Raw Data Production Reconstruction Analysis is a very individual thing • Many different measurements being done at once • Small groups working on topics they’re interested in • Many different timescales for these efforts Analysis Info Collaborations build “offline computing systems” to handle all this. Physics Papers From Raw Data to Physics Individual Analyses Bob Jacobsen August 2006

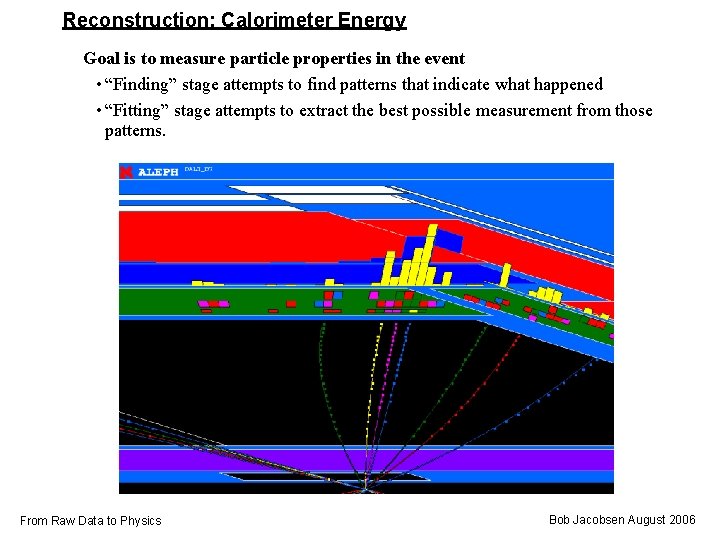
Reconstruction: Calorimeter Energy Goal is to measure particle properties in the event • “Finding” stage attempts to find patterns that indicate what happened • “Fitting” stage attempts to extract the best possible measurement from those patterns. From Raw Data to Physics Bob Jacobsen August 2006

Finding Clusters of energy in a calorimeter are due to the original particles • Clustering algorithm groups individual channel energies • Don’t want to miss any; don’t want to pick up fakes Many algorithms exist • Scan for one or more channels above a high threshold as “seeds” • Include channels on each side above a lower threshold: Not perfect! Doesn’t use prior knowledge about event, cluster shape, etc From Raw Data to Physics Bob Jacobsen August 2006

One lump or two? Hard to tune thresholds to get this right. Perhaps a smarter algorithm would do better? From Raw Data to Physics Bob Jacobsen August 2006

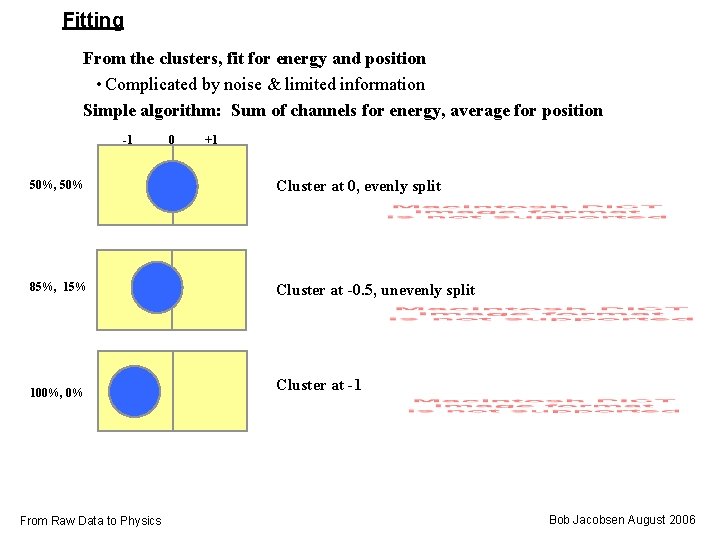
Fitting From the clusters, fit for energy and position • Complicated by noise & limited information Simple algorithm: Sum of channels for energy, average for position -1 0 +1 50%, 50% Cluster at 0, evenly split 85%, 15% Cluster at -0. 5, unevenly split 100%, 0% From Raw Data to Physics Cluster at -1 Bob Jacobsen August 2006

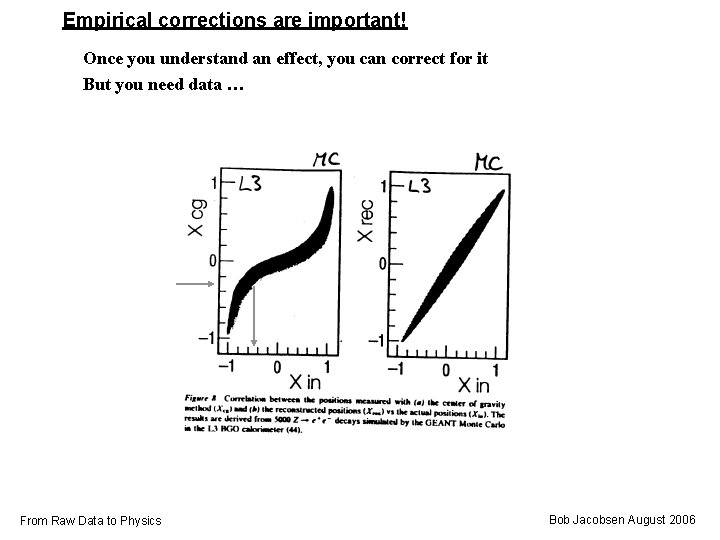
Empirical corrections are important! Once you understand an effect, you can correct for it But you need data … From Raw Data to Physics Bob Jacobsen August 2006

Analysis: Lifetime measurement Why bother? Standard model contains 18 parameters, a priori unknown Particle lifetimes can be written in terms of those “Measure once to determine a parameter Measure in another form to check theory” Measure lots of processes to check overall consistency From Raw Data to Physics Bob Jacobsen August 2006

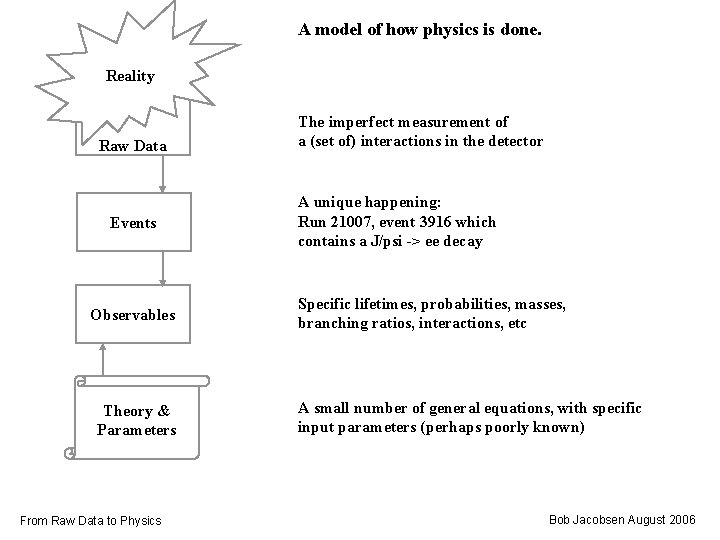
A model of how physics is done. Reality Raw Data Events Observables Theory & Parameters From Raw Data to Physics The imperfect measurement of a (set of) interactions in the detector A unique happening: Run 21007, event 3916 which contains a J/psi -> ee decay Specific lifetimes, probabilities, masses, branching ratios, interactions, etc A small number of general equations, with specific input parameters (perhaps poorly known) Bob Jacobsen August 2006

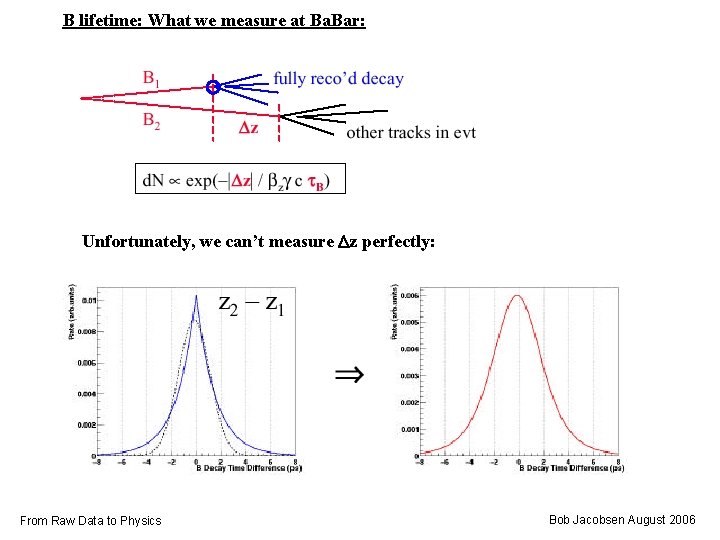
B lifetime: What we measure at Ba. Bar: Unfortunately, we can’t measure Dz perfectly: From Raw Data to Physics Bob Jacobsen August 2006

This is why so much effort is put into “tracking” From Raw Data to Physics Bob Jacobsen August 2006

You also have to find the B vertex To reconstruct a B, you need to look for a specific decay mode (Un)fortunately, there are lots! B 0 -> Each involves additional long-lived particles, which have to be searched for: D*+ -> D 0 pi+ D*0 -> D 0 pi 0 D 0 -> K- pi+, K- pi+ pi 0, K- pi+ pi- pi+, K 0 S pi+ pi- D*+ pi. D*+ rho. D*+ a 1 D+ pi. D+ rho. D+ a 1 J/Psi K*0 bar a 1 - -> rho 0(-> pi+ pi-) pi- rho- -> pi- pi 0 -> gamma Psi(2 S) -> J/Psi pi+ pi-, mu+ mu-, e+ e- J/Psi -> mu+ mu-, e+ e- D+ -> K- pi+, K 0 S pi+ K*0 bar -> K- pi+, K 0 S -> pi+ pi- From Raw Data to Physics Bob Jacobsen August 2006

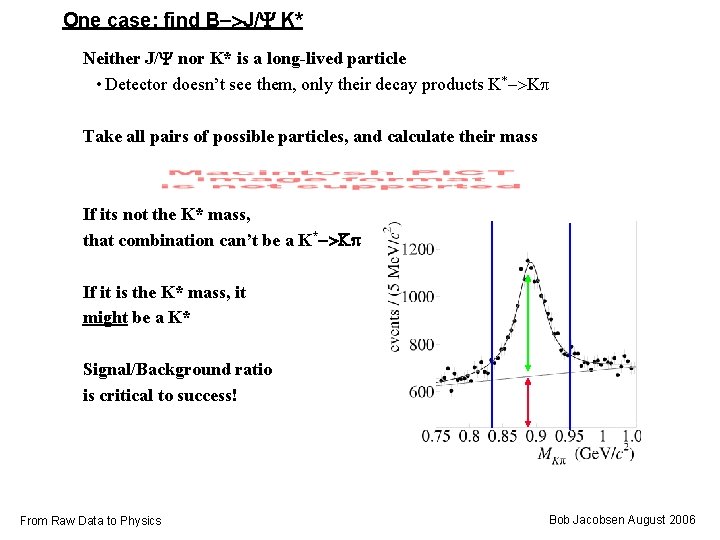
One case: find B->J/Y K* Neither J/Y nor K* is a long-lived particle • Detector doesn’t see them, only their decay products K*->Kp Take all pairs of possible particles, and calculate their mass If its not the K* mass, that combination can’t be a K*->Kp If it is the K* mass, it might be a K* Signal/Background ratio is critical to success! From Raw Data to Physics Bob Jacobsen August 2006

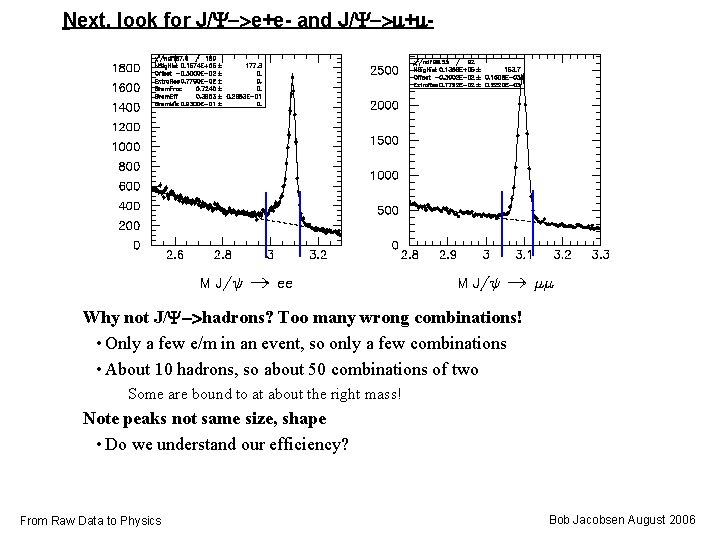
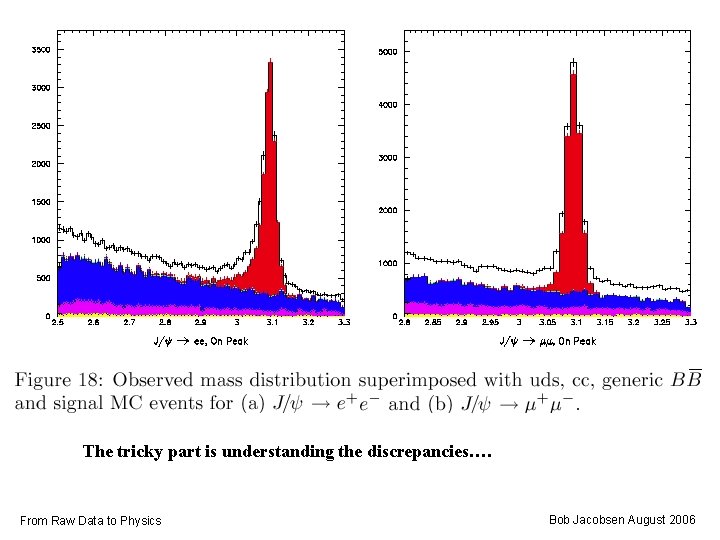
Next, look for J/Y->e+e- and J/Y->m+m- Why not J/Y->hadrons? Too many wrong combinations! • Only a few e/m in an event, so only a few combinations • About 10 hadrons, so about 50 combinations of two Some are bound to at about the right mass! Note peaks not same size, shape • Do we understand our efficiency? From Raw Data to Physics Bob Jacobsen August 2006

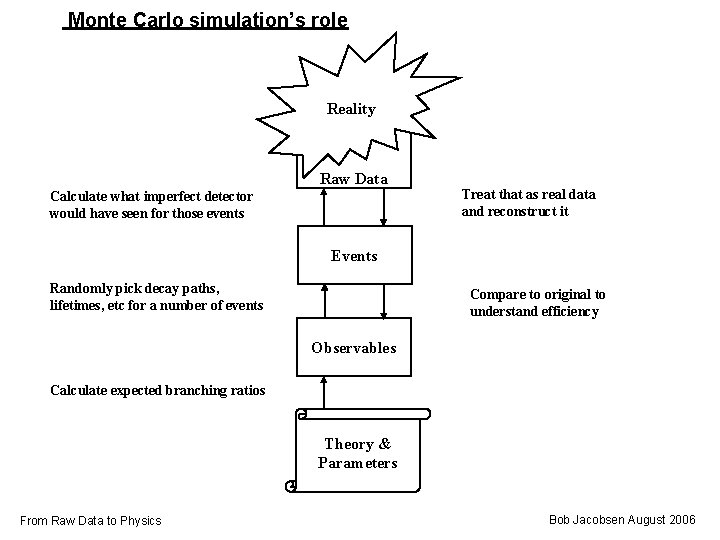
Monte Carlo simulation’s role Reality Raw Data Calculate what imperfect detector would have seen for those events Treat that as real data and reconstruct it Events Randomly pick decay paths, lifetimes, etc for a number of events Compare to original to understand efficiency Observables Calculate expected branching ratios Theory & Parameters From Raw Data to Physics Bob Jacobsen August 2006

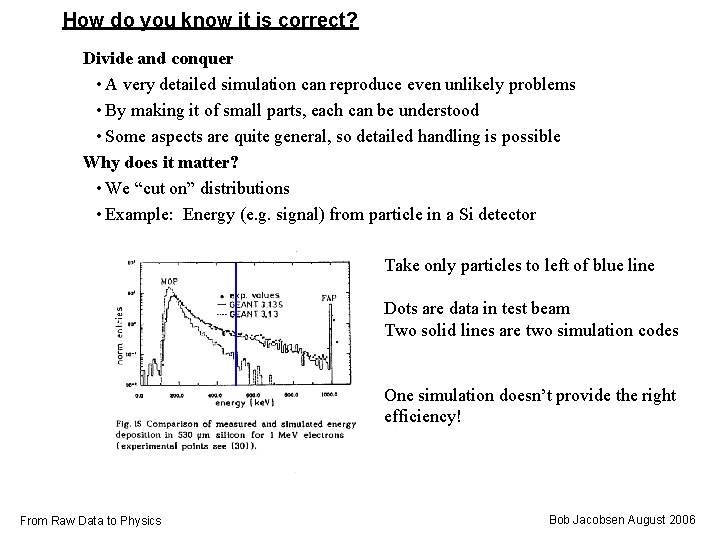
How do you know it is correct? Divide and conquer • A very detailed simulation can reproduce even unlikely problems • By making it of small parts, each can be understood • Some aspects are quite general, so detailed handling is possible Why does it matter? • We “cut on” distributions • Example: Energy (e. g. signal) from particle in a Si detector Take only particles to left of blue line Dots are data in test beam Two solid lines are two simulation codes One simulation doesn’t provide the right efficiency! From Raw Data to Physics Bob Jacobsen August 2006

The tricky part is understanding the discrepancies…. From Raw Data to Physics Bob Jacobsen August 2006

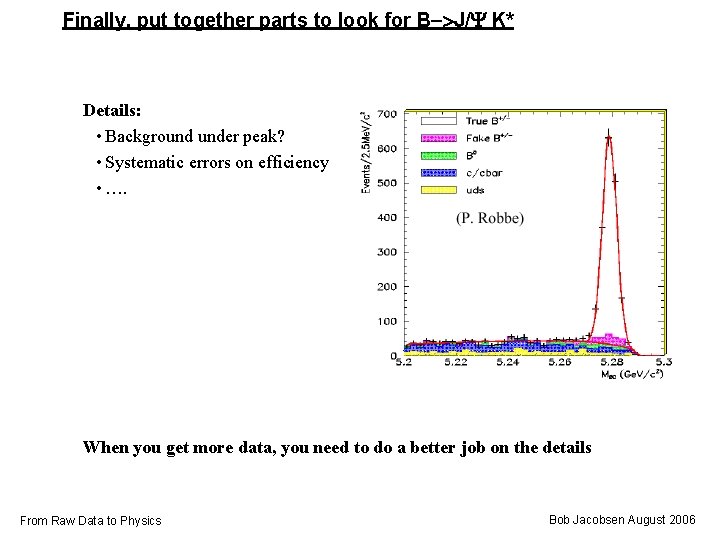
Finally, put together parts to look for B->J/Y K* Details: • Background under peak? • Systematic errors on efficiency • …. When you get more data, you need to do a better job on the details From Raw Data to Physics Bob Jacobsen August 2006

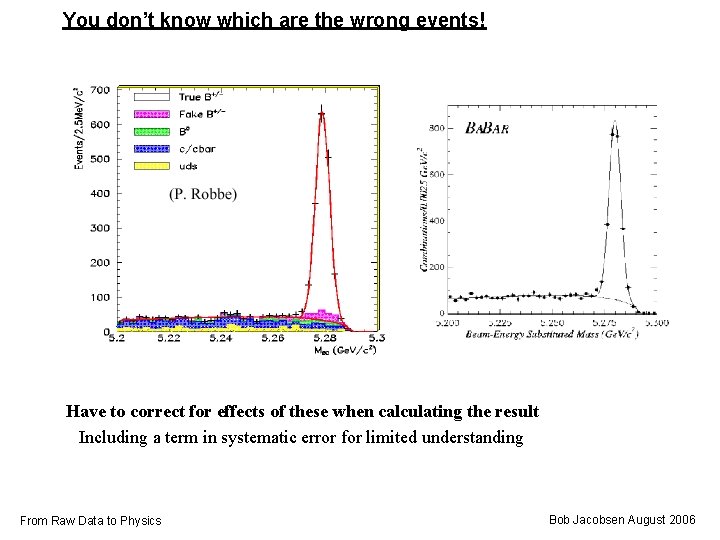
You don’t know which are the wrong events! Have to correct for effects of these when calculating the result Including a term in systematic error for limited understanding From Raw Data to Physics Bob Jacobsen August 2006

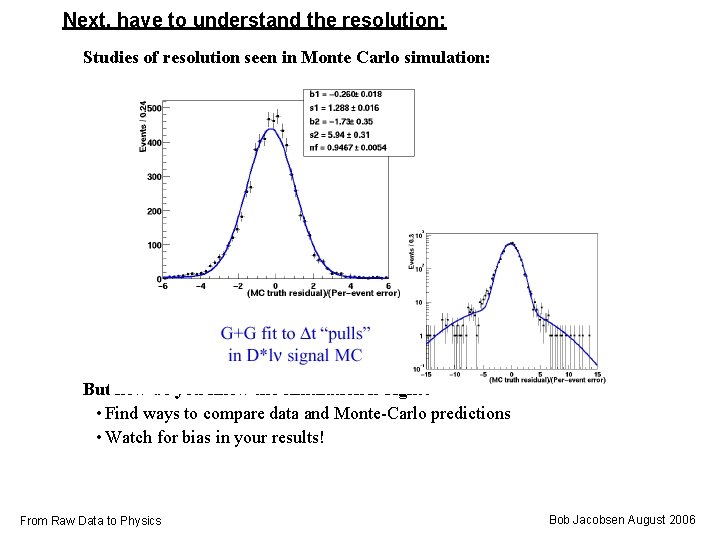
Next, have to understand the resolution: Studies of resolution seen in Monte Carlo simulation: But how do you know the simulation is right? • Find ways to compare data and Monte-Carlo predictions • Watch for bias in your results! From Raw Data to Physics Bob Jacobsen August 2006

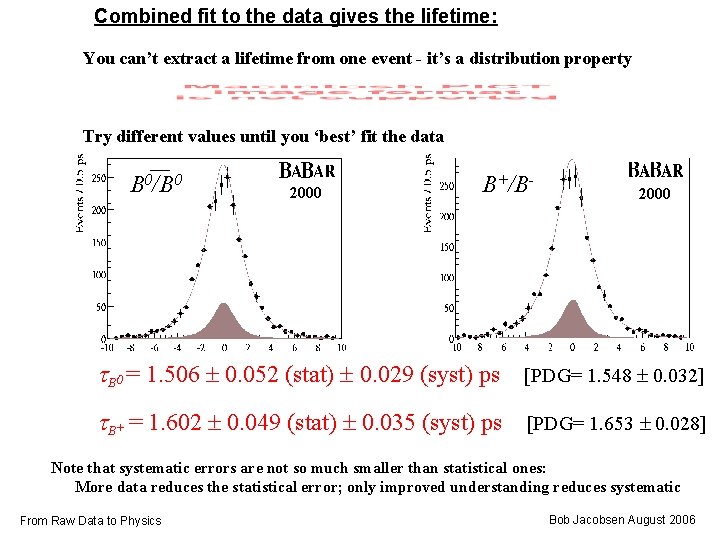
Combined fit to the data gives the lifetime: You can’t extract a lifetime from one event - it’s a distribution property Try different values until you ‘best’ fit the data B 0/B 0 2000 B+/B- 2000 B 0 = 1. 506 0. 052 (stat) 0. 029 (syst) ps [PDG= 1. 548 0. 032] + = 1. 602 0. 049 (stat) 0. 035 (syst) ps [PDG= 1. 653 0. 028] B Note that systematic errors are not so much smaller than statistical ones: More data reduces the statistical error; only improved understanding reduces systematic From Raw Data to Physics Bob Jacobsen August 2006

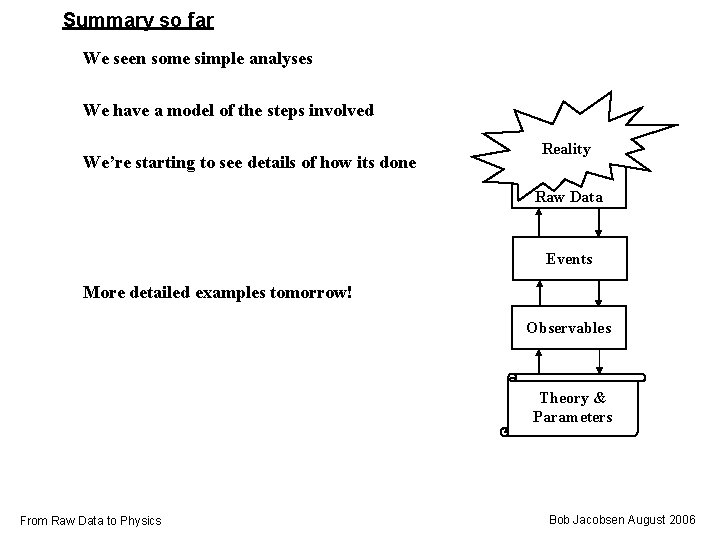
Summary so far We seen some simple analyses We have a model of the steps involved We’re starting to see details of how its done Reality Raw Data Events More detailed examples tomorrow! Observables Theory & Parameters From Raw Data to Physics Bob Jacobsen August 2006