From Modeling in Mathematics Education to the Discovery

From Modeling in Mathematics Education to the Discovery of New Mathematical Knowledge Sergei Abramovich SUNY Potsdam, USA Gennady A. Leonov St Petersburg State University, RUSSIA

Abstract This paper highlights the potential of modeling with spreadsheets and computer algebra systems for the discovery of new mathematical knowledge. Reflecting on work done with prospective secondary teachers in a capstone course, the paper demonstrates the didactic significance of the joint use of experiment and theory in exploring mathematical ideas.

Conference Board of the Mathematical Sciences. 2001. The Mathematical Education of Teachers. Washington, D. C. : MAA. Mathematics Curriculum and Instruction for Prospective Teachers. Recommendation 1. Prospective teachers need mathematics courses that develop deep understanding of mathematics they will teach (p. 7).

Hidden mathematics curriculum s A didactic space for the learning of mathematics where seemingly unrelated concepts emerge to become intrinsically connected by a common thread. s Computational modeling techniques allow for the development of entries into this space for prospective teachers of mathematics

Fibonacci numbers s 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, … Ø Fk+1 = Fk + Fk-1, F 1 = F 2 = 1 • 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, … v 1, 2, 5, 13, 34, 89, … Ø fk+1 = 3 fk - fk-1, f 1 =1, f 2 = 2 q PARAMETERIZATION OF FIBONACCI RECURSION

Ø Two-parametric difference equation Oscar Perron (1954) q THE GOLDEN RATIO

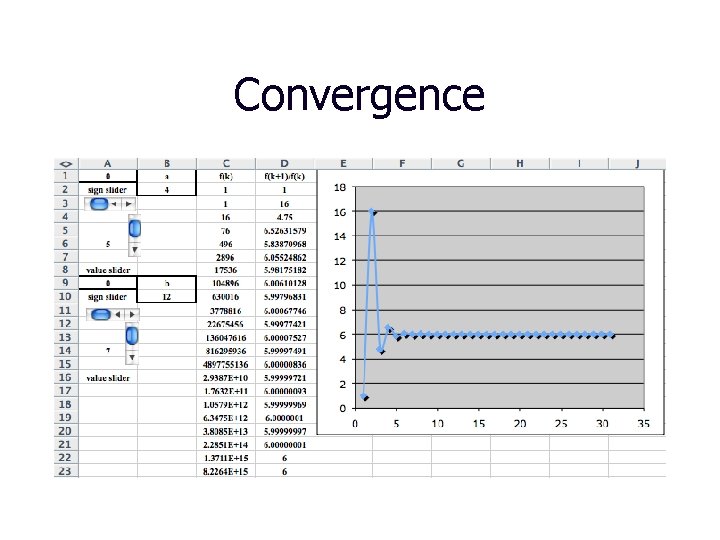
Spreadsheet explorations s How do the ratios fk+1/fk behave as k increases? v Do these ratios converge to a certain number for all values of a and b? Ø How does this number depend on a and b? Generalized Golden Ratio:

Convergence

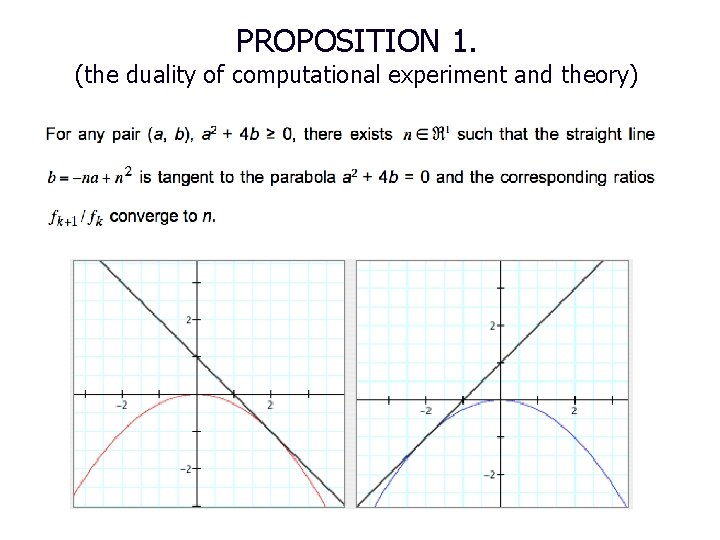
PROPOSITION 1. (the duality of computational experiment and theory) CC

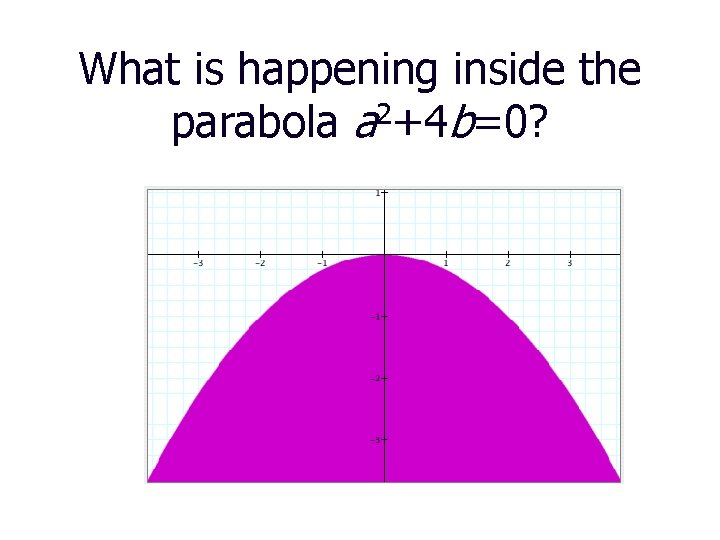
What is happening inside the 2 parabola a +4 b=0?

Hitting upon a cycle of period three {1, -2, 4, …}

Computational Experiment s a 2+b=0 - cycles of period three formed by fk+1/fk (e. g. , a=2, b=-4) s a 2+2 b=0 - cycles of period four formed by fk+1/fk (e. g. , a=2, b=-2) s a 2+3 b=0 - cycles of period six formed by fk+1/fk (e. g. , a=3, b=-3)

Traditionally difficult questions in mathematics research Do there exist cycles with prime number periods? How could those cycles be computed?

Transition to a non-linear equation Continued fractions emerge

Factorable equations of loci (Maple explorations)

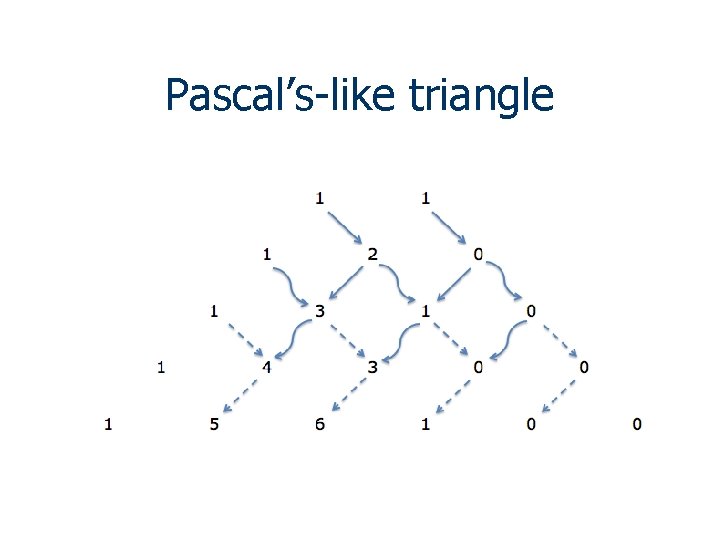
Pascal’s-like triangle

The joint use of Maple and theory

The joint use of Maple and theory

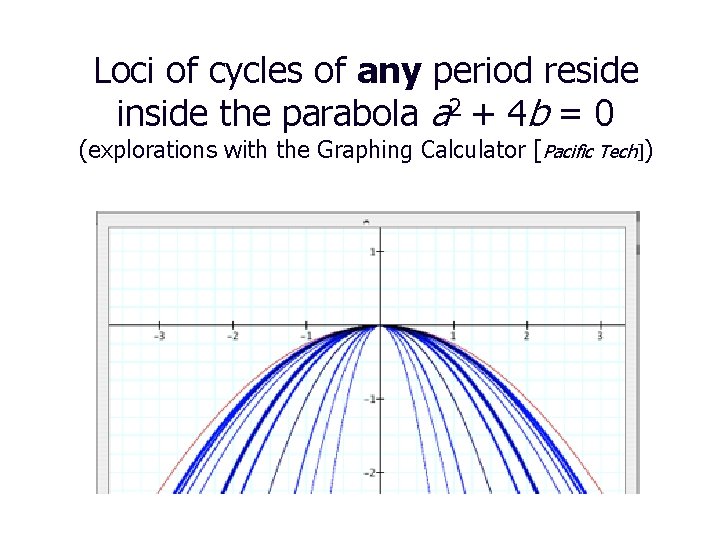
Loci of cycles of any period reside inside the parabola a 2 + 4 b = 0 (explorations with the Graphing Calculator [Pacific Tech])

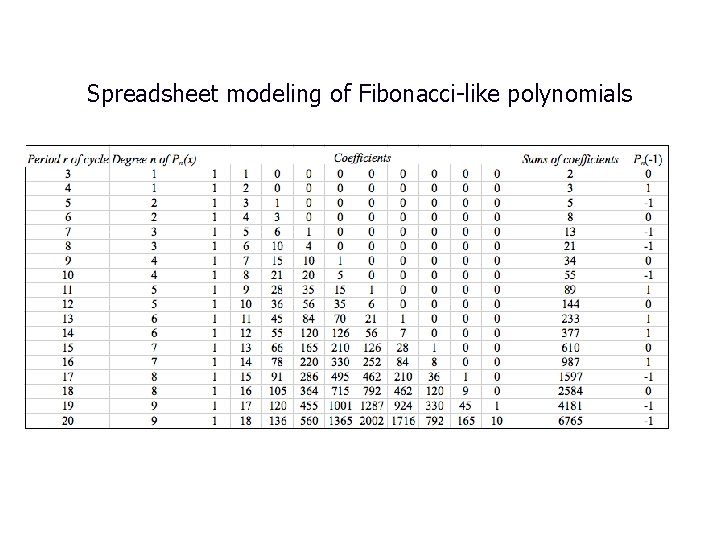
Fibonacci-like polynomials

Spreadsheet modeling of Fibonacci-like polynomials

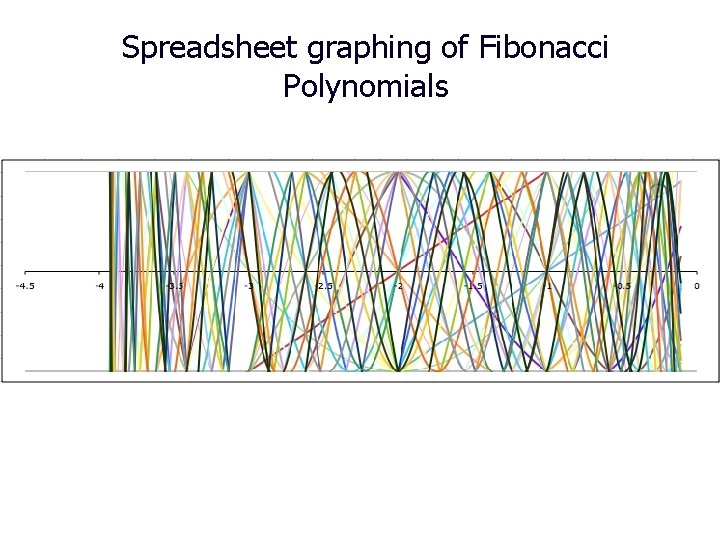
Spreadsheet graphing of Fibonacci Polynomials

Proposition 2. The number of parabolas of the form a 2=msb where the cycles of period r in equation realize, coincides with the number of roots of when n=(r-1)/2 or when n=(r-2)/2.

Proposition 2 a. s Every Fibonacci-like polynomial of degree n has exactly n different roots, all of which are located in the interval (-4, 0).

Proposition 3. For any integer K > 0 there exists integer r > K so that Generalized Golden Ratios oscillate with period r.

Proposition 4 (Maple-based MIP). Corollary (Cassini’s identity):

Permutations with rises. Direction of the cycle on a segment The permutation has exactly n rises on {1, 2, 3, …, p} if there exists exactly n – 1 values of j such that ij < ij+1. Example: [1, 2, 3, …, n] – permutation with n rises The permutation describes the cycle.

Proposition 5. In a p-cycle determined by the largest in absolute value root of Pp-2(x) there always one permutation with two rises, one permutation with p rises, and p-2 permutations with p-1 rises.

Abramovich, S. & Leonov, G. A. (2008). Fibonacci numbers revisited: Technology-motivated inquiry into a two-parametric difference equation. International Journal of Mathematical Education in Science and Technology, 39(6), 749 -766. Abramovich, S. & Leonov, G. A. (2009). Fibonaccilike polynomials: Computational experiments, proofs, and conjectures. International Journal of Pure and Applied Mathematics, 53(4), 489 -496.

Classic example of developing new mathematical knowledge in the context of education Aleksandr Lyapunov (1857 -1918) Central Limit Theorem - the unofficial sovereign of probability theory – was formulated and proved (1901) in the most general form (allowing random variables to exhibit different distributions) as Lyapunov was preparing a new course for students of University of St. Petersburg. Each day try to teach something that you did not know the day before.

Concluding remarks s The potential of modeling in mathematics education as a means of discovery new knowledge. s The interplay of classic and modern ideas s The duality of modeling experiment and theory in exploring mathematical concepts s Appropriate topics for the capstone sequence.