From Graphs to Tables The Design of Scalable

From Graphs to Tables: The Design of Scalable Systems for Graph Analytics Joseph E. Gonzalez Post-doc, UC Berkeley AMPLab jegonzal@eecs. berkeley. edu Co-founder, Graph. Lab Inc. joseph@graphlab. com WWW’ 14 Workshop on Big Graph Mining *These slides are best viewed in Power. Point with anima

Graphs are Central to Analytics Hyperlinks Raw Wikipedia <</ />> </> XML Page. Rank Top 20 Page Title PR Text Table Title Body Term-Doc Topic Model Graph (LDA) Word Topics Word Topic Discussion Table User Disc. Community User Editor Graph Detection Community User Community Topic Com.

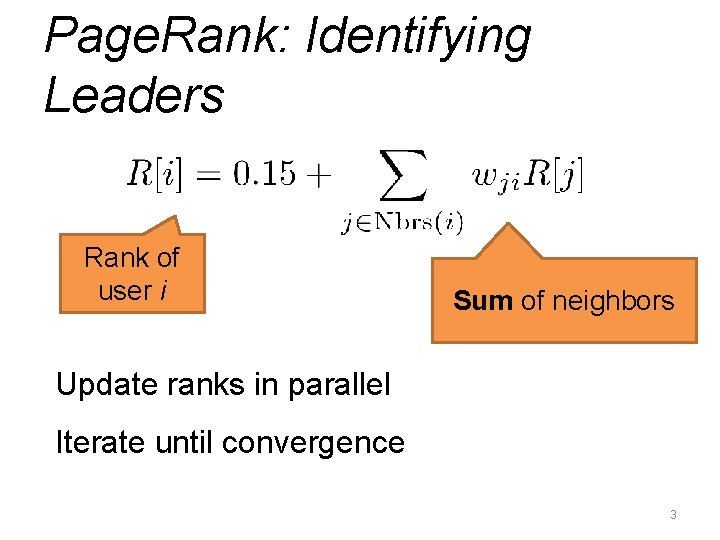
Page. Rank: Identifying Leaders Rank of user i Sum of neighbors Update ranks in parallel Iterate until convergence 3

Recommending Products Users Ratings Item s

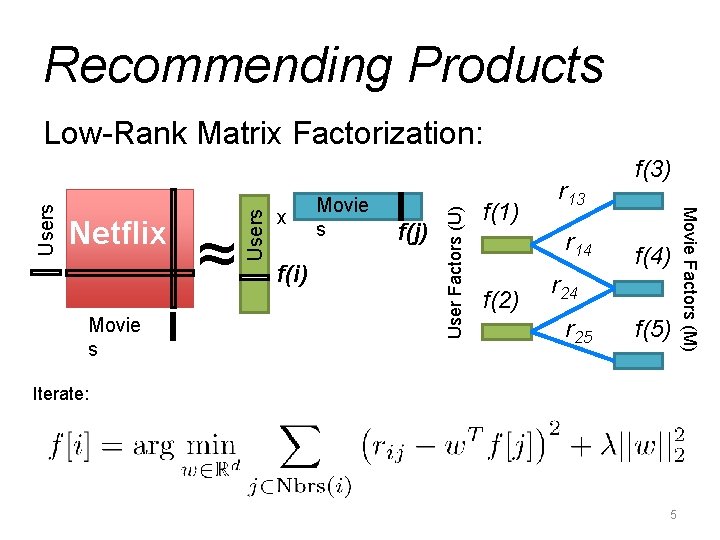
Recommending Products f(i) Movie s f(j) User Factors (U) Movie s ≈ Users Netflix x f(1) r 13 r 14 f(2) f(3) f(4) r 24 r 25 f(5) Iterate: 5 Movie Factors (M) Users Low-Rank Matrix Factorization:

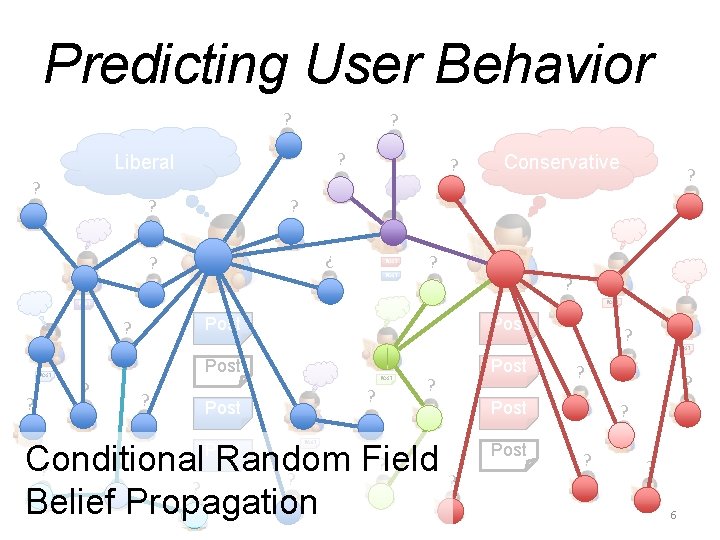
Predicting User Behavior ? ? ? Liberal ? ? ? Conservative ? ? ? Post ? ? Post ? Post ? ? ? Post ? ? Conditional Random Field ? ? ? Belief Propagation Post ? ? Post ? ? ? ? 6

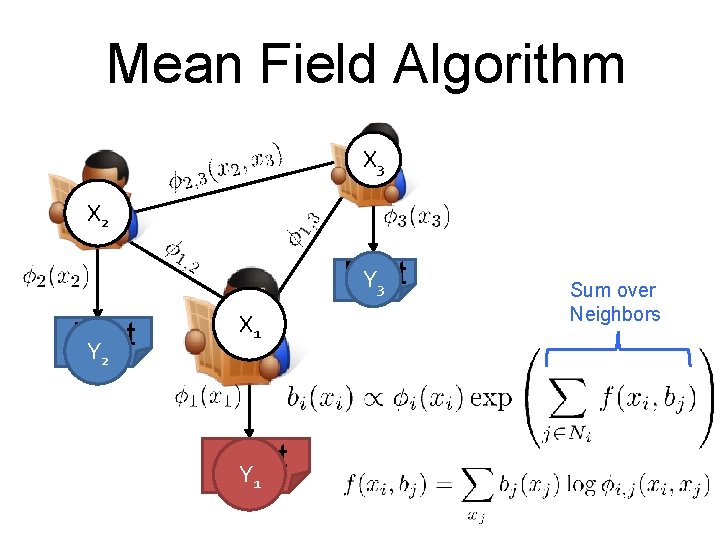
Mean Field Algorithm X 3 X 2 Post Y 3 Post Y X 1 2 Post Y 1 Sum over Neighbors

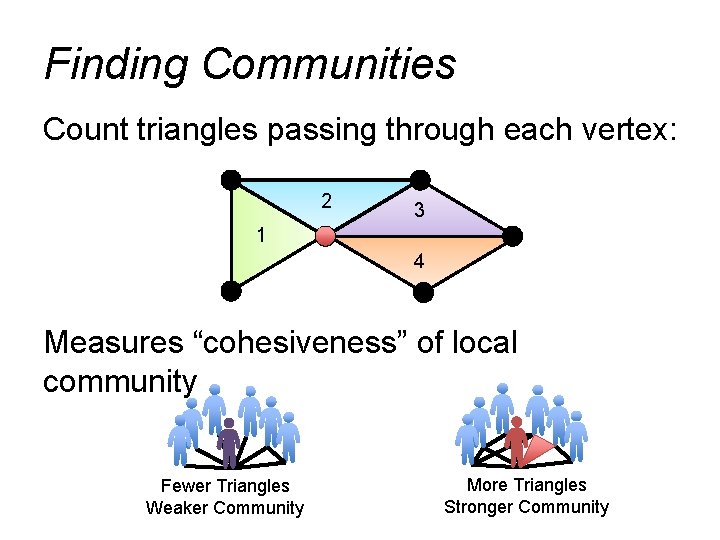
Finding Communities Count triangles passing through each vertex: 2 3 1 4 Measures “cohesiveness” of local community Fewer Triangles Weaker Community More Triangles Stronger Community

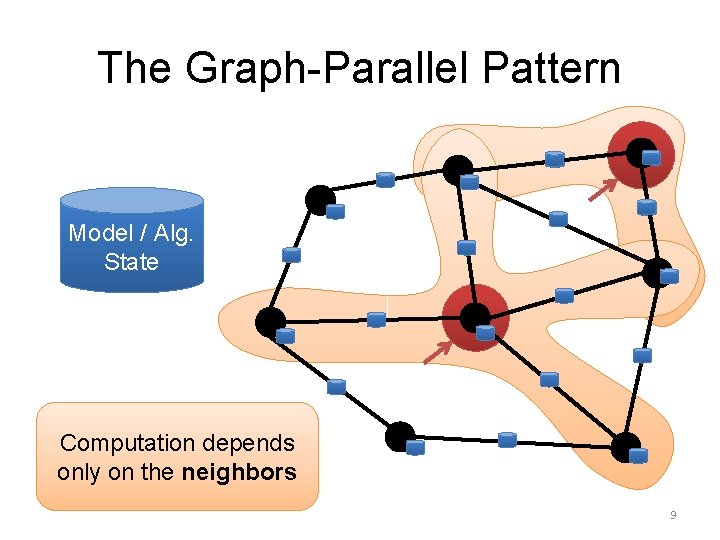
The Graph-Parallel Pattern Model / Alg. State Computation depends only on the neighbors 9

Many Graph-Parallel Algorithms • Collaborative Filtering – Co. EM – Alternating Least Squares • Community Detection – Stochastic Gradient – Triangle-Counting Descent – K-core Decomposition – Tensor Factorization – K-Truss • Structured Prediction – Loopy Belief Propagation – Max-Product Linear Programs – Gibbs Sampling • Semi-supervised ML – Graph SSL • Graph Analytics – – Page. Rank Personalized Page. Rank Shortest Path Graph Coloring • Classification – Neural Networks 10

Graph-Parallel Systems Pregel Expose specialized APIs to simplify graph programming. 11

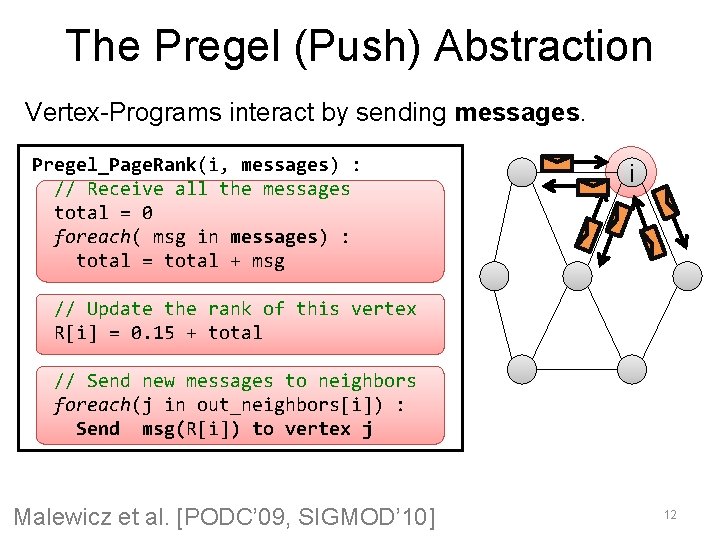
The Pregel (Push) Abstraction Vertex-Programs interact by sending messages. Pregel_Page. Rank(i, messages) : // Receive all the messages total = 0 foreach( msg in messages) : total = total + msg i // Update the rank of this vertex R[i] = 0. 15 + total // Send new messages to neighbors foreach(j in out_neighbors[i]) : Send msg(R[i]) to vertex j Malewicz et al. [PODC’ 09, SIGMOD’ 10] 12

The Graph. Lab (Pull) Abstraction Vertex Programs directly access adjacent vertices and edges ]*w + w 21 3 1 ]* // Update the Page. Rank R[i] = 0. 15 + total + R[3 4 31 R[4] * w 41 R[2 Graph. Lab_Page. Rank(i) // Compute sum over neighbors total = 0 foreach( j in neighbors(i)): total = total + R[j] * wji 2 Data movement is managed by the system and not the user. 13

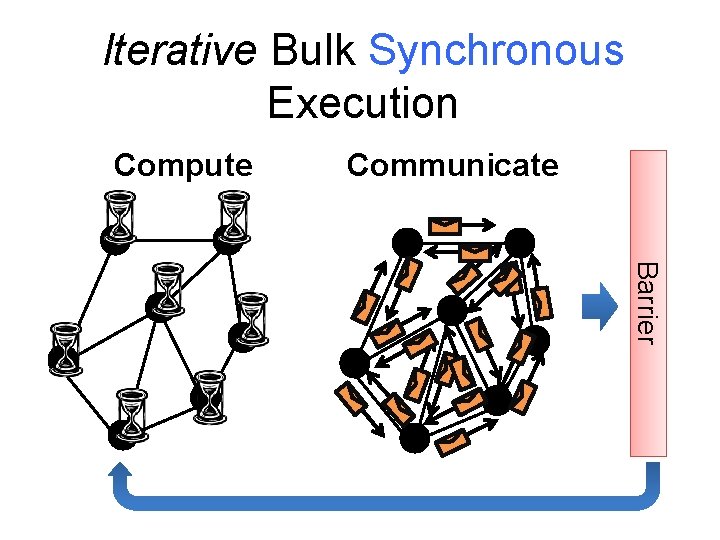
Iterative Bulk Synchronous Execution Compute Communicate Barrier

Graph-Parallel Systems Pregel Exploit graph structure to achieve orders-of-magnitude performance gains over more general data-parallel systems. 15

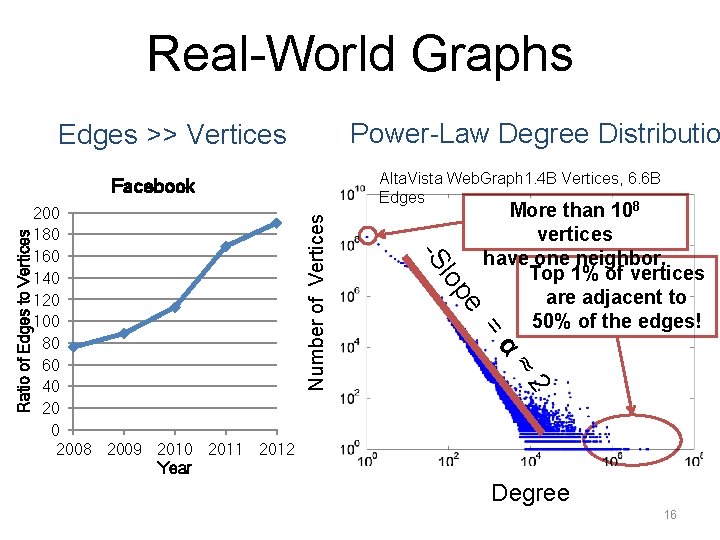
Real-World Graphs Power-Law Degree Distributio Edges >> Vertices Alta. Vista Web. Graph 1. 4 B Vertices, 6. 6 B Edges 8 = α ≈ 2 Number of Vertices More than 10 vertices have one neighbor. Top 1% of vertices are adjacent to 50% of the edges! e 200 180 160 140 120 100 80 60 40 2008 2009 2010 2011 2012 Year lop -S Ratio of Edges to Vertices Facebook Degree 16

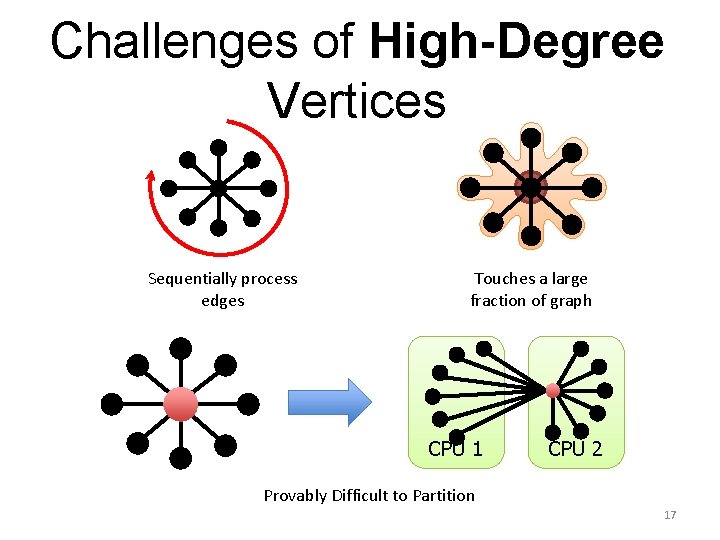
Challenges of High-Degree Vertices Sequentially process edges Touches a large fraction of graph CPU 1 CPU 2 Provably Difficult to Partition 17

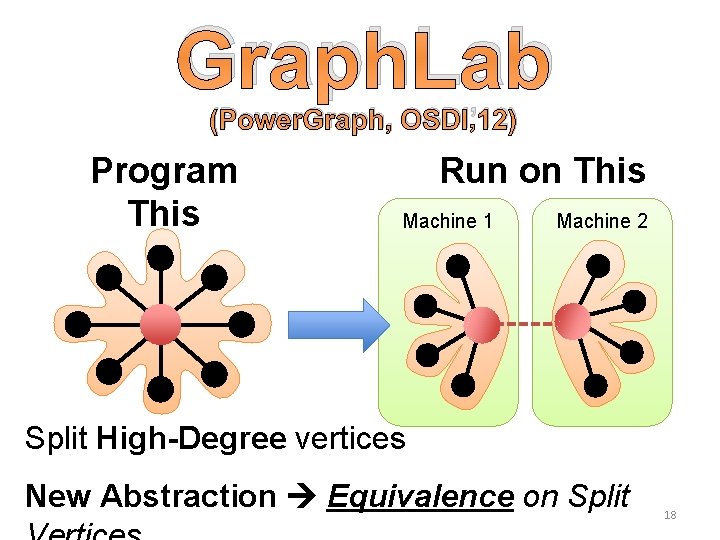
Graph. Lab (Power. Graph, OSDI’ 12) Program This Run on This Machine 1 Machine 2 Split High-Degree vertices New Abstraction Equivalence on Split 18

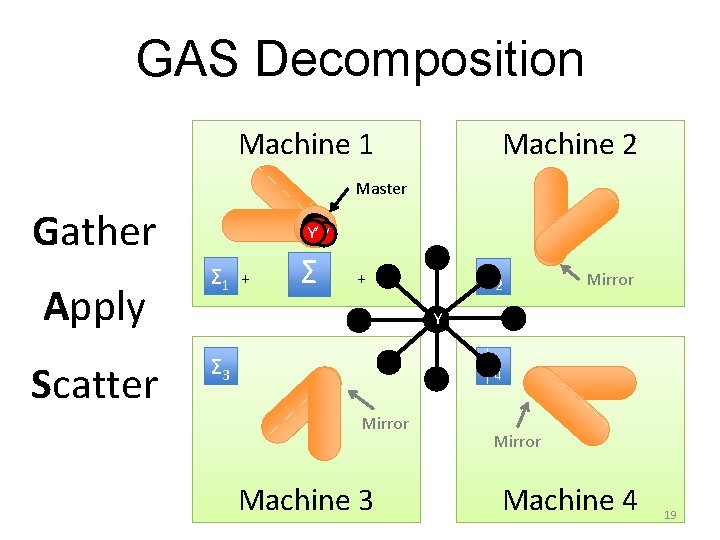
GAS Decomposition Machine 1 Machine 2 Master Gather Apply Scatter Y’ Y’ Σ 1 + Σ 2 + Mirror Y Σ 3 Σ 4 Mirror Machine 3 Mirror Machine 4 19

Minimizing Communication in Power. Graph Y Cut Vertex Communication is linear in the number of machines each vertex spans. Total communication upper bound: 20

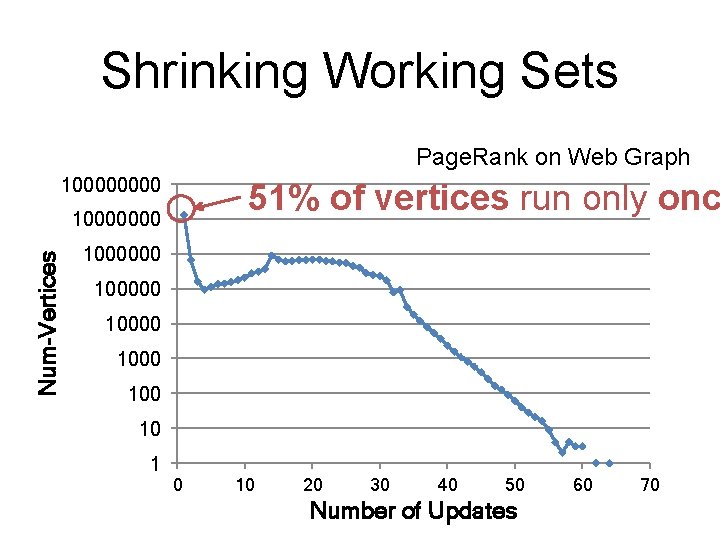
Shrinking Working Sets Page. Rank on Web Graph 10000 51% of vertices run only onc Num-Vertices 10000000 100000 1000 10 1 0 10 20 30 40 50 Number of Updates 60 70

The Graph. Lab (Pull) Abstraction Vertex Programs directly access adjacent vertices and edges 31 1 3 + w 21 ]*w + R[3 4 ]* // Update the Page. Rank R[i] = 0. 15 + total R[4] * w 41 R[2 Graph. Lab_Page. Rank(i) // Compute sum over neighbors total = 0 foreach( j in neighbors(i)): total = total + R[j] * wji 2 // Trigger neighbors to run again if R[i] not converged then signal nbrs. Of(i) to be recomputed Trigger computation only when necessary. 22

Page. Rank on the Live-Journal Graph Mahout/ Hadoop Naïve Spark Graph. La b 1340 354 22 0 200 400 600 800 1000 1200 1400 1600 Runtime (in seconds, Page. Rank for 10 iterations) Graph. Lab is 60 x faster than Hadoop Graph. Lab is 16 x faster than Spark

Triangle Counting on Twitter 40 M Users, 1. 4 Billion Links Counted: 34. 8 Billion Triangles Hadoop [WWW’ 11] Graph. Lab 1536 Machines 423 Minutes 64 Machines 15 Seconds 1000 x Faster 24 S. Suri and S. Vassilvitskii, “Counting triangles and the curse of the last reducer, ” WWW’ 11

Graph Analytics Pipeline Hyperlinks Raw Wikipedia <</ />> </> XML Page. Rank Top 20 Page Title PR Text Table Title Body Term-Doc Topic Model Graph (LDA) Word Topics Word Topic Discussion Table User Disc. Community User Editor Graph Detection Community User Community Topic Com.

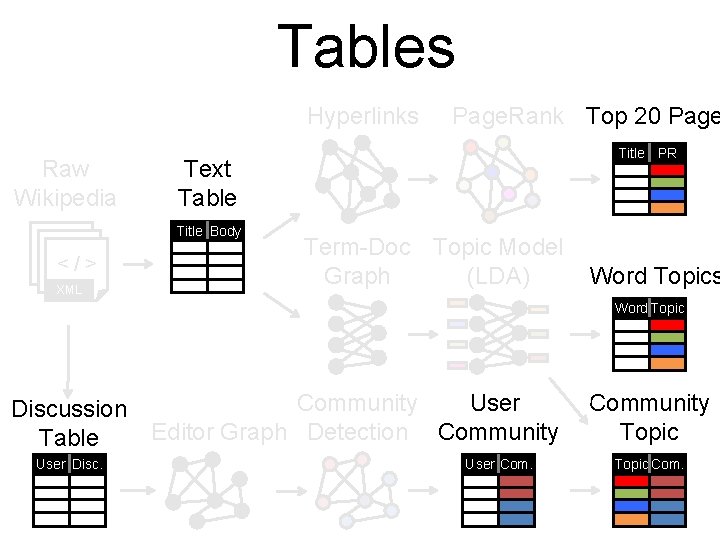
Tables Hyperlinks Raw Wikipedia <</ />> </> XML Page. Rank Top 20 Page Title PR Text Table Title Body Term-Doc Topic Model Graph (LDA) Word Topics Word Topic Discussion Table User Disc. Community User Editor Graph Detection Community User Community Topic Com.

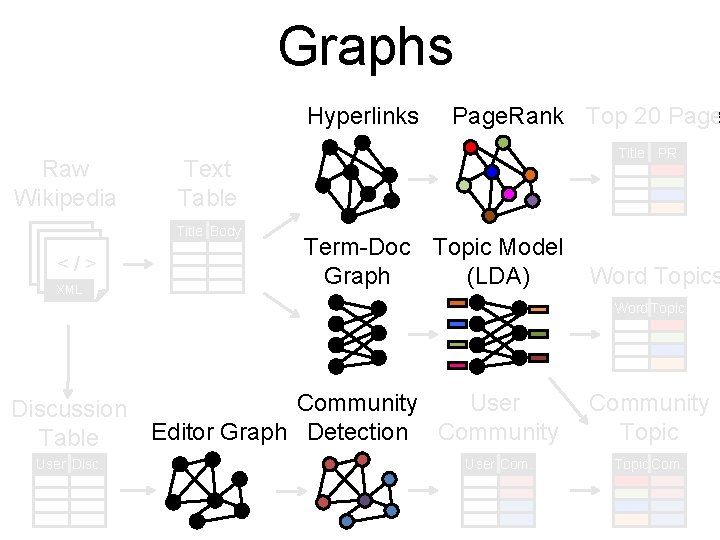
Graphs Hyperlinks Raw Wikipedia <</ />> </> XML Page. Rank Top 20 Page Title PR Text Table Title Body Term-Doc Topic Model Graph (LDA) Word Topics Word Topic Discussion Table User Disc. Community User Editor Graph Detection Community User Community Topic Com.

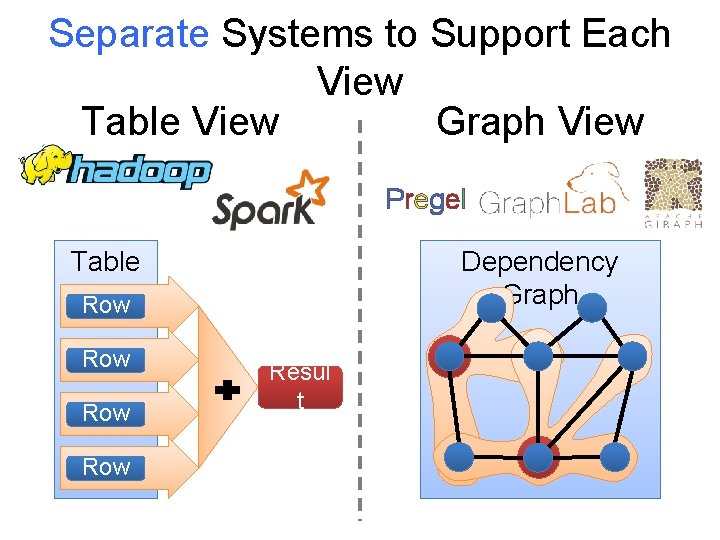
Separate Systems to Support Each View Table View Graph View Pregel Table Dependency Graph Row Row Resul t

Separate systems for each view can be difficult to use and inefficient 29

Difficult to Program and Users must Learn, Deploy, and Manage multiple systems Leads to brittle and often complex interfaces 30

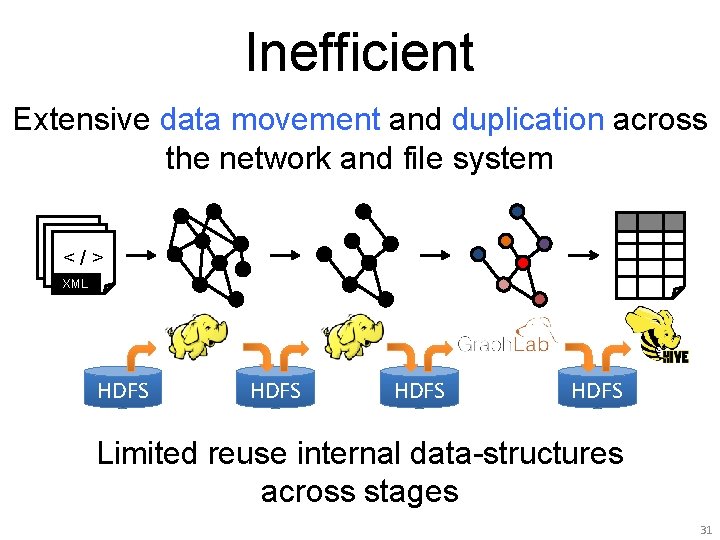
Inefficient Extensive data movement and duplication across the network and file system <</ />> </> XML HDFS Limited reuse internal data-structures across stages 31

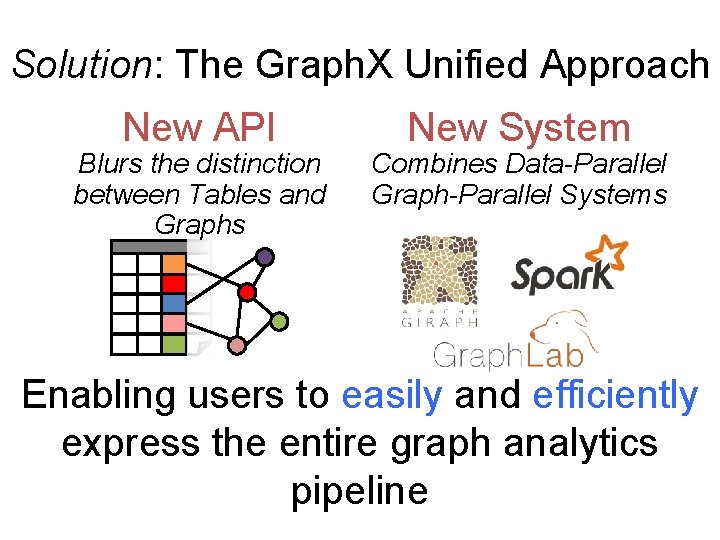
Solution: The Graph. X Unified Approach New API Blurs the distinction between Tables and Graphs New System Combines Data-Parallel Graph-Parallel Systems Enabling users to easily and efficiently express the entire graph analytics pipeline

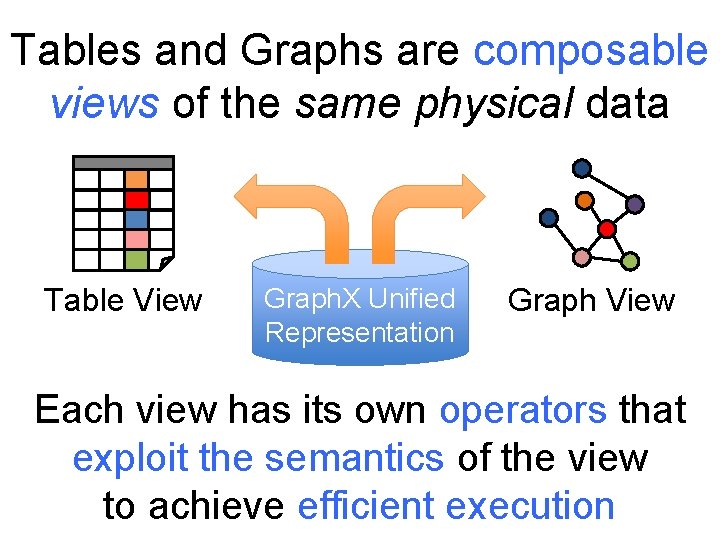
Tables and Graphs are composable views of the same physical data Table View Graph. X Unified Representation Graph View Each view has its own operators that exploit the semantics of the view to achieve efficient execution

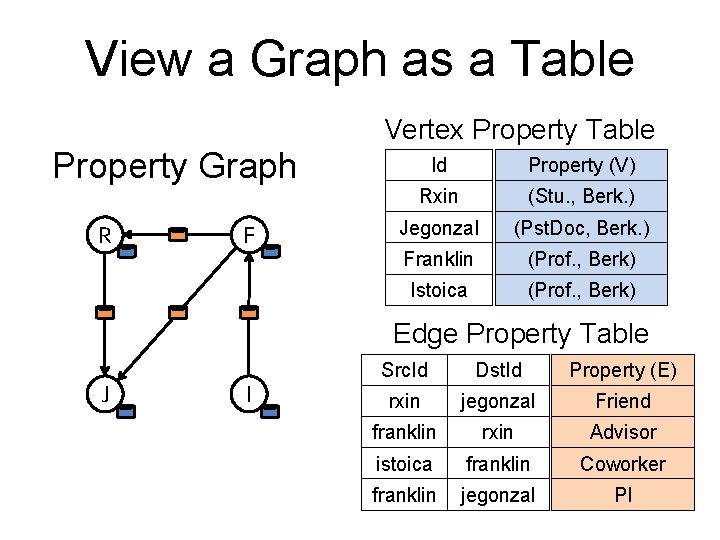
View a Graph as a Table Vertex Property Table Property Graph R F Id Property (V) Rxin (Stu. , Berk. ) Jegonzal (Pst. Doc, Berk. ) Franklin (Prof. , Berk) Istoica (Prof. , Berk) Edge Property Table J I Src. Id Dst. Id Property (E) rxin jegonzal Friend franklin rxin Advisor istoica franklin Coworker franklin jegonzal PI

Table Operators Table (RDD) operators are inherited from Spark: map reduce sample filter count take group. By fold first sort reduce. By. Key partition. By union group. By. Key map. With join cogroup pipe left. Outer. Join cross save right. Outer. Join zip . . . 35

Graph Operators class Graph [ V, E ] { def Graph(vertices: Table[ (Id, V) ], edges: Table[ (Id, E) ]) // Table Views --------def vertices: Table[ (Id, V) ] def edges: Table[ (Id, E) ] def triplets: Table [ ((Id, V), E) ] // Transformations ---------------def reverse: Graph[V, E] def subgraph(p. V: (Id, V) => Boolean, p. E: Edge[V, E] => Boolean): Graph[V, E] def map. V(m: (Id, V) => T ): Graph[T, E] def map. E(m: Edge[V, E] => T ): Graph[V, T] // Joins --------------------def join. V(tbl: Table [(Id, T)]): Graph[(V, T), E ] def join. E(tbl: Table [(Id, T)]): Graph[V, (E, T)] // Computation -----------------def mr. Triplets(map. F: (Edge[V, E]) => List[(Id, T)], reduce. F: (T, T) => T): Graph[T, E] } 36

Triplets Join Vertices and Edges The triplets operator joins vertices and edges: Verticess. Id, d. Id, Triplets SELECT s. P, e. P, d. P Edges A B FROMA edges AS e C JOIN Bvertices AS ASAd A s, vertices C C ON e. src. Id = s. Id. B ANDCe. dst. Id =Bd. Id C D C D The mr. Triplets operator sums adjacent triplets. SELECT t. dst. Id, reduce( map(t) ) AS sum FROM triplets AS t GROUPBY t. dst. Id

We express enhanced Pregel and Graph. Lab abstractions using the Graph. X operators in less than 50 lines of code! 38

Enhanced to Pregel in Graph. X pregel. PR(i, message. List ): message. Sum Require Message Combiners // Receive all the messages total = 0 message. Sum foreach( msg in message. List) : total = total + msg // Update the rank of this vertex R[i] = 0. 15 + total combine. Msg(a, b): // Compute summessages of two messages // Send new to neighbors send. Msg(i j, R[i], R[j], E[i, j]): return a + b in out_neighbors[i]) : foreach(j // Compute single message Send msg(R[i]/E[i, j]) to vertex return msg(R[i]/E[i, j]) Malewicz et al. [PODC’ 09, SIGMOD’ 10] Remove Message Computation from the Vertex Program 39

Implementing Page. Rank in Graph. X // Load and initialize the graph val graph = Graph. Builder. text(“hdfs: //web. txt”) val pr. Graph = graph. join. Vertices(graph. out. Degrees) // Implement and Run Page. Rank val page. Rank = pr. Graph. pregel(initial. Message = 0. 0, iter = 10)( (old. V, msg. Sum) => 0. 15 + 0. 85 * msg. Sum, triplet => triplet. src. pr / triplet. src. deg, (msg. A, msg. B) => msg. A + msg. B) 40

We express the Pregel and Graph. Lab like abstractions using the Graph. X operators in less than 50 lines of code! By composing these operators we can construct entire graph-analytics pipelines. 41

Example Analytics Pipeline // Load raw data tables val verts = sc. text. File(“hdfs: //users. txt”). map(parser. V) val edges = sc. text. File(“hdfs: //follow. txt”). map(parser. E) // Build the graph from tables and restrict to recent links val graph = new Graph(verts, edges) val recent = graph. subgraph(edge => edge. date > LAST_MONTH) // Run Page. Rank Algorithm val pr = graph. Page. Rank(tol = 1. 0 e-5) // Extract and print the top 25 users val top. Users = verts. join(pr). top(25). collect top. Users. foreach(u => println(u. name + ‘t’ + u. pr))

Graph. X System Design

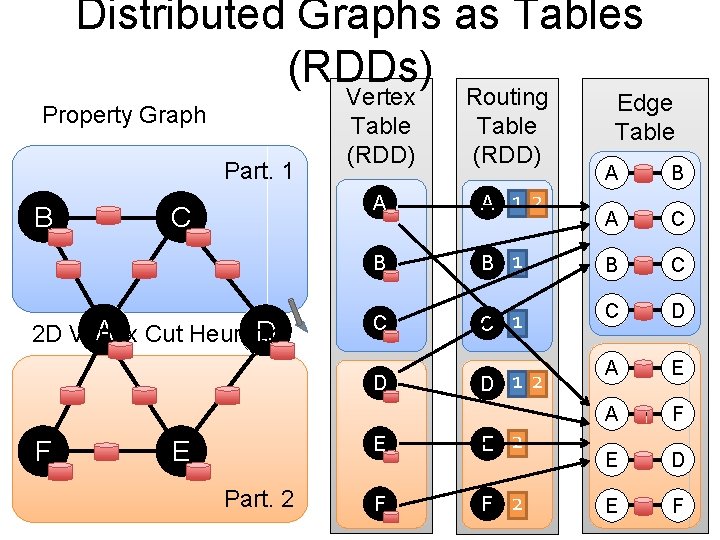
Distributed Graphs as Tables (RDDs) Property Graph Part. 1 B C A D 2 D Vertex A Cut Heuristic D Vertex Table (RDD) A A 12 B B C C D F E Part. 2 Routing Table (RDD) D Edge Table (RDD)B A A C 1 B C 1 C D 12 A E A F E D E F E E 2 F F 2

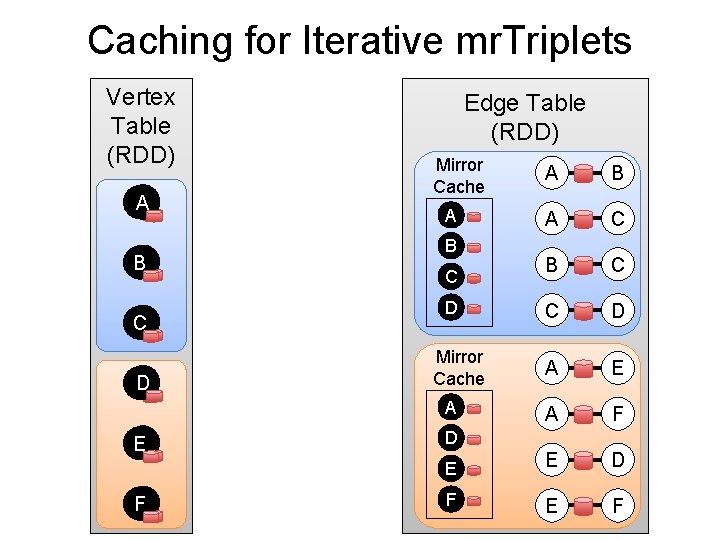
Caching for Iterative mr. Triplets Vertex Table (RDD) A A B B C C D D Edge Table (RDD) Mirror Cache A B A C B C C D A E A F E E D F E F A B C D Mirror Cache A E E FF D

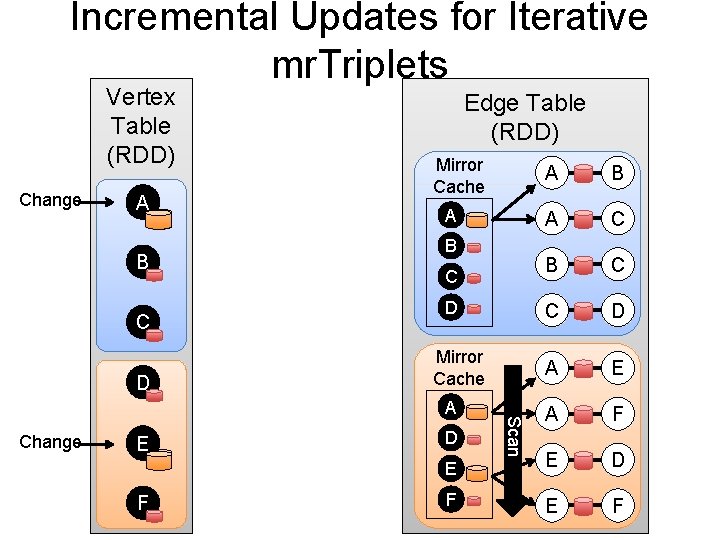
Incremental Updates for Iterative mr. Triplets Vertex Table (RDD) Change A B C D Edge Table (RDD) Mirror Cache A B A C B C C D A E A F E E D F E F A B C D Mirror Cache Change E F D Scan A

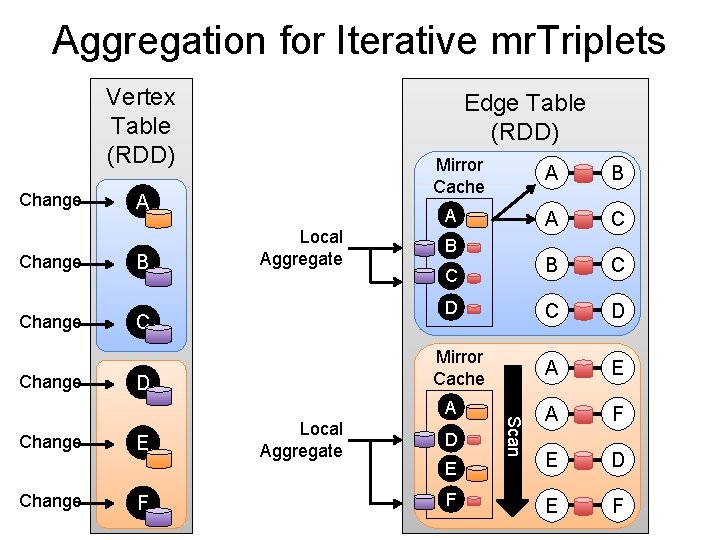
Aggregation for Iterative mr. Triplets Vertex Table (RDD) Change Edge Table (RDD) Mirror Cache A B A C B C C D A E A F E E D F E F A Local Aggregate B C D C Mirror Cache D Change E F Local Aggregate D Scan A

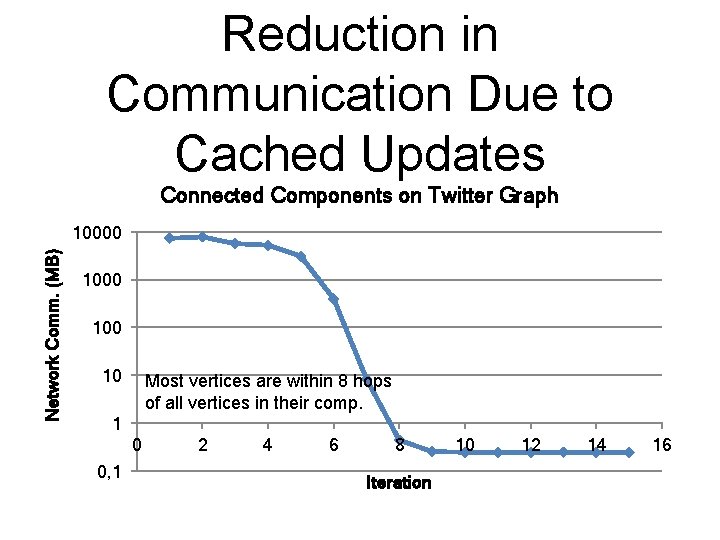
Reduction in Communication Due to Cached Updates Connected Components on Twitter Graph Network Comm. (MB) 10000 100 10 Most vertices are within 8 hops of all vertices in their comp. 1 0 0, 1 2 4 6 8 Iteration 10 12 14 16

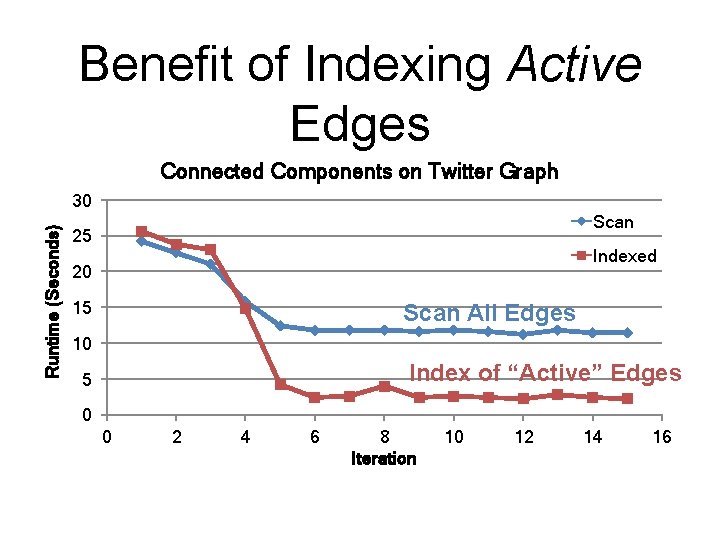
Benefit of Indexing Active Edges Connected Components on Twitter Graph Runtime (Seconds) 30 Scan 25 Indexed 20 15 Scan All Edges 10 Index of “Active” Edges 5 0 0 2 4 6 8 Iteration 10 12 14 16

Join Elimination Identify and bypass joins for unused triplet fields send. Msg(i j, R[i], R[j], E[i, j]): // Compute single message return msg(R[i]/E[i, j]) Communication (MB) Page. Rank on Twitter 14000 12000 10000 8000 6000 4000 2000 0 Three Way Join Elimination Factor of 2 reduction in communication 0 5 10 Iteration 15 20 50

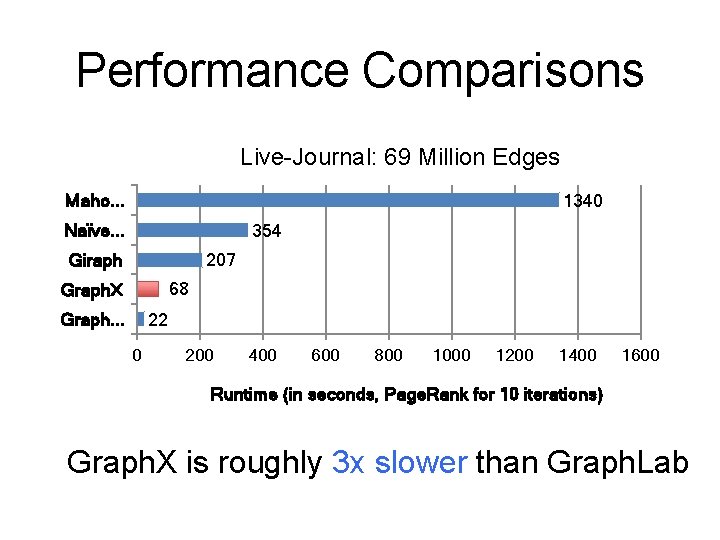
Performance Comparisons Live-Journal: 69 Million Edges Maho. . . 1340 Naïve. . . 354 Giraph 207 68 Graph. X Graph. . . 22 0 200 400 600 800 1000 1200 1400 1600 Runtime (in seconds, Page. Rank for 10 iterations) Graph. X is roughly 3 x slower than Graph. Lab

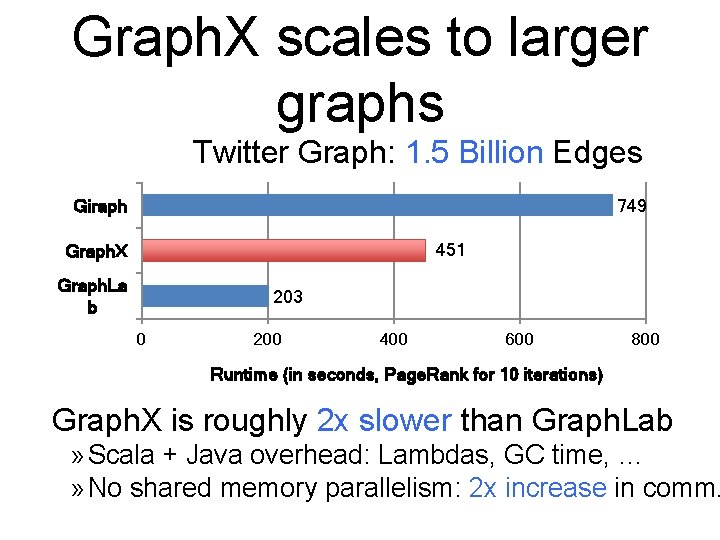
Graph. X scales to larger graphs Twitter Graph: 1. 5 Billion Edges Giraph 749 451 Graph. X Graph. La b 203 0 200 400 600 800 Runtime (in seconds, Page. Rank for 10 iterations) Graph. X is roughly 2 x slower than Graph. Lab » Scala + Java overhead: Lambdas, GC time, … » No shared memory parallelism: 2 x increase in comm.

Page. Rank is just one stage…. What about a pipeline?

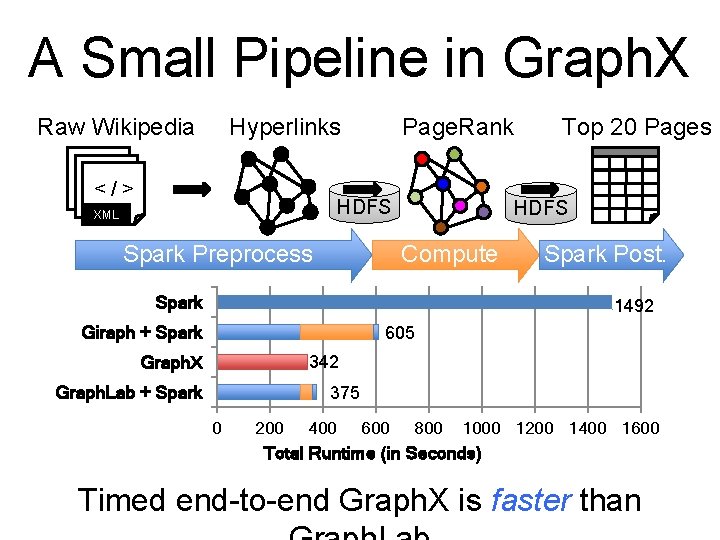
A Small Pipeline in Graph. X Raw Wikipedia Hyperlinks <</ />> </> Page. Rank HDFS XML Spark Preprocess Top 20 Pages HDFS Compute Spark Post. 1492 Giraph + Spark 605 342 Graph. X Graph. Lab + Spark 375 0 200 400 600 800 1000 1200 1400 1600 Total Runtime (in Seconds) Timed end-to-end Graph. X is faster than

Conclusion and Observations Domain specific views: Tables and Graphs » tables and graphs are first-class composable objects » specialized operators which exploit view semantics Single system that efficiently spans the pipeline » minimize data movement and duplication » eliminates need to learn and manage multiple systems Graphs through the lens of database 56

Open Source Project Alpha release as part of Spark 0. 9

Active Research Static Data Dynamic Data » Apply Graph. X unified approach to time evolving data » Materialized view maintenance for graphs Serving Graph Structured Data » Allow external systems to interact with Graph. X » Unify distributed graph databases with relational database technology 58

Collaborators Graph. Lab: Yucheng Haijie Low Gu Aapo Danny Carlos Alex Kyrola Bickson Guestrin Smola Guy Blelloch Graph. X: Reynold Xin Ankur Dave Daniel Crankshaw Michael Franklin Ion Stoica

Thanks! http: //tinyurl. com/ampgraphx jegonzal@eecs. berkeley. edu