From geometric optics to plants eikonal equation for

From geometric optics to plants: eikonal equation for buckling… and beyond Sergei Nechaev Interdisciplinsary Scientific Center Poncelet (CNRS, Moscow) Lebedev Physical Institute (RAS, Moscow)

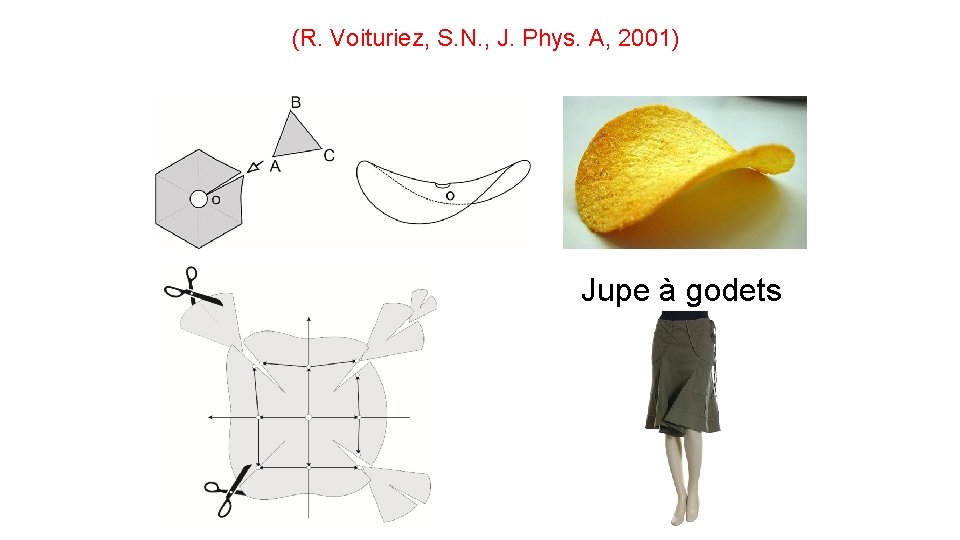
How to describe the profile?

(R. Voituriez, S. N. , J. Phys. A, 2001) Jupe à godets

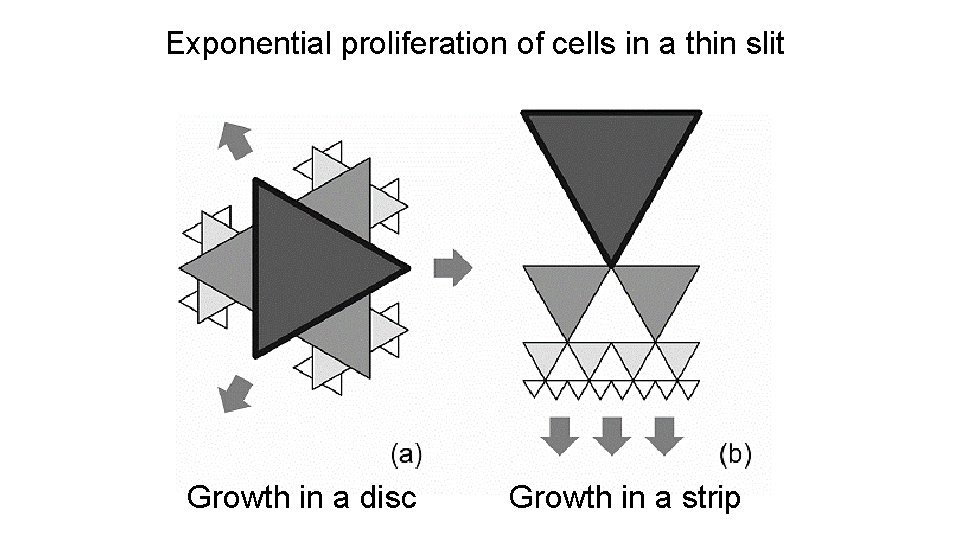
Exponential proliferation of cells in a thin slit Growth in a disc Growth in a strip

When we open the slit, the material relaxes into the 3 D structure Conjecture: buckling occurs as a conflict between internal geometry of object and geometry of space of embedding

Growth induces an increasing strain in a tissue near its edge and results in: (i) in-plane tissue compression and/or redistribution of layer cells accompanied by the in-plane circumference instability (“stretching”) (ii) out-of-plane tissue buckling with the formation of saddle-like surface regions (“bending”) Energetic approach to growing patterns is based on a competition between the bending and stretching energies of elastic membranes For bending rigidity of a thin membrane B ~ h 3, while for stretching rigidity, S ~ h, where h is the membrane thickness. Thin enough tissues, with h <<1, prefer to bend, i. e. to be negatively curved under relatively small critical strain

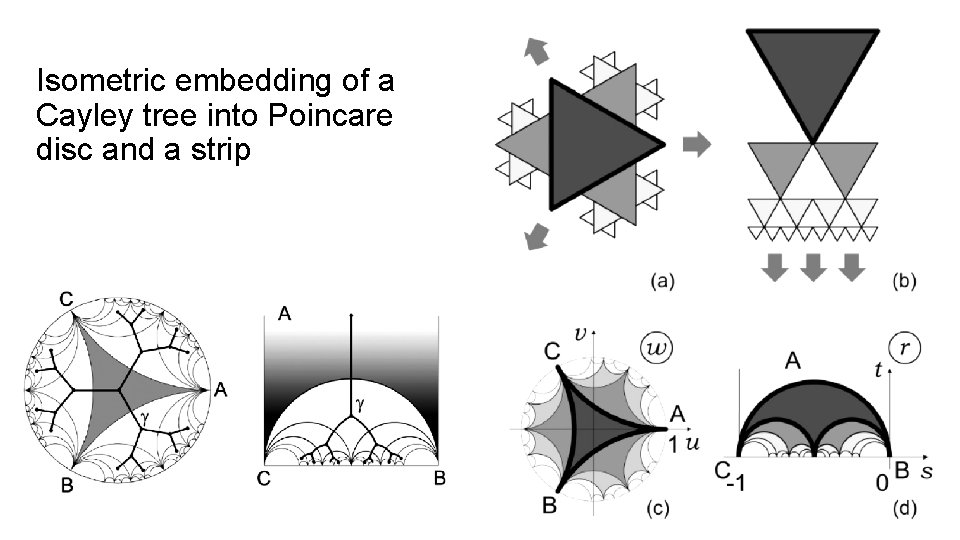
Formulation of the problem Exponentially growing colony, being the hyperbolic structure, admits Cayley trees as possible discretizations. The Cayley trees cover the hyperbolic surface isometrically, i. e. without gaps and selfintersections, preserving angles and distances. Our goal is an embedding a Cayley tree into a 3 D Euclidean space with a signature {+1, +1}. Hilbert theorem prohibits embedding of unbounded Hyperbolic surface into Euclidean space smoothly

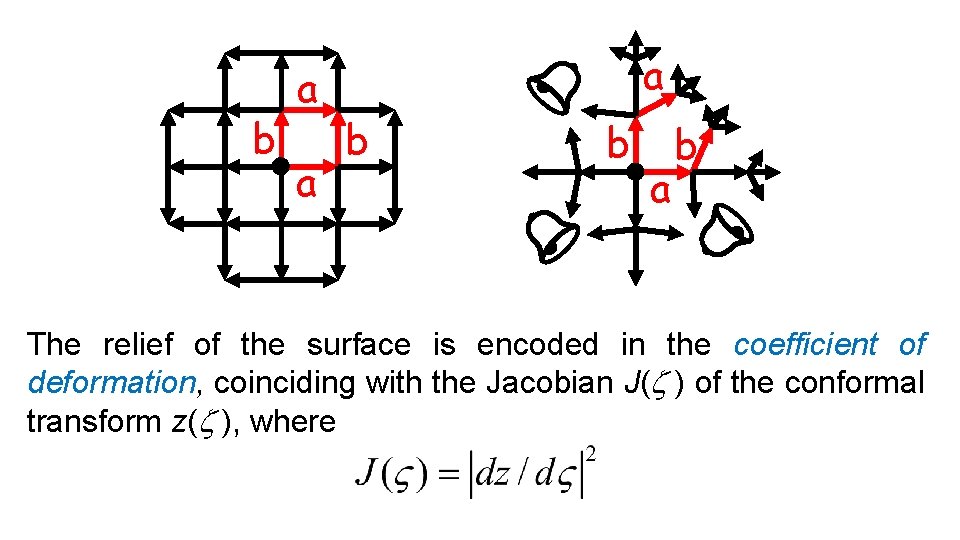
a b a b b a The relief of the surface is encoded in the coefficient of deformation, coinciding with the Jacobian J(z ) of the conformal transform z(z ), where

Isometric embedding of a Cayley tree into Poincare disc and a strip

Optimal profile – is the surface in which we can embed the exponentially growing graph isometrically (S. N. , K. Polovnikov, Soft Matter, 2017) The metric ds 2 of a 2 D surface parametrized by (u, v), is given by the coefficients G F of the first quadratic form of this surface The surface area then reads

Surface embedded in 3 D has the same metric as Poincare disc If z(w) is holomorphic, the Cauchy-Riemann conditions provide

Surface embedded in 3 D has the same metric as Poincare disc If we impose the condition for a surface to be a function above (u, v), then we could write the surface element in curvilinear coordinates

Relief of the surface f (u, v) is defined by the eikonal equation In our particular case we have to solve the following equation for the function f (u, v) a-2 where is the Dedekind h-function

Geometric optic analogy a-2

Fermat principle Time dt for a ray propagating along g between points M(x) and N(x+dx) should be minimal where is the refraction coefficient and c and v(x) are the light speed in vacuum and in the medium, d|x| = ds is the spatial increment along the ray. Supposing that the “optic length”, S=c. T, is the action, we have with the Lagrangian Minimizing the action. Due to Huygens principle , we get the equation we find

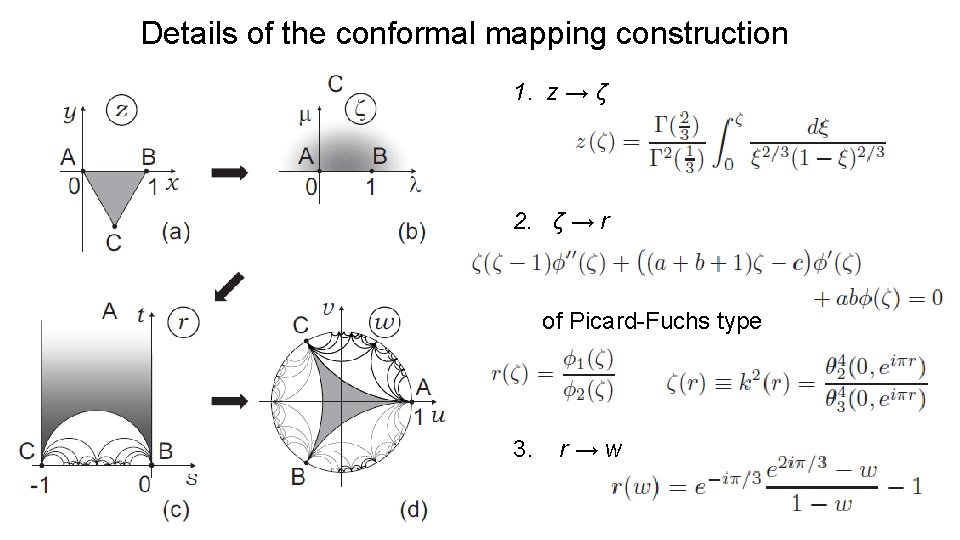
Details of the conformal mapping construction 1. z → ζ 2. ζ → r of Picard-Fuchs type 3. r→w

Solution of the eikonal equation 1) In polar coordinates (for a disc): and 2) In rectangular coordinates (for a strip): and where

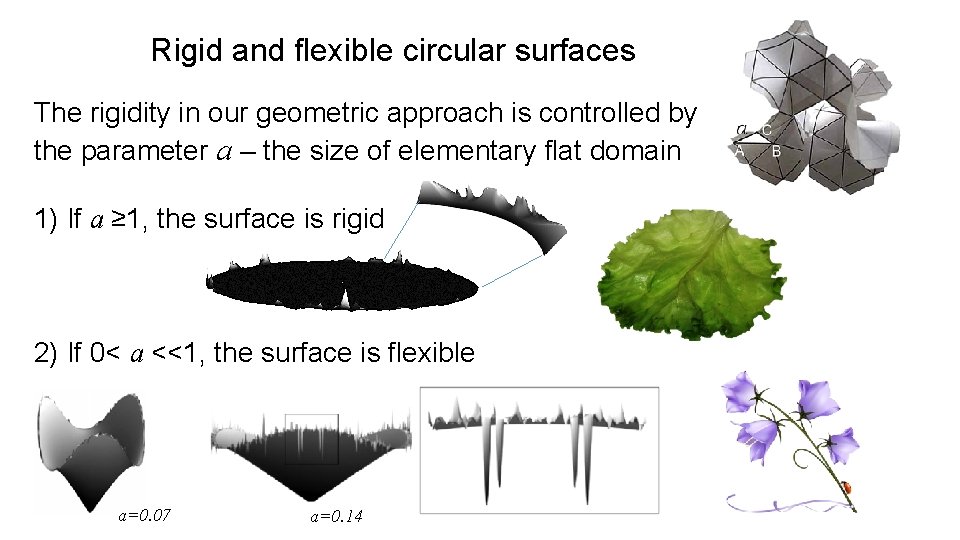
Rigid and flexible circular surfaces The rigidity in our geometric approach is controlled by the parameter a – the size of elementary flat domain 1) If a ≥ 1, the surface is rigid 2) If 0< a <<1, the surface is flexible a=0. 07 a=0. 14

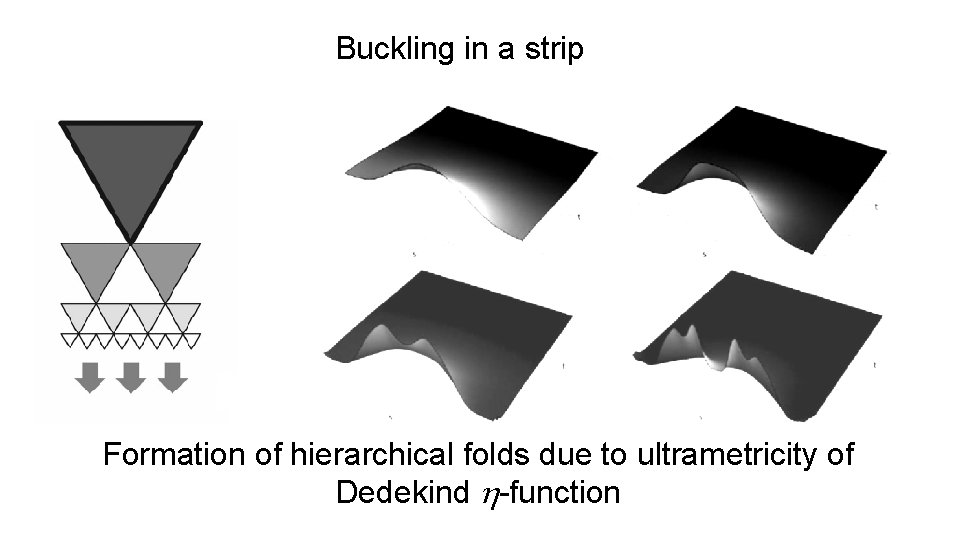
Buckling in a strip Formation of hierarchical folds due to ultrametricity of Dedekind h-function

Speculation: how to interpret the complex-valued refraction index?

“Energetic view” on conformal approach Metric tensor from conformal approach Metric tensor of deformed sample eikonal equation

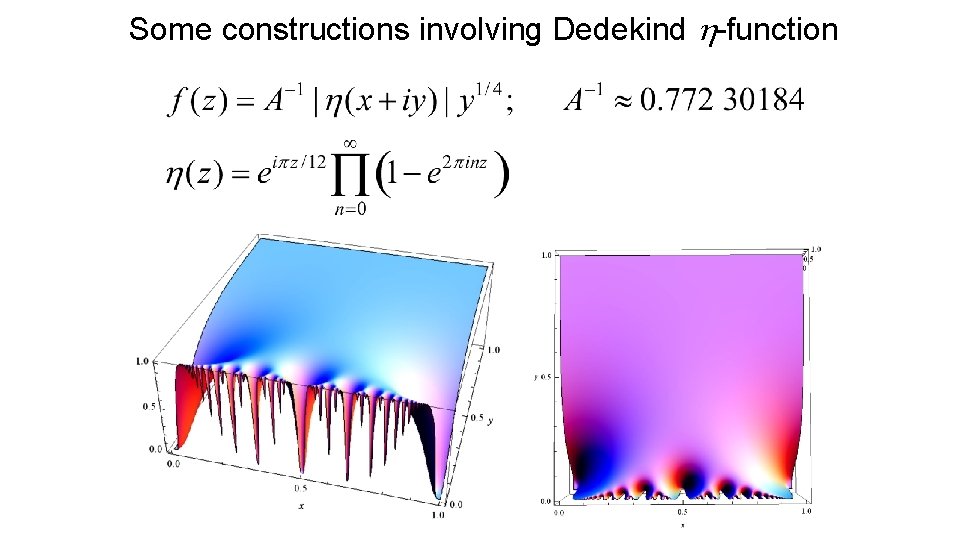
Some constructions involving Dedekind h-function

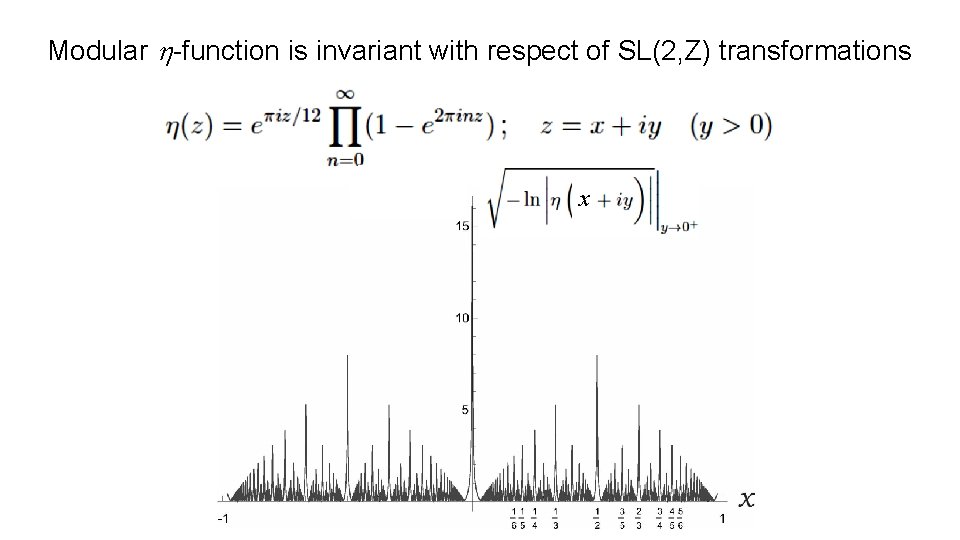
Modular h-function is invariant with respect of SL(2, Z) transformations x

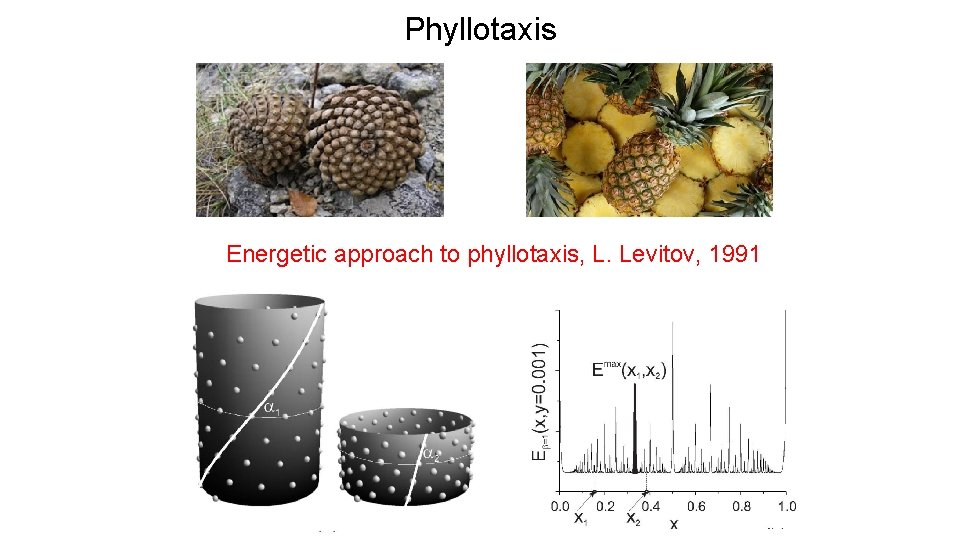
Phyllotaxis Energetic approach to phyllotaxis, L. Levitov, 1991

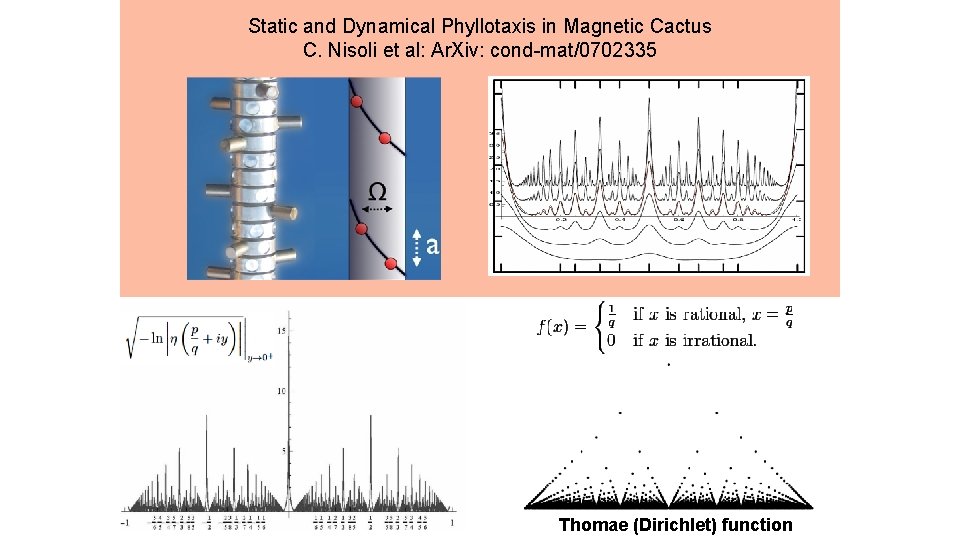
Static and Dynamical Phyllotaxis in Magnetic Cactus C. Nisoli et al: Ar. Xiv: cond-mat/0702335 Thomae (Dirichlet) function