From Bohr Atom to Periodic Table Bohr Atom

From Bohr Atom to Periodic Table • Bohr Atom: electron energy is quantized, n = 1, 2, 3, . . . – are principal quantum numbers: only some definite electron orbits are allowed • Dual nature of electron: particle & wave. Uncertainty principle: one can’t determine at the same time both the position & velocity [hence energy] of electron. Therefore: • Bohr trajectories transform into ORBITALS, i. e. parts of space where electron is likely to be found. Their energies are quantizied • A set of 4 quantum numbers & gives electron density distribution around the atomic nucleus

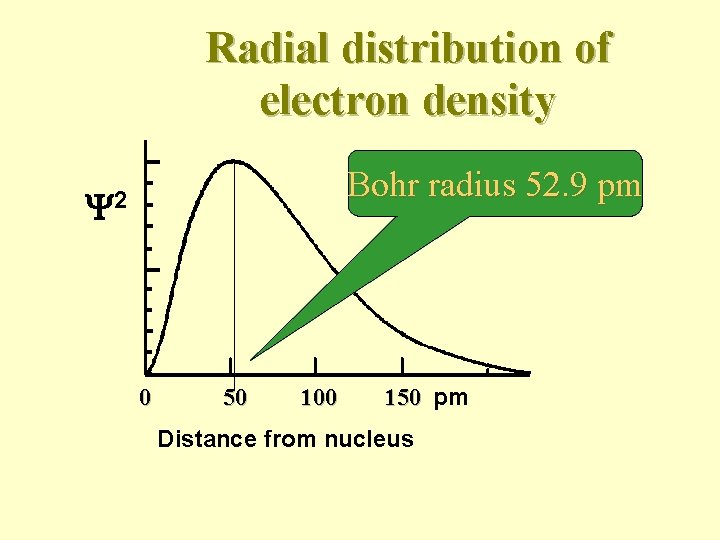
Radial distribution of electron density Bohr radius 52. 9 pm 2 0 50 100 150 pm Distance from nucleus

FOUR QUANTUM NUMBERS Principal quantum # n = 1, 2, 3, … distance &energy Orbital quantum # l = 0, 1, …, n-1 i. e. total n values for each n shape of orbital Magnetic orbital quantum # ml = 0, +1, +2, . . . , +l i. e. total (2 l +1) values for each l Spin quantum # s = + 1/2

Every possible set of quantum #’s n, l, m gives one orbital e. g. n=2, l = 1, ml = 0 Pauli Exclusion Principle there cannot be two electrons in an atom with all their quantum #'s equal.
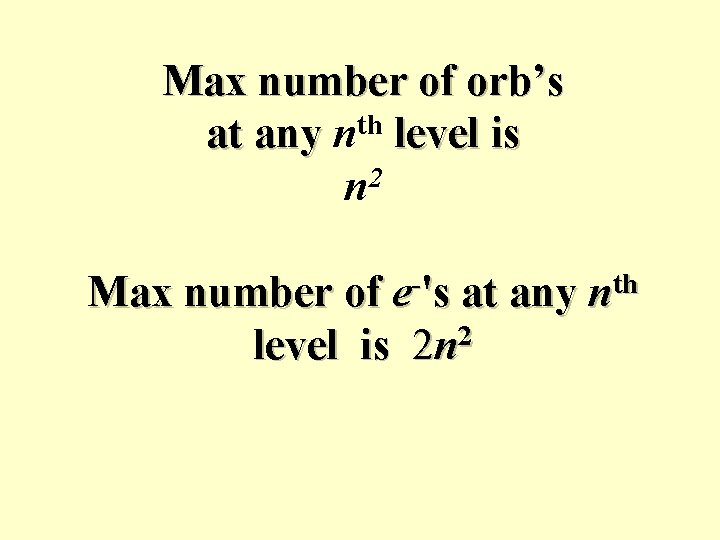
Max number of orb’s at any nth level is 2 n Max number of e-'s at any nth level is 2 n 2


LETTER NOTATIONS

Not every combination make sense! 4 2 p How many more e's possible?



(3) (1) d - orbitals (1)

AUFBAU PRINCIPLE Orbitals are filled with e-'s according to their increasing energies, from bottom to top.

Example: Out of two orbitals with the same n+l =3: n = 3, l = 0 vs. n = 2, l = 1 2 p orbital is filled before 3 s

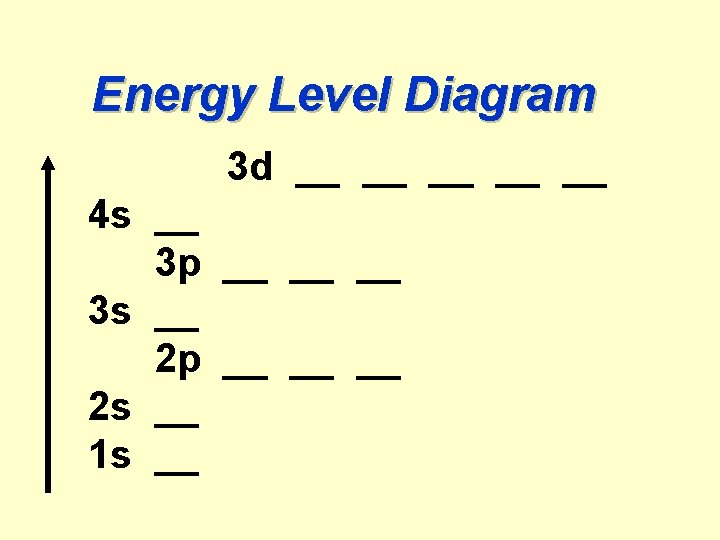
Energy Level Diagram 3 d __ __ __ 4 s __ 3 p __ __ __ 3 s __ 2 p __ __ __ 2 s __ 1 s __

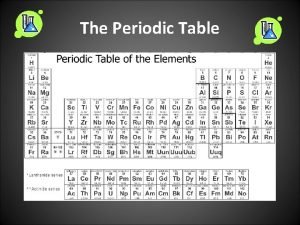
PERIODIC TABLE: s, p, d, f -blocks p s d f

When several orb's of equal energy (“degenerate”) available, e- first fill each of them one by one, all having the same spins ( ). Only after each orbital of the same subshell got one e-, the 2 nd one is placed on the same orbital. Their spins are antiparallel ( , "el. pair")

Example: How many unpaired e-'s are there in 3 p 4 orbital?

ELECTRON PAIRS Each orbital ma be populated by 1 or 2 electrons. Pauli Exclusion Principle: there cannot be two electrons in an orbital, with all their quantum numbers equal. Therefore, if n, l & ml for 2 electrons are the same, i. e. they belong to the same orbital, their SPINS MUST BE OPPOSITE (s = + ½). Those electrons are paired. The physical reason of pairing electrons is that each electron is a small magnet. 2 electrons may cancel each other’s magnetic field (we say they have antiparallel SPINS, this is a more stable situation: an electron pair at the same molecular orbital) or sum up their magnetic field (unstable situation: both electrons cannot belong to the same orbital)

repel S S N N H 2 molecule N S attract electron pair He atom

1 st period H 1 s He 1 s 2 2 nd period Li 1 s 22 s Be 1 s 22 s 2 B 1 s 22 p 1 C 1 s 22 p 2. . . F 1 s 22 p 5 Ne 1 s 22 p 6 … Hund rule 4 th period K 1 s 22 p 63 s 23 p 64 s 1 Ca[Ar]4 s 2 Sc[Ar]4 s 23 d 1…Zn[Ar]4 s 23 d 10 Ga[Ar]4 s 23 d 104 p 1
- Slides: 23