Friday March 23 2018 MAT 146 Friday March





















- Slides: 24

Friday, March 23, 2018 MAT 146

Friday, March 23, 2018 MAT 146

Friday, March 23, 2018 MAT 146

Friday, March 23, 2018 MAT 146

Friday, March 23, 2018 MAT 146

Friday, March 23, 2018 MAT 146

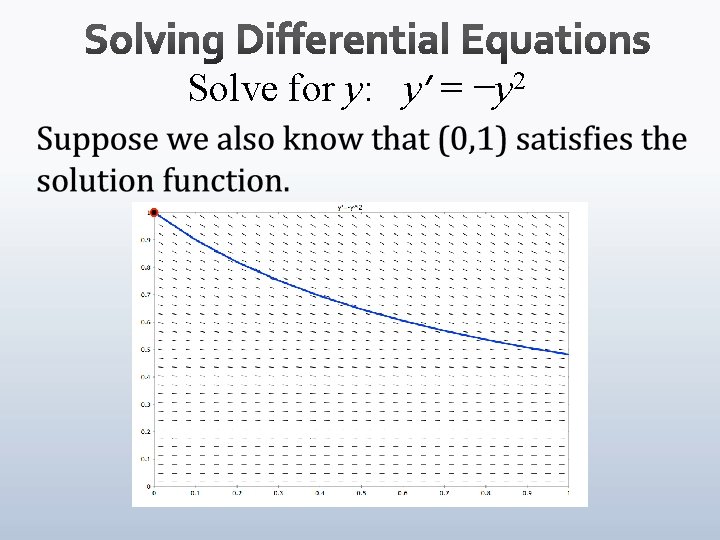
Solve for y: y’ = −y 2 Friday, March 23, 2018 MAT 146

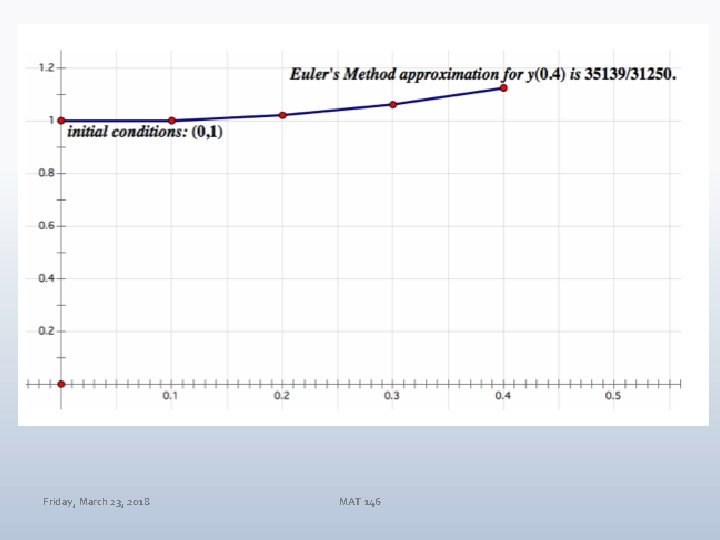
Solve for y: y’ = −y 2 MAT 146

Solve for y: y’ = −y 2, IC: (0, 1) Friday, March 23, 2018 MAT 146

Friday, March 23, 2018 MAT 146

Solve for y: y’ = 3 xy Friday, March 23, 2018 MAT 146

Solve for z: Friday, March 23, 2018 dz/ + dx MAT 146 x + z 5 e =0

Friday, March 23, 2018 MAT 146

Friday, March 23, 2018 MAT 146

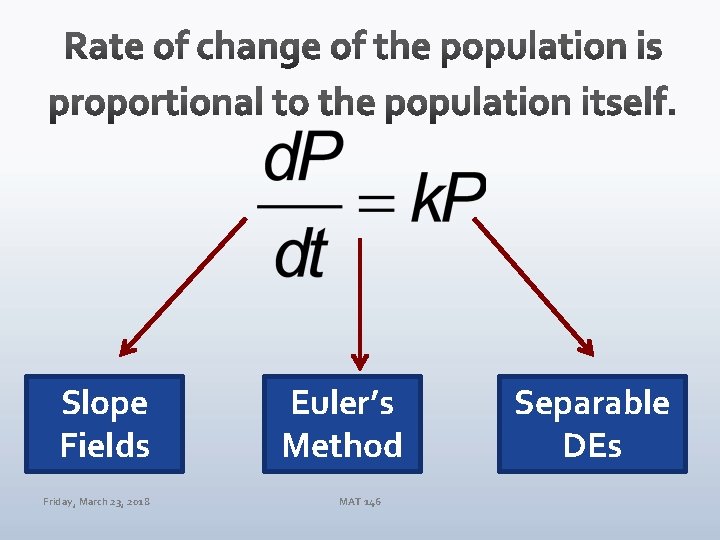
Applications! Rate of change of a population P, with respect to time t, is proportional to the population itself. Friday, March 23, 2018 MAT 146

Slope Fields Friday, March 23, 2018 Euler’s Method MAT 146 Separable DEs

Population Growth Suppose a population increases by 3% each year and that there are P=100 organisms initially present (at t=0). Write a differential equation to describe this population growth and then solve for P. Friday, March 23, 2018 MAT 146

Separable DEs Friday, March 23, 2018 MAT 146

Applications! The radioactive isotope Carbon-14 exhibits exponential decay. That is, the rate of change of the amount present (A) with respect to time (t) is proportional to the amount present (A). Friday, March 23, 2018 MAT 146

Exponential Decay The radioactive isotope Carbon-14 exhibits exponential decay. That is, the rate of change of the amount present (C) with respect to time (t) is proportional to the amount present (C). Carbon-14 has a half-life of 5730 years Write and solve a differential equation to determine the function C(t) to represent the amount, C, of carbon-14 present, with respect to time (t in years), if we know that 20 grams were present initially. Use C(t) to determine the amount present after 250 years. Friday, March 23, 2018 MAT 146

Friday, March 23, 2018 MAT 146

The security staff at a rock concert found a dead body in a mezzanine restroom, the apparent victim of a fatal shooting. They alert the police who arrive at precisely 12 midnight. At that instant, the body’s temperature is 91º F; by 1: 30 a. m. , 90 minutes later, the body’s temperature has dropped to 82º F. Noting that thermostat in the restroom was set to maintain a constant temperature of 69º F, and assuming the victim’s temperature was 98. 6º F when she was shot, determine the time, to the nearest minute, that the fatal shooting occurred. Assume that the victim died instantly and that Newton’s Law of Cooling holds. Show all appropriate evidence to support your solution. Friday, March 23, 2018 MAT 146

Friday, March 23, 2018 MAT 146

Friday, March 23, 2018 MAT 146