Frequent Sequence Mining Efficient frequent sequence mining by

Frequent Sequence Mining Efficient frequent sequence mining by a dynamic strategy switching algorithm Ding-Ying Chiu, Yi-Hung Wu, Arbee L. P. Chen VLDB Journal 2008 Presented by: Ding-Ying Chiu Date: 2008/11/21 1

Outline • Introduction • Basic idea – challenges • Past strategies – Candidate sequence pruning – Database partitioning – Customer sequence reducing • DISC strategy • Future works 2

Introduction Definitions (1/3) Student ID Text books 1 (data structure, statistics) (algorithm, compiler) 2 (data structure, programming language) (algorithm, compiler) 3 (linear algebra, programming language) (compiler) 4 (data structure, linear algebra) (algorithm, computer architecture) Itemset:An itemset is a non-empty set of item. Sequence:A sequence is an ordered list of itemset. Transaction:Each transaction corresponds to an itemset. Customer sequence:All the transactions of a customer are ordered by increasing transaction-times to form a sequence. Length of a sequence:the total number of item occurrences in it. EX:The length of the SID 2 is 4. k-sequence:A k-sequence stands for a sequence with length k. 3
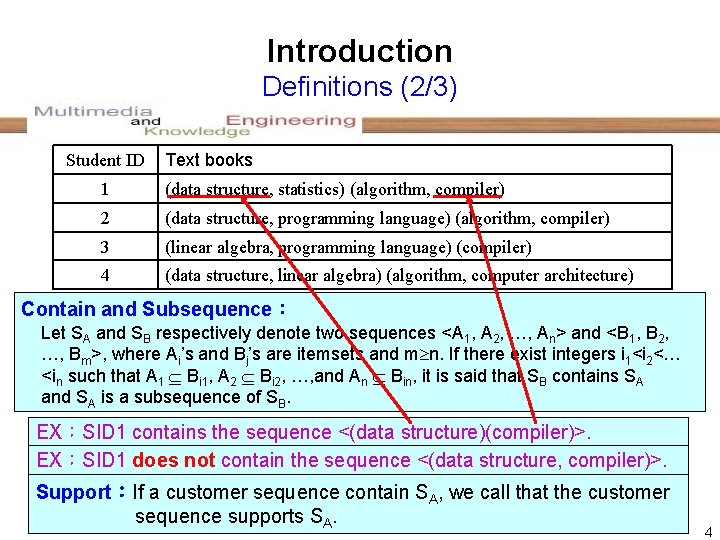
Introduction Definitions (2/3) Student ID Text books 1 (data structure, statistics) (algorithm, compiler) 2 (data structure, programming language) (algorithm, compiler) 3 (linear algebra, programming language) (compiler) 4 (data structure, linear algebra) (algorithm, computer architecture) Contain and Subsequence: Let SA and SB respectively denote two sequences <A 1, A 2, …, An> and <B 1, B 2, …, Bm>, where Ai’s and Bj’s are itemsets and m n. If there exist integers i 1<i 2<… <in such that A 1 Bi 1, A 2 Bi 2, …, and An Bin, it is said that SB contains SA and SA is a subsequence of SB. EX:SID 1 contains the sequence <(data structure)(compiler)>. EX:SID 1 does not contain the sequence <(data structure, compiler)>. Support:If a customer sequence contain SA, we call that the customer sequence supports SA. 4
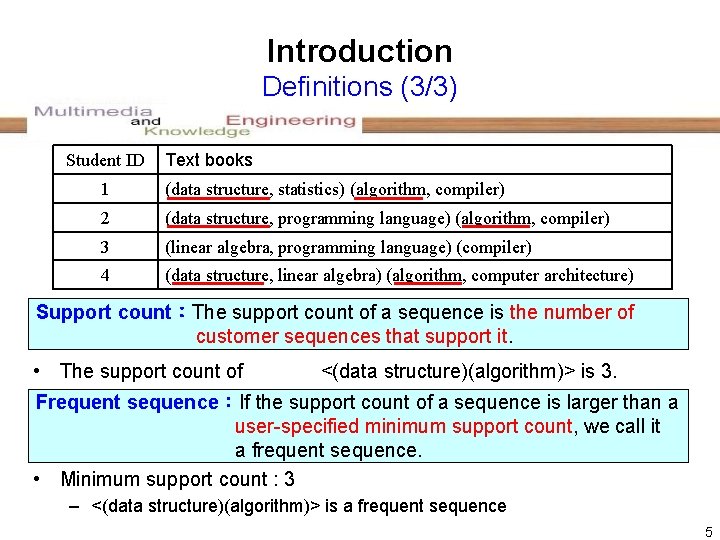
Introduction Definitions (3/3) Student ID Text books 1 (data structure, statistics) (algorithm, compiler) 2 (data structure, programming language) (algorithm, compiler) 3 (linear algebra, programming language) (compiler) 4 (data structure, linear algebra) (algorithm, computer architecture) Support count:The support count of a sequence is the number of customer sequences that support it. • The support count of <(data structure)(algorithm)> is 3. Frequent sequence:If the support count of a sequence is larger than a user-specified minimum support count, we call it a frequent sequence. • Minimum support count : 3 – <(data structure)(algorithm)> is a frequent sequence 5

Introduction Problem Definition Student ID Text books 1 (data structure, statistics) (algorithm, compiler) 2 (data structure, programming language) (algorithm, compiler) 3 (linear algebra, programming language) (compiler) 4 (data structure, linear algebra) (algorithm, computer architecture) Frequent sequence mining Minimum support count : 3 frequent 1 -sequence : <(data structure)>, <(algorithm)>, <(compiler)> frequent 2 -sequence : <(data structure)(algorithm)> Difference from Association Rules 1. Transaction vs. Customer sequence 2. Order <(data structure)(algorithm)> <(algorithm)(data structure)> 6

Basic idea • Computing the support count for each sequence CID Customer Sequence 1 (c, d)(a, b, c)(a, b, f)(a, c, d, f) <a> 2 (a, b, f)(e) <b> 3 (a, b, f) <c> 4 (d, g, h)(b, f)(a, g, h) minimum support count = 2 Support count <d> <e> <f> Frequent 1 -sequence: <(a)>, <(b)>, <(d)>, <(f)> <g> <h> 7

Challenges (1) The number of candidate k-sequence • Computing the support count for each sequence 1 (c, d)(a, b, c)(a, b, f)(a, c, d, f) Sequenc e 2 (a, b, f)(e) <(a)(a)> 3 (a, b, f) <(a)(b)> 4 (d, g, h)(b, f)(a, g, h) CID Customer Sequence Support count <(ab)> minimum support count = 2 If there are 1000 items, when computing the support count for k-sequence, the number of candidate k-sequence is . . . <(h)(h)> K=2 1, 000 Main memory 8

Challenges (2) The number of decomposition • Computing the support count for each sequence 1 (c, d)(a, b, c)(a, b, f)(a, c, d, f) (c)(a) Sequenc e 2 (a, b, f)(e) (c)(b) <(a)(a)> 3 (a, b, f) <(a)(b)> 4 (d, g, h)(b, f)(a, g, h) . . . CID Customer Sequence minimum support count = 2 (c, d) (c)(f) (d)(a) . . . (d, f) Support count <(ab)>. . . <(h)(h)> 9

Past strategies If there are 1000 items, when computing the support count for k-sequence, the number of candidate k-sequence is • Two Challenges – The number of candidate k-sequence – The number of decomposition • Candidate sequence pruning – Challenge 1 • Database partitioning • Customer sequence reducing – Challenge 2 10

Candidate sequence pruning Anti-monotone property • Anti-monotone property – If a sequence cannot pass a test, all of its super-sequences will fail the same test as well. Student ID Text books 1 (data structure, statistics) (algorithm, compiler) 2 (data structure, programming language) (algorithm, compiler) 3 (linear algebra, programming language) (compiler) 4 (data structure, linear algebra) (algorithm, computer architecture) Minimum support count : 3 The count of <(data structure), (compiler)> is 2. The count of <(data structure, programming language), (compiler)> is 1. The count of <(data structure), (algorithm, compiler)> is 2. 2 11
![GSP [19] Main idea • Anti-monotone property – If a sequence cannot pass a GSP [19] Main idea • Anti-monotone property – If a sequence cannot pass a](http://slidetodoc.com/presentation_image_h2/51e8ceae64012f2fe58011e890ac9e63/image-12.jpg)
GSP [19] Main idea • Anti-monotone property – If a sequence cannot pass a test, all of its super-sequences will fail the same test as well. CID Sequence If <(a)(b)> is not the frequent 2 -sequence, the <(a)(b)(c)> is not the frequent 3 -sequence. 1 (c, d)(a, b, c)(a, b, f)(a, c, d, f) 2 (a, b, f)(e) 3 (a, b, f) 4 (d, g, h)(b, f)(a, g, h) minimum support = 2 Using the anti-monotone property, the sequence <(a)(b)(c)> will not be generated in candidate 3 -sequence. 12
![GSP [19] Overview • GSP generates candidate k-sequences from frequent (k-1)-sequences in iteration based GSP [19] Overview • GSP generates candidate k-sequences from frequent (k-1)-sequences in iteration based](http://slidetodoc.com/presentation_image_h2/51e8ceae64012f2fe58011e890ac9e63/image-13.jpg)
GSP [19] Overview • GSP generates candidate k-sequences from frequent (k-1)-sequences in iteration based on the anti-monotone property. Anti-monotone property Join step Prune step Frequent 1 -sequences Candidate 2 -sequences Frequent 2 -sequences . . . Frequent (n-1)-sequences Candidate n-sequences Frequent n-sequences 13
![GSP [19] Join Step & Prune Step • Join step Let f 1 and GSP [19] Join Step & Prune Step • Join step Let f 1 and](http://slidetodoc.com/presentation_image_h2/51e8ceae64012f2fe58011e890ac9e63/image-14.jpg)
GSP [19] Join Step & Prune Step • Join step Let f 1 and f 2 be itemsets in frequent (k-1)-sequence set. The join is performed, where their first (k-2) items are in common. • Prune step CID Sequence 1 (c, d)(a, b, c)(a, b, f)(a, c, d, f) 2 (a, b, f)(e) 3 (a, b, f) 4 (d, g, h)(b, f)(a, g, h) We delete candidate sequences that have a contiguous (k-1)minimum support = 2 subsequence whose support count is less than the minimum support Frequent 2 -sequences: count. <(ab)>: 3 <(af)>: 3 <(b)(a)>: 2 <(bf)>: 4 <(d)(a)>: 2 <(d)(b)>: 2 <(d)(f)>: 2 <(f)(a)>: 2 In join step: <(d)(a)> join <(d)(b)> <(d)(ab)>, <(d)(a)(b)> and <(d)(b)(a)> In prune step: the <(d)(a)(b)> be pruned because <(a)(b)> is not a frequent 2 -sequence 14

![GSP [19] minsup = 2 CID Sequence 1 (c, d)(a, b, c)(a, b, f)(a, GSP [19] minsup = 2 CID Sequence 1 (c, d)(a, b, c)(a, b, f)(a,](http://slidetodoc.com/presentation_image_h2/51e8ceae64012f2fe58011e890ac9e63/image-16.jpg)
GSP [19] minsup = 2 CID Sequence 1 (c, d)(a, b, c)(a, b, f)(a, c, d, f) 2 (a, b, f)(e) 3 (a, b, f) 4 (d, g, h)(b, f)(a, g, h) Frequent 1 -sequences: <a>: 4 <b>: 4 <d>: 2 Frequent 2 -sequences: <(ab)>: 3 <(af)>: 3 <(b)(a)>: 2 <(bf)>: 4 <(d)(a)>: 2 <(d)(b)>: 2 <(d)(f)>: 2 <(f)(a)>: 2 Candidate 3 -sequences: <(abf)> <(b)(a)(a)> <(bf)(a)> <(d)(ab)> <(d)(a)(b)> <(d)(af)> <(d)(a)(f)> <(d)(b)(a)> <(d)(b)(b)> <(d)(bf)> <(d)(b)(f)> <(d)(f)(a)> <(d)(f)(b)> <(d)(f)(f)> <f>: 4 Candidate 2 -sequences: <(a)(a)> <(a)(b)> <(a)(d)> <(a)(f)> <(af)> <(b)(a)> <(b)(b)> <(b)(d)> <(b)(f)> <(bf)> <(d)(a)> <(d)(b)> <(d)(d)> <(d)(f)> <(df)> <(f)(a)> <(f)(b)> <(f)(c)> <(f)(d)> Frequent 3 -sequences: <(abf)>: 3 <(bf)(a)>: 2 <(d)(bf)>: 2 <(d)(b)(a)>: 2 <(d)(f)(a)>: 2 Candidate 4 -sequences: <(d)(bf)(a)> Frequent 4 -sequences: <(d)(bf)(a)>: 2 16
Past strategies If there are 1000 items, when computing the support count for k-sequence, the number of candidate k-sequence is • Two Challenges – The number of candidate k-sequence – The number of decomposition • Candidate sequence pruning – Challenge 1 GSP [19] • Database partitioning Prefix. Span [13] • Customer sequence reducing – Challenge 2 17
![Prefix. Span [13] Definitions • Prefix: Give a sequence = <e 1 e 2…en>, Prefix. Span [13] Definitions • Prefix: Give a sequence = <e 1 e 2…en>,](http://slidetodoc.com/presentation_image_h2/51e8ceae64012f2fe58011e890ac9e63/image-18.jpg)
Prefix. Span [13] Definitions • Prefix: Give a sequence = <e 1 e 2…en>, a sequence = <e’ 1 e’ 2…e’m> is called a prefix of if and only if (1) e’i=ei for ( I m-1 ) (2) e’m em (3) all the item in ( em - e’m ) are alphabetically after those in e’m. Example: = <(a)(abc)(ac)(d)(cf)> <(a)(a)> is a prefix of <(a)(abc)> is a prefix of <(a)(bc)> is not a prefix of 18
![Prefix. Span [13] Projected Database • A projected database is a sequence set such Prefix. Span [13] Projected Database • A projected database is a sequence set such](http://slidetodoc.com/presentation_image_h2/51e8ceae64012f2fe58011e890ac9e63/image-19.jpg)
Prefix. Span [13] Projected Database • A projected database is a sequence set such that each sequence is a subsequence of a customer sequence and they have the same prefix which corresponds to a frequent sequence. CID Customer Sequence 1 (c, d)(a, b, c)(a, b, f)(a, c, d, f) 1 (_, b, c)(a, b, f)(a, c, d, f) 2 (a, b, f)(e) 2 (_, b, f)(e) 3 (a, b, f) 3 (_, b, f) 4 (d, g, h)(b, f)(a, g, h) Original database 4 (_, g, h) <a>-projected database a is the prefix 19
![Prefix. Span [13] Projected Database • A important characteristic of projected database is that Prefix. Span [13] Projected Database • A important characteristic of projected database is that](http://slidetodoc.com/presentation_image_h2/51e8ceae64012f2fe58011e890ac9e63/image-20.jpg)
Prefix. Span [13] Projected Database • A important characteristic of projected database is that the prefix < > combining any frequent sequence < > can generate a longer frequent sequence < >. CID Customer Sequence 1 (_, b, c)(a, b, f)(a, c, d, f) 2 (_, b, f)(e) 3 (_, b, f) 4 (_, g, h) <a>-projected database Minimum Support count = 2 Frequent 1 -sequence: <b>, <f> <(ab)> and <(af)> are frequent 2 -sequences 20

Strategies Database partitioning • This strategy eliminates the unnecessary decompositions of customer sequences while adding the extra costs for partitioning the database. CID Customer Sequence 1 (b, d)(b, f, g)(a, e) 2 (d, g, h)(c, e) 1 (_, e) 3 (b, f)(a, c, d) 3 (_, c, d) 4 (b, c, h)(c, h, i) 5 (_, d)(e, f, g) 5 (b, d, e)(a, d)(e, f, g) <a>-projected database Original database 21
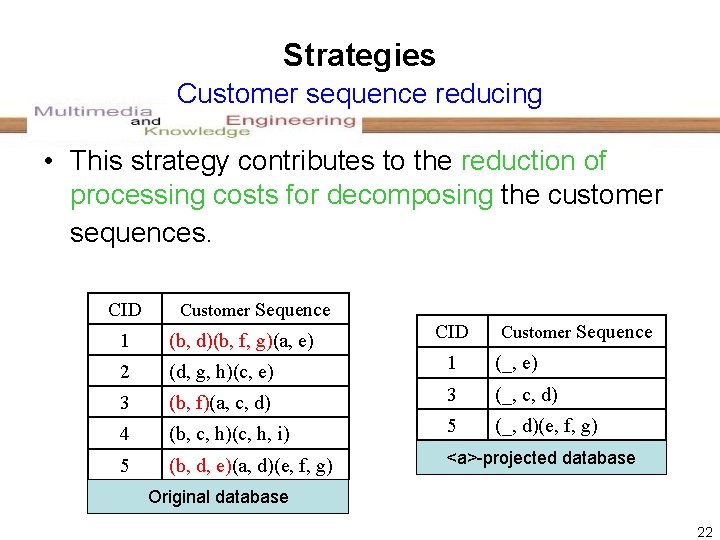
Strategies Customer sequence reducing • This strategy contributes to the reduction of processing costs for decomposing the customer sequences. CID Customer Sequence 1 (b, d)(b, f, g)(a, e) 2 (d, g, h)(c, e) 1 (_, e) 3 (b, f)(a, c, d) 3 (_, c, d) 4 (b, c, h)(c, h, i) 5 (_, d)(e, f, g) 5 (b, d, e)(a, d)(e, f, g) <a>-projected database Original database 22
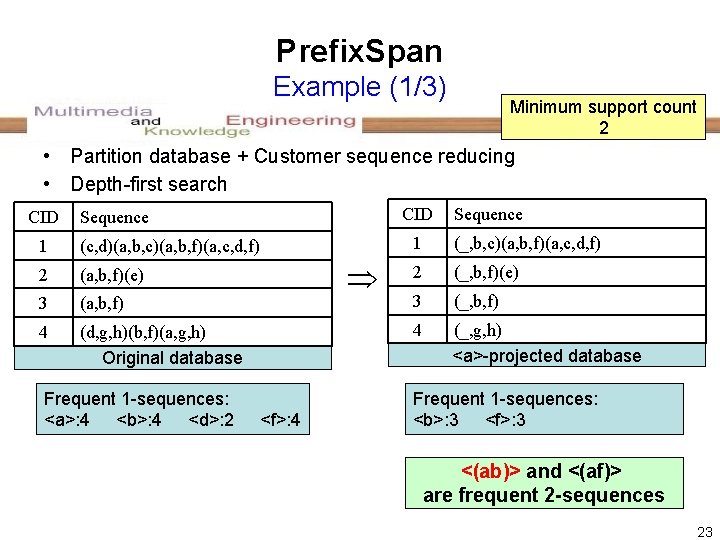
Prefix. Span Example (1/3) Minimum support count 2 • Partition database + Customer sequence reducing • Depth-first search CID Sequence 1 (c, d)(a, b, c)(a, b, f)(a, c, d, f) 2 (a, b, f)(e) 3 (a, b, f) 4 (d, g, h)(b, f)(a, g, h) Original database Frequent 1 -sequences: <a>: 4 <b>: 4 <d>: 2 <f>: 4 Sequence 1 (_, b, c)(a, b, f)(a, c, d, f) 2 (_, b, f)(e) 3 (_, b, f) 4 (_, g, h) <a>-projected database Frequent 1 -sequences: <b>: 3 <f>: 3 <(ab)> and <(af)> are frequent 2 -sequences 23
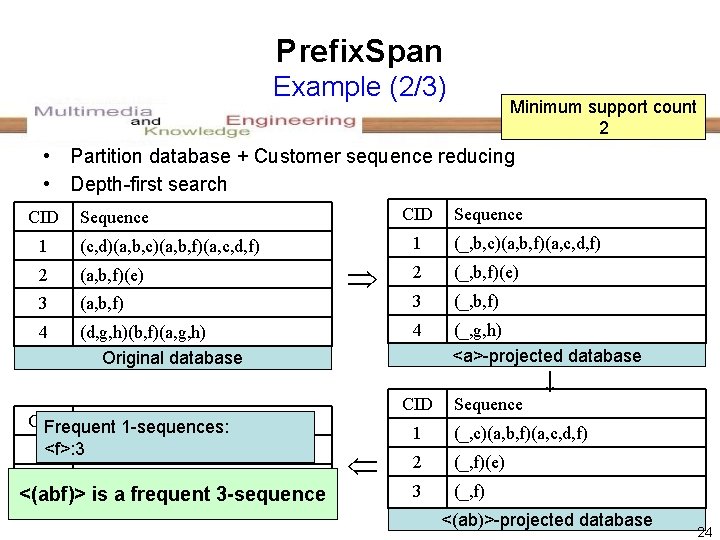
Prefix. Span Example (2/3) Minimum support count 2 • Partition database + Customer sequence reducing • Depth-first search CID 1 (c, d)(a, b, c)(a, b, f)(a, c, d, f) 2 (a, b, f)(e) 3 (a, b, f) 4 (d, g, h)(b, f)(a, g, h) Original database CID Sequence Frequent 1 -sequences: 1<f>: 3(a, c, d, f) 2 CID Sequence (e) <(abf)> is a frequent 3 -sequence <(abf)>-projected database Sequence 1 (_, b, c)(a, b, f)(a, c, d, f) 2 (_, b, f)(e) 3 (_, b, f) 4 (_, g, h) <a>-projected database ↓ CID Sequence 1 (_, c)(a, b, f)(a, c, d, f) 2 (_, f)(e) 3 (_, f) <(ab)>-projected database 24
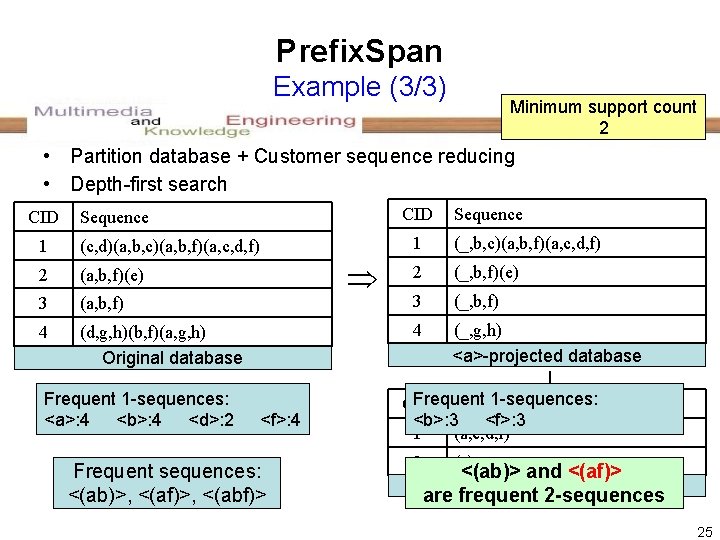
Prefix. Span Example (3/3) Minimum support count 2 • Partition database + Customer sequence reducing • Depth-first search CID Sequence 1 (c, d)(a, b, c)(a, b, f)(a, c, d, f) 2 (a, b, f)(e) 3 (a, b, f) 4 (d, g, h)(b, f)(a, g, h) Original database Frequent 1 -sequences: <a>: 4 <b>: 4 <d>: 2 Sequence 1 (_, b, c)(a, b, f)(a, c, d, f) 2 (_, b, f)(e) 3 (_, b, f) 4 (_, g, h) <a>-projected database ↓ <f>: 4 Frequent sequences: <(ab)>, <(af)>, <(abf)> Frequent 1 -sequences: CID Sequence <b>: 3 <f>: 3 1 (a, c, d, f) 2 (e) <(ab)> and <(af)>-projected database are frequent 2 -sequences 25
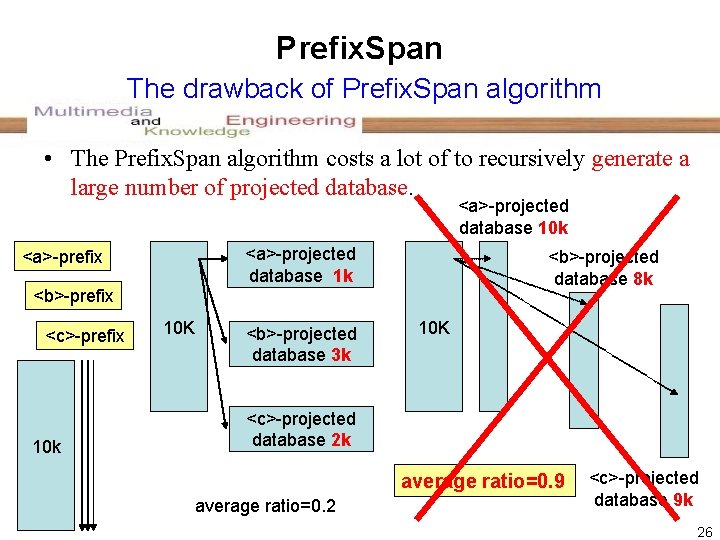
Prefix. Span The drawback of Prefix. Span algorithm • The Prefix. Span algorithm costs a lot of to recursively generate a large number of projected database. <a>-projected database 10 k <a>-projected database 1 k <a>-prefix <b>-projected database 8 k <b>-prefix <c>-prefix 10 k 10 K <b>-projected database 3 k 10 K <c>-projected database 2 k average ratio=0. 9 average ratio=0. 2 <c>-projected database 9 k 26
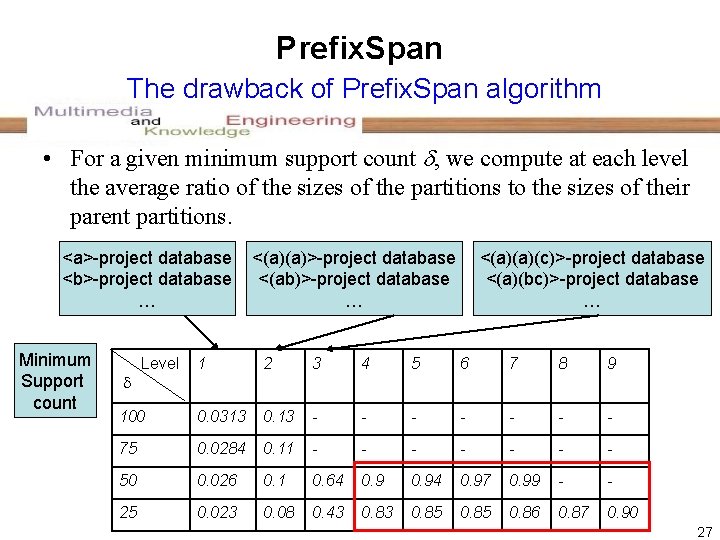
Prefix. Span The drawback of Prefix. Span algorithm • For a given minimum support count , we compute at each level the average ratio of the sizes of the partitions to the sizes of their parent partitions. <a>-project database <b>-project database … Minimum Support count <(a)(a)(c)>-project database <(a)(bc)>-project database … 1 2 3 4 5 6 7 8 9 100 0. 0313 0. 13 - - - - 75 0. 0284 0. 11 - - - - 50 0. 026 0. 1 0. 64 0. 94 0. 97 0. 99 - - 25 0. 023 0. 08 0. 43 0. 85 0. 86 0. 87 0. 90 Level <(a)(a)>-project database <(ab)>-project database … 27
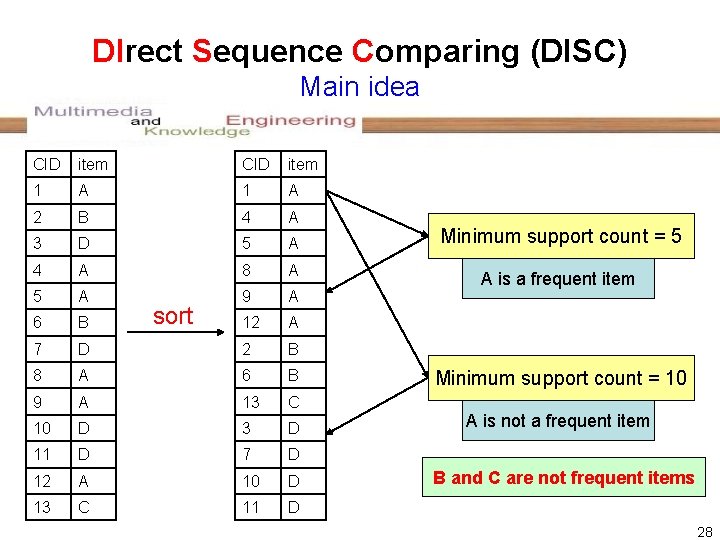
DIrect Sequence Comparing (DISC) Main idea CID item 1 A 2 B 4 A 3 D 5 A 4 A 8 A 5 A 9 A 6 B 12 A 7 D 2 B 8 A 6 B 9 A 13 C 10 D 3 D 11 D 7 D 12 A 10 D 13 C 11 D sort Minimum support count = 5 A is a frequent item Minimum support count = 10 A is not a frequent item B and C are not frequent items 28

DIrect Sequence Comparing (DISC) Definition • Differential Point 1. Item 2. transaction number A = <(a 1 b 1 d 1)(a 2 b 2)> B = <(a 1 b 1 c 1)(b 2 c 2)> C = <(a 1 b 1)(d 2)(a 3 b 3 e 3)> DP(AB)=3, DP(AC)=3, DP(BC)=3 • Comparative order 1. 2. alphabetical order The sequence which is with the preceding item in the same transaction is smaller. B< A <C 29

DIrect Sequence Comparing (DISC) minimum k-subsequence • minimum k-subsequence <(abc)(cd)(bcd)(ad)> 3: <(abc)>, <(ac)(d)> ……,the <(a)(ad)> is minimum 4: <(ab)(ad)> 5: <(ab)(b)(ad)> • The min-k ordered database CID Customer sequence Minimum 3 -subsequence 1 (a, e, g)1 (b)2 (h)3 (f)4 (c)5 (b, f)6 (a)1 (b)2 (b)3 4 (f)1 (a, g)2 (b, f, h)3 (b, f)4 (a)1 (b)2 (b)3 2 (b)1 (d, f)2 (e)3 (b)1 (d)2 (e)3 3 (b, f, g)1 30

DIrect Sequence Comparing (DISC) Advantage CID Customer sequence Minimum 3 -subsequence 1 (a, e, g)1 (b)2 (h)3 (f)4 (c)5 (b, f)6 (a)1 (b)2 (b)3 4 (f)1 (a, g)2 (b, f, h)3 (b, f)4 (a)1 (b)2 (b)3 2 (b)1 (d, f)2 (e)3 (b)1 (d)2 (e)3 3 (b, f, g)1 • Minimum Support count = 2 : <(a)(b)(b)> is a frequent sequence • Minimum Support count = 3 : <(a)(b)(b)> isn’t a frequent sequence • Avoid unnecessary decomposition – When minimum support count = 3 : – the <(a)(b)(c)>, <(a)(bf)>, <(b)(c)(b)> …… are not frequent sequences 31

DIrect Sequence Comparing (DISC) conditional minimum k-subsequence CID Customer sequence Minimum 3 -subsequence 1 (a, e, g)1 (b)2 (h)3 (f)4 (c)5 (b, f)6 (a)1 (b)2 (b)3 4 (f)1 (a, g)2 (b, f, h)3 (b, f)4 (a)1 (b)2 (b)3 2 (b)1 (d, f)2 (e)3 (b)1 (d)2 (e)3 3 (b, f, g)1 • We generate the conditional minimum 3 -subsequence, which should be larger than or equal to <(b)(d)(e)>. Minimum support count <(a, e, g)(b)(h)(f)(c)(b, f)> <(b)(f)(b)> 3 <(f)(a, g)(b, f, h)(b, f)> <(b, f)(b)> CID Customer sequence Minimum 3 -subsequence 2 (b)1 (d, f)2 (e)3 (b)1 (d)2 (e)3 4 (f)1 (a, g)2 (b, f, h)3 (b, f)4 (b, f)1 (b)2 3 (b, f, g)1 1 (a, e, g)1 (b)2 (h)3 (f)4 (c)5 (b, f)6 (b)1 (f)2 (b)3 32
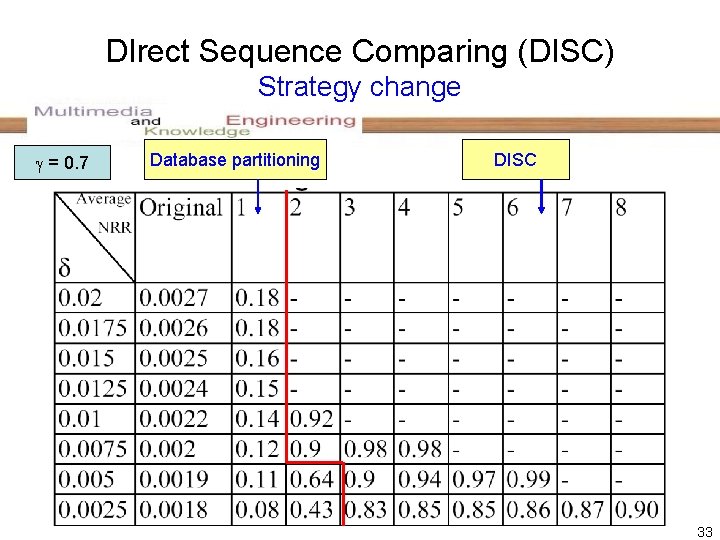
DIrect Sequence Comparing (DISC) Strategy change = 0. 7 Database partitioning DISC 33

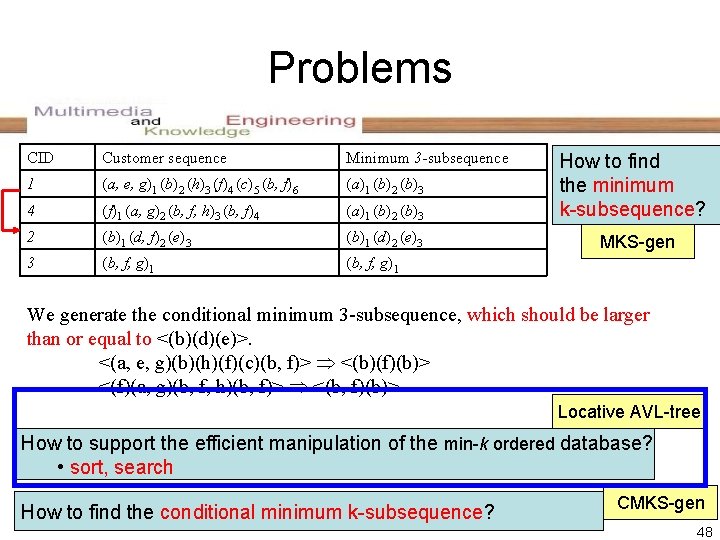
Problems CID Customer sequence Minimum 3 -subsequence 1 (a, e, g)1 (b)2 (h)3 (f)4 (c)5 (b, f)6 (a)1 (b)2 (b)3 4 (f)1 (a, g)2 (b, f, h)3 (b, f)4 (a)1 (b)2 (b)3 How to find the minimum k-subsequence? 2 (b)1 (d, f)2 (e)3 (b)1 (d)2 (e)3 MKS-gen 3 (b, f, g)1 We generate the conditional minimum 3 -subsequence, which should be larger than or equal to <(b)(d)(e)>. <(a, e, g)(b)(h)(f)(c)(b, f)> <(b)(f)(b)> <(f)(a, g)(b, f, h)(b, f)> <(b, f)(b)> Locative AVL-tree How to support the efficient manipulation of the min-k ordered database? • sort, search How to find the conditional minimum k-subsequence? CMKS-gen 34

Minimum k-subsequence Observation • (b, c, d)(b, f, g)(b, d, e, f)(a, g)(b, c) – Minimum 3 -subsequence: (a)(b, c) – Minimum 4 -subsequence: (a, g)(b, c) – Minimum 5 -subsequence: (b)(a, g)(b, c) • Length 1 2 3 4 5 6 7 8 9 10 11 12 13 14 • (b, c, d)(b, f, g)(b, d, e, f)(a, g)(b, c) – Minimum 5 -subsequence: (b)(a, g)(b, c) – n = 14 , k = 5 14 -5+1=10 35

Minimum k-subsequence Greedy-MKS (1/2) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 • (b, c, d)(b, f, g)(b, d, e, f)(a, g)(b, c) (b) – Minimum 5 -subsequence – n = 14 , k = 5 14 -5+1=10 1 2 3 4 5 6 7 8 9 10 11 12 13 • (c, d)(b, f, g)(b, d, e, f)(a, g)(b, c) – Minimum 4 -subsequence – n = 13 , k = 4 13 -4+1=10 1 2 (b)(a) 3 • (g)(b, c) – Minimum 3 -subsequence – n = 3 , k = 3 3 -3+1=1 (b)(a, g) 36
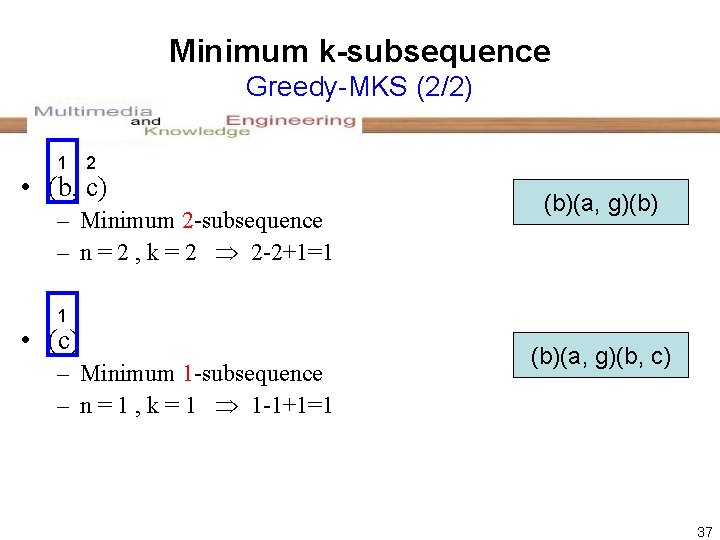
Minimum k-subsequence Greedy-MKS (2/2) 1 2 • (b, c) – Minimum 2 -subsequence – n = 2 , k = 2 2 -2+1=1 (b)(a, g)(b) 1 • (c) – Minimum 1 -subsequence – n = 1 , k = 1 1 -1+1=1 (b)(a, g)(b, c) 37

Greedy-MKS drawback (1/2) • (a, b, c)(d, e, f)(g, h, i, j)(k, l)(m, n)(o, p, q)(r, s, t) – Minimum 3 -subsequence – n = 20 , k = 3 20 -3+1=18 • (b, c)(d, e, f)(g, h, i, j)(k, l)(m, n)(o, p, q)(r, s, t) – Minimum 2 -subsequence – n = 19 , k = 2 19 -2+1=18 • (c)(d, e, f)(g, h, i, j)(k, l)(m, n)(o, p, q)(r, s, t) – Minimum 1 -subsequence – n = 18 , k = 1 18 -1+1=18 Worst case kn 38
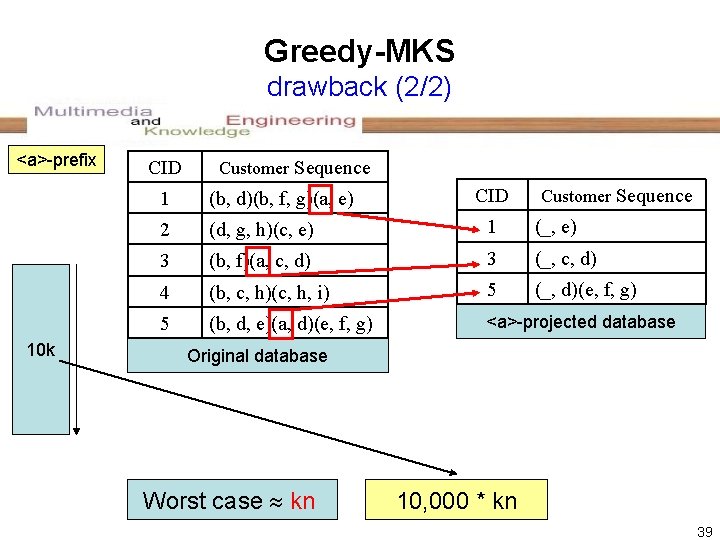
Greedy-MKS drawback (2/2) <a>-prefix 10 k CID Customer Sequence 1 (b, d)(b, f, g)(a, e) 2 (d, g, h)(c, e) 1 (_, e) 3 (b, f)(a, c, d) 3 (_, c, d) 4 (b, c, h)(c, h, i) 5 (_, d)(e, f, g) 5 (b, d, e)(a, d)(e, f, g) <a>-projected database Original database Worst case kn 10, 000 * kn 39
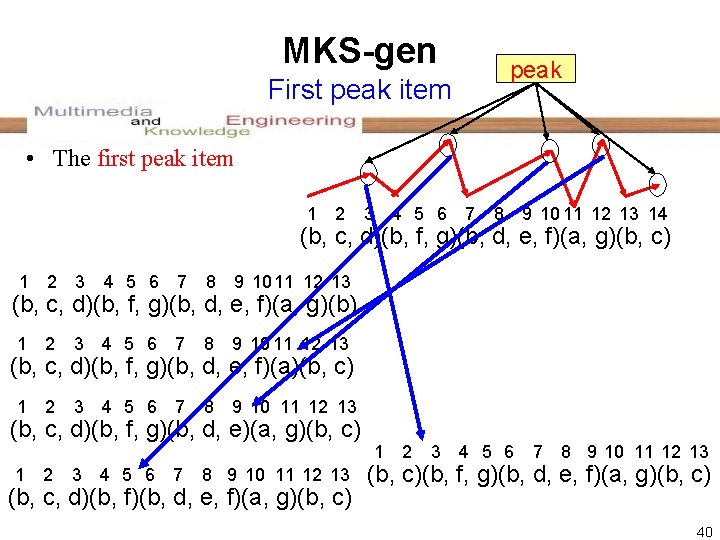
MKS-gen peak First peak item • The first peak item 1 2 3 4 5 6 7 8 9 10 11 12 13 14 (b, c, d)(b, f, g)(b, d, e, f)(a, g)(b, c) 1 2 3 4 5 6 7 8 9 10 11 12 13 (b, c, d)(b, f, g)(b, d, e, f)(a, g)(b) (b, c, d)(b, f, g)(b, d, e, f)(a)(b, c) (b, c, d)(b, f, g)(b, d, e)(a, g)(b, c) 1 1 2 3 4 5 6 7 8 9 10 11 12 13 (b, c, d)(b, f)(b, d, e, f)(a, g)(b, c) 2 3 4 5 6 7 8 9 10 11 12 13 (b, c)(b, f, g)(b, d, e, f)(a, g)(b, c) 40
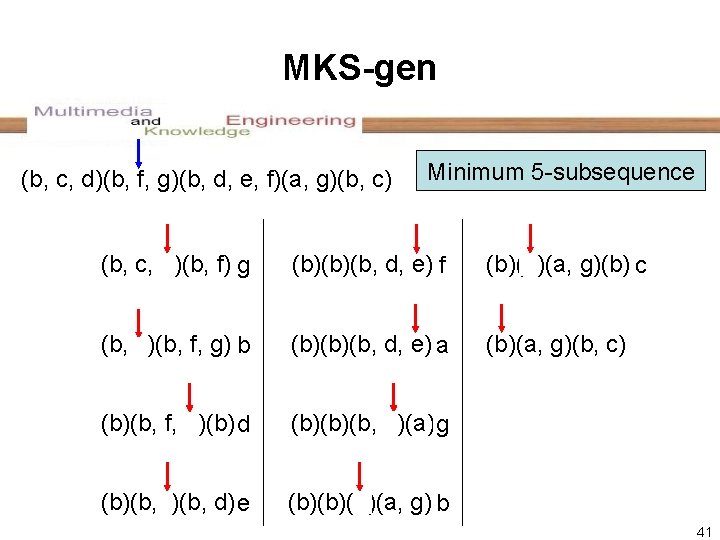
MKS-gen (b, c, d)(b, f, g)(b, d, e, f)(a, g)(b, c) Minimum 5 -subsequence (b, c, d)(b, f) g (b)(b)(b, d, e) f (b)(b)(a, g)(b) c (b, c)(b, f, g) b (b)(b)(b, d, e) a (b)(a, g)(b, c) (b)(b, f, g)(b) d (b)(b)(b, d)(a) g (b)(b, f)(b, d) e (b)(b)(b)(a, g) b 41

Problems CID Customer sequence Minimum 3 -subsequence 1 (a, e, g)1 (b)2 (h)3 (f)4 (c)5 (b, f)6 (a)1 (b)2 (b)3 4 (f)1 (a, g)2 (b, f, h)3 (b, f)4 (a)1 (b)2 (b)3 How to find the minimum k-subsequence? 2 (b)1 (d, f)2 (e)3 (b)1 (d)2 (e)3 MKS-gen 3 (b, f, g)1 We generate the conditional minimum 3 -subsequence, which should be larger than or equal to <(b)(d)(e)>. <(a, e, g)(b)(h)(f)(c)(b, f)> <(b)(f)(b)> <(f)(a, g)(b, f, h)(b, f)> <(b, f)(b)> Locative AVL-tree How to support the efficient manipulation of the min-k ordered database? • sort, search How to find the conditional minimum k-subsequence? CMKS-gen 42
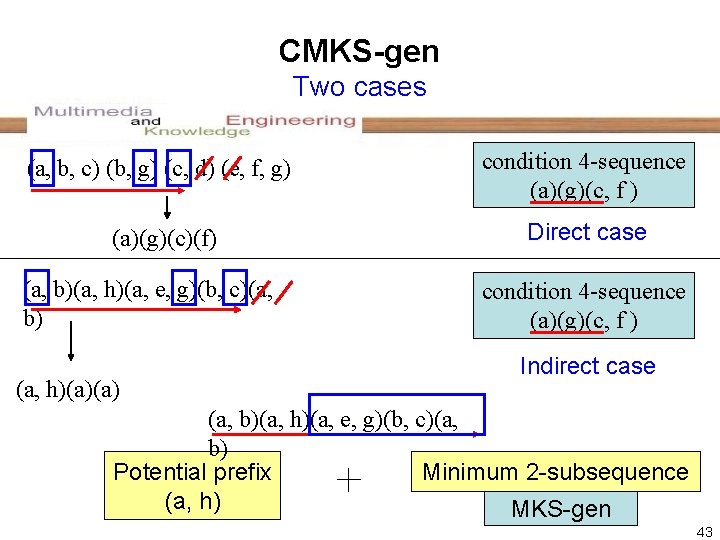
CMKS-gen Two cases (a, b, c) (b, g) (c, d) (e, f, g) condition 4 -sequence (a)(g)(c, f ) (a)(g)(c)(f) Direct case (a, b)(a, h)(a, e, g)(b, c)(a, b) (a, h)(a)(a) condition 4 -sequence (a)(g)(c, f ) Indirect case (a, b)(a, h)(a, e, g)(b, c)(a, b) Potential prefix Minimum 2 -subsequence (a, h) MKS-gen 43
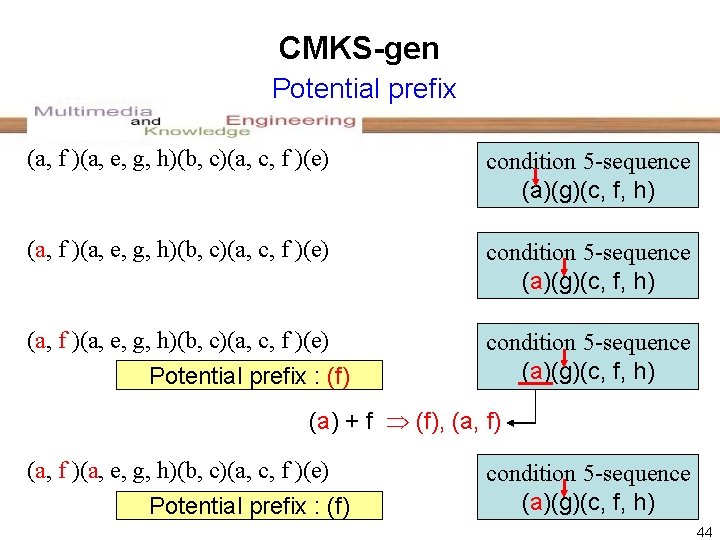
CMKS-gen Potential prefix (a, f )(a, e, g, h)(b, c)(a, c, f )(e) condition 5 -sequence (a)(g)(c, f, h) (a, f )(a, e, g, h)(b, c)(a, c, f )(e) Potential prefix : (f) condition 5 -sequence (a)(g)(c, f, h) (a) + f (f), (a, f) (a, f )(a, e, g, h)(b, c)(a, c, f )(e) Potential prefix : (f) condition 5 -sequence (a)(g)(c, f, h) 44
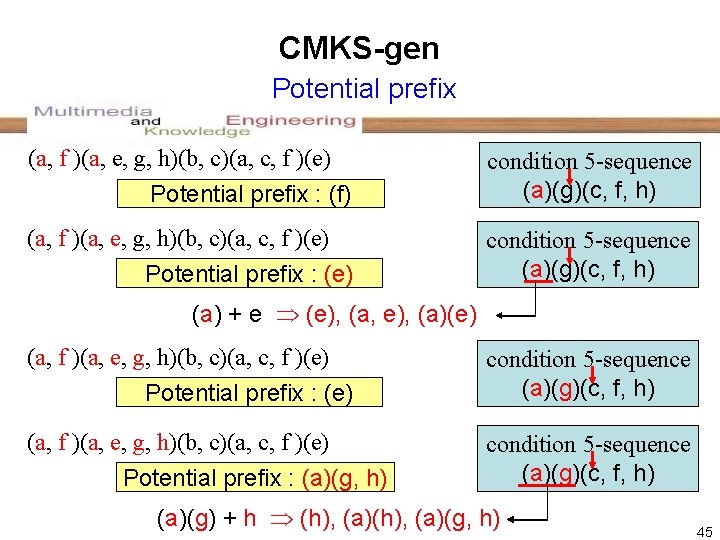
CMKS-gen Potential prefix (a, f )(a, e, g, h)(b, c)(a, c, f )(e) Potential prefix : (f) condition 5 -sequence (a)(g)(c, f, h) (a, f )(a, e, g, h)(b, c)(a, c, f )(e) Potential prefix : (e) condition 5 -sequence (a)(g)(c, f, h) (a) + e (e), (a, e), (a)(e) (a, f )(a, e, g, h)(b, c)(a, c, f )(e) Potential prefix : (e) condition 5 -sequence (a)(g)(c, f, h) (a, f )(a, e, g, h)(b, c)(a, c, f )(e) Potential prefix : (a)(g, h) condition 5 -sequence (a)(g)(c, f, h) (a)(g) + h (h), (a)(g, h) 45
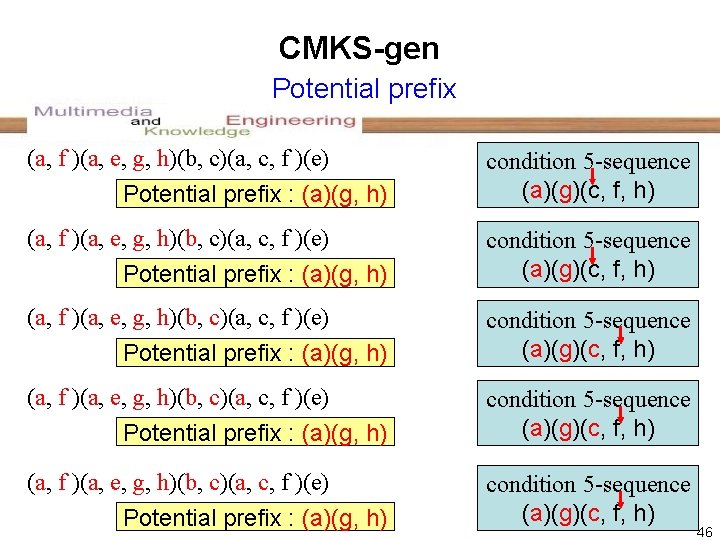
CMKS-gen Potential prefix (a, f )(a, e, g, h)(b, c)(a, c, f )(e) Potential prefix : (a)(g, h) condition 5 -sequence (a)(g)(c, f, h) (a, f )(a, e, g, h)(b, c)(a, c, f )(e) Potential prefix : (a)(g, h) condition 5 -sequence (a)(g)(c, f, h) 46
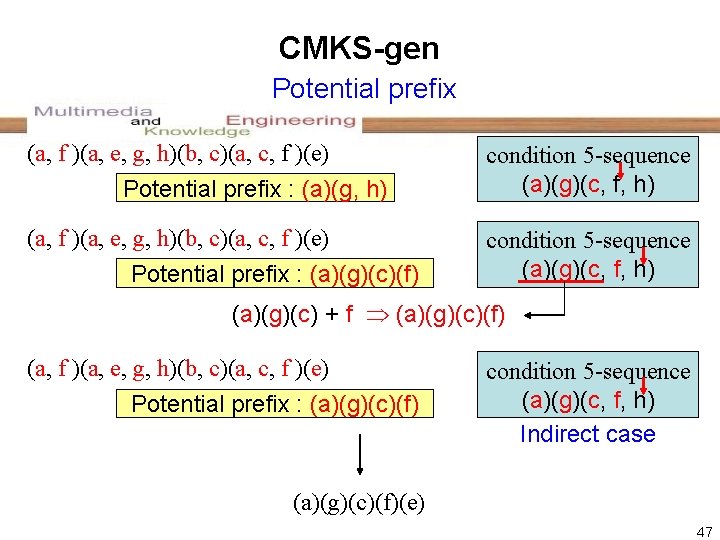
CMKS-gen Potential prefix (a, f )(a, e, g, h)(b, c)(a, c, f )(e) Potential prefix : (a)(g, h) condition 5 -sequence (a)(g)(c, f, h) (a, f )(a, e, g, h)(b, c)(a, c, f )(e) Potential prefix : (a)(g)(c)(f) condition 5 -sequence (a)(g)(c, f, h) (a)(g)(c) + f (a)(g)(c)(f) (a, f )(a, e, g, h)(b, c)(a, c, f )(e) Potential prefix : (a)(g)(c)(f) condition 5 -sequence (a)(g)(c, f, h) Indirect case (a)(g)(c)(f)(e) 47
Problems CID Customer sequence Minimum 3 -subsequence 1 (a, e, g)1 (b)2 (h)3 (f)4 (c)5 (b, f)6 (a)1 (b)2 (b)3 4 (f)1 (a, g)2 (b, f, h)3 (b, f)4 (a)1 (b)2 (b)3 How to find the minimum k-subsequence? 2 (b)1 (d, f)2 (e)3 (b)1 (d)2 (e)3 MKS-gen 3 (b, f, g)1 We generate the conditional minimum 3 -subsequence, which should be larger than or equal to <(b)(d)(e)>. <(a, e, g)(b)(h)(f)(c)(b, f)> <(b)(f)(b)> <(f)(a, g)(b, f, h)(b, f)> <(b, f)(b)> Locative AVL-tree How to support the efficient manipulation of the min-k ordered database? • sort, search How to find the conditional minimum k-subsequence? CMKS-gen 48
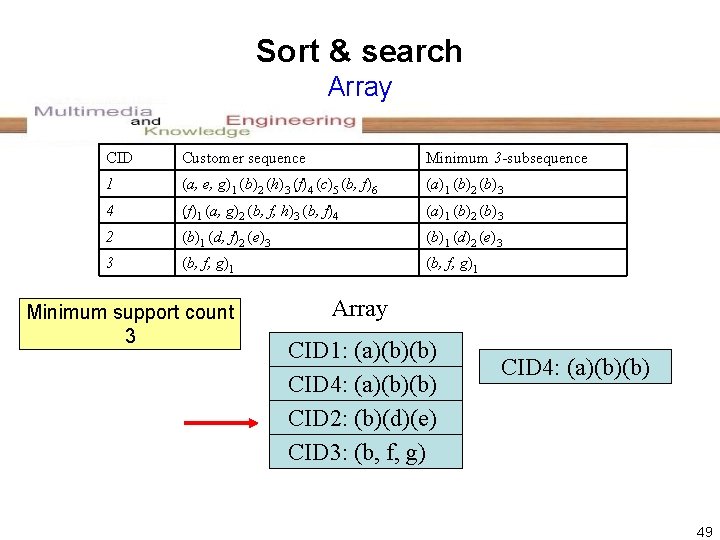
Sort & search Array CID Customer sequence Minimum 3 -subsequence 1 (a, e, g)1 (b)2 (h)3 (f)4 (c)5 (b, f)6 (a)1 (b)2 (b)3 4 (f)1 (a, g)2 (b, f, h)3 (b, f)4 (a)1 (b)2 (b)3 2 (b)1 (d, f)2 (e)3 (b)1 (d)2 (e)3 3 (b, f, g)1 Minimum support count 3 Array CID 1: (a)(b)(b) CID 2: (a)(b)(b) CID 4: (b)(d)(e) CID 3: (b)(d)(e) CID 2: (b, f, g) CID 3: (b, f, g) CID 4: (a)(b)(b) 49
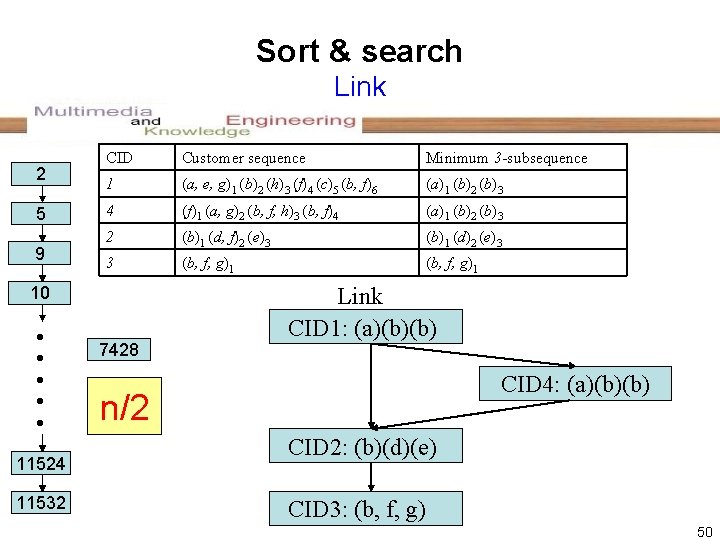
Sort & search Link 2 5 9 CID Customer sequence Minimum 3 -subsequence 1 (a, e, g)1 (b)2 (h)3 (f)4 (c)5 (b, f)6 (a)1 (b)2 (b)3 4 (f)1 (a, g)2 (b, f, h)3 (b, f)4 (a)1 (b)2 (b)3 2 (b)1 (d, f)2 (e)3 (b)1 (d)2 (e)3 3 (b, f, g)1 10 11524 11532 7428 Link CID 1: (a)(b)(b) CID 4: (a)(b)(b) n/2 CID 2: (b)(d)(e) CID 3: (b, f, g) 50
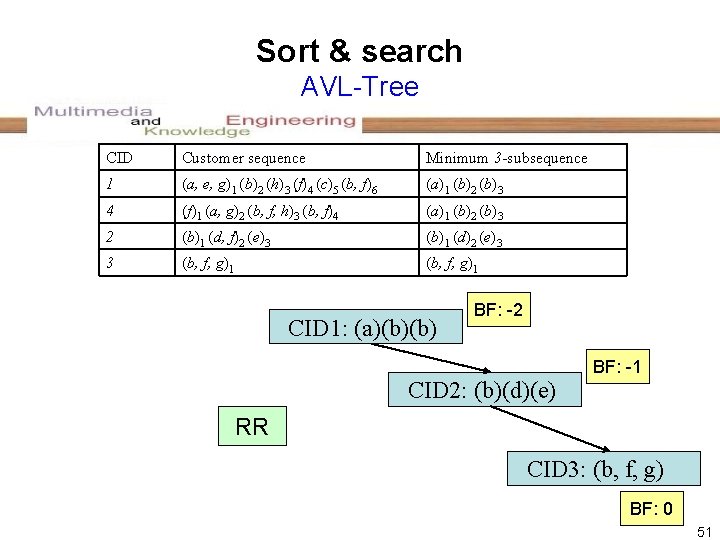
Sort & search AVL-Tree CID Customer sequence Minimum 3 -subsequence 1 (a, e, g)1 (b)2 (h)3 (f)4 (c)5 (b, f)6 (a)1 (b)2 (b)3 4 (f)1 (a, g)2 (b, f, h)3 (b, f)4 (a)1 (b)2 (b)3 2 (b)1 (d, f)2 (e)3 (b)1 (d)2 (e)3 3 (b, f, g)1 CID 1: (a)(b)(b) BF: 0 -1 -2 CID 2: (b)(d)(e) BF: -1 BF: 0 RR CID 3: (b, f, g) BF: 0 51
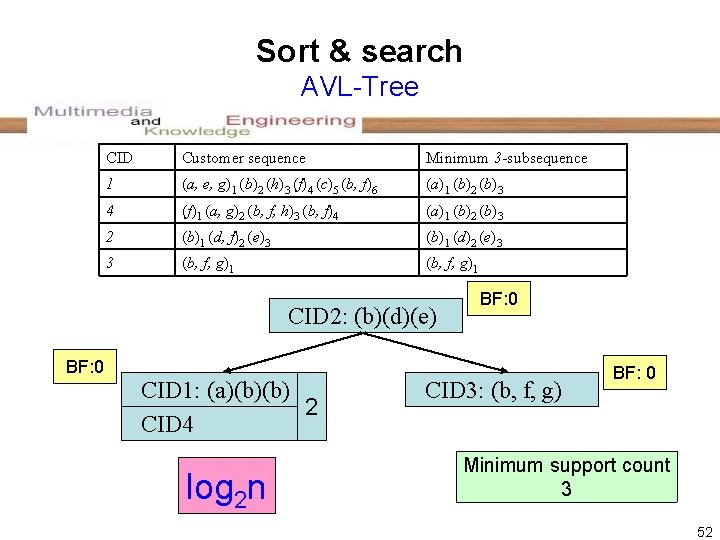
Sort & search AVL-Tree CID Customer sequence Minimum 3 -subsequence 1 (a, e, g)1 (b)2 (h)3 (f)4 (c)5 (b, f)6 (a)1 (b)2 (b)3 4 (f)1 (a, g)2 (b, f, h)3 (b, f)4 (a)1 (b)2 (b)3 2 (b)1 (d, f)2 (e)3 (b)1 (d)2 (e)3 3 (b, f, g)1 CID 2: (b)(d)(e) BF: 0 CID 1: (a)(b)(b) 2 CID 4 log 2 n BF: 0 CID 3: (b, f, g) BF: 0 Minimum support count 3 52
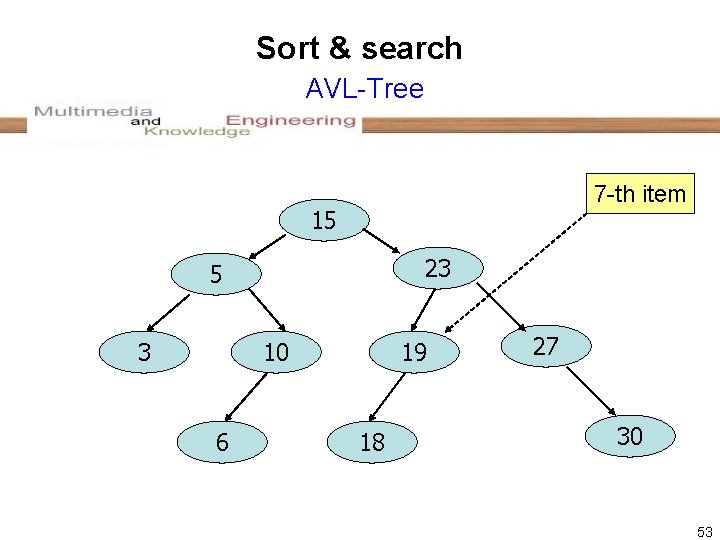
Sort & search AVL-Tree 7 -th item 15 23 5 3 10 6 19 18 27 30 53
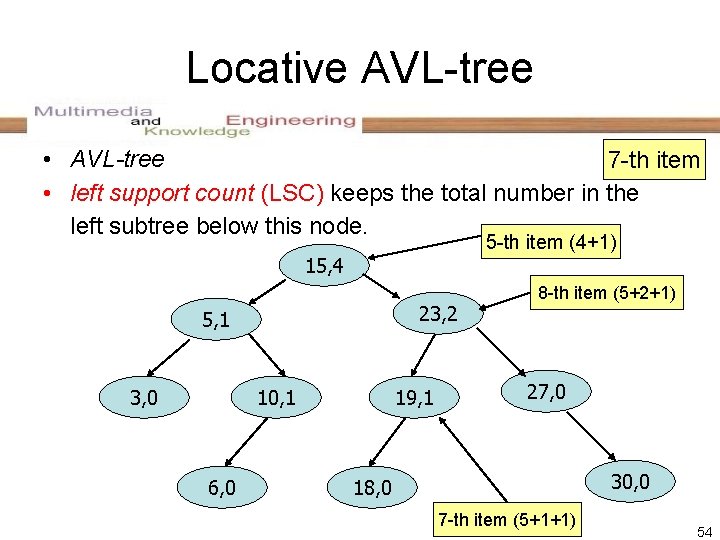
Locative AVL-tree • AVL-tree 7 -th item • left support count (LSC) keeps the total number in the left subtree below this node. 5 -th item (4+1) 15, 4 23, 2 5, 1 3, 0 10, 1 6, 0 19, 1 8 -th item (5+2+1) 27, 0 30, 0 18, 0 7 -th item (5+1+1) 54
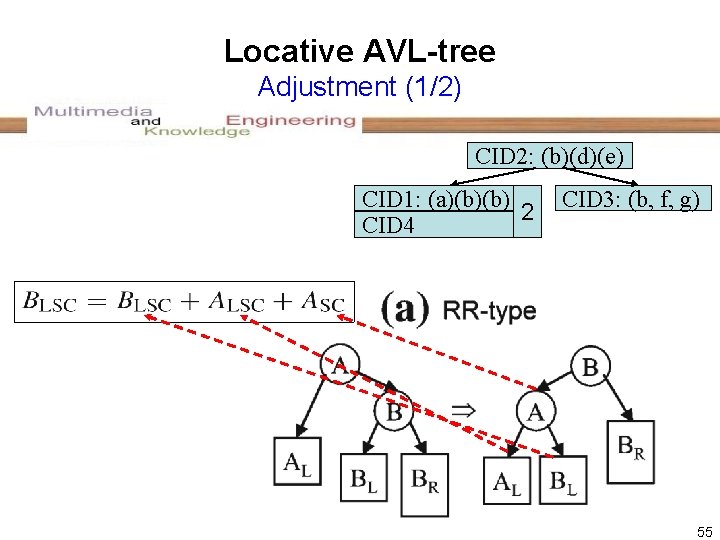
Locative AVL-tree Adjustment (1/2) CID 2: (b)(d)(e) CID 1: (a)(b)(b) 2 CID 4 CID 3: (b, f, g) 55
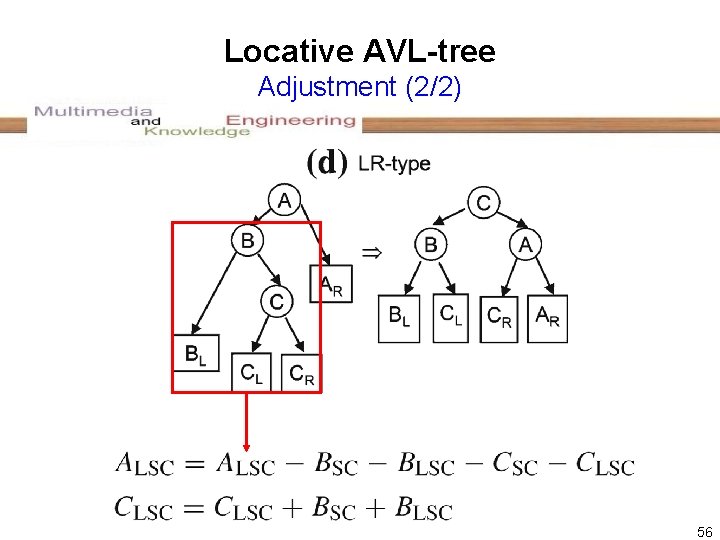
Locative AVL-tree Adjustment (2/2) 56
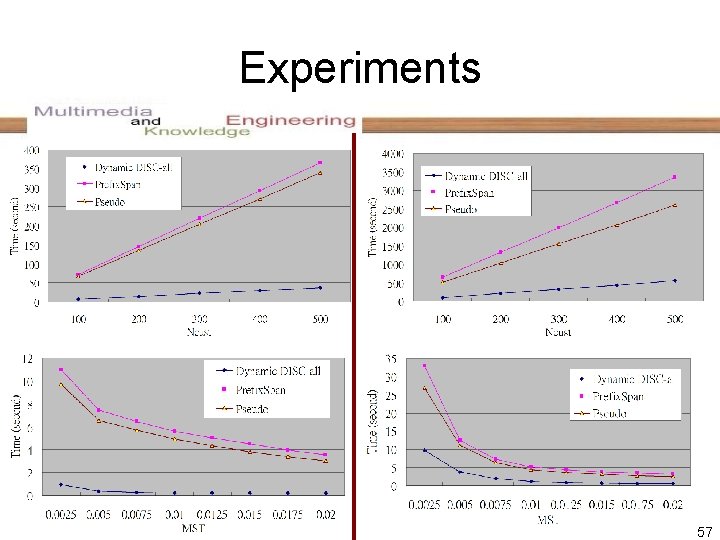
Experiments 57
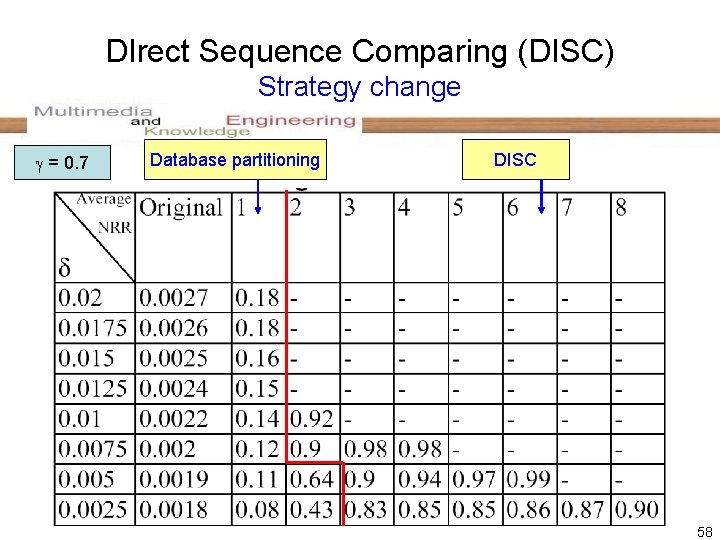
DIrect Sequence Comparing (DISC) Strategy change = 0. 7 Database partitioning DISC 58
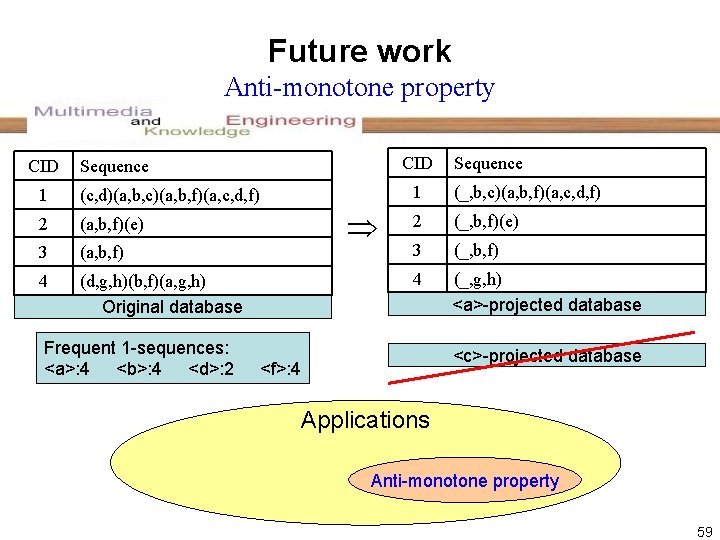
Future work Anti-monotone property CID Sequence 1 (c, d)(a, b, c)(a, b, f)(a, c, d, f) 2 (a, b, f)(e) 3 (a, b, f) 4 (d, g, h)(b, f)(a, g, h) Original database Frequent 1 -sequences: <a>: 4 <b>: 4 <d>: 2 Sequence 1 (_, b, c)(a, b, f)(a, c, d, f) 2 (_, b, f)(e) 3 (_, b, f) 4 (_, g, h) <a>-projected database <c>-projected database <f>: 4 Applications Anti-monotone property 59

Future work Mining profitable sequences • DISC strategy can be applied to the problems without the antimonotone property. • Profitable sequences – The sequence profit of <(a)1(b)2> is 90. – The support profit of <(a)1(b)2> is 180 since its support count is 2 and its sequence profit is 90. – The support profit of <(a)1(b, e)2> is 240 because its support count is 2 and its sequence profit becomes 120. minimum support profit = 200 60

Future work Mining profitable sequences • Example minimum support profit = 400 – The sequence profit of <(a)1(a, b, c)2> is 180. – The minimum required count of <(a)1(a, b, c)2> is 3. 61
- Slides: 61