Frequency Distributions Histograms Percentiles and Percentile Ranks and

Frequency Distributions, Histograms, Percentiles and Percentile Ranks and their Graphical Representations

Chapter 2: Frequency Distributions, Histograms, Percentiles and Percentile Ranks How can we represent or summarize a list of values? frequency distribution: shows the number of observations for the possible categories or score values in a set of data. Can be done on any scale (nominal, ordinal, interval, or ratio). Often represented as a bar graph. Example of a frequency distribution for nominal scale data: 2008 Auto sales by country: Japan: 11, 563, 629 China: 9, 345, 101 US: 8, 705, 239 Germany: 6, 040, 582 South Korea: 3, 806, 682 Brazil: 3, 220, 475

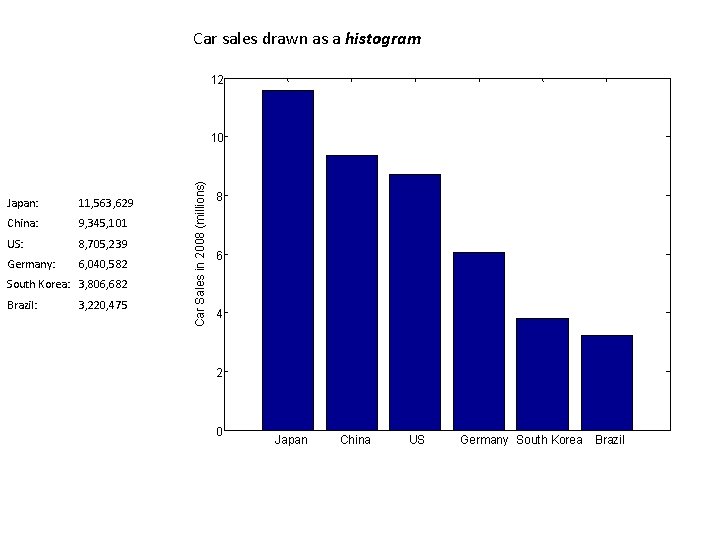
Car sales drawn as a histogram 12 Japan: 11, 563, 629 China: 9, 345, 101 US: 8, 705, 239 Germany: 6, 040, 582 South Korea: 3, 806, 682 Brazil: 3, 220, 475 Car Sales in 2008 (millions) 10 8 6 4 2 0 Japan China US Germany South Korea Brazil

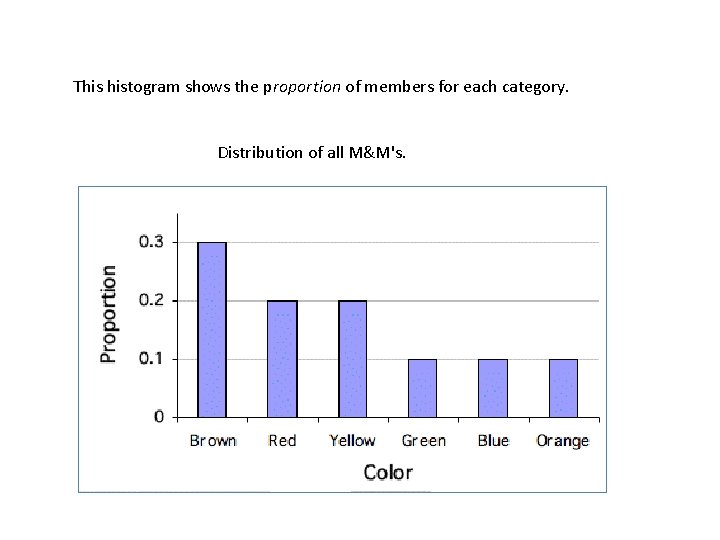
This histogram shows the proportion of members for each category. Distribution of all M&M's.

Here are 20 final grade scores for a class of 20 students: How can we describe and visualize this set of numbers? If we were to grade on a curve, how do we decide where the cutoffs are?

Making histograms from interval and ratio data Example data: test scores from a class of 20 students. We need to bin the raw scores into a set of class intervals. How do we decide these class intervals? Be sure the intervals don’t overlap, have the same width, and cover the entire range of scores. Use around 10 to 20 intervals. Use a sensible width (like 5, and not 2. 718285) Make the lower score a multiple of the width (e. g. if the width is 5, a lower score should be 50, not 48) If a score lands on the border, put it in the lower class interval.

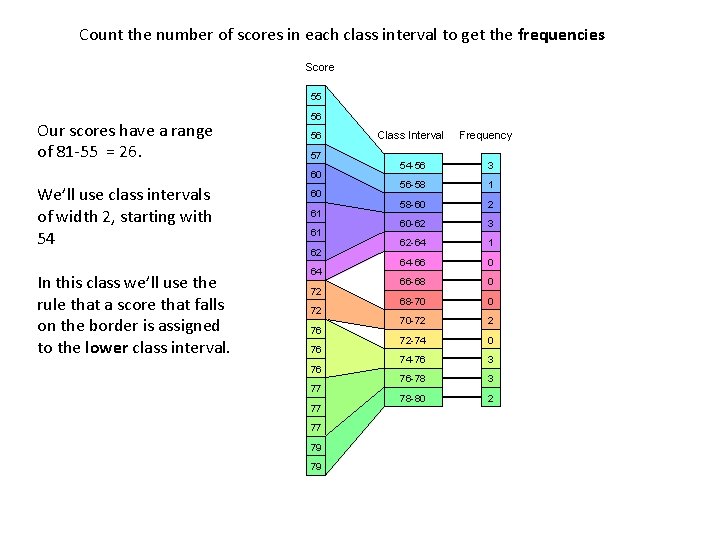
Count the number of scores in each class interval to get the frequencies Score 55 Our scores have a range of 81 -55 = 26. 56 56 57 60 We’ll use class intervals of width 2, starting with 54 In this class we’ll use the rule that a score that falls on the border is assigned to the lower class interval. 60 61 61 62 64 72 72 76 76 76 77 77 77 79 79 Class Interval Frequency 54 -56 3 56 -58 1 58 -60 2 60 -62 3 62 -64 1 64 -66 0 66 -68 0 68 -70 0 70 -72 2 72 -74 0 74 -76 3 76 -78 3 78 -80 2

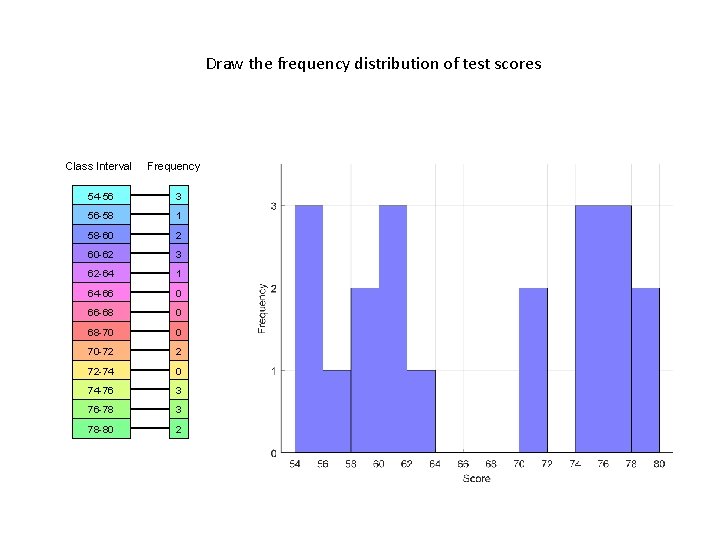
Draw the frequency distribution of test scores Class Interval Frequency 54 -56 3 56 -58 1 58 -60 2 60 -62 3 62 -64 1 64 -66 0 66 -68 0 68 -70 0 70 -72 2 72 -74 0 74 -76 3 76 -78 3 78 -80 2

Relative frequency: the percent of scores that fall in each class interval. Divide by the total number of scores to get relative frequency in proportion Then multiply by 100 to get relative frequency in percent (100)(3)/20 = 15

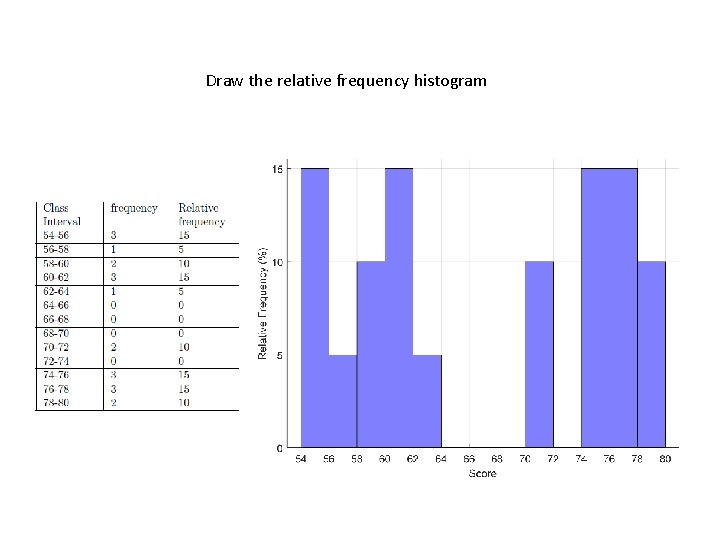
Draw the relative frequency histogram

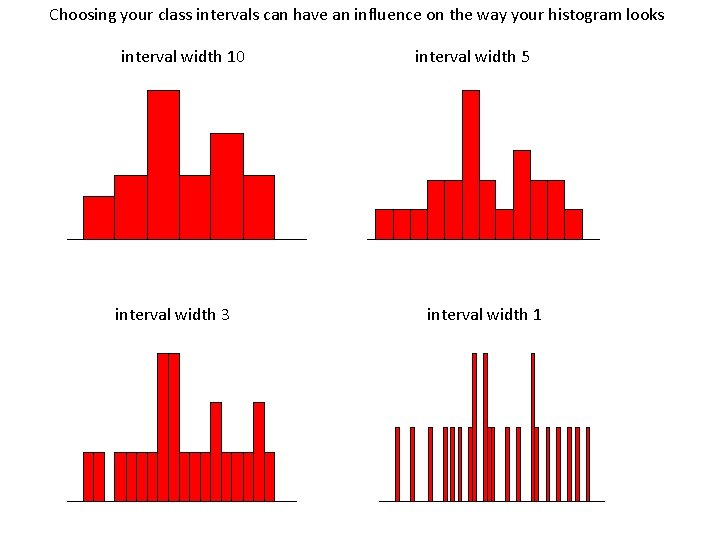
Choosing your class intervals can have an influence on the way your histogram looks interval width 10 interval width 5 5 Frequency 7 6 5 4 3 2 1 0 4 3 2 1 60 70 80 90 100 110 120 Ice Dancing Score 0 60 interval width 3 interval width 1 2 Frequency 3 2 1 0 80 100 Ice Dancing Score 60 80 100 Ice Dancing Score 1 0 60 80 100 Ice Dancing Score

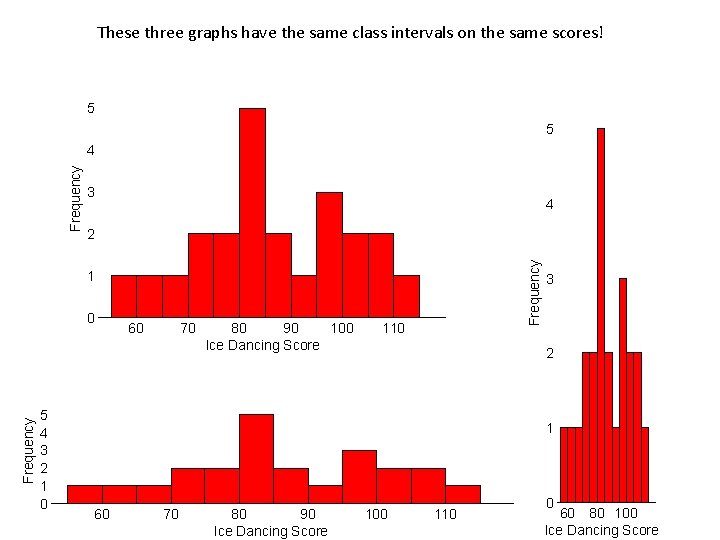
These three graphs have the same class intervals on the same scores! 5 5 3 4 2 Frequency 4 1 Frequency 0 5 4 3 2 1 0 60 70 80 90 100 Ice Dancing Score 110 3 2 1 60 70 80 90 Ice Dancing Score 100 110 0 60 80 100 Ice Dancing Score

When possible, include zero on your y-axis. Not like this

To be fair (and balanced), Fox News soon apologized and corrected its ‘mistake‘

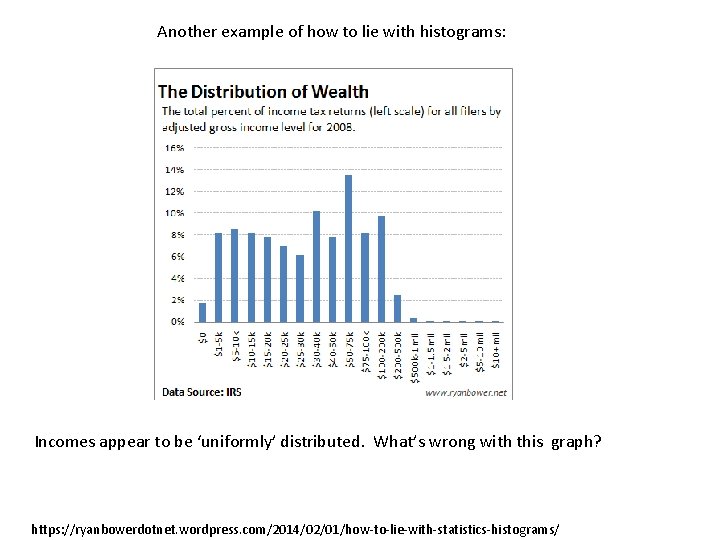
Another example of how to lie with histograms: Incomes appear to be ‘uniformly’ distributed. What’s wrong with this graph? https: //ryanbowerdotnet. wordpress. com/2014/02/01/how-to-lie-with-statistics-histograms/

Percentile ranks and percentile points: Percentile Point: A point on the measurement scale below which a specific percentage of scores fall. Percentile Rank: The percentage of cases that fall below a given point on the measurement scale. Percentile ranks are always between zero and 100.

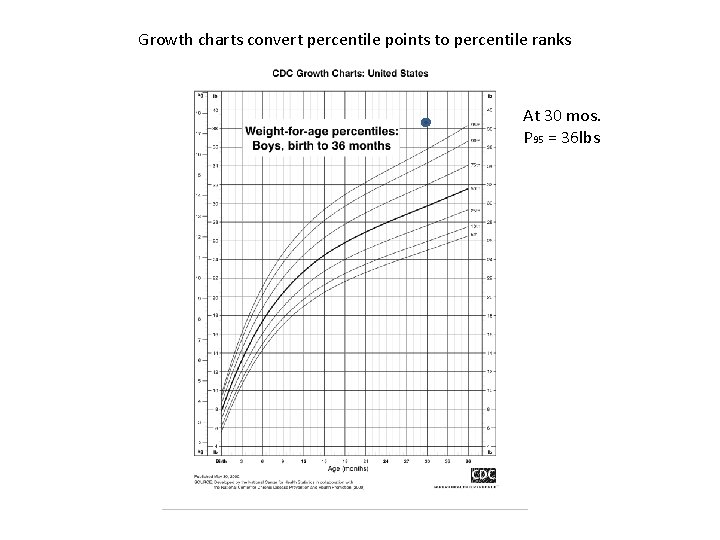
Growth charts convert percentile points to percentile ranks At 30 mos. P 95 = 36 lbs

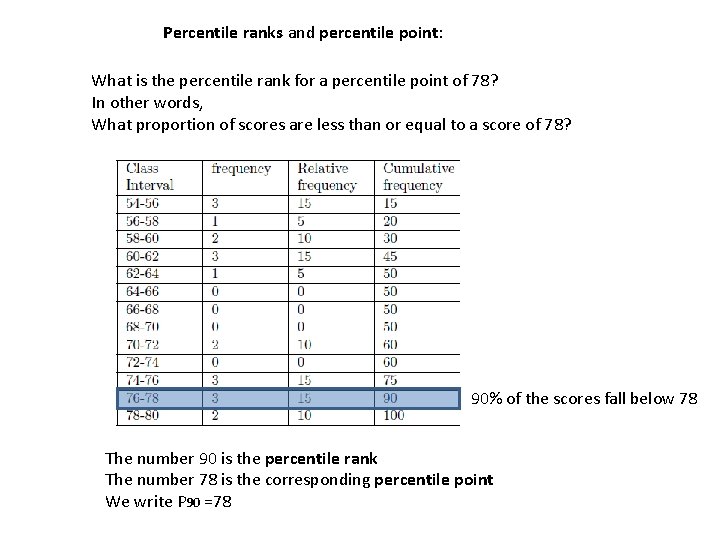
Percentile ranks and percentile point: What is the percentile rank for a percentile point of 78? In other words, What proportion of scores are less than or equal to a score of 78? 90% of the scores fall below 78 The number 90 is the percentile rank The number 78 is the corresponding percentile point We write P 90 =78

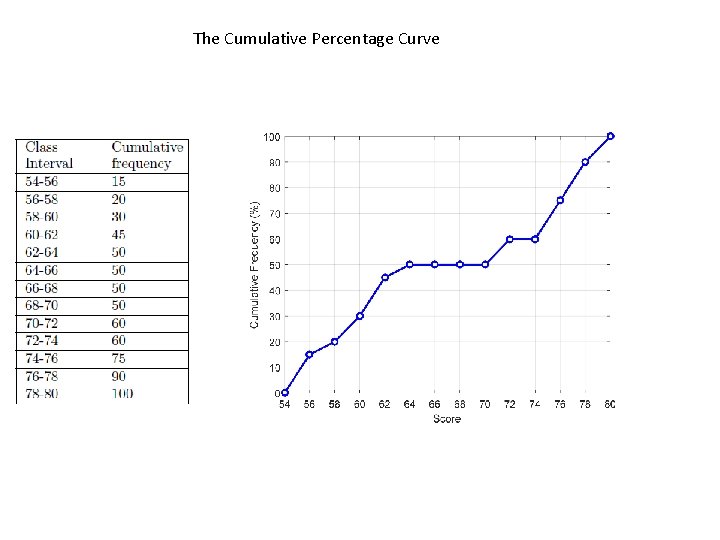
The Cumulative Percentage Curve

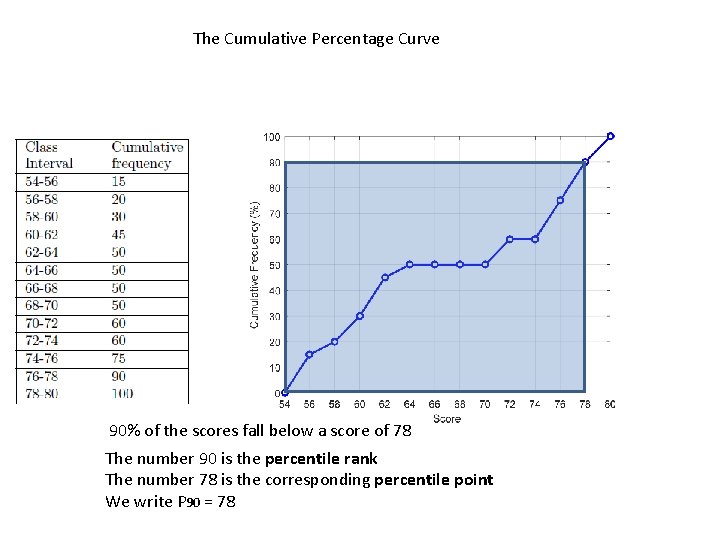
The Cumulative Percentage Curve 90% of the scores fall below a score of 78 The number 90 is the percentile rank The number 78 is the corresponding percentile point We write P 90 = 78

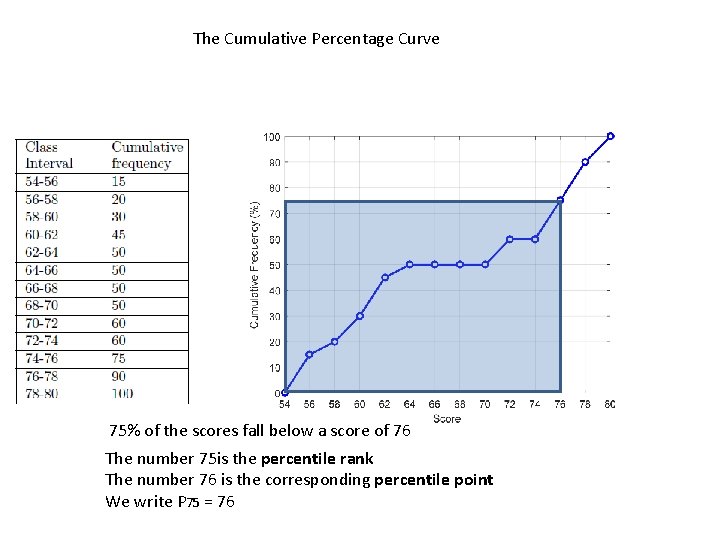
The Cumulative Percentage Curve 75% of the scores fall below a score of 76 The number 75 is the percentile rank The number 76 is the corresponding percentile point We write P 75 = 76

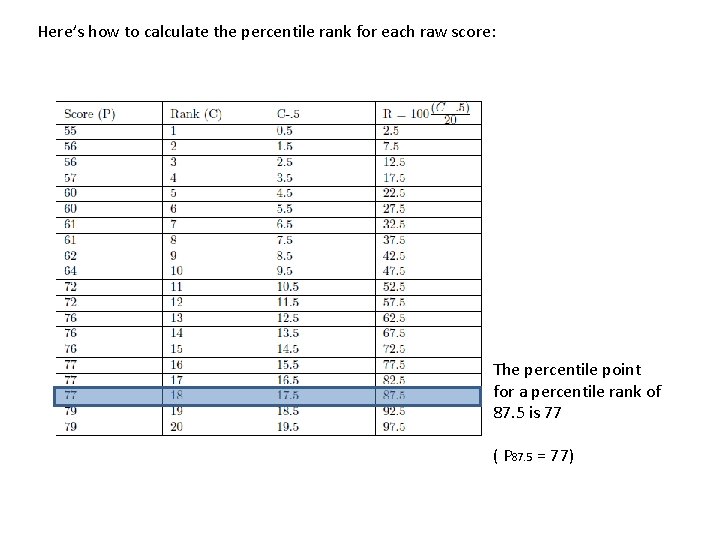
Here’s how to calculate the percentile rank for each raw score: The percentile point for a percentile rank of 87. 5 is 77 ( P 87. 5 = 77)

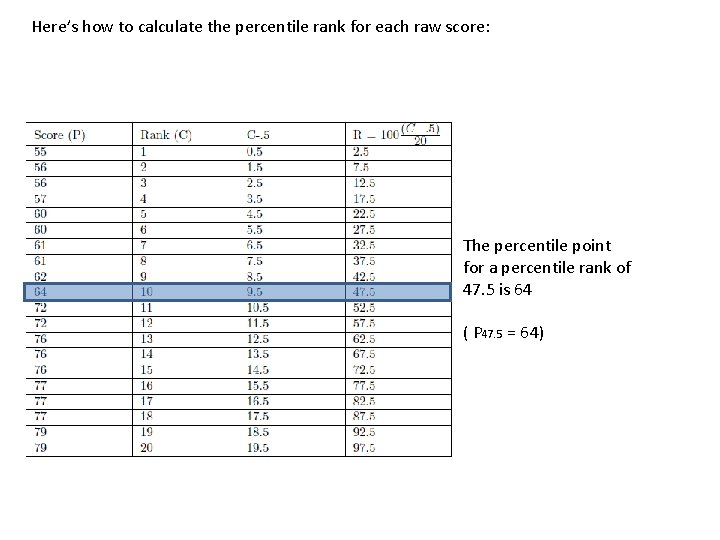
Here’s how to calculate the percentile rank for each raw score: The percentile point for a percentile rank of 47. 5 is 64 ( P 47. 5 = 64)

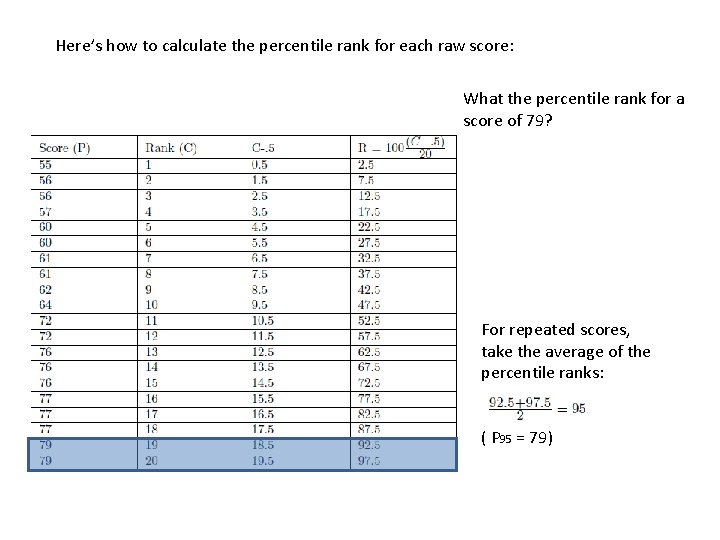
Here’s how to calculate the percentile rank for each raw score: What the percentile rank for a score of 79? For repeated scores, take the average of the percentile ranks: ( P 95 = 79)

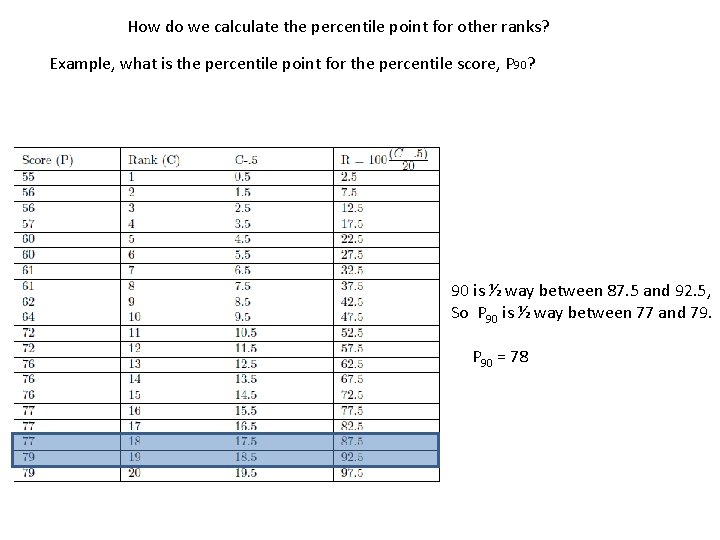
How do we calculate the percentile point for other ranks? Example, what is the percentile point for the percentile score, P 90? 90 is ½ way between 87. 5 and 92. 5, So P 90 is ½ way between 77 and 79. P 90 = 78

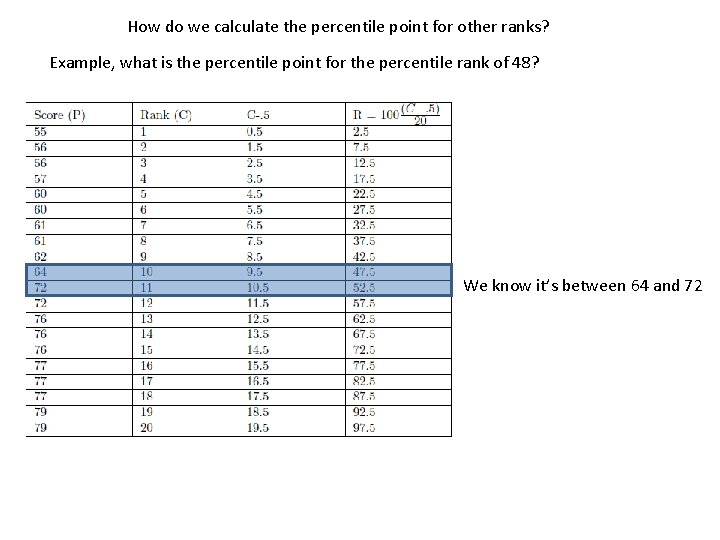
How do we calculate the percentile point for other ranks? Example, what is the percentile point for the percentile rank of 48? We know it’s between 64 and 72

Linear Interpolation for calculating percentile points: Example, what is the percentile point for the percentile rank of 48? 1) 2) 3) 4) 5) Make a chart like the one above Find the two rows that fall above and below the percentile rank Let RL and RH be the high and low percentile ranks (47. 5 and 52. 5 in this example) Let PL and PH be the high and low percentile points (64 and 72 in this example) If R is the percentile rank (48 in our example), then the percentile point is: P 48 = 64. 8

Going the other way: from percentile ranks to percentile points Example: What is the percentile rank for the percentile point of 78? We know that it is between 87. 5 and 92. 5. PL = 77, PH = 79, RL= 87. 5, RH = 92. 5 If P=78 is the percentile point, then the percentile rank is: P 90 = 78

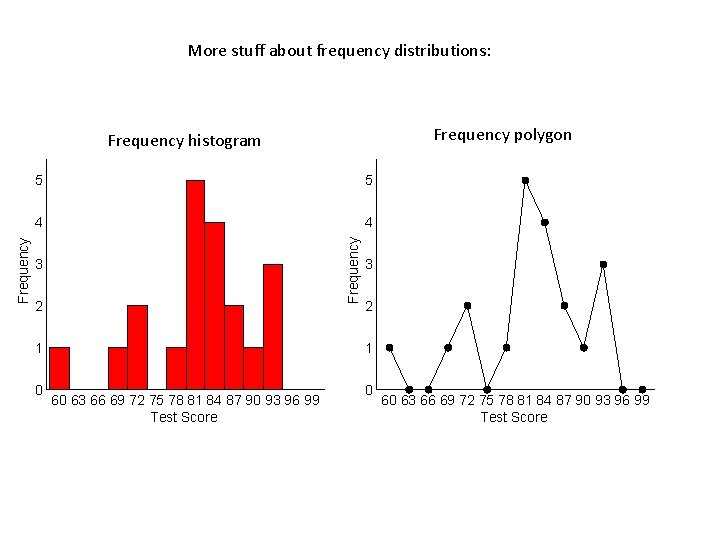
More stuff about frequency distributions: Frequency polygon 5 5 4 4 Frequency histogram 3 2 1 0 3 2 1 60 63 66 69 72 75 78 81 84 87 90 93 96 99 Test Score 0 60 63 66 69 72 75 78 81 84 87 90 93 96 99 Test Score

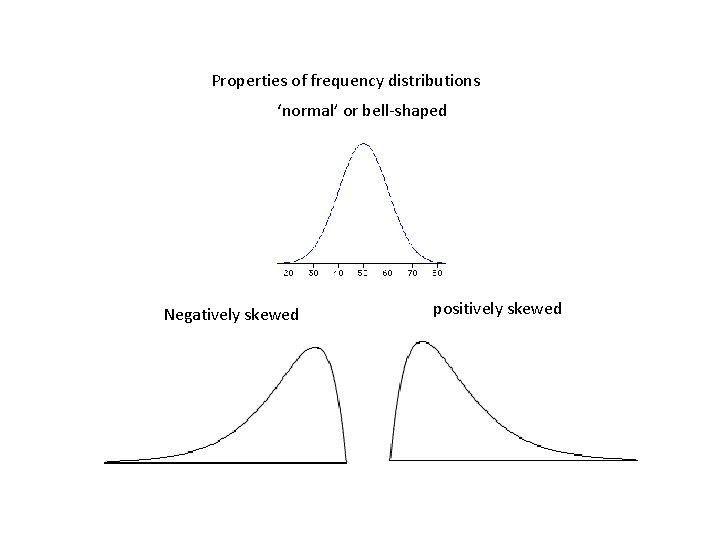
Properties of frequency distributions ‘normal’ or bell-shaped Negatively skewed positively skewed

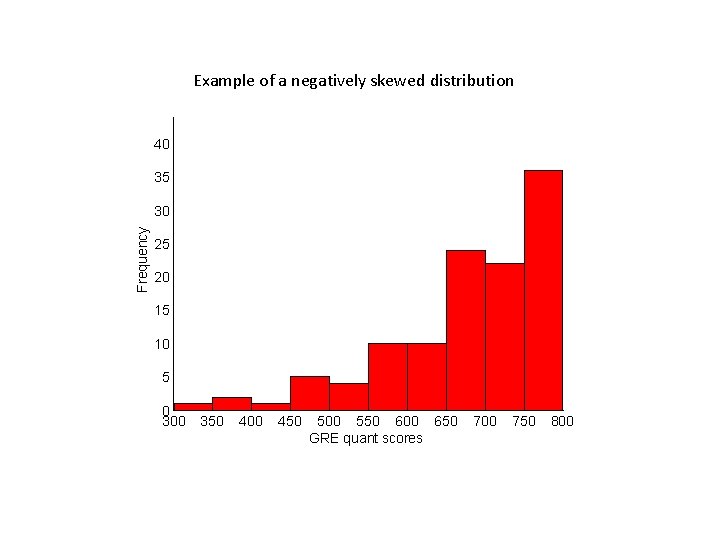
Example of a negatively skewed distribution 40 35 Frequency 30 25 20 15 10 5 0 300 350 400 450 500 550 600 650 GRE quant scores 700 750 800

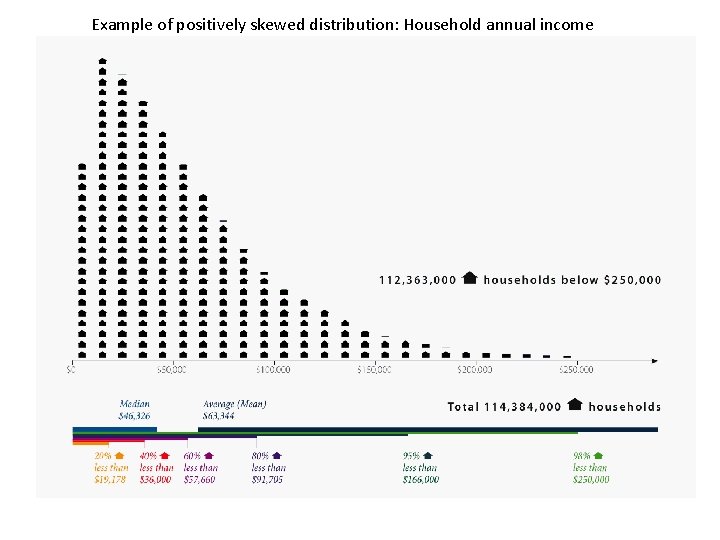
Example of positively skewed distribution: Household annual income

Household income distribution as of 2006: • P 0 -89 (bottom 90%) — income below $104, 696 (average income, $30, 374*) • P 90 -100 (top 10%) — income above $104, 696 (average income, $269, 658*) • P 90 -95 (next 5%) — income between $104, 696 and $148, 423 (average income, $122, 429*) • P 95 -99 (next 4%) — income between $148, 423 and $382, 593 (average income, $210, 597*) • P 99 -100 (top 1%) — income above $382, 593 (average income, $1, 243, 516*) • P 99. 5 -100 (top 0. 5%) — income above $597, 584 (average income, $2, 022, 315*) • P 99. 9 -100 (top 0. 1%) — income above $1, 898, 200 (average income, $6, 289, 800*) • P 99. 99 -100 (top. 01%) —income above $10, 659, 283 (average income, $29, 638, 027*) So the ‘top 1%’ can be described as: P 99 = $382, 593 http: //www. wealthandwant. com/issues/income_distribution. html

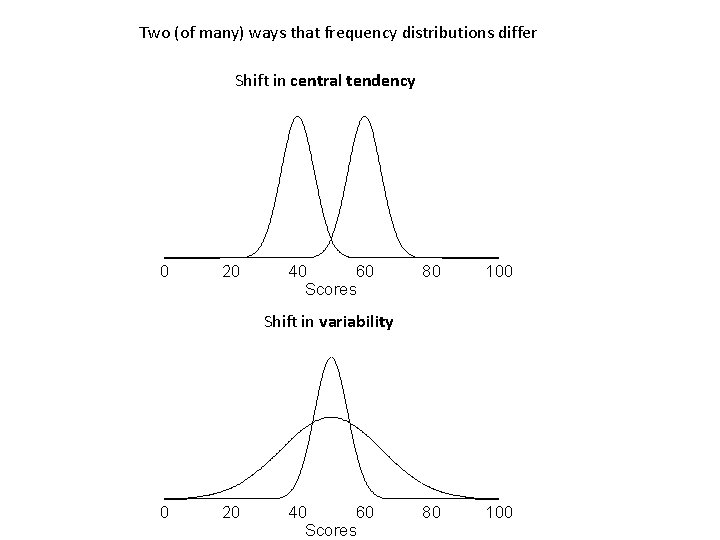
Two (of many) ways that frequency distributions differ Shift in central tendency 0 20 40 60 Scores 80 100 Shift in variability 0 20 40 60 Scores