Frelsning 6 Semantik Statisk semantik Attributgrammatiker Dynamisk semantik

Föreläsning 6: Semantik • • Statisk semantik Attributgrammatiker Dynamisk semantik Axiomatisk semantik: inferensregler och korrekthetsbevis 2002 -11 -19 F. Drewes, Inst. f. datavetenskap 1

Statisk semantik • Semantik = programmens betydelse • Statisk semantik = semantiska aspekter som inte direkt har att göra med programmets exekvering Ø oftast frågor i samband med deklarationer: typisering, (icke) deklarerade identifierare, … Ø innefattar ”icke kontextfri syntax” Typisering i Java: Namnupprepning i Ada: int i; procedure p is i = 3. 3; // typfel! end q; -- fel namn! 2002 -11 -19 F. Drewes, Inst. f. datavetenskap 2

Attributgrammatiker (Knuth 1968) är används ofta för att beskriva statisk semantik men kan t. o. m. användas för att översätta program helt och hållet. Idé: Deriveringsträdets noder förses med attribut • varje attribut har ett värde (tal, sträng, graf, …) • värdet beror på Ø förälderns och syskonens attributvärden (ärvt attribut) eller Ø barnens attributvärden (syntetiserat attribut) • attributvärden utvärderas rekursivt 2002 -11 -19 F. Drewes, Inst. f. datavetenskap 3

Attributgrammatiker (2) Typer av attribut i överblick • Syntetiserat Ø värde beror på barnens attributvärden informationsflöde uppåt • Ärvt Ø värde beror på förälderns och syskonens attributvärden informationsflöde nedåt • Inneboende (eng. intrinsic) Ø syntetiserade attribut på trädens löv som är definierade ”på något annat ställe än i attributgrammatiken” Ø finns inte i ”rena” attributgrammatiker 2002 -11 -19 F. Drewes, Inst. f. datavetenskap 4

Attributgrammatiker – exempel Attribut: ´expected´ typen som ett uttryck väntas ha (ärvt) ´actual´ typen som ett uttryck faktiskt har (syntetiserat) ´type´ variablens typ enligt deklarationen (inneboende) syntaktiska regler semantiska regler assign var = expr. expected = var. type expr 0 expr 1 + expr 2 expr i. expected = expr 0. expected där i {1, 2} expr 0. actual = int om expr 1. actual expr 2. actual int = real annars expr integer expr. actual = int expr real expr. actual = real expr var expr. actual = var. type Krav: expr 0. actual expr 0. expected 2002 -11 -19 F. Drewes, Inst. f. datavetenskap 5

Dynamisk semantik • Dynamisk semantik är den delen av semantiken som är nära relaterad till programexekveringen • Det finns många sätt att definiera den dynamiska semantiken för ett programspråk, bl a Ø operationell semantik Ø denotationell semantik Ø axiomatisk semantik 2002 -11 -19 läs om dem i boken! F. Drewes, Inst. f. datavetenskap 6

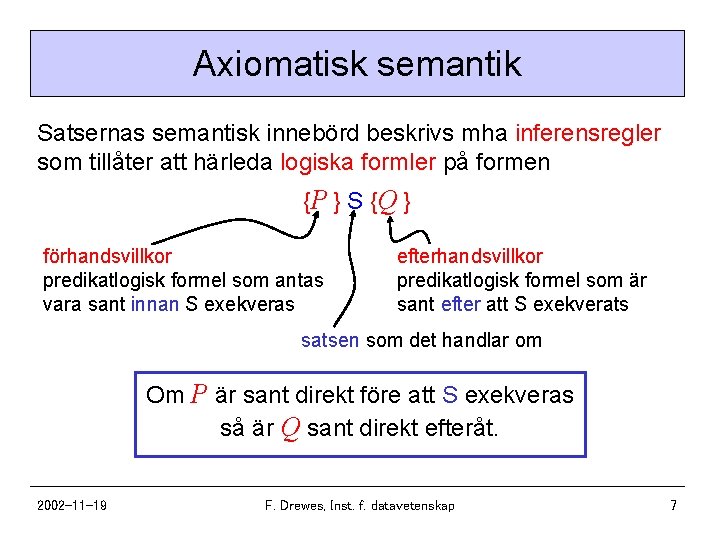
Axiomatisk semantik Satsernas semantisk innebörd beskrivs mha inferensregler som tillåter att härleda logiska formler på formen {P } S {Q } förhandsvillkor predikatlogisk formel som antas vara sant innan S exekveras efterhandsvillkor predikatlogisk formel som är sant efter att S exekverats satsen som det handlar om Om P är sant direkt före att S exekveras så är Q sant direkt efteråt. 2002 -11 -19 F. Drewes, Inst. f. datavetenskap 7

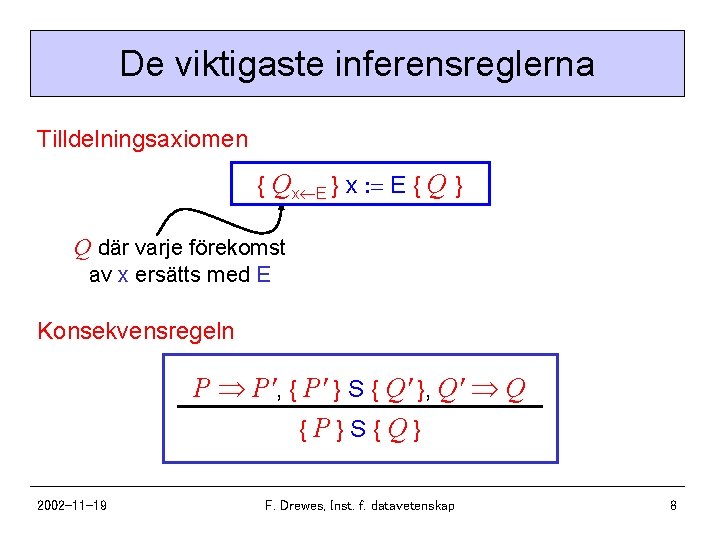
De viktigaste inferensreglerna Tilldelningsaxiomen { Qx E } x : E { Q } Q där varje förekomst av x ersätts med E Konsekvensregeln P P', { P' } S { Q' }, Q' Q { P} S { Q} 2002 -11 -19 F. Drewes, Inst. f. datavetenskap 8

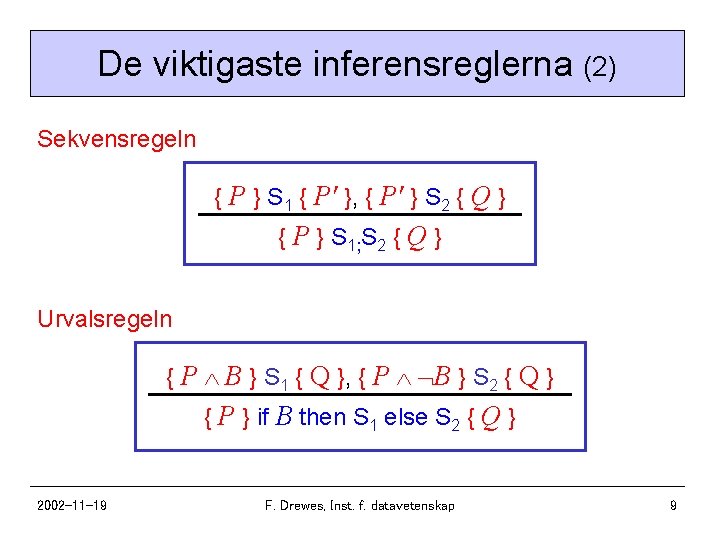
De viktigaste inferensreglerna (2) Sekvensregeln { P } S 1 { P' }, { P' } S 2 { Q } { P } S 1; S 2 { Q } Urvalsregeln { P B } S 1 { Q }, { P B } S 2 { Q } { P } if B then S 1 else S 2 { Q } 2002 -11 -19 F. Drewes, Inst. f. datavetenskap 9

De viktigaste inferensreglerna Loopregeln (endast partiell korrekthet) {B I}S{I} { I } while B do S end { B I } • loopinvarianten I är sant såväl före som efter varje exekvering av S • invarianten brukar beskriva förhållandet mellan variablerna som förekommer i S • total korrekthet = partiell korrekthet + loopen kommer att stanna 2002 -11 -19 F. Drewes, Inst. f. datavetenskap 10

Ett korrekthetsbevis {x 0} a : 0; {x 0 a 0} b : 0; {x 0 a b 0} while b x do tilldelningsaxiom (+konsekvensregel) {b x a b y} I {b x a b y} B I a : a + y; {b+ x 1 a x – ya b(b +y 1) } y} b : b + 1 {b x a b y} I end (b {b x x)a bb yx } a b y } B I {a=x y} 2002 -11 -19 F. Drewes, Inst. f. datavetenskap 11