Freestyle sculpting meshes with selfadaptive topology Lucian Stanculescu

Contents 1. Introduction 2. Quasi-uniform mesh 3. Time evolution 4. Sculpting tools 5. Results

1. Introduction - Goal : Develop an intuitive sculpting system • professional artists and

1. Introduction : : related work - Grid-based methods (Galyean and Hughes ‘ 91)

1. Introduction : : objective Enable topological changes in mesh models • Interactive Why

2. Quasi-uniform mesh Main idea : manifold mesh with uniform sampling Advantages : •

2. Quasi-uniform mesh : : detail D 1. Δ tight mesh – closed manifold

2. Quasi-uniform mesh : : mesh quality D 2. Compliance with d • iterate

2. Quasi-uniform mesh D 3. Quasi-uniform mesh • d < Δ , closed manifold

3. Time evolution Vertices displaced by deformation fields • Apply compliance with d •

3. Time evolution D 4. Θ : minimum thickness supported by quasi-uniform mesh Θ

3. Time evolution D 5. μ : maximum allowed displacement for a vertex. 4μ²≤Θ²-Δ²/3

3. Time evolution Difficulty : maintain manifold mesh Neighbourhood cleanup Handle degenerate cases •

4. Sculpting tools Displacement fields • Space deformations volume preserving • Model dependent normals,

4. Sculpting tools : : space Sweep deform (volume preserving) Freestyle

4. Sculpting tools : : model Inflate (normals) Freestyle

5. Results Object : 30 k points Collision detection – most time expensive GPU

6. Conclusions Handle arbitrary changes in topology simple quasi-uniform framework Intuitive model based on

6. Future work • Sharp features • Sculpting curves • Fast approximate Boolean operations

Slides: 21

Download presentation

Freestyle sculpting meshes with self-adaptive topology Lucian Stanculescu a, b , Raphaëlle Chaine a , Marie-Paule Cani b, c LIRIS, University of Lyon, France b LJK, University of Grenoble, France c INRIA, France a Freestyle

Contents 1. Introduction 2. Quasi-uniform mesh 3. Time evolution 4. Sculpting tools 5. Results 6. Conclusion and future work 7. Demo Freestyle

1. Introduction - Goal : Develop an intuitive sculpting system • professional artists and amateur users - Digital sculpting : important tool for 3 D content creation • animated movies, special effects, computer games - Models behind professional applications : • polygonal (no changes in topological genus) • ZBrush, Mudbox, Sculptris, Blender • regular grids (surface extraction, no color) • 3 D Coat - Specific workflow • limitations Freestyle

1. Introduction : : related work - Grid-based methods (Galyean and Hughes ‘ 91) • • Deformation tools (Ferley et al. ‘ 01), virtual clay (Dewaele et al. ‘ 04) Surface extraction - Implicit methods : Blob Tree • • Deformations by Warp Curves (Sugihara et al. ‘ 10) Hierarchy of tools - Particle systems (Pons and Boissonnat ‘ 07, Debard et al. ‘ 07) • topology changes, quality adaptive mesh – relaxation process slow - Mesh-based • • • Model-based deformations : Laplacian editing (Sorkine et al. ‘ 04) Space deformations (Angelidis et al. ‘ 04, von Funck et al. ‘ 06) No change in topology Freestyle

1. Introduction : : objective Enable topological changes in mesh models • Interactive Why meshes ? • No relaxation and complex reconstruction • Large variety of tools • Fast rendering on GPU Freestyle

2. Quasi-uniform mesh Main idea : manifold mesh with uniform sampling Advantages : • Simplify collision detection • Easily handle changes in topology • Simple tracking of surface deformations Freestyle

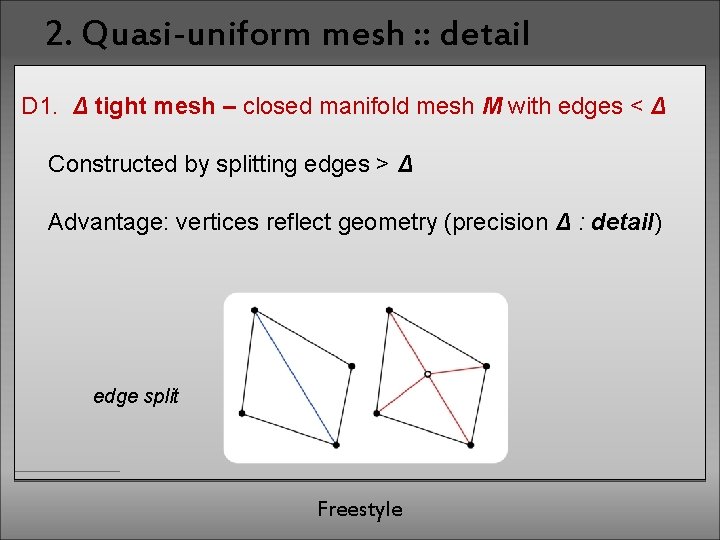
2. Quasi-uniform mesh : : detail D 1. Δ tight mesh – closed manifold mesh M with edges < Δ Constructed by splitting edges > Δ Advantage: vertices reflect geometry (precision Δ : detail) edge split Freestyle

2. Quasi-uniform mesh : : mesh quality D 2. Compliance with d • iterate over all edges • collapse if edge < d ! Favored for most edges but not guaranteed edge collapse Freestyle

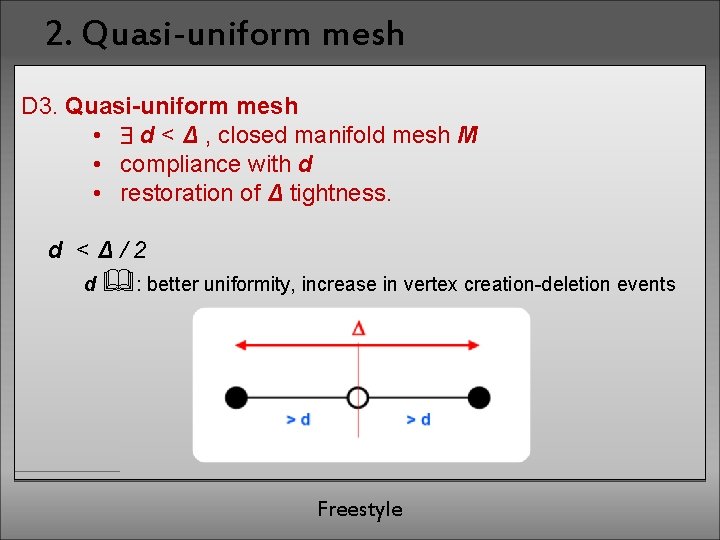
2. Quasi-uniform mesh D 3. Quasi-uniform mesh • d < Δ , closed manifold mesh M • compliance with d • restoration of Δ tightness. d <Δ/2 d : better uniformity, increase in vertex creation-deletion events Freestyle

3. Time evolution Vertices displaced by deformation fields • Apply compliance with d • Restore Δ tightness • Handle topology Difficulty Detect important events before : • Loss in detail • Self-intersection Freestyle

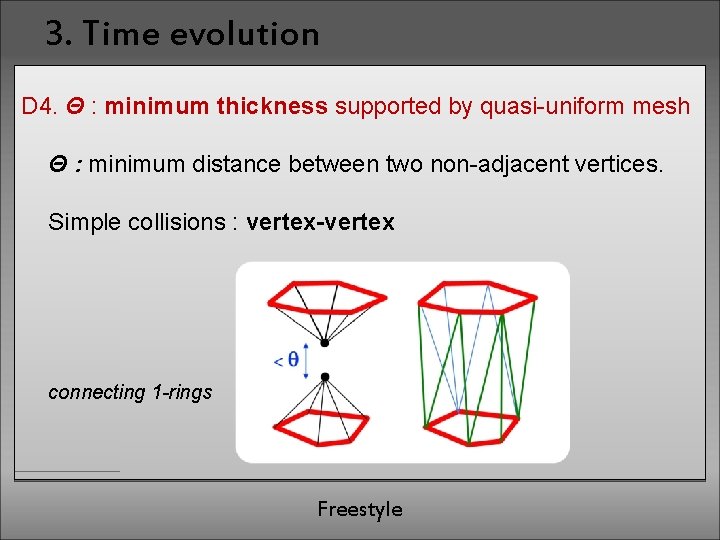
3. Time evolution D 4. Θ : minimum thickness supported by quasi-uniform mesh Θ : minimum distance between two non-adjacent vertices. Simple collisions : vertex-vertex connecting 1 -rings Freestyle

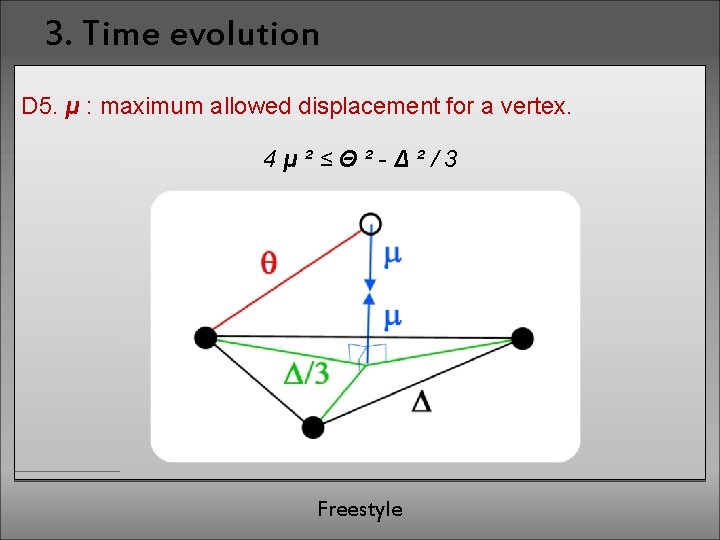
3. Time evolution D 5. μ : maximum allowed displacement for a vertex. 4μ²≤Θ²-Δ²/3 Freestyle

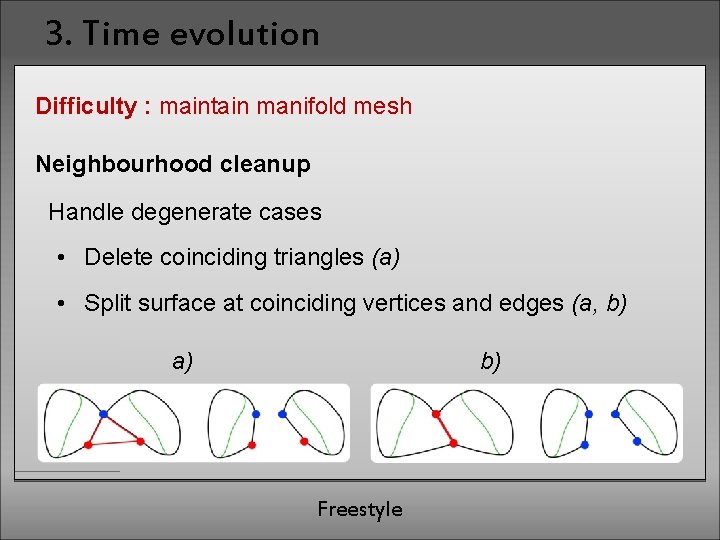
3. Time evolution Difficulty : maintain manifold mesh Neighbourhood cleanup Handle degenerate cases • Delete coinciding triangles (a) • Split surface at coinciding vertices and edges (a, b) a) b) Freestyle

4. Sculpting tools Displacement fields • Space deformations volume preserving • Model dependent normals, geodesic distance… Deformation applied discretely Large displacements • divided • max(norm) < μ Freestyle

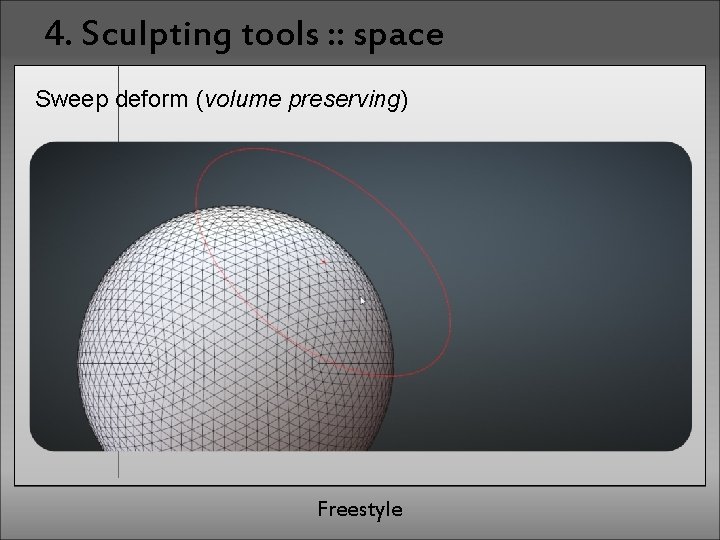
4. Sculpting tools : : space Sweep deform (volume preserving) Freestyle

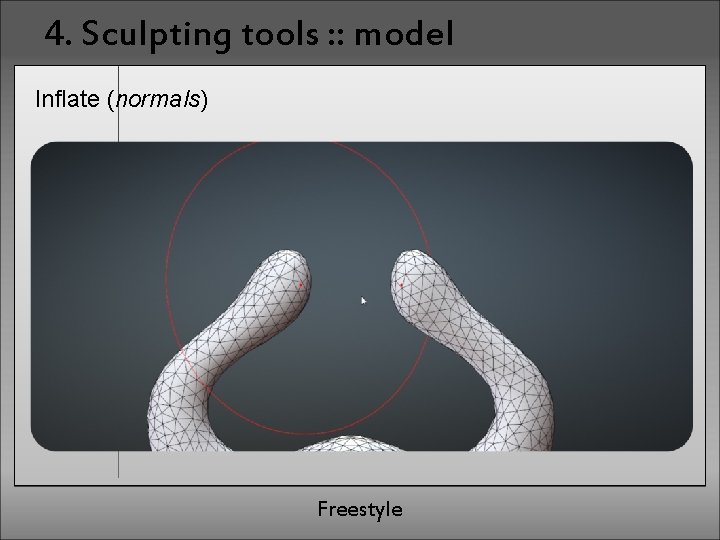
4. Sculpting tools : : model Inflate (normals) Freestyle

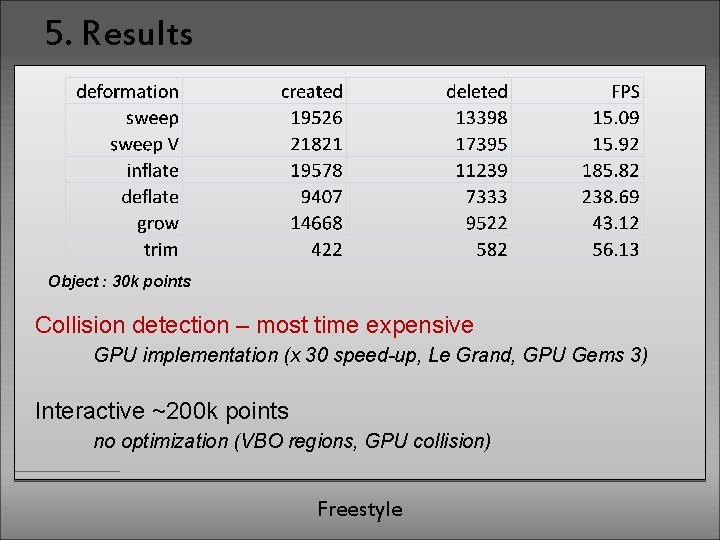
5. Results Object : 30 k points Collision detection – most time expensive GPU implementation (x 30 speed-up, Le Grand, GPU Gems 3) Interactive ~200 k points no optimization (VBO regions, GPU collision) Freestyle

6. Conclusions Handle arbitrary changes in topology simple quasi-uniform framework Intuitive model based on two physical properties of materials surface detail and bulk thickness Closer to real-life sculpting auto-refinement changes in topology Freestyle

6. Future work • Sharp features • Sculpting curves • Fast approximate Boolean operations • Surface painting • Adaptive sampling (local quasi-uniform meshes) • Further validation by professional and amateur users Freestyle

7. Demo Freestyle

Thank you ! Freestyle