FREE FALL GALILEOS DISCOVERY Which falls with more

FREE FALL

GALILEO’S DISCOVERY • Which falls with more acceleration, your physics text book or a piece of paper? • The text book will faster. • What happens if the piece of paper sits on top of the text book? • Both will fall equally the same. Why? • What happens if both objects are in a vacuum? • Both will fall equally the same. Why?

GALILEO’S DISCOVERY • Galileo noticed that objects will fall at the same rate (as long as air resistance does not affect said object) • Free Fall – is the motion of an object when gravity is the only significant force acting on it. • Free Fall Acceleration – is the acceleration of an object due only to the effect of gravity, regardless of its mass. • Free Fall Acceleration on earth is 9. 8 m/s 2 down or 9. 8 m/s 2.

ACCELERATION DUE TO GRAVITY Acceleration Due to Gravity Comparison Body Mass [kg] Radius [m] Acceleration Due to Gravity, "g" [m/s²] Sun 1. 99 x 1030 6. 96 x 108 274. 13 27. 95 Mercury 3. 18 x 1023 2. 43 x 106 3. 59 0. 37 Venus 4. 88 x 1024 6. 06 x 106 8. 87 0. 90 Earth 5. 98 x 1024 6. 38 x 106 9. 81 1. 00 Moon 7. 36 x 1022 1. 74 x 106 1. 62 0. 17 Mars 6. 42 x 1023 3. 37 x 106 3. 77 0. 38 Jupiter 1. 90 x 1027 6. 99 x 107 25. 95 2. 65 Saturn 5. 68 x 1026 5. 85 x 107 11. 08 1. 13 Uranus 8. 68 x 1025 2. 33 x 107 10. 67 1. 09 Neptune 1. 03 x 1026 2. 21 x 107 14. 07 1. 43 Pluto 1. 40 x 1022 1. 50 x 106 0. 42 0. 04 g / g-Earth

FREE FALL ACCELERATION • Since acceleration due to gravity is a constant 9. 8 m/s 2 downwards, what does this mean for velocity and distance? • Imagine I throw a ball upwards with a velocity of 20 m/s, what happens to the ball? • If I throw the ball up (positive direction) why does the ball eventually stop at the top and then proceed to drop? • Acceleration is acting on the ball.

FREE FALL ACCELERATION • As the ball is moving up (positive), acceleration due to gravity (9. 8 m/s 2) is acting against it (negative). • Therefore, as the ball moves up, every second the velocity slows down by 9. 8 m/s. • OHHHHH, so how long does it take to reach the top?

• How long does it take to reach the top? • vf =vi +at • vf =0, vi = 20. 0 m/s, a=-9. 80 m/s 2, t=? • 0 =20. 0 m/s +(-9. 80 m/s 2)(t) • t = -20. 0 m/s -9. 80 m/s 2 • t = 2. 04 seconds.

FREE FALL ACCELERATION • How high does that ball go? • d = vi t + ½ at 2 • vi =20. 0 m/s, a=-9. 80 m/s 2, t=2. 00 s, d = ? • d = (20. 0 m/s)(2. 04) + ½ (-9. 80 m/s 2)(2. 04 s)2 • d = 40. 8 + (-20. 39) • d = 20. 41 m • This is only half of the motion of the ball, the ball then comes back down to my hand. • Thus the total distance travelled is 40. 8 m, the displacement is 0 m, and the total time travelled is 4. 08 s.

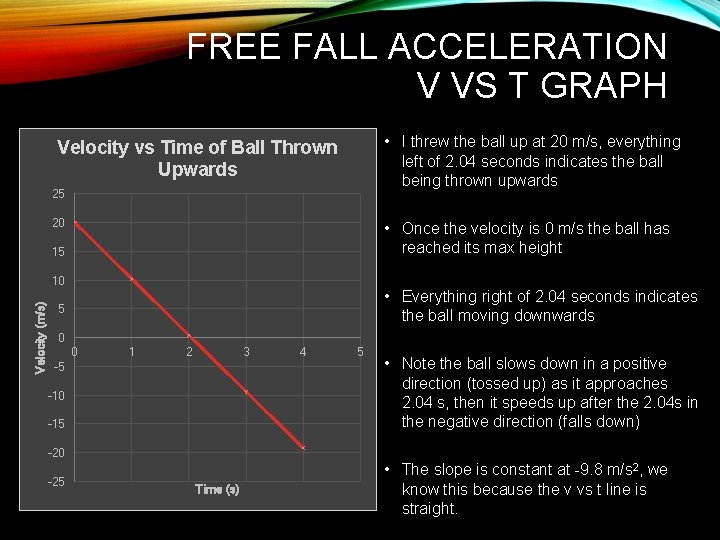
FREE FALL ACCELERATION V VS T GRAPH • I threw the ball up at 20 m/s, everything left of 2. 04 seconds indicates the ball being thrown upwards Velocity vs Time of Ball Thrown Upwards 25 20 • Once the velocity is 0 m/s the ball has reached its max height 15 Velocity (m/s) 10 • Everything right of 2. 04 seconds indicates the ball moving downwards 5 0 0 1 2 3 -5 -10 -15 4 5 • Note the ball slows down in a positive direction (tossed up) as it approaches 2. 04 s, then it speeds up after the 2. 04 s in the negative direction (falls down) -20 -25 Time (s) • The slope is constant at -9. 8 m/s 2, we know this because the v vs t line is straight.

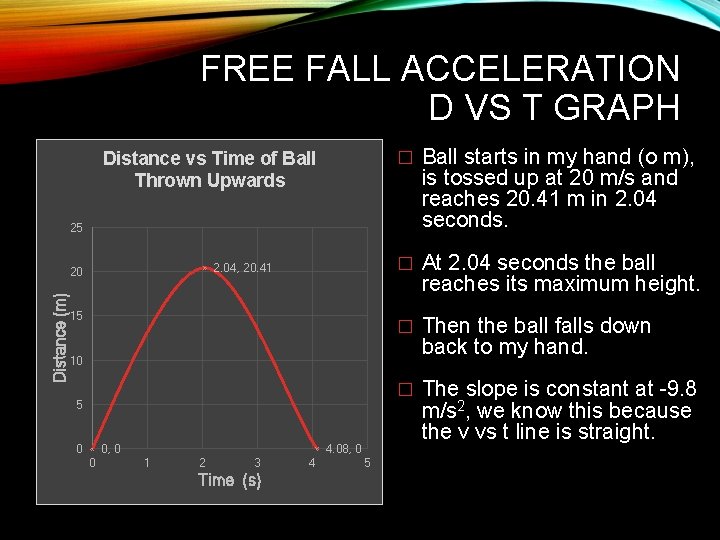
FREE FALL ACCELERATION D VS T GRAPH Distance vs Time of Ball Thrown Upwards � Ball starts in my hand (o m), is tossed up at 20 m/s and reaches 20. 41 m in 2. 04 seconds. � At 2. 04 seconds the ball reaches its maximum height. � Then the ball falls down back to my hand. � The slope is constant at -9. 8 m/s 2, we know this because the v vs t line is straight. 25 2. 04, 20. 41 Distance (m) 20 15 10 5 0 0, 0 0 4. 08, 0 1 2 3 Time (s) 4 5

FREE FALL ACCELERATION • Question, once the ball reaches 0 m/s does it fall down? • Acceleration due to gravity pulls it down at 9. 8 m/s 2 • What would happen if, when the ball reaches 0 m/s and the acceleration was 0 m/s 2? • The ball would not move, it would be in suspension and hovering.

EX. A student drops their homework down a wishing well. After 2. 4 s it hits the water at the bottom. How deep is the well? d = vi t + ½ at 2 d = (0)(2. 4 s) + ½ (-9. 8 m/s 2)(2. 4 s)2 d = 0 – 28. 224 m d = -28. 2 m

EXAMPLE A football is kicked straight up in the air at 15. 0 m/s. a) How high does it go? b) What is its total hang time? Solution a) vf = vi +at 0 = 15. 0 m/s + (-9. 80 m/s 2)(t) t = -15. 0 m/s -9. 80 m/s 2 t = 1. 5306…. S Or vf 2 = vi 2 – 2 ad b) t total = (1. 5306 s)(2) = 3. 06122 seconds = 3. 06 seconds d = vi t + ½ at 2 d = (15. 0 m/s)(1. 5306… s) +½(-9. 80 m/s 2)(1. 5306…s)2 d = 22. 959… m – 11. 47959 m d = 11. 4794 m d = 11. 5 m

HOMEWORK • Pg 78, Q’s 41 – 45 • Handout on uniform acceleration