Free electron theory Introduction 1 The electron theory

Free electron theory

Introduction 1. The electron theory of metals aims to explain the structure and properties of solids through their electronic structure. The electron theory is applicable to all solids i. e. , both metals and non metals. It explains the electrical, thermal and magnetic properties of solids etc. 2. The theory assumes the motion of electrons inside the atom as motion inside a constant potential and hence treated them as free. 3. Drude and Lorentz in 1900 used this free electron model to explain the electrical and thermal properties of metals. He assumed that the free electrons in a metal behave like molecules of a perfect gas obeying Maxwell-Boltzmann statistics. 4. The theory provides correct explanation of electrical resistance with temperature but fails to explain many other experimental facts like variation of electrical resistivity, heat capacity and paramagnetic susceptibility of conduction electrons etc. .

Characteristics of metals 1. 2. 3. Obeys ohm’s law : V = R × I. Resistance R is related to the length L and the cross-section area A by a simple formula R = L A × ρ, where the electric resistivity ρ is material dependent (as well as its temperature and pressure), but not on the geometry of the conducting body. The inverse of the resistivity σ = 1/ρ is called the electric conductivity. V = (L × ρ x I)/A 1/ ρ (V/L) = (I/A) σ E = J; where J is current density. Metals have high electrical and thermal conductivity. Metals obey the Wiedemann–Franz law which states that the ratio of the electronic contribution of thermal conductivity (K) to the electrical conductivity (σ) of a metal is proportional to the temperature i. e. K/σ = LT; where L is a constant called Lorentz’s number and T is temperature.

Drude-Lorentz Theory of Electrical Conduction The basic assumptions of Lorentz-Drude theory are: 1. There a large number of free electrons in a metal. These electrons are free to move about the whole volume of the metal like the molecules of a perfect gas in a container. 2. The free electrons make collisions from time to time with fixed positive ions in the lattice and also among themselves. We may neglect the collisions between electrons in comparison with the collisions between electrons and ions cores. 3. In the absence of electric field, the random motion of free electrons is equally probable in all directions so that current density vector is zero. 4. When an external electric field is applied, the electrons drift slowly with some average velocity, known as average drift velocity, in the direction opposite to that of electric field. The drift velocity is much smaller in magnitude than average random velocity of free electrons. The average distance transverse by a free electron between two successive collisions with the positive ions is called mean free path and is denoted by λ. 5. If an electron of mass m and charge e is placed in an electric field E, it experiences an acceleration a given by: a = e. E/m. Let τ be the average time – interval between two successive collisions of an electron with positive ions. This drift velocity is reduced to zero at the next collision and again builds up to the value e. Eτ/m before suffering another collision and so on therefore the average drift velocity through the conductor = V d = e. Eτ/m Let n be the number of conduction electrons per unit volume. Current density = J = nevd = ne 2 Eτ /m But J = σ = J/E = ne 2τ /m; which is the expression for the electrical conductivity of a metal.

Limitations of Free Electron Theory: (a) It cannot explain why only some crystals are metallic in nature. (b) It cannot explain why the observed specific heat of metals is only 1% of the calculated value (i. e. , 3/2 N KB; N are number of free electrons per gram atom). (c) It cannot explain the temperature variation of the electrical conductivity. (d) It cannot explain the paramagnetic behavior of metals. (e) It also could not explain the occurrence of long mean free paths at low temperatures.

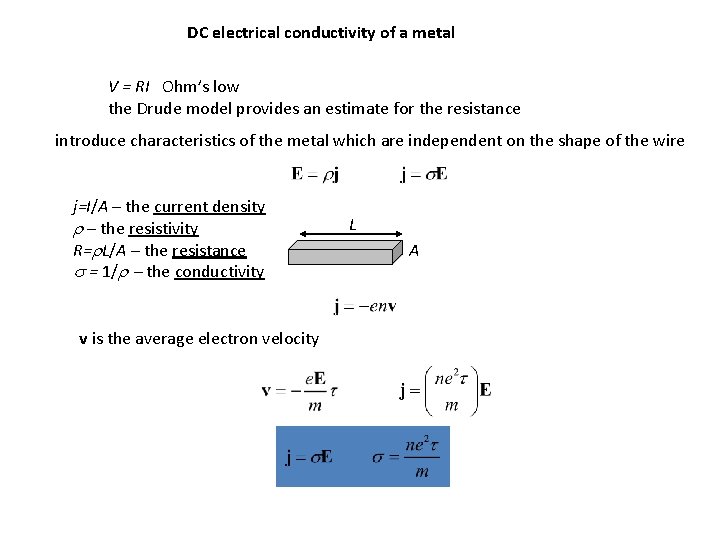
DC electrical conductivity of a metal V = RI Ohm’s low the Drude model provides an estimate for the resistance introduce characteristics of the metal which are independent on the shape of the wire j=I/A – the current density r – the resistivity R=r. L/A – the resistance s = 1/r - the conductivity v is the average electron velocity L A

at room temperatures resistivities of metals are typically of the order of micro-ohm centimeters (mohm-cm) and t is typically 10 -14 – 10 -15 s mean free path l=v 0 t v 0 – the average electron speed l measures the average distance an electron travels between collisions estimate for v 0 at Drude’s time → v 0 ~107 cm/s → l ~ 1 – 10 Å consistent with Drude’s view that collisions are due to electron bumping into ions at low temperatures very long mean free path can be achieved l > 1 cm ~ 108 interatomic spacings! the electrons do not simply bump off the ions! the Drude model can be applied where a precise understanding of the scattering mechanism is not required

Widemann Franz Law It states that ratio of thermal conductivity (K) to that of electrical conductivity (σ) of a metal is a constant. Electrical conductivity σ = = ne 2τ/m Thermal conductivity K = 1/3 v 2τCv Now Cv = 3/2 Nk and 1/2 mv 2 = 3/2 k. T, where N = Avagadro’s no. And k is Boltzmann constant. K/ σT = constant = 2. 4 x 10 -8 WΏK-2

Failures of Drude’s model The free electron model explains many important properties of conductors but is weak in at least two areas. 1. It assumes a constant potential energy within the solid. (i. e. the electron experience no forces. ) 2. The free electron model assumes an impenetrable barrier at the surface. This assumption is not valid, because under certain conditions, electrons can escape the surface —such as in the photoelectric effect. In addition to these assumptions, the free electron model does not explain the dramatic differences in electronic properties of conductors, semiconductors, and insulators. Therefore, a more complete model is needed.

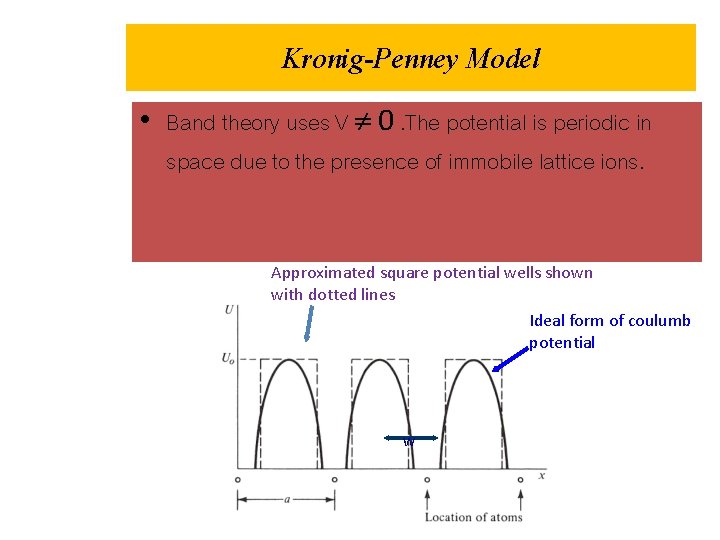
Kronig-Penney Model • Band theory uses V 0. The potential is periodic in space due to the presence of immobile lattice ions. Approximated square potential wells shown with dotted lines Ideal form of coulumb potential w

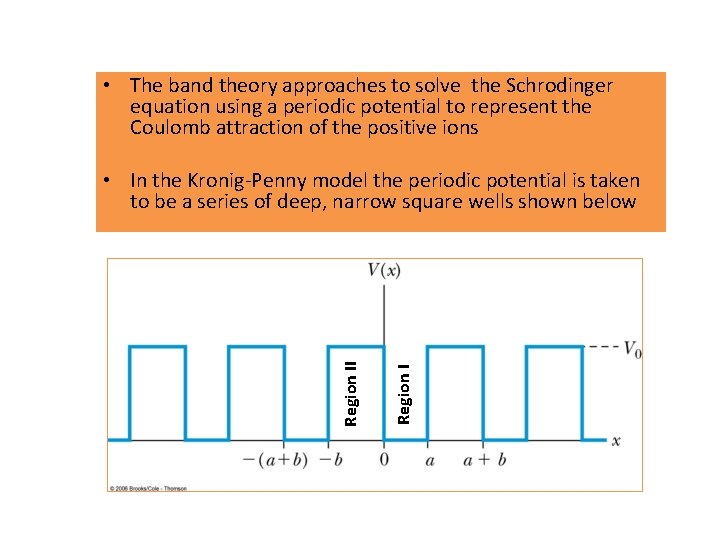
• The band theory approaches to solve the Schrodinger equation using a periodic potential to represent the Coulomb attraction of the positive ions Region II • In the Kronig-Penny model the periodic potential is taken to be a series of deep, narrow square wells shown below

Band Theory • We have to solve the Schrodinger equation for both the regions Then apply the boundary conditions viz: Wave function and its first derivative are continuous at the boundaries • It turns out that there are other conditions to consider since lattice is periodic hence the wave function should also be periodic with the periodicity that of the lattice. 12