Frao Parte ou pedao de um inteiro Exemplos

Fração Ø Parte ou pedaço de um inteiro.

Exemplos do Uso da Fração no Dia-a-Dia Ø Ao dividir uma pizza;

Exemplos do Uso da Fração no Dia-a-Dia Ø Ao dividir um bolo;

Exemplos do Uso da Fração no Dia-a-Dia Ø Na contagem das raças de um país; 100 90 80 Millions 70 60 50 40 30 20 10 0 Negros Brancos Índios

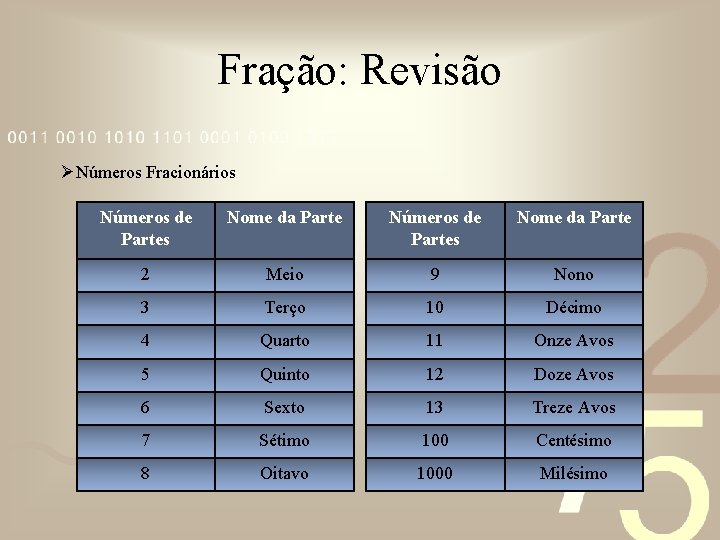
Fração: Revisão ØNúmeros Fracionários Números de Partes Nome da Parte 2 Meio 9 Nono 3 Terço 10 Décimo 4 Quarto 11 Onze Avos 5 Quinto 12 Doze Avos 6 Sexto 13 Treze Avos 7 Sétimo 100 Centésimo 8 Oitavo 1000 Milésimo

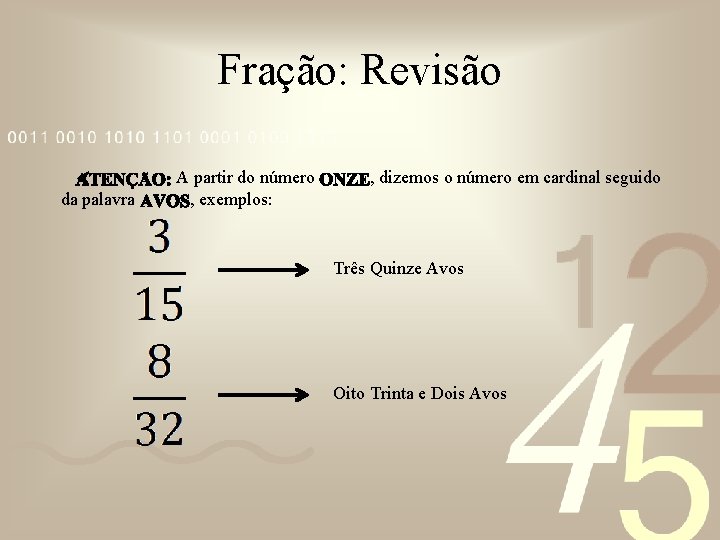
Fração: Revisão da palavra A partir do número , exemplos: , dizemos o número em cardinal seguido Três Quinze Avos Oito Trinta e Dois Avos

Fração: Revisão ØO número que está embaixo – números de divisões – é chamado de. ØO número que está em cima – número de partes escolhidas – é chamado de

Fração: Revisão O numerador é menor que o denominador; O numerador é maior que o denominador; O numerador é múltiplo do denominador;

Fração: Revisão Quando 2 ou mais frações tem a mesma quantidade “pegas” de um mesmo todos. ØSe comemos de pizza é o mesmo que comermos ou de pizza.

Fração: Número Misto ØComo representar DUAS PIZZAS faltando pedaços em uma FRAÇÃO? ØRESPOSTA: Utilizando o NÚMERO MISTO – Um número formado por um número inteiro junto de uma fração.

Fração: Número Misto ØUm bolo inteiro mais um pedaço do bolo do mesmo tamanho, podemos dizer que temos: de bolo de fubá

Fração: Número Misto Parte Inteira Parte Fracionária ou Fração

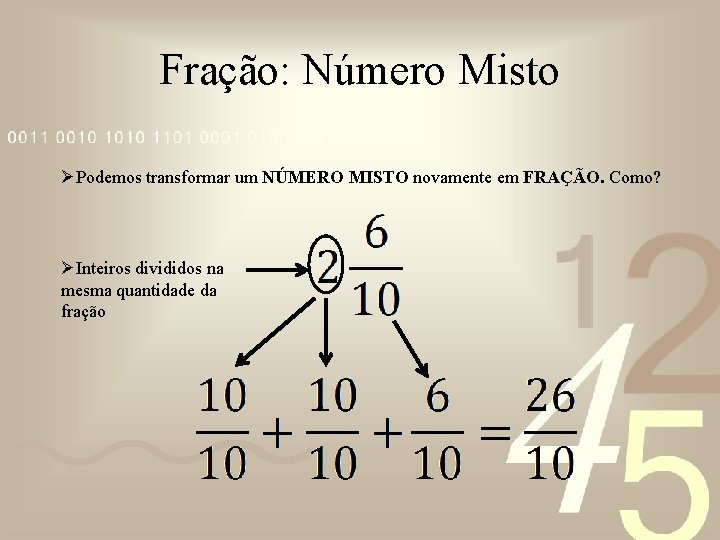
Fração: Número Misto ØPodemos transformar um NÚMERO MISTO novamente em FRAÇÃO. Como? ØInteiros divididos na mesma quantidade da fração

Fração: Número Misto ØPodemos transformar um NÚMERO MISTO novamente em FRAÇÃO usando um outro modo: ØMultiplicar a parte inteira pelo DENOMINADOR + X ØO resultado da multiplicação soma-se o NUMERADOR. ØEntão temos: ØLEMBRE-SE: O DENOMINADOR continua o mesmo.

Fração: Simplificação da Fração ØO que é mais fácil? Repartir uma multidão em OITO GRUPOS e escolher DOIS?

Fração: Simplificação da Fração ØOu repartir uma multidão em QUATRO GRUPOS e escolher UM?

Fração: Simplificação da Fração ØSe o divisor é menor possível, a divisão fica mais fácil!!! Então é melhor simplificar a fração. ØQuando temos a fração quando numeradores e denominadores GRANDES, o melhor a fazer são simplificá-los. COMO? : 2 : 4 OU : 2 : 4 ØBasta escolher um número que DIVIDE O NUMERADOR E O DENOMINADOR AO MESMO TEMPO. ØQuanto MENOR a fração MELHOR a simplificação.

Fração: Simplificação da Fração ØSe não temos como simplificar mais a fração ou não conseguimos simplificá-la de início. : 4 : 2 OU : 4 : 2 ØTemos uma FRAÇÃO IRREDUTÍVEL, que não se pode mais SIMPLIFICAR.

Fração: Operações Aritméticas Adição ØCarlos comprou uma barra de chocolate e comeu dois pedaços. Maria comprou uma barra de chocolate igual a de Carlos, mas ela só comeu um pedaço. Eles decidiram juntar a duas barras. Quantos pedaços eles tem? E quantas frações eles tem? Carlos Maria

Fração: Operações Aritméticas Adição ØCarlos comprou uma barra de chocolate e comeu dois pedaços. Maria comprou uma barra de chocolate igual a de Carlos, mas ela só comeu um pedaço. Eles decidiram juntar a duas barras. Quantos pedaços eles tem? E quantas frações eles tem? Carlos Maria

Fração: Operações Aritméticas Adição ØCarlos tem da barra de chocolate. Carlos Maria ØMaria tem da barra de chocolate.

Fração: Operações Aritméticas Adição ØJunto eles tem: 9 PEDAÇOS OU

Fração: Operações Aritméticas Adição ØQuando os DENOMINADORES SÃO IGUAIS, BASTA SOMAR OS NUMERADORES.

Fração: Operações Aritméticas Adição ØQuando os DENOMINADORES SÃO DIFERENTES, TEMOS SEGUINTES REGRAS A SEGUIR.

Fração: Operações Aritméticas Adição ØPRIMEIRO, DEVE ENCONTRA O MÍNIMO MÚLTIPLO COMUM DOS DENOMINADORES. 5, 2 2 5, 1 5 1 , 1 10 ØO VALOR DO M. M. C. (10) SUBSTITUIRÁ OS DENOMINADORES ANTIGOS (5 E 2).

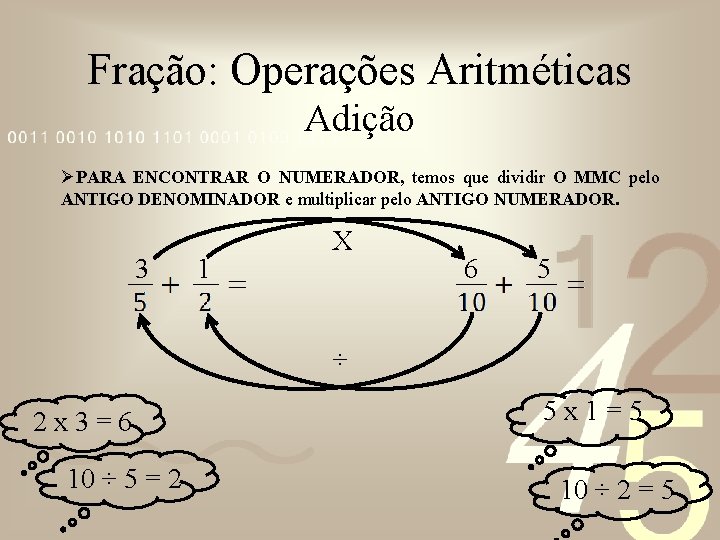
Fração: Operações Aritméticas Adição ØPARA ENCONTRAR O NUMERADOR, temos que dividir O MMC pelo ANTIGO DENOMINADOR e multiplicar pelo ANTIGO NUMERADOR. 3 1 X 6 5 ÷ 2 x 3=6 10 ÷ 5 = 2 5 x 1=5 10 ÷ 2 = 5

Fração: Operações Aritméticas Adição ØPOR FIM, SOMA-SE OS “NOVOS” NUMERADORES, repetindo o DENOMINADOR.

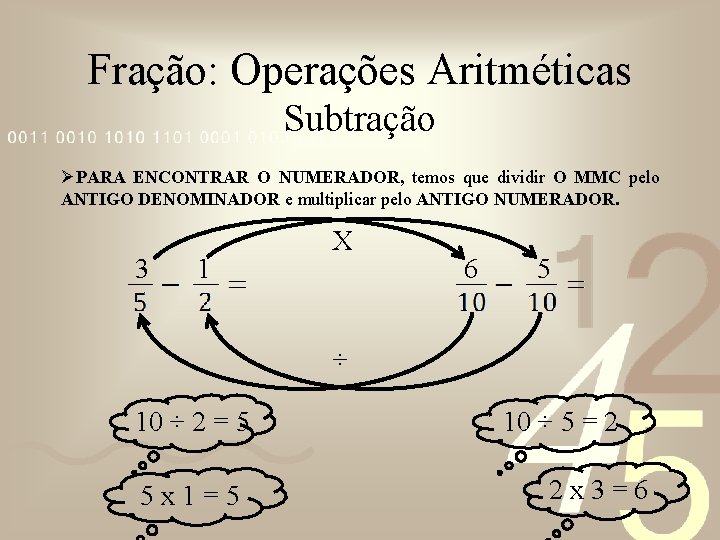
Fração: Operações Aritméticas Subtração ØQuando os DENOMINADORES SÃO DIFERENTES, TEMOS QUE SEGUIR AS MESMAS REGRAS DA ADIÇÃO.

Fração: Operações Aritméticas Subtração ØPRIMEIRO, DEVE ENCONTRA O MÍNIMO MÚLTIPLO COMUM DOS DENOMINADORES. 5, 2 2 5, 1 5 1 , 1 10 ØO VALOR DO M. M. C. (10) SUBSTITUIRÁ OS DENOMINADORES ANTIGOS (5 E 2).

Fração: Operações Aritméticas Subtração ØPARA ENCONTRAR O NUMERADOR, temos que dividir O MMC pelo ANTIGO DENOMINADOR e multiplicar pelo ANTIGO NUMERADOR. 3 1 X 6 5 ÷ 10 ÷ 2 = 5 5 x 1=5 10 ÷ 5 = 2 2 x 3=6

Fração: Operações Aritméticas Subtração ØPOR FIM, SOMA-SE OS “NOVOS” NUMERADORES, repetindo o DENOMINADOR.

Fração: Operações Aritméticas Multiplicação ØCoralina comprou um terreno onde DOIS TERÇOS do terreno foi construído a casa. Em UM QUINTO do restante foi construído um jardim e em QUATRO QUINTOS uma piscina. Em relação ao terreno todo quanto foi ocupado pelo jardim? Quanto foi ocupado pela piscina?

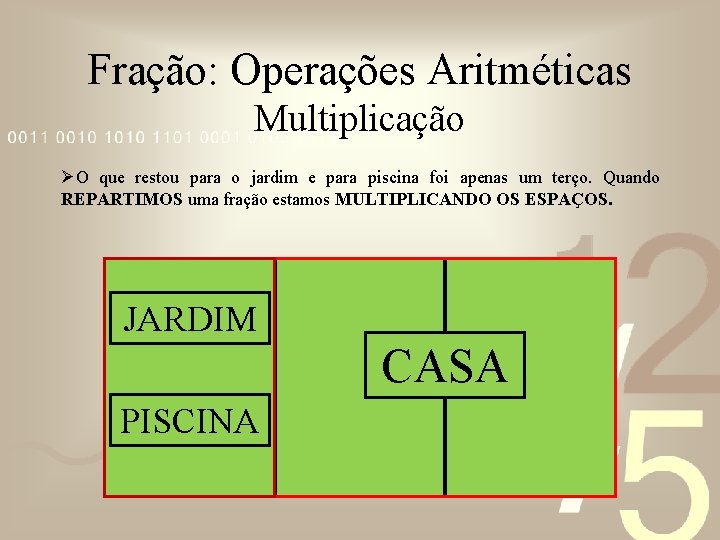
Fração: Operações Aritméticas Multiplicação ØO que restou para o jardim e para piscina foi apenas um terço. Quando REPARTIMOS uma fração estamos MULTIPLICANDO OS ESPAÇOS.

Fração: Operações Aritméticas Multiplicação ØO que restou para o jardim e para piscina foi apenas um terço. Quando REPARTIMOS uma fração estamos MULTIPLICANDO OS ESPAÇOS. JARDIM CASA PISCINA

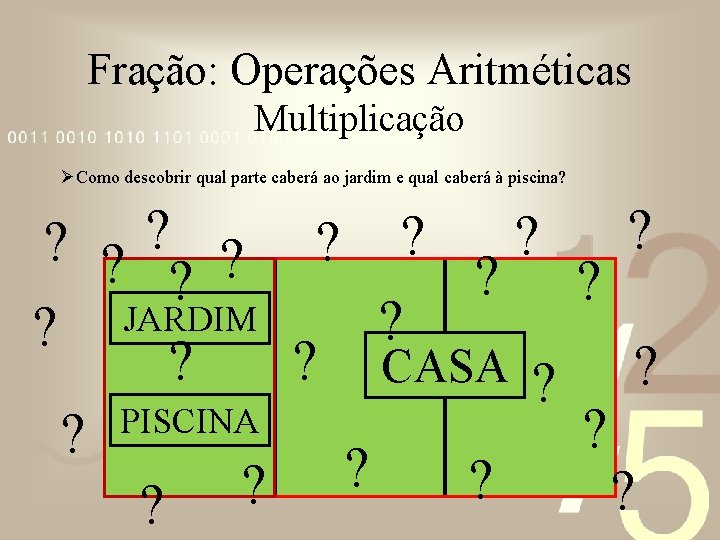
Fração: Operações Aritméticas Multiplicação ØComo descobrir qual parte caberá ao jardim e qual caberá à piscina? ? ? ? JARDIM ? ? CASA ? ? PISCINA ? ? ? ?

Fração: Operações Aritméticas Multiplicação ØBasta multiplicar o que restou para o jardim pelo o pedaço que o jardim vai ocupar. NUMERADOR VEZES NUMERADOR e DENOMINADOR VEZES DENOMINADOR. ØBasta multiplicar o que restou para a piscina pelo o pedaço que a piscina vai ocupar. NUMERADOR VEZES NUMERADOR e DENOMINADOR VEZES DENOMINADOR.

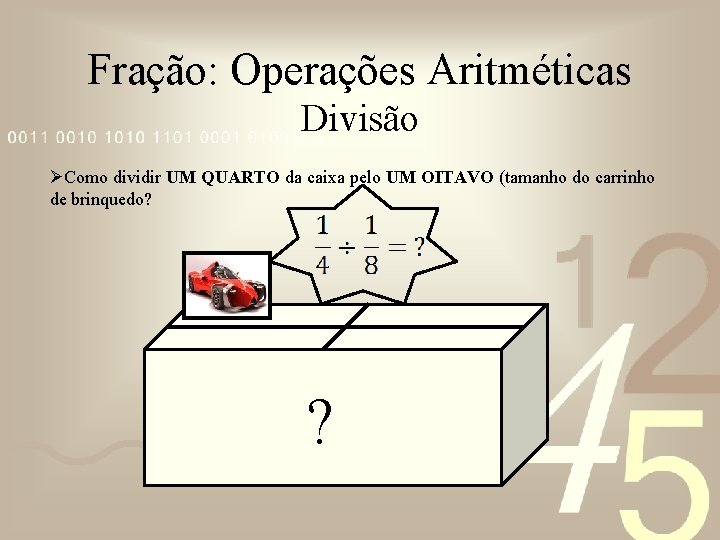
Fração: Operações Aritméticas Divisão ØJoaquim comprou uma caixa DIVIDIDA EM 4 PARTES para guardar carrinhos de brinquedo. Cada carrinho tem UM OITAVO DO TAMANHO DA CAIXA, então quantos carrinhos de brinquedo cabem em cada parte da caixa?

Fração: Operações Aritméticas Divisão ØComo dividir UM QUARTO da caixa pelo UM OITAVO (tamanho do carrinho de brinquedo? ?

Fração: Operações Aritméticas Divisão ØSOLUÇÃO: Temos uma regra: 1) Repete a primeira fração; 2) Inverta a segunda fração (denominador vai para o lugar do numerador e o numerador vai para o lugar do denominador); 3) E por fim, multiplique as frações. X =

Fração: Operações Aritméticas Divisão ØComo saber quanto a FRAÇÃO RESULTANTE (O RESULTADO) representa em questão de espaço? ØSOLUÇÃO: Basta dividir o NUMERADOR PELO DENOMINADOR! 2 ØEntão, cabem 2 carrinhos de brinquedo em cada parte da caixa. ØATENÇÃO: Se não der para dividir apenas simplifique a fração resultante. ?

Fração: Operações Aritméticas Divisão ØEm cada parte cabem 2 carrinhos de brinquedos.