Frank Cowell Microeconomics October The Firm Basics MICROECONOMICS

Frank Cowell: Microeconomics October The Firm: Basics MICROECONOMICS Principles and Analysis Frank Cowell

Overview. . . The Firm: Basics Frank Cowell: Microeconomics The setting The environment for the basic model of the firm. Input requirement sets Isoquants Returns to scale Marginal products

The basics of production. . . Frank Cowell: Microeconomics n Some of the elements needed for an analysis of the firm u u u n n n Technical efficiency Returns to scale Convexity Substitutability Marginal products This is in the context of a single-output firm. . . and assuming a competitive environment. First we need the building blocks of a model. . .

Notation Frank Cowell: Microeconomics n Quantities zi z = (z 1, z 2 , . . . , zm ) q • amount of input i • input vector • amount of output For next presentation n Prices wi w = (w 1, w 2 , . . . , wm ) p • price of input i • Input-price vector • price of output

Feasible production Frank Cowell: Microeconomics The basic relationship between The production output and function inputs: n • single-output, multiple-input production relation q £ (z 1, z 2, . . , zm ) This can be written more compactly as: Vector of inputs n q £ (z) n gives the maximum amount of output that can be produced from a given list of inputs • Note that we use “£” and not “=” in the relation. Why? • Consider the meaning of distinguish two important cases. . .

Technical efficiency Frank Cowell: Microeconomics n Case 1: q = (z) n Case 2: q < (z) • The case where production is technically efficient • The case where production is (technically) inefficient Intuition: if the combination (z, q) is inefficient you can throw away some inputs and still produce the same output
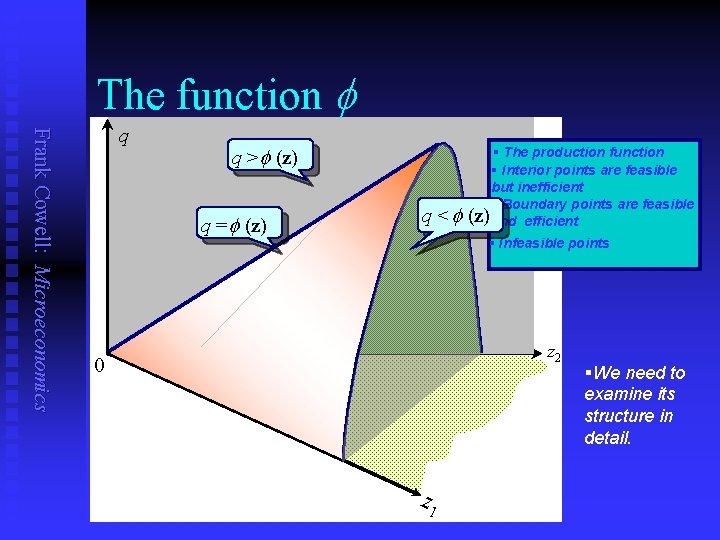
The function Frank Cowell: Microeconomics q q > (z) q = (z) q < § The production function § Interior points are feasible but inefficient § Boundary points are feasible (z) and efficient § Infeasible points z 2 0 z 1 §We need to examine its structure in detail.

Overview. . . The Firm: Basics Frank Cowell: Microeconomics The setting The structure of the production function. Input requirement sets Isoquants Returns to scale Marginal products

The input requirement set Frank Cowell: Microeconomics n Pick a particular output level q n Find a feasible input vector z n Repeat to find all such vectors n Yields the input-requirement set Z(q) : = {z: (z) ³ q} The shape of Z depends on the assumptions made about production. . . n We will look at four cases. n remember, we must have q £ (z) n The set of input vectors that meet the technical feasibility condition for output q. . . n First, the “standard” case.
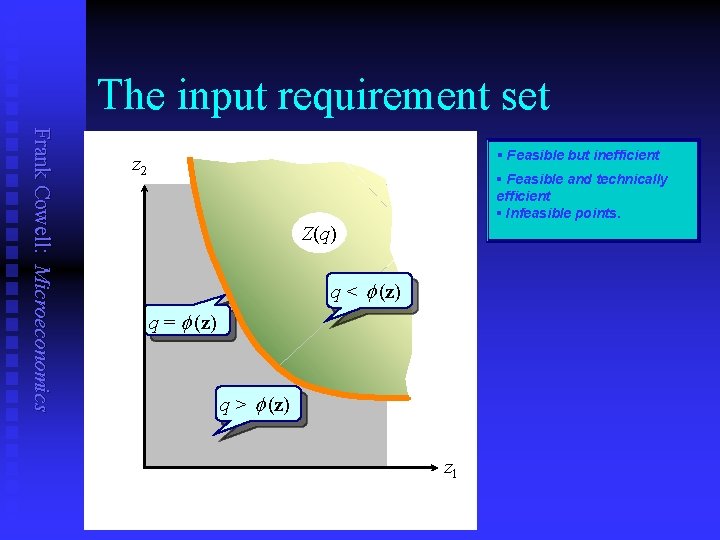
The input requirement set Frank Cowell: Microeconomics § Feasible but inefficient z 2 § Feasible and technically efficient § Infeasible points. Z(q) q < (z) q = (z) q > (z) z 1

Case 1: Z smooth, strictly convex Frank Cowell: Microeconomics § Pick two boundary points § Draw the line between them z 2 § Intermediate points lie in the interior of Z. Z(q) l q = (z') z¢ §Note important role of convexity. q< (z) l §A combination of two techniques may produce more output. z² q = (z") z 1 §What if we changed some of the assumptions?

Case 2: Z Convex (but not strictly) Frank Cowell: Microeconomics § Pick two boundary points § Draw the line between them z 2 § Intermediate points lie in Z (perhaps on the boundary). Z(q) l z¢ l z² z 1 § A combination of feasible techniques is also feasible

Case 3: Z smooth but not convex Frank Cowell: Microeconomics § Join two points across the “dent” § Take an intermediate point z 2 § Highlight zone where this can occur. Z(q) This point is infeasible § in this region there is an indivisibility l z 1
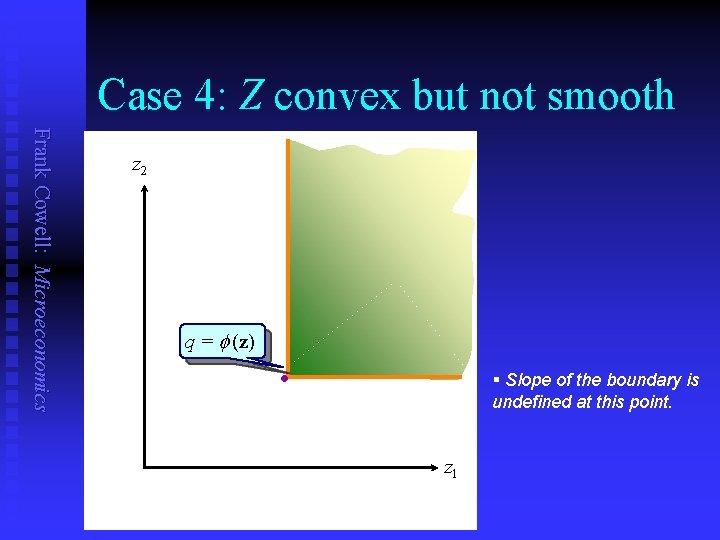
Case 4: Z convex but not smooth Frank Cowell: Microeconomics z 2 q = (z) § Slope of the boundary is undefined at this point. l z 1

Summary: 4 possibilities for Z Frank Cowell: Microeconomics z 2 z 1 Standard case, but strong assumptions about divisibility and smoothness z 2 Problems: the "dent" represents an indivisibility z 2 z 1 Almost conventional: mixtures may be just as good as single techniques Only one efficient point and not smooth. But not perverse. z 1

Overview. . . The Firm: Basics Frank Cowell: Microeconomics The setting Contours of the production function. Input requirement sets Isoquants Returns to scale Marginal products

Isoquants Frank Cowell: Microeconomics n Pick a particular output level q Find the input requirement set Z(q) n Think of the isoquant as an integral part of the set Z(q). . . n The isoquant is the boundary of Z: n { If z : the (z) = q } is differentiable at z function n the marginal rate of technical substitution is the slope at z: j (z) —— i (z) Gives the rate at which you can trade off one input against another along the isoquant, to maintain n Where appropriate, use subscript to denote partial derivatives. So n ¶ (z) i(z) : = —— ¶zi Let’s look at its shape .
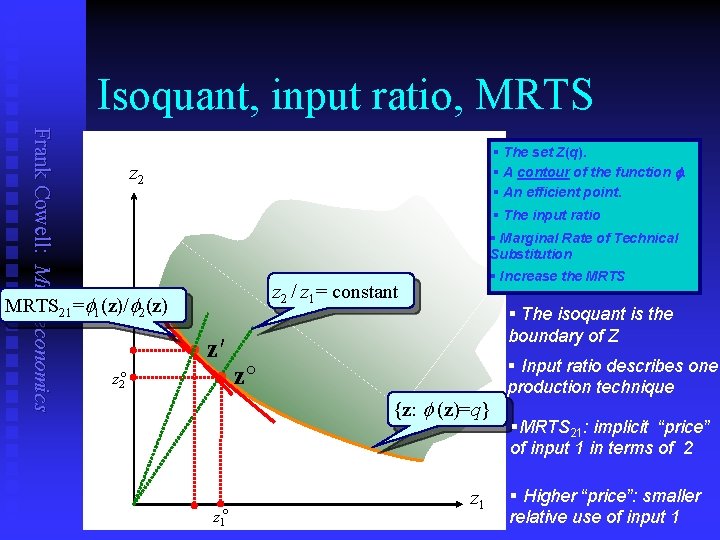
Isoquant, input ratio, MRTS Frank Cowell: Microeconomics § The set Z(q). § A contour of the function f. § An efficient point. z 2 § The input ratio § Marginal Rate of Technical Substitution z 2 / z 1= constant MRTS 21= 1(z)/ 2(z) z 2° § Increase the MRTS § The isoquant is the boundary of Z · z′ · z° {z: (z)=q} z 1° z 1 § Input ratio describes one production technique §MRTS 21: implicit “price” of input 1 in terms of 2 § Higher “price”: smaller relative use of input 1
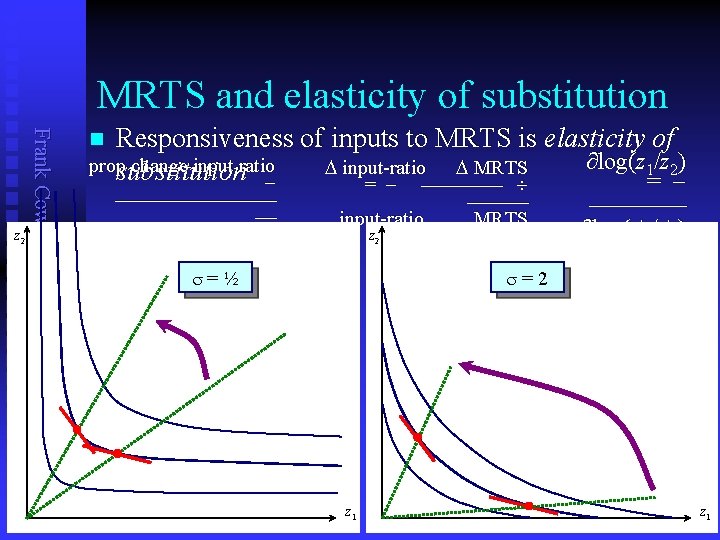
MRTS and elasticity of substitution Frank Cowell: Microeconomics z 2 Responsiveness of inputs to MRTS is elasticity of ∂log(z 1/z 2) propsubstitution change input ratio D input-ratio D MRTS = = n prop change in MRTS input-ratio z 2 s=½ MRTS ∂log( 1/ 2) s=2 z 1
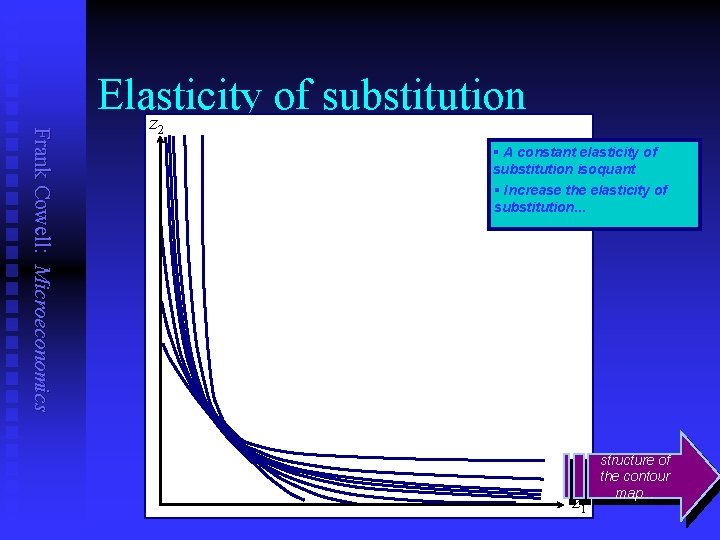
Frank Cowell: Microeconomics Elasticity of substitution z 2 § A constant elasticity of substitution isoquant § Increase the elasticity of substitution. . . z 1 structure of the contour map. . .
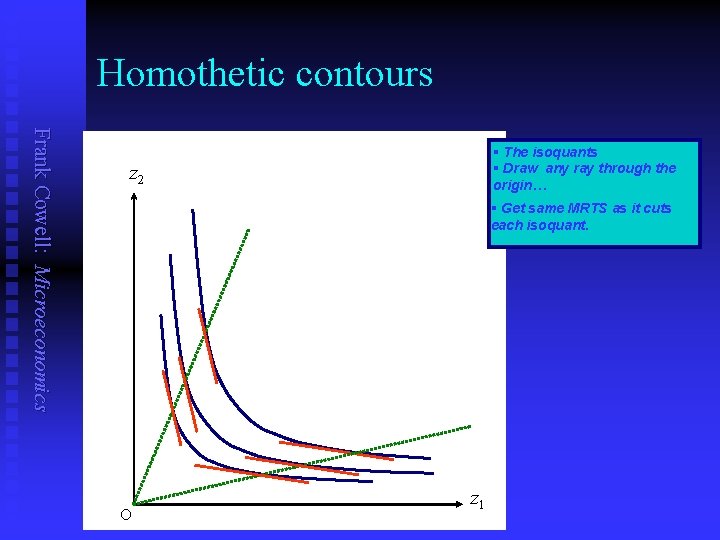
Homothetic contours Frank Cowell: Microeconomics § The isoquants § Draw any ray through the origin… z 2 § Get same MRTS as it cuts each isoquant. O z 1
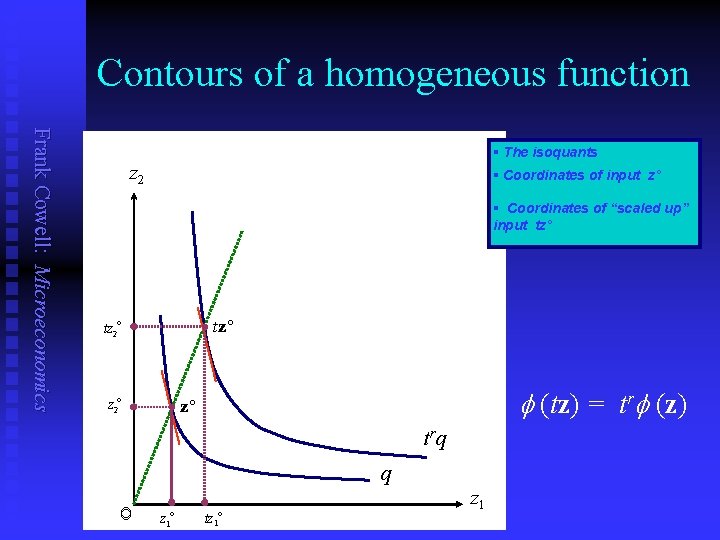
Contours of a homogeneous function Frank Cowell: Microeconomics § The isoquants z 2 § Coordinates of input z° § Coordinates of “scaled up” input tz° · tz° tz 2° (tz) = tr (z) · z° t rq q O z 1° tz 1° z 1

Overview. . . The Firm: Basics Frank Cowell: Microeconomics The setting Changing all inputs together. Input requirement sets Isoquants Returns to scale Marginal products

Let's rebuild from the isoquants Frank Cowell: Microeconomics n n The isoquants form a contour map. If we looked at the “parent” diagram, what would we see? Consider returns to scale of the production function. Examine effect of varying all inputs together: u u n Take three standard cases: u u u n Focus on the expansion path. q plotted against proportionate increases in z. Increasing Returns to Scale Decreasing Returns to Scale Constant Returns to Scale Let's do this for 2 inputs, one output…

Case 1: IRTS Frank Cowell: Microeconomics q § An increasing returns to scale function § Pick an arbitrary point on the surface § The expansion path… l z 2 0 § t>1 implies (tz) > t (z) z 1 §Double inputs and you more than double output
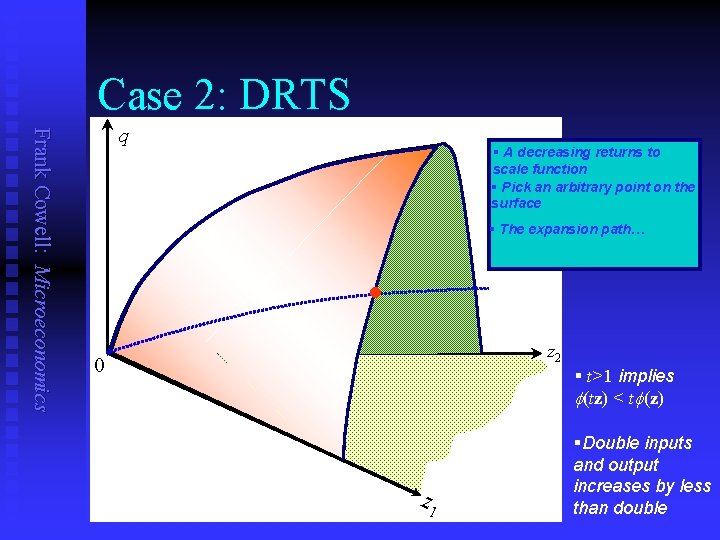
Case 2: DRTS Frank Cowell: Microeconomics q § A decreasing returns to scale function § Pick an arbitrary point on the surface § The expansion path… l z 2 0 § t>1 implies (tz) < t (z) z 1 §Double inputs and output increases by less than double
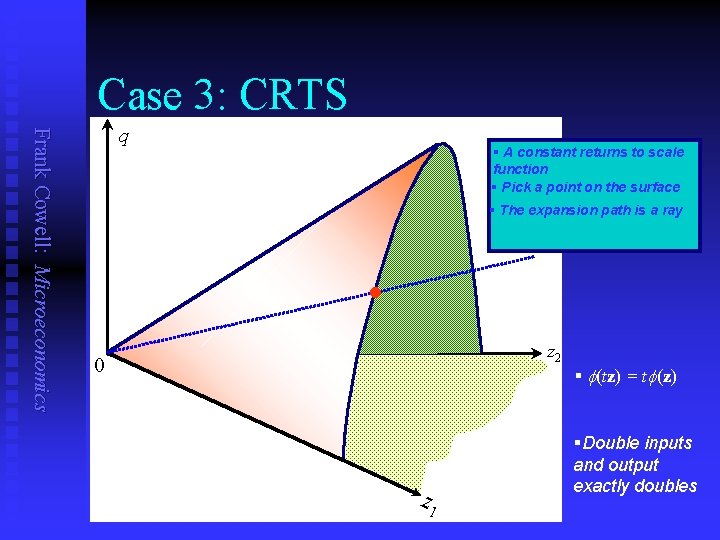
Case 3: CRTS Frank Cowell: Microeconomics q § A constant returns to scale function § Pick a point on the surface § The expansion path is a ray l z 2 0 z 1 § (tz) = t (z) §Double inputs and output exactly doubles
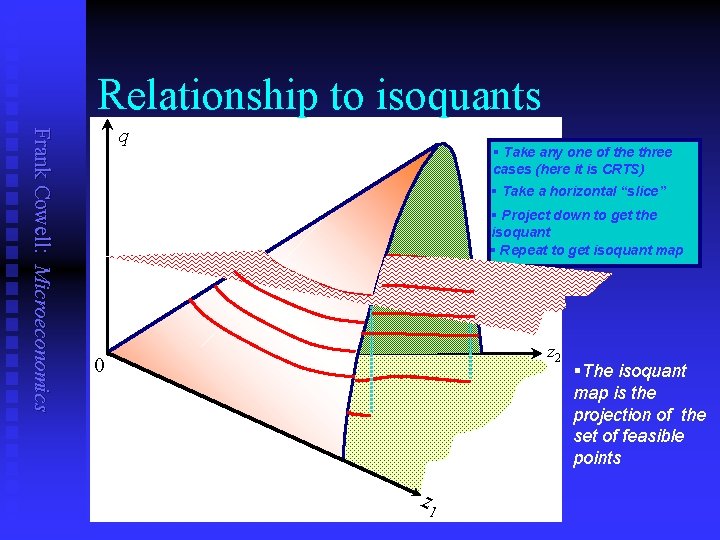
Relationship to isoquants Frank Cowell: Microeconomics q § Take any one of the three cases (here it is CRTS) § Take a horizontal “slice” § Project down to get the isoquant § Repeat to get isoquant map z 2 0 z 1 §The isoquant map is the projection of the set of feasible points

Overview. . . The Firm: Basics Frank Cowell: Microeconomics The setting Changing one input at time. Input requirement sets Isoquants Returns to scale Marginal products

Marginal products Frank Cowell: Microeconomics Pick a technically efficient input vector Remember, this means a z such that q= (z) n n n Keep all but one input constant Measure the marginal change in output w. r. t. this input n ¶ (z) MPi = i(z) = —— ¶zi. The marginal product n
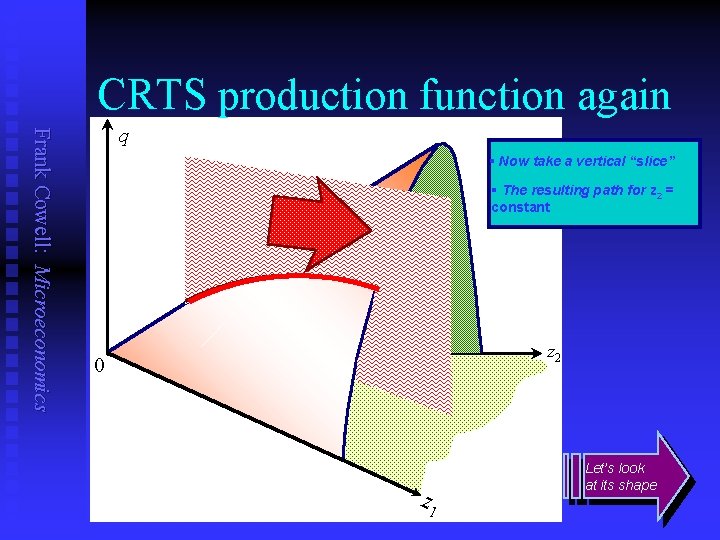
CRTS production function again Frank Cowell: Microeconomics q § Now take a vertical “slice” § The resulting path for z 2 = constant z 2 0 z 1 Let’s look at its shape
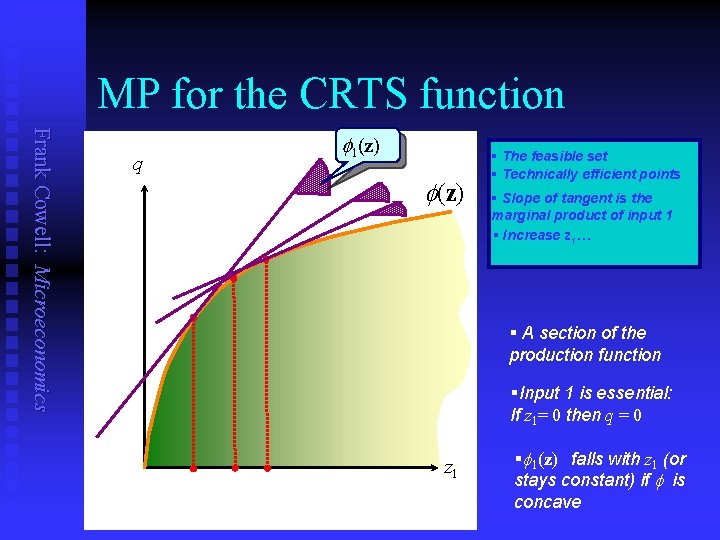
MP for the CRTS function Frank Cowell: Microeconomics q 1(z) § The feasible set § Technically efficient points § Slope of tangent is the marginal product of input 1 § Increase z 1… § A section of the production function §Input 1 is essential: If z 1= 0 then q = 0 z 1 § 1(z) falls with z 1 (or stays constant) if is concave
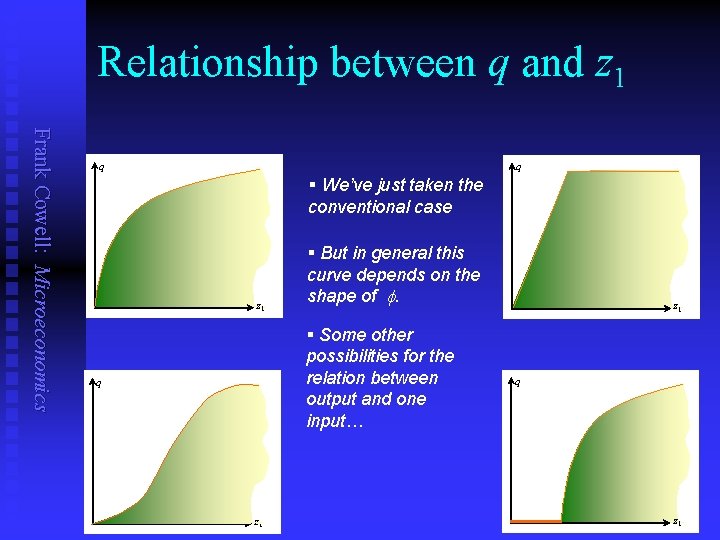
Relationship between q and z 1 Frank Cowell: Microeconomics q q § We’ve just taken the conventional case z 1 § But in general this curve depends on the shape of . § Some other possibilities for the relation between output and one input… q z 1

Key concepts Frank Cowell: Microeconomics Review Review Technical efficiency n Returns to scale n Convexity n MRTS n Marginal product n

What next? Frank Cowell: Microeconomics Introduce the market n Optimisation problem of the firm n Method of solution n Solution concepts. n
- Slides: 35





















































