Frank Cowell Microeconomics June 2006 Convexity MICROECONOMICS Principles

Frank Cowell: Microeconomics June 2006 Convexity MICROECONOMICS Principles and Analysis Frank Cowell

Convex sets Frank Cowell: Microeconomics Ideas of convexity used throughout microeconomics n Restrict attention to real space Rn ( 1, x 2, . . . , xn) n I. e. sets of vectors (x n Use the concept of convexity to define n Convex functions u Concave functions u Quasiconcave functions u

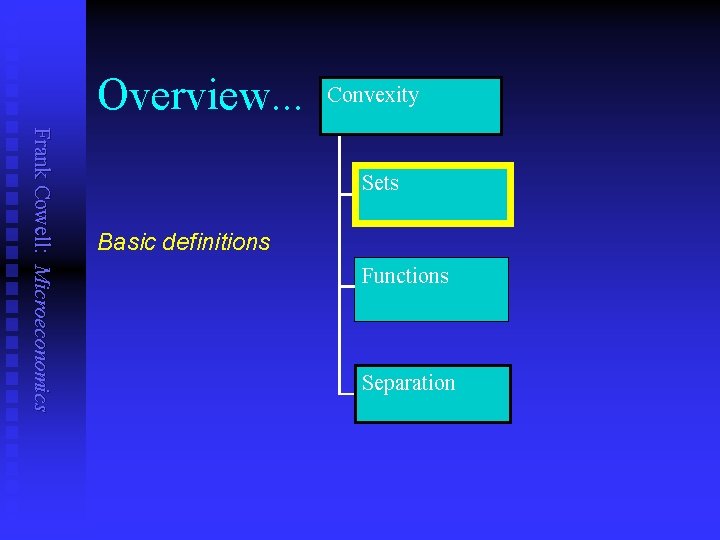
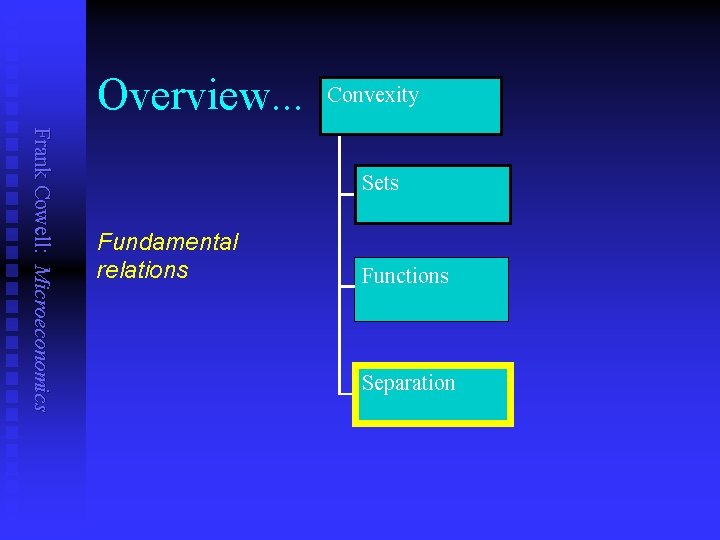
Overview. . . Convexity Frank Cowell: Microeconomics Sets Basic definitions Functions Separation

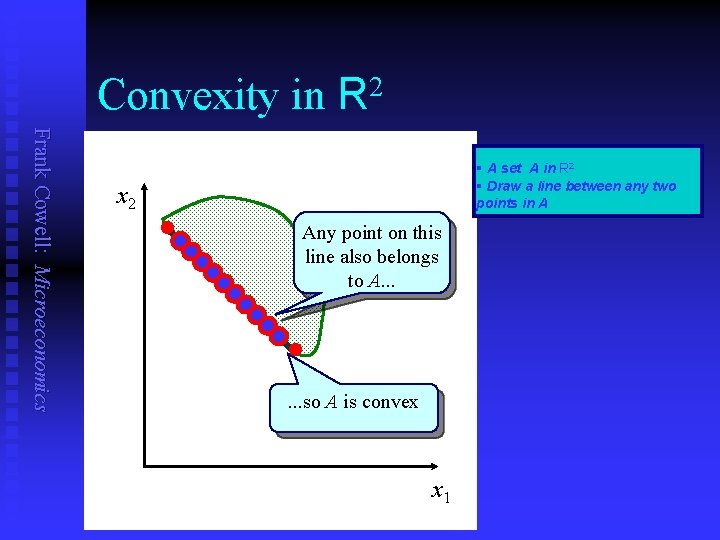
Convexity in 2 R Frank Cowell: Microeconomics § A set A in R 2 § Draw a line between any two points in A x 2 l Any point on this line also belongs to A. . . l. . . so A is convex x 1

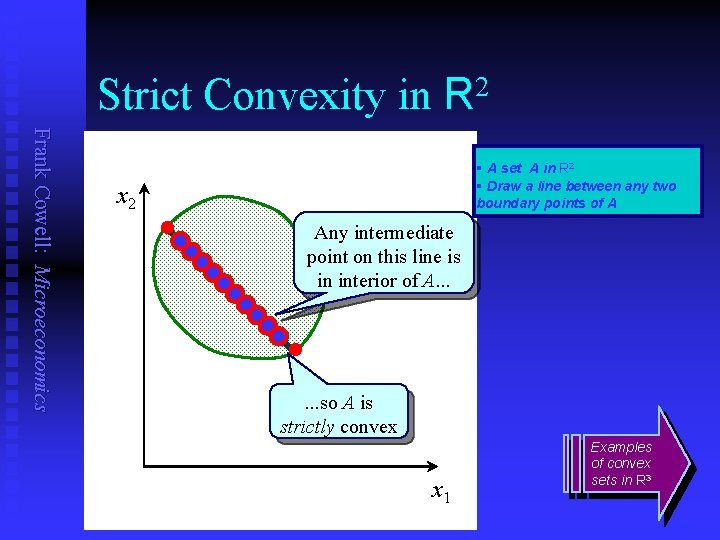
Strict Convexity in 2 R Frank Cowell: Microeconomics § A set A in R 2 § Draw a line between any two boundary points of A x 2 l Any intermediate point on this line is in interior of A. . . l. . . so A is strictly convex x 1 Examples of convex sets in R 3

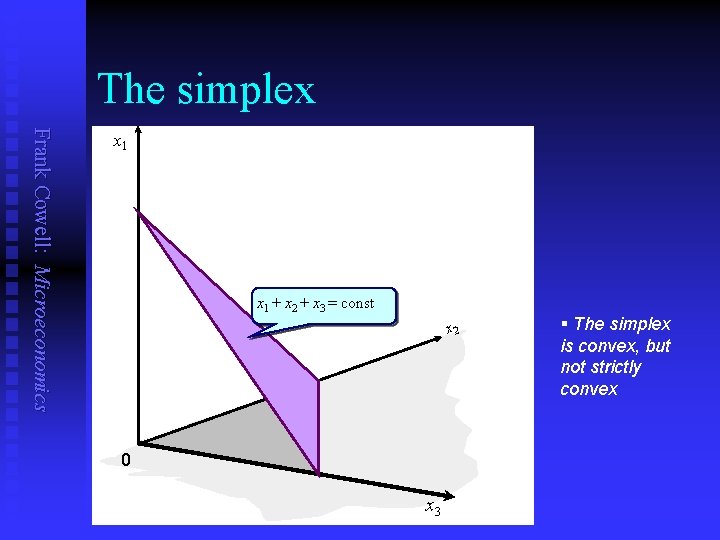
The simplex Frank Cowell: Microeconomics x 1 + x 2 + x 3 = const x 2 0 x 3 § The simplex is convex, but not strictly convex

The ball Frank Cowell: Microeconomics x 1 Si [xi– ai]2 § A ball centred on the point (a 1, a 2, a 3) >0 = const x 2 0 x 3 §It is strictly convex

Overview. . . Convexity Frank Cowell: Microeconomics Sets For scalars and vectors Functions Separation

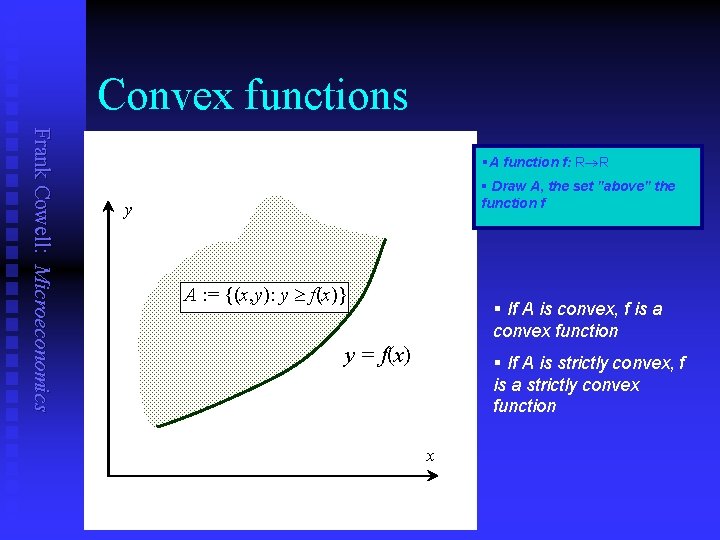
Convex functions Frank Cowell: Microeconomics §A function f: R R § Draw A, the set "above" the function f y A : = {(x, y): y f(x)} § If A is convex, f is a convex function y = f(x) § If A is strictly convex, f is a strictly convex function x

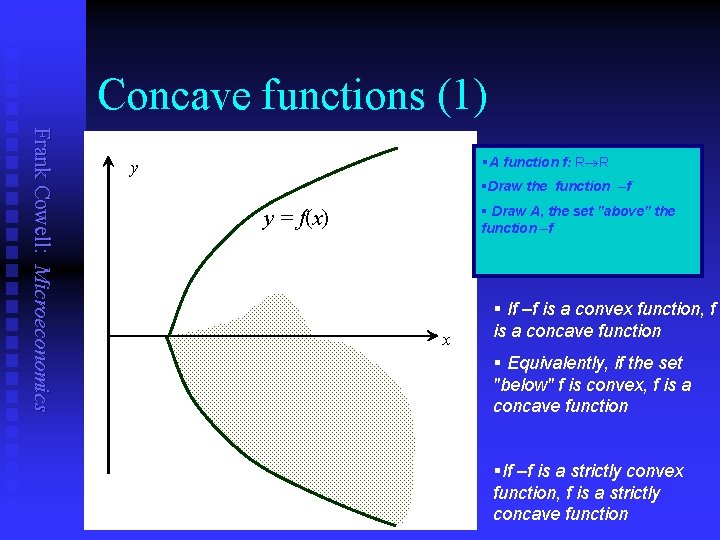
Concave functions (1) Frank Cowell: Microeconomics §A function f: R R y §Draw the function –f § Draw A, the set "above" the function –f y = f(x) x § If –f is a convex function, f is a concave function § Equivalently, if the set "below" f is convex, f is a concave function §If –f is a strictly convex function, f is a strictly concave function

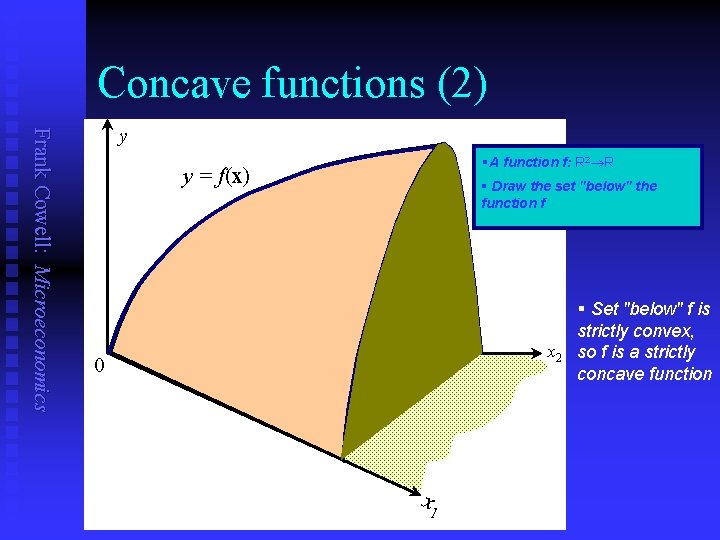
Concave functions (2) Frank Cowell: Microeconomics y §A function f: R 2 R y = f(x) § Draw the set "below" the function f x 2 0 x 1 § Set "below" f is strictly convex, so f is a strictly concave function

Convex and concave function Frank Cowell: Microeconomics y y = f(x) §An affine function f: R R § Draw the set "above" the function f § Draw the set "below" the function f § The graph in R 2 is a straight line. x § Both "above" and “below" sets are convex. §So f is both concave and convex. § Corresponding graph in R 3 would be a plane. §The graph in Rn would be a hyperplane.

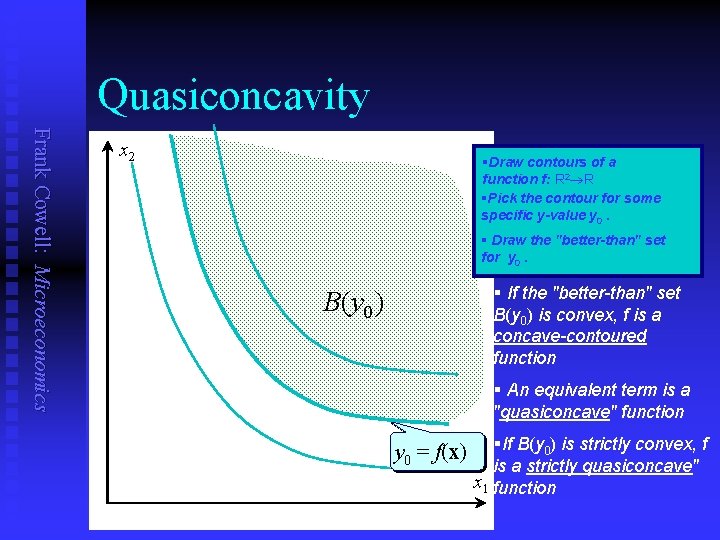
Quasiconcavity Frank Cowell: Microeconomics x 2 §Draw contours of a function f: R 2 R §Pick the contour for some specific y-value y 0. § Draw the "better-than" set for y 0. § If the "better-than" set B(y 0) is convex, f is a concave-contoured function B(y 0) § An equivalent term is a "quasiconcave" function y 0 = f(x) §If B(y 0) is strictly convex, f is a strictly quasiconcave" x 1 function

Overview. . . Convexity Frank Cowell: Microeconomics Sets Fundamental relations Functions Separation

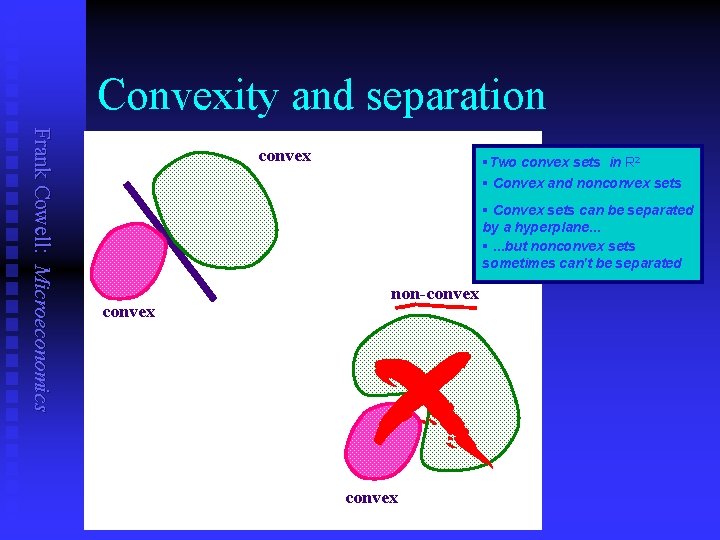
Convexity and separation Frank Cowell: Microeconomics convex §Two convex sets in R 2 § Convex and nonconvex sets § Convex sets can be separated by a hyperplane. . . §. . . but nonconvex sets sometimes can't be separated convex non-convex

A hyperplane in 2 R §Hyperplane in R 2 is a straight line {x: Si pixi c} §Parameters p and c determine the slope and position §Draw in points "above" H H( §Draw in points "below" H : = c) p, : S {x i p xi i =c } Frank Cowell: Microeconomics x 2 {x: Si pixi c} x 1

A hyperplane separating A and y Frank Cowell: Microeconomics x 2 §A convex set A H §A point y "outside" A l §The point x* in A that is closest to y y §The separating hyperplane A l x* § y A. § y lies in the "above-H" set § x* lies in the "below-H" set x 1

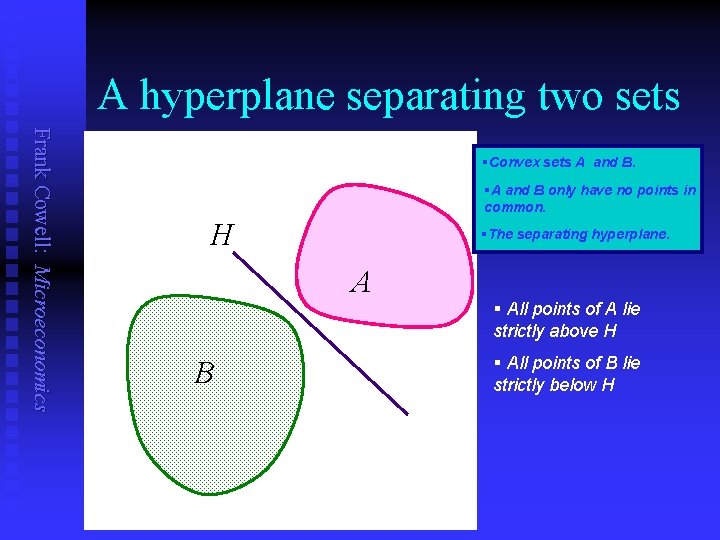
A hyperplane separating two sets Frank Cowell: Microeconomics §Convex sets A and B. §A and B only have no points in common. H §The separating hyperplane. A B § All points of A lie strictly above H § All points of B lie strictly below H

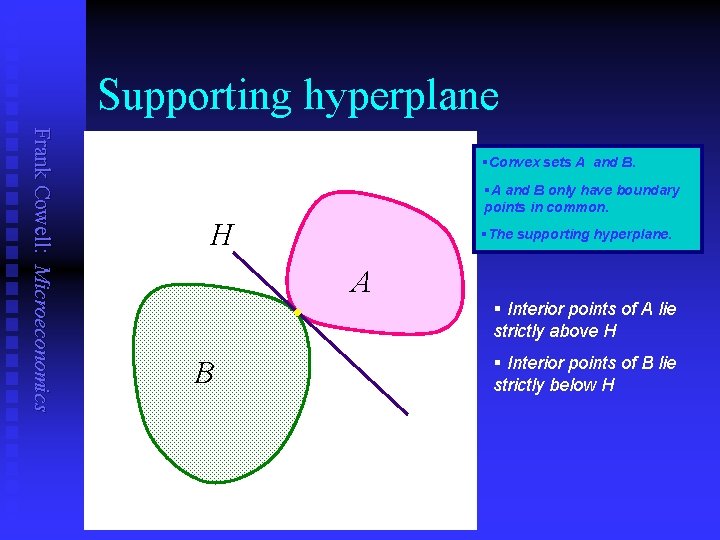
Supporting hyperplane Frank Cowell: Microeconomics §Convex sets A and B. §A and B only have boundary points in common. H §The supporting hyperplane. A l B § Interior points of A lie strictly above H § Interior points of B lie strictly below H