Frank Cowell Microeconomics August 2006 Distributions MICROECONOMICS Principles

Frank Cowell: Microeconomics August 2006 Distributions MICROECONOMICS Principles and Analysis Frank Cowell

Purpose Frank Cowell: Microeconomics n This presentation concerns statistical distributions in microeconomics u u n Distributions make regular appearances in u u n n a brief introduction it does not pretend to generality models involving uncertainty representation of aggregates strategic behaviour empirical estimation methods Certain concepts and functional forms appear regularly We will introduce basic concepts and some key examples

Ingredients of a probability model Frank Cowell: Microeconomics n The variate u u n The support of the distribution u u n could be a scalar – income, family size… Could be a vector – basket of consumption, list of inputs The smallest closed set W whose complement has probability zero A convenient way of specifying clearly what is logically feasible (points in the support) and infeasible (other points). Distribution function u u Captures the probability concept in a convenient and general way Encompass both discrete and continuous distributions.

Discrete and continuous Frank Cowell: Microeconomics n Discrete distributions u u n Continuous distributions u u n W is usually a finite collection of points W could also be countably infinite for univariate distributions S is usually an interval on the real line… … could be bounded or unbounded for multivariate distributions usually a connected subset of real space if F is differentiable on W then define the density function f as the derivative of F Take some particular cases: a collection of examples

Some examples Frank Cowell: Microeconomics n Begin with two cases of discrete distributions u u n Then two simple examples of continuous distributions with bounded support u u n where the variate can take just one of two values where it can take one of five values. The rectangular distribution – uniform density over an interval. Beta distribution – a single-peaked distribution. Finally a standard example of a continuous distribution with unbounded support: u Lognormal distribution

Examples 1 & 2 Frank Cowell: Microeconomics n n Discrete distributions W is the set {x 0, x 1, …, x -1} u u n Example 1 u u n is number of elements in the support assumed positive, finite = 2. Probability p of value x 0; probability 1–p of value x 1. Example 2 u u =5 Probability pi of value xi, i = 0, . . . , 4.
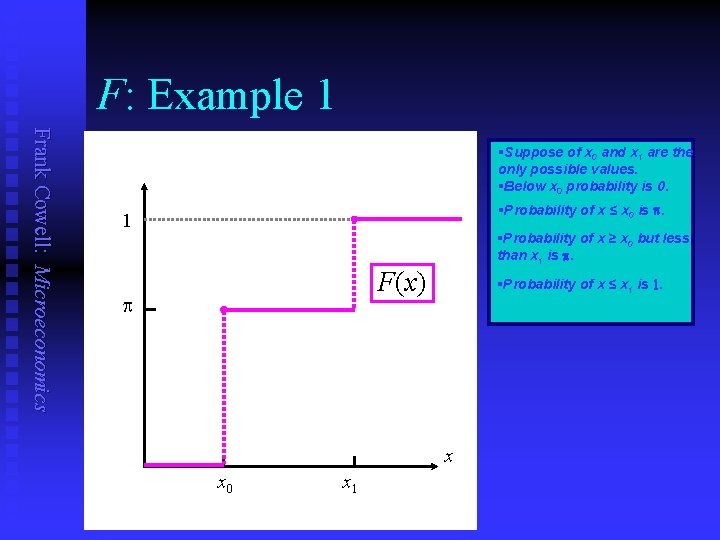
F: Example 1 Frank Cowell: Microeconomics §Suppose of x 0 and x 1 are the only possible values. §Below x 0 probability is 0. §Probability of x ≤ x 0 is p. 1 §Probability of x ≥ x 0 but less than x 1 is p. F(x) p §Probability of x ≤ x 1 is 1. x x 0 x 1
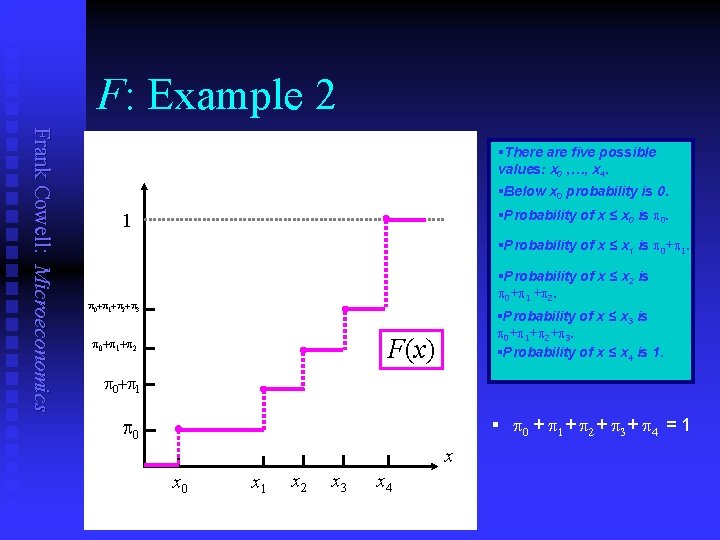
F: Example 2 Frank Cowell: Microeconomics §There are five possible values: x 0 , …, x 4. §Below x 0 probability is 0. §Probability of x ≤ x 0 is p 0. 1 §Probability of x ≤ x 1 is p 0+p 1. §Probability of x ≤ x 2 is p 0+p 1 +p 2. p 0+p 1+p 2+p 3 §Probability of x ≤ x 3 is p 0+p 1+p 2+p 3. §Probability of x ≤ x 4 is 1. F(x) p 0+p 1+p 2 p 0+p 1 § p 0 + p 1 + p 2 + p 3 + p 4 = 1 p 0 x x 0 x 1 x 2 x 3 x 4

Examples 3 & 4 Frank Cowell: Microeconomics n n Continuous distributions In both cases W is the interval [x 0 , x 1 ] u u n Example 3 u u n where x 0 is non-negative… … and x 1 is finite F is differentiable, so… …density f is defined rectangular distribution f(x) = 1 / [ x 1− x 0 ] Example 4 u u Beta distribution [x 0, x 1] = [0, 1]
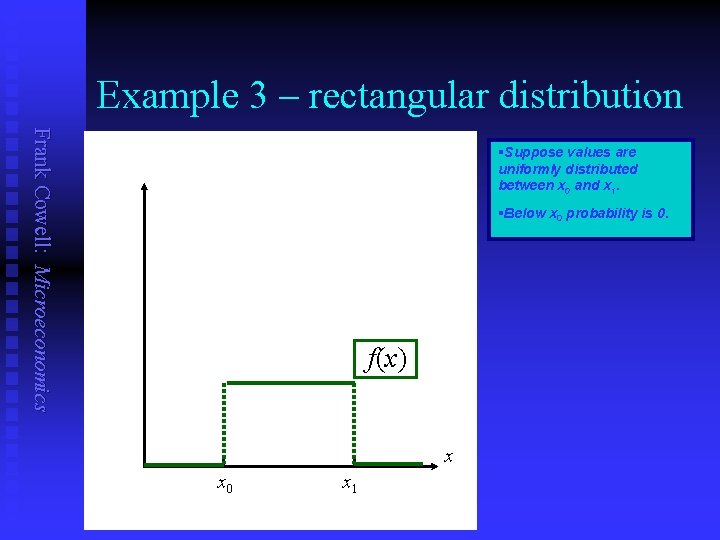
Example 3 – rectangular distribution Frank Cowell: Microeconomics §Suppose values are uniformly distributed between x 0 and x 1. §Below x 0 probability is 0. f(x) x x 0 x 1
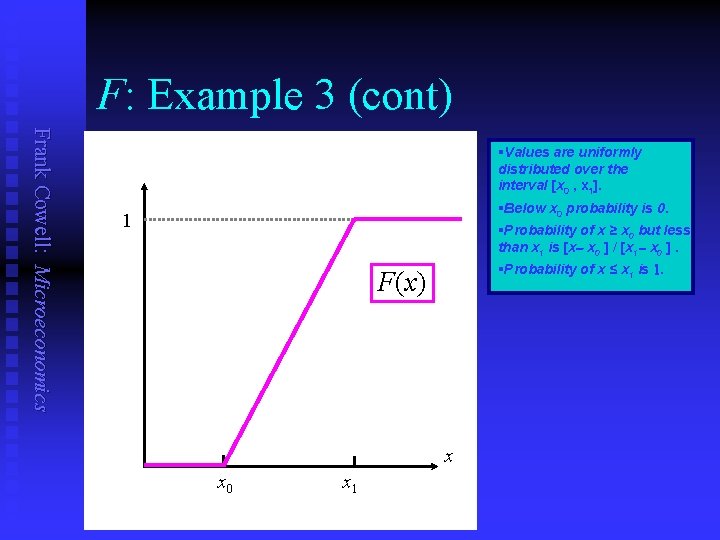
F: Example 3 (cont) Frank Cowell: Microeconomics §Values are uniformly distributed over the interval [x 0 , x 1]. §Below x 0 probability is 0. §Probability of x ≥ x 0 but less than x 1 is [x x 0 ] / [x 1 x 0 ]. 1 §Probability of x ≤ x 1 is 1. F(x) x x 0 x 1
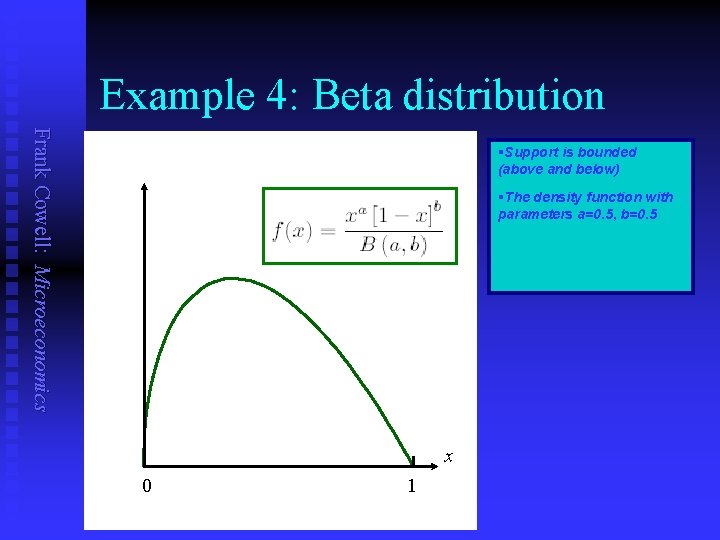
Example 4: Beta distribution Frank Cowell: Microeconomics §Support is bounded (above and below) §The density function with parameters a=0. 5, b=0. 5 x 0 1
![Beta distribution (cont) Frank Cowell: Microeconomics §Support is bounded in [0, 1] §The distribution Beta distribution (cont) Frank Cowell: Microeconomics §Support is bounded in [0, 1] §The distribution](http://slidetodoc.com/presentation_image_h/02a8a4ac7b4460ec58c101dad132754f/image-13.jpg)
Beta distribution (cont) Frank Cowell: Microeconomics §Support is bounded in [0, 1] §The distribution function with parameters a=0. 5, b=0. 5 1 0 0 1

Example 5 Frank Cowell: Microeconomics n Lognormal distribution u Continuous n Unbounded support n W is the interval [0, ∞) F is differentiable, so… u …density f is defined u
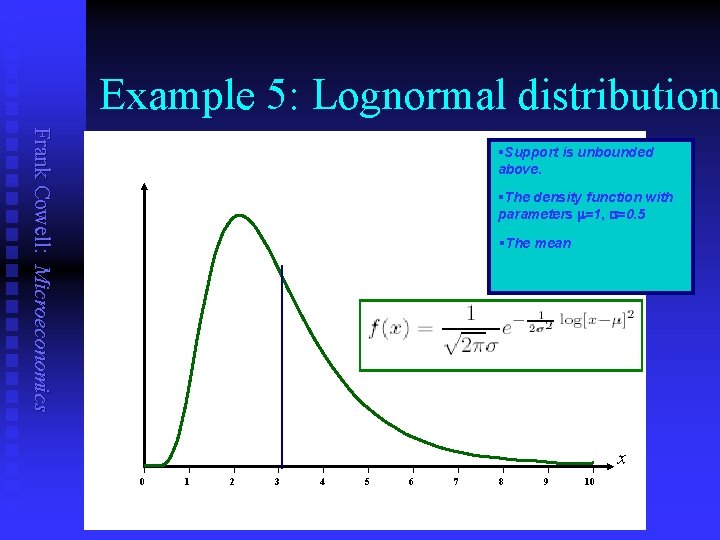
Example 5: Lognormal distribution Frank Cowell: Microeconomics §Support is unbounded above. §The density function with parameters m=1, s=0. 5 §The mean x 0 1 2 3 4 5 6 7 8 9 10
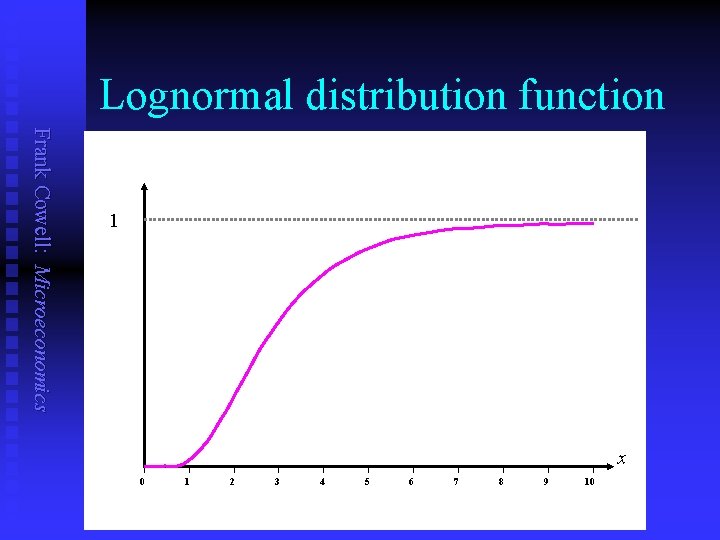
Lognormal distribution function Frank Cowell: Microeconomics 1 x 0 1 2 3 4 5 6 7 8 9 10
- Slides: 16