Francesco Leonetti Compressione frattale di immagini scanner Compressione

scanner Compressione delle immagini compressione frattale di immagini

Triangolo di Sierpinski simulazioni di Demba Diallo Mady

b G G(b) G(a) a X X allora f=G(f) G f X G(f) X

x(1)=d, x(2)=G(d), x(3)=G(G(d)), . . . x(1) x(2) x(n) x(3) X f x(n) è

X = insieme di tutte le figure = G: X eccetera X è definita

a G(a) = V 1(a) G(a) V 2(a) V 3(a) a V 1(a) a

f come figura 80 pixel x 80 pixel necessita di 6400 parametri f come

f = G(f) = V 1(f) V 2(f) V 3(f) V 1(f) V 2(f)

Data una immagine i trovare trasformazioni W 1 , W 2 , … ,

Esempio Data l’immagine i allora i = W 1(i) W 2(i) W 3(i) W

Decompressione L(a) = W 2 (a R 1) W 3 (a R 2) W

Barnsley M - Hurd L, Fractal image compression, 1993 Fisher Y, Fractal image compression:

leonetti@univaq. it http: //univaq. it/~leonetti

Slides: 67

Download presentation

Francesco Leonetti Compressione frattale di immagini

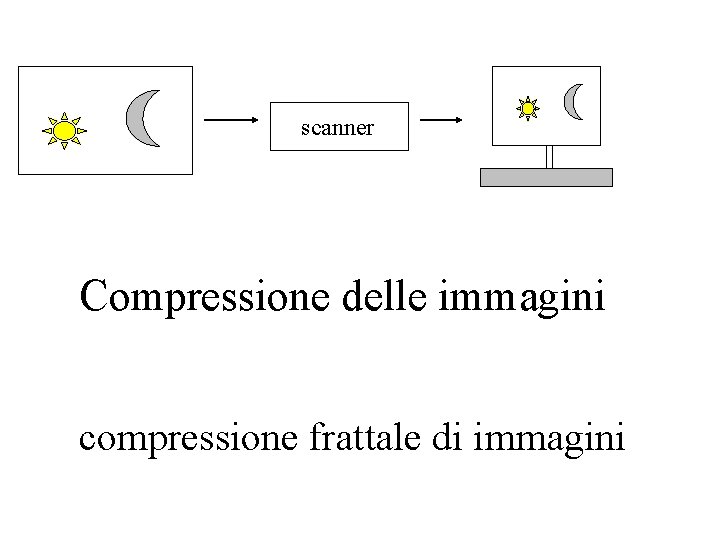
scanner Compressione delle immagini compressione frattale di immagini

FRATTALI Figure frastagliate

Curva di Koch

Triangolo di Sierpinski

Triangolo di Sierpinski simulazioni di Demba Diallo Mady

b G G(b) G(a) a X X allora f=G(f) G f X G(f) X

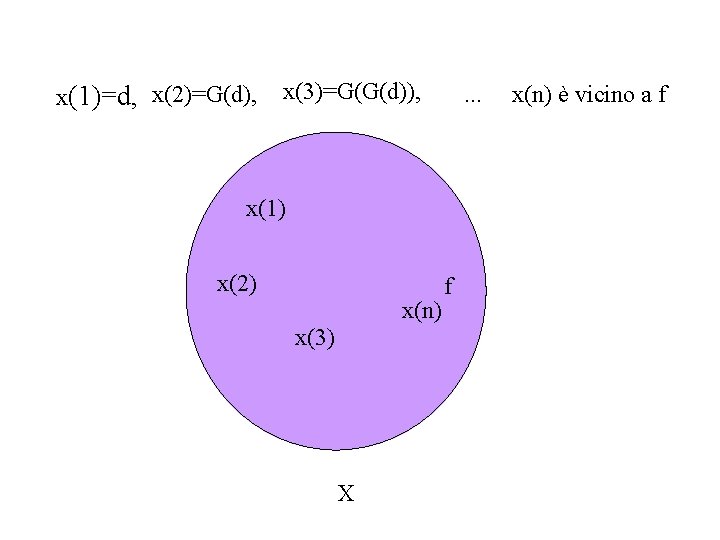
x(1)=d, x(2)=G(d), x(3)=G(G(d)), . . . x(1) x(2) x(n) x(3) X f x(n) è vicino a f

X = insieme di tutte le figure = G: X eccetera X è definita così Da qualunque figura si parta, applicando ripetutamente G, si arriva alla figura f che non è cambiata da G: f=G(f)

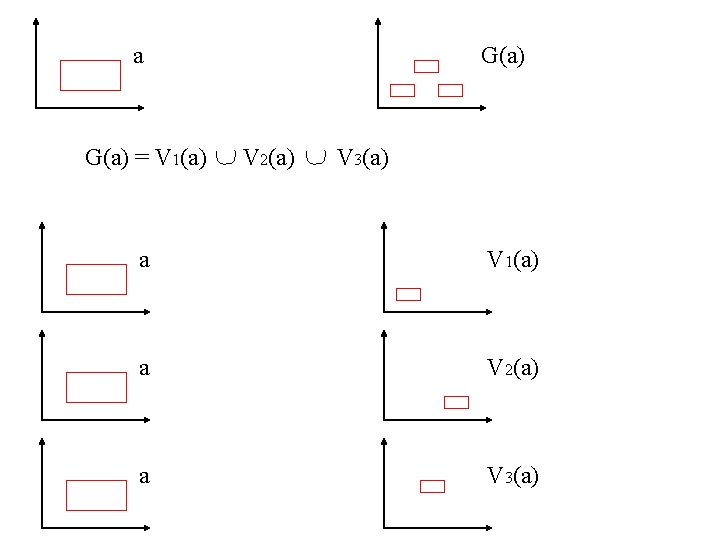
a G(a) = V 1(a) G(a) V 2(a) V 3(a) a V 1(a) a V 2(a) a V 3(a)

S 1/2 (x , y) = (x/2 , y/2) T u , v (x , y) = (x+u , y+v) V 1 = T 0 , 0 V 2 = T 40 , 0 ° S 1/2 V 3 = T 20 , ( )20 ° S 1/2 G(a) = V 1(a) V 2(a) V 3(a) G necessita di 9 parametri

f come figura 80 pixel x 80 pixel necessita di 6400 parametri f come unica figura fissa di G necessita dei soli parametri di G: 9 parametri Compressione = 6400 / 9 = 711

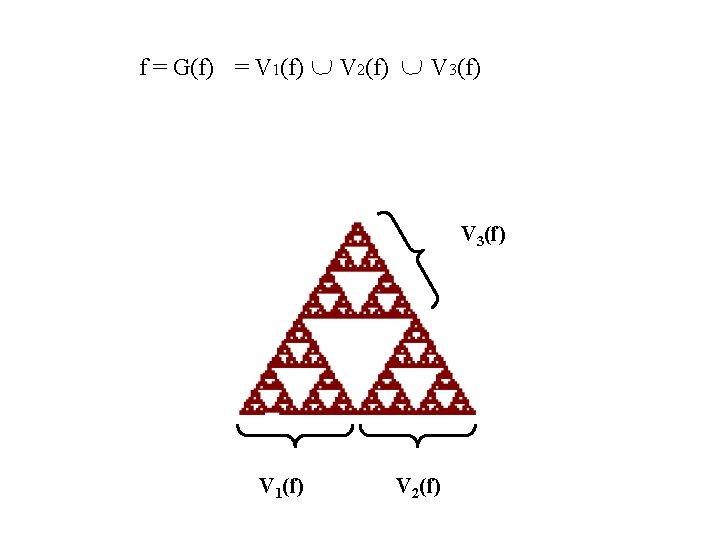
f = G(f) = V 1(f) V 2(f) V 3(f) V 1(f) V 2(f)

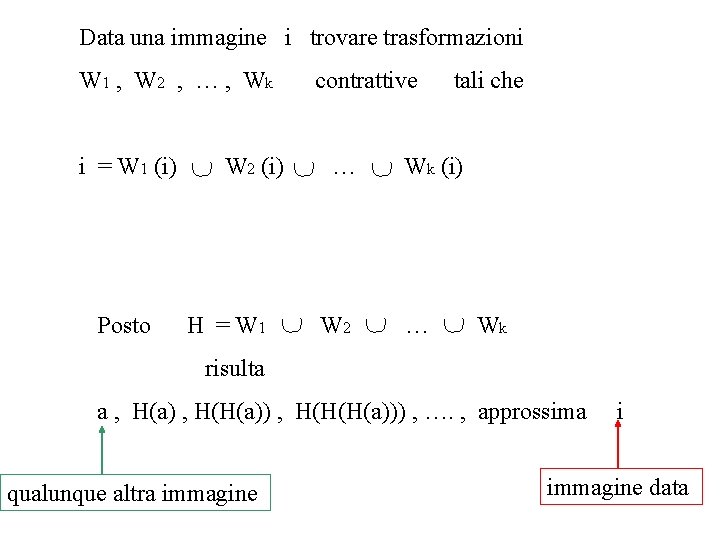
Data una immagine i trovare trasformazioni W 1 , W 2 , … , Wk i = W 1 (i) Posto W 2 (i) H = W 1 contrattive … W 2 tali che Wk (i) … Wk risulta a , H(a) , H(H(a)) , H(H(H(a))) , …. , approssima qualunque altra immagine i immagine data

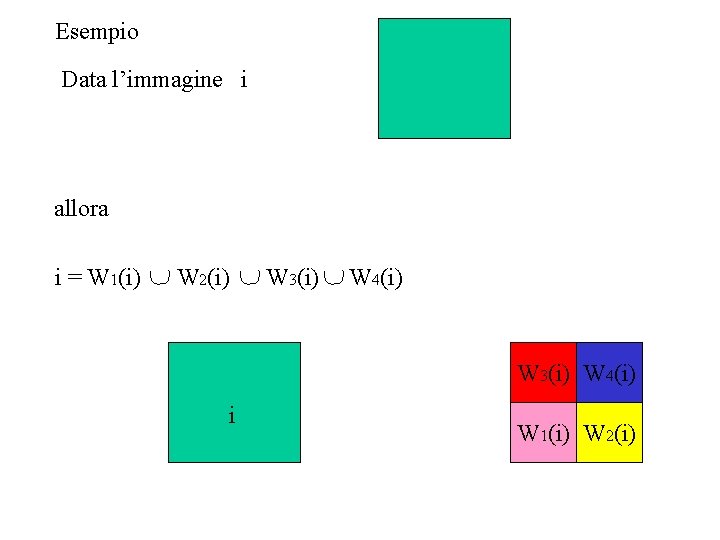
Esempio Data l’immagine i allora i = W 1(i) W 2(i) W 3(i) W 4(i) i W 1(i) W 2(i)

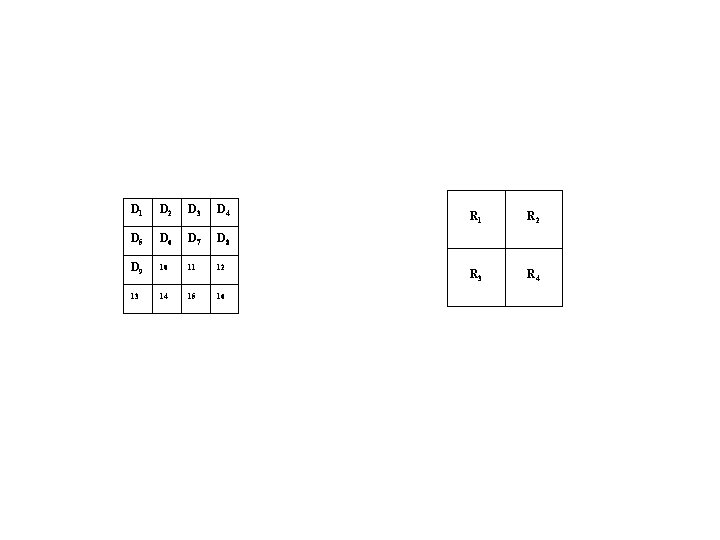
D 1 D 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 10 11 12 13 14 15 16 R 1 R 2 R 3 R 4

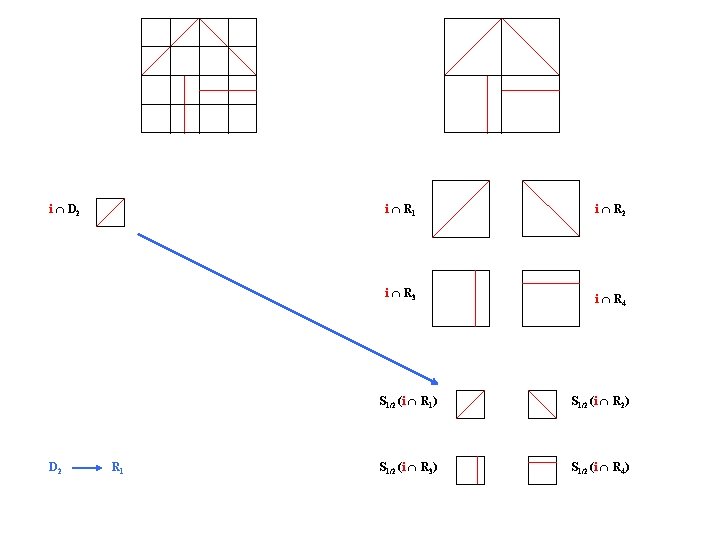
i D 2 R 1 i R 2 i R 3 i R 4 S 1/2 (i R 1) S 1/2 (i R 2) S 1/2 (i R 3) S 1/2 (i R 4)

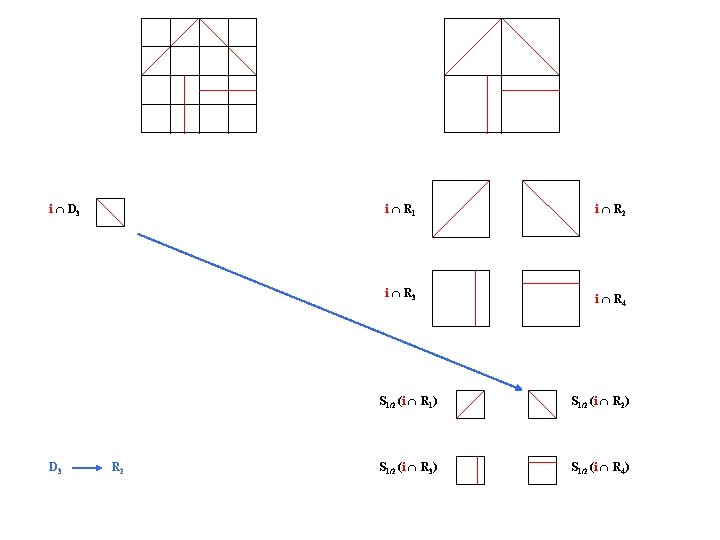
i D 3 R 2 i R 1 i R 2 i R 3 i R 4 S 1/2 (i R 1) S 1/2 (i R 2) S 1/2 (i R 3) S 1/2 (i R 4)

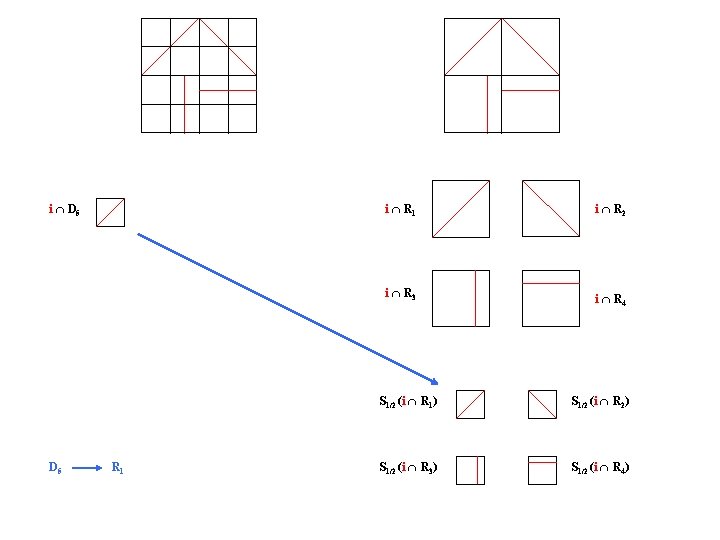
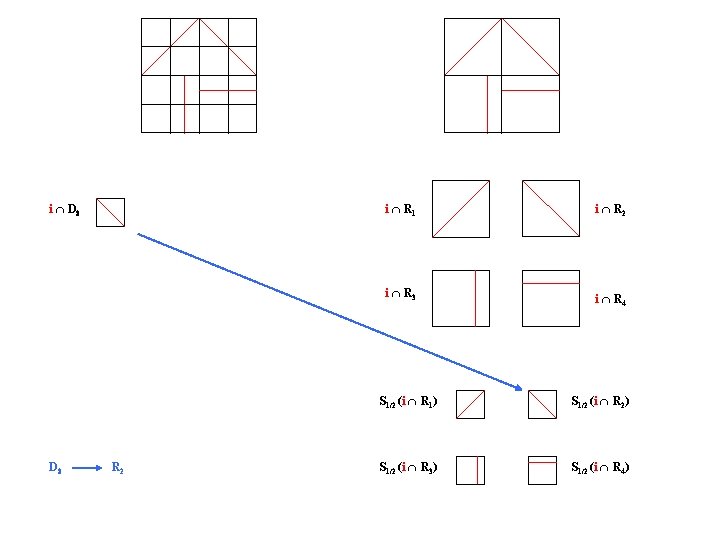
i D 5 R 1 i R 2 i R 3 i R 4 S 1/2 (i R 1) S 1/2 (i R 2) S 1/2 (i R 3) S 1/2 (i R 4)

i D 8 R 2 i R 1 i R 2 i R 3 i R 4 S 1/2 (i R 1) S 1/2 (i R 2) S 1/2 (i R 3) S 1/2 (i R 4)

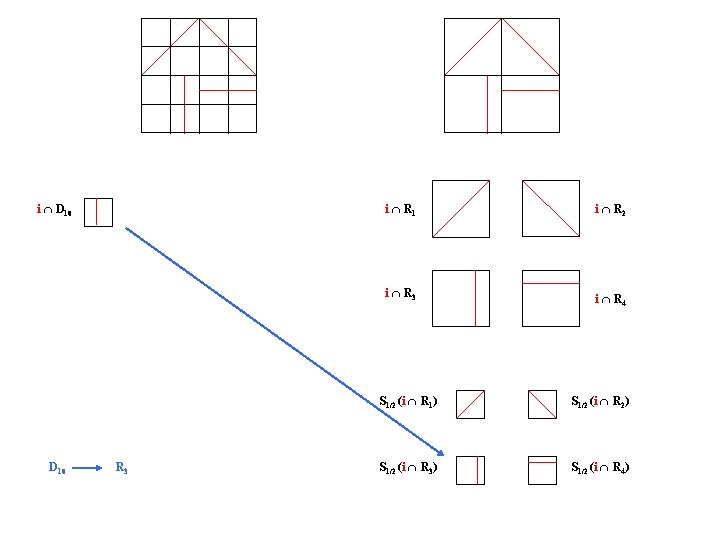
i D 10 R 3 i R 1 i R 2 i R 3 i R 4 S 1/2 (i R 1) S 1/2 (i R 2) S 1/2 (i R 3) S 1/2 (i R 4)

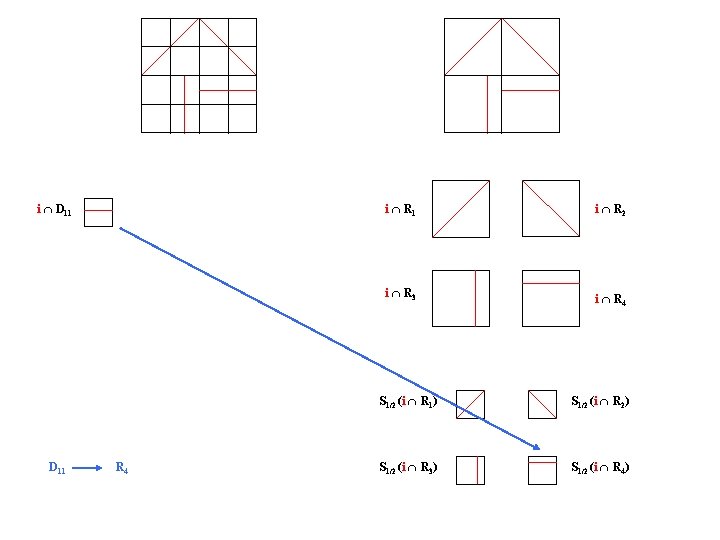
i D 11 R 4 i R 1 i R 2 i R 3 i R 4 S 1/2 (i R 1) S 1/2 (i R 2) S 1/2 (i R 3) S 1/2 (i R 4)

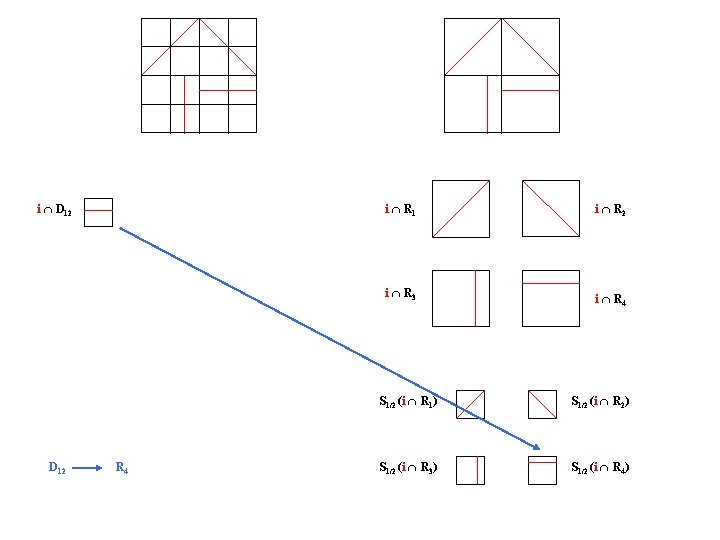
i D 12 R 4 i R 1 i R 2 i R 3 i R 4 S 1/2 (i R 1) S 1/2 (i R 2) S 1/2 (i R 3) S 1/2 (i R 4)

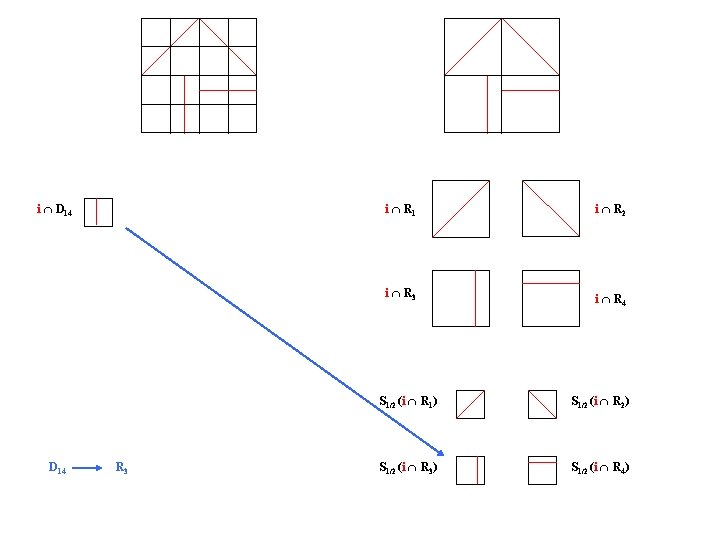
i D 14 R 3 i R 1 i R 2 i R 3 i R 4 S 1/2 (i R 1) S 1/2 (i R 2) S 1/2 (i R 3) S 1/2 (i R 4)

D 2 R 1 2; 1 D 3 R 2 3; 2 D 5 R 1 5; 1 D 8 R 2 8; 2 D 10 R 3 10; 3 D 11 R 4 11; 4 D 12 R 4 12; 4 D 14 R 3 14; 3 L(a) = W 2 (a R 1) W 3 (a R 2) W 5 (a R 1) W 8 (a R 2) W 10 (a R 3) W 11 (a R 4) W 12 (a R 4) W 14 (a R 3) Dj = Tu, v S 1/2 (Rk) Wj = Tu, v S 1/2

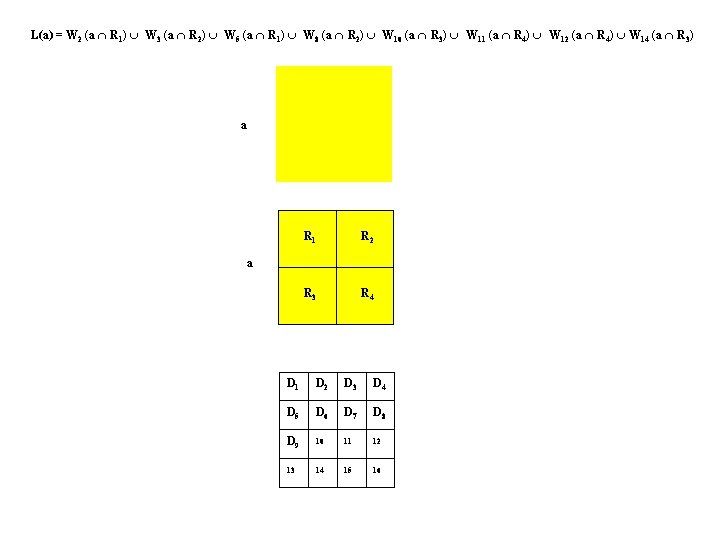
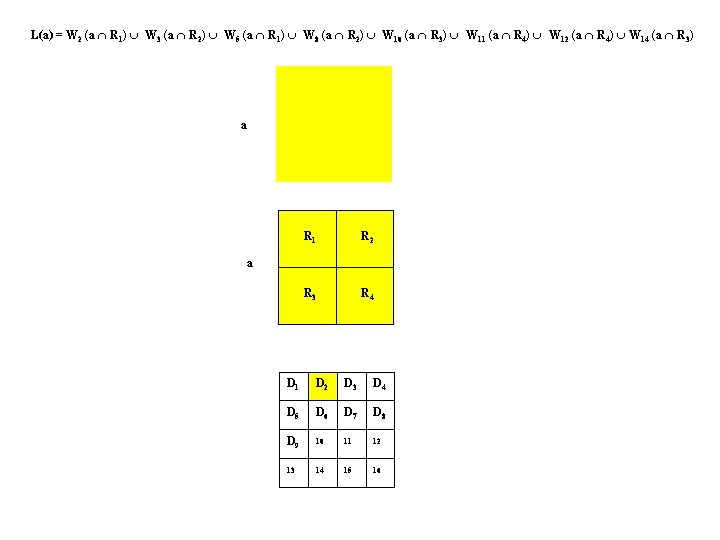
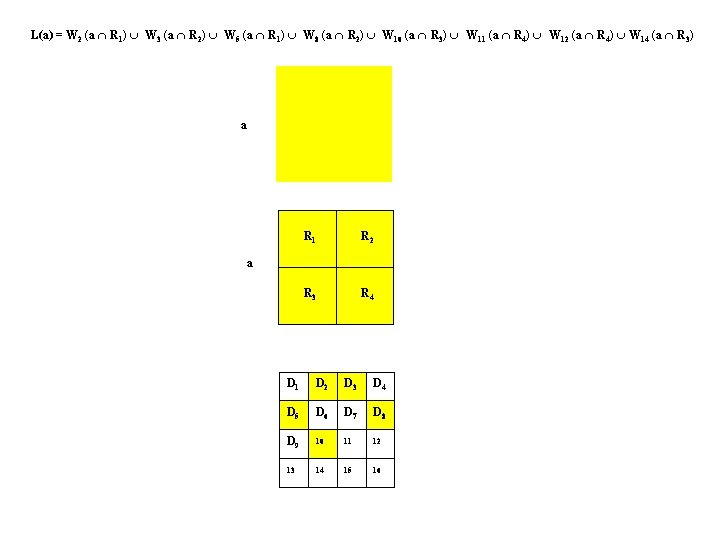
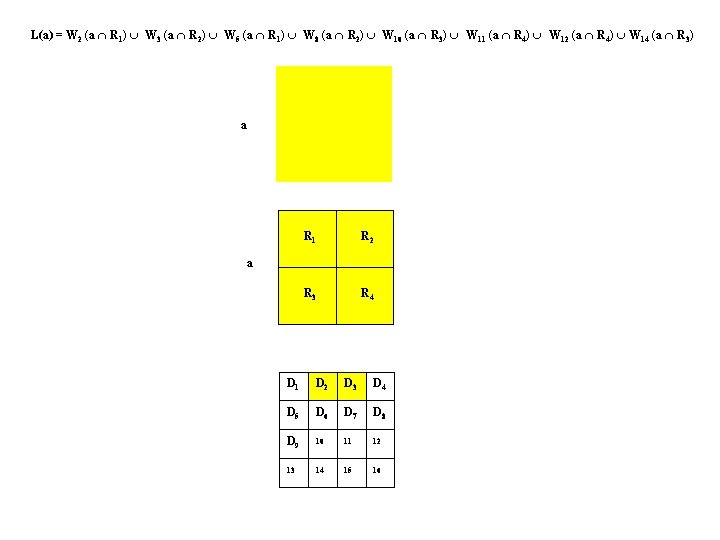
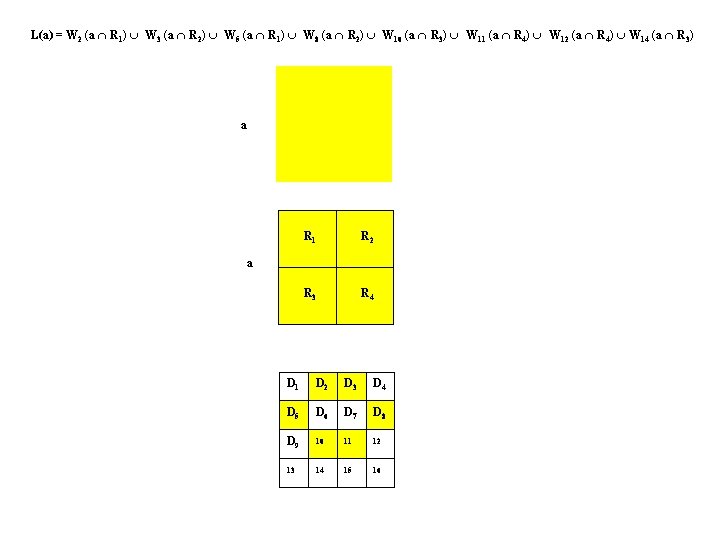
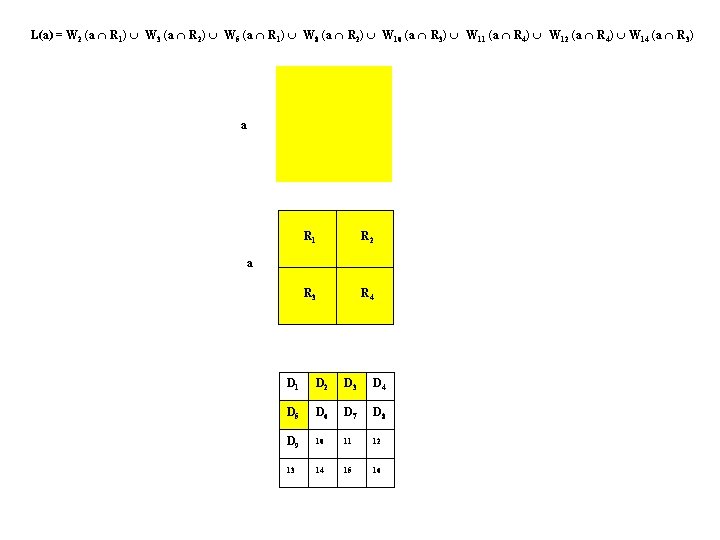
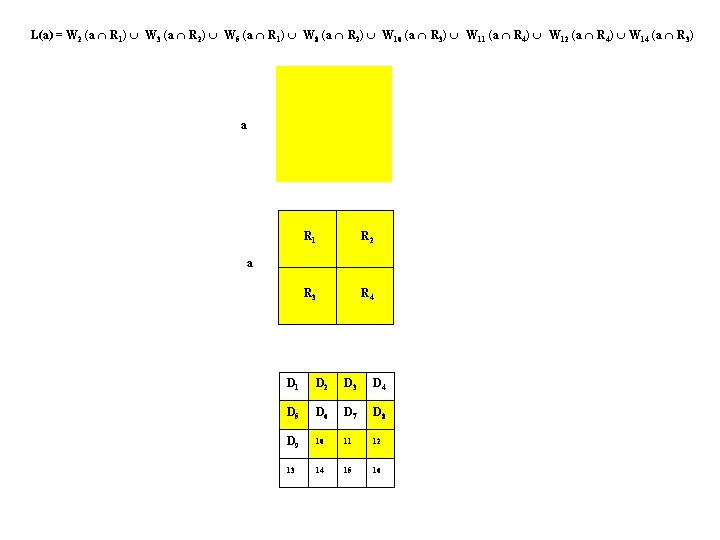
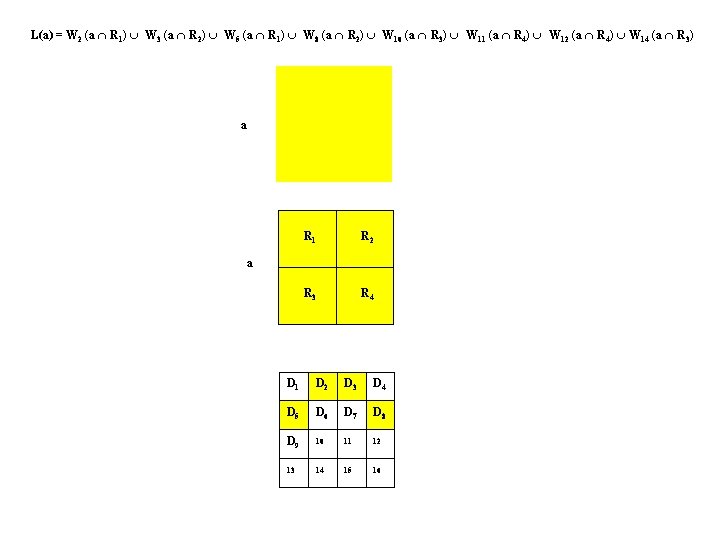
L(a) = W 2 (a R 1) W 3 (a R 2) W 5 (a R 1) W 8 (a R 2) W 10 (a R 3) W 11 (a R 4) W 12 (a R 4) W 14 (a R 3) a R 1 R 2 R 3 R 4 a D 1 D 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 10 11 12 13 14 15 16

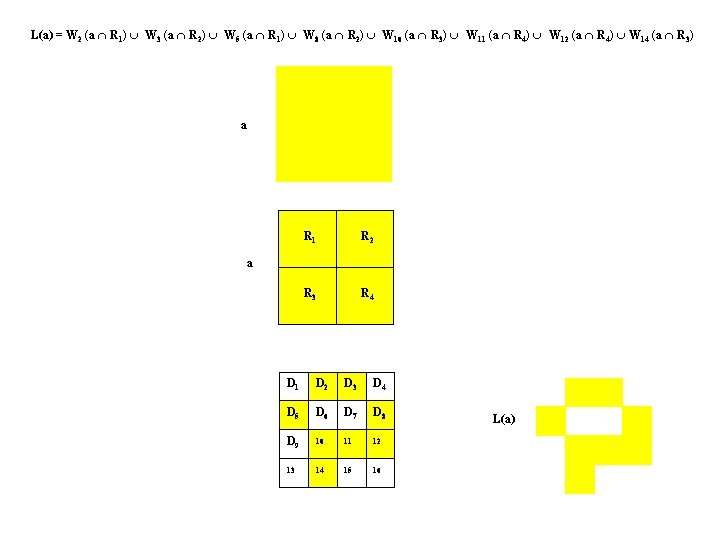
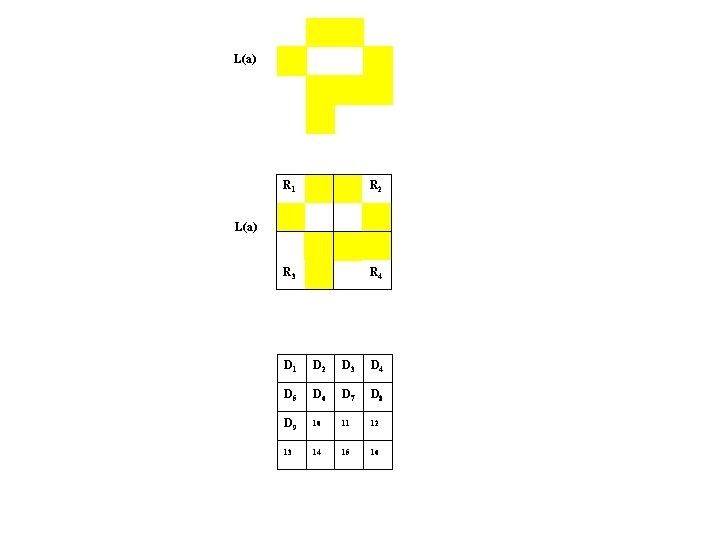
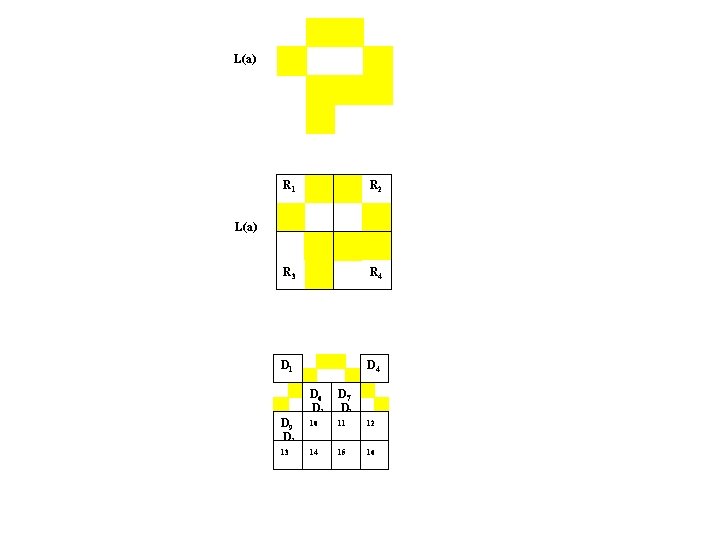
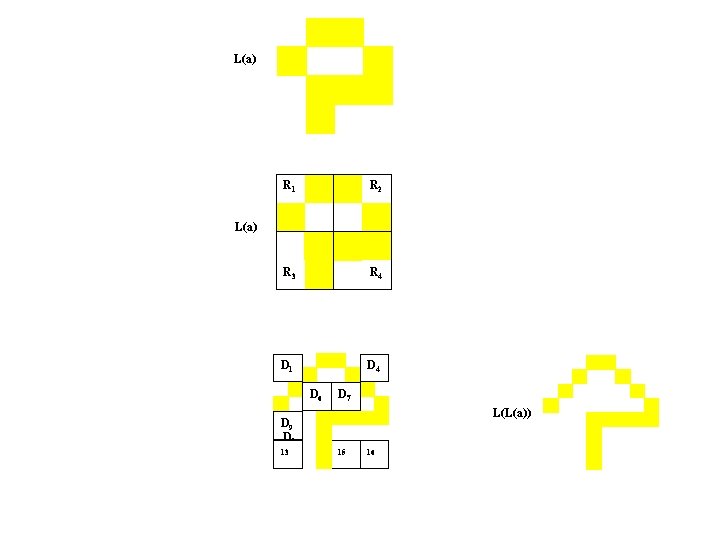
L(a) = W 2 (a R 1) W 3 (a R 2) W 5 (a R 1) W 8 (a R 2) W 10 (a R 3) W 11 (a R 4) W 12 (a R 4) W 14 (a R 3) a R 1 R 2 R 3 R 4 a D 1 D 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 10 11 12 13 14 15 16 L(a)

L(a) R 1 R 2 R 3 R 4 L(a) D 1 D 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 10 11 12 13 14 15 16

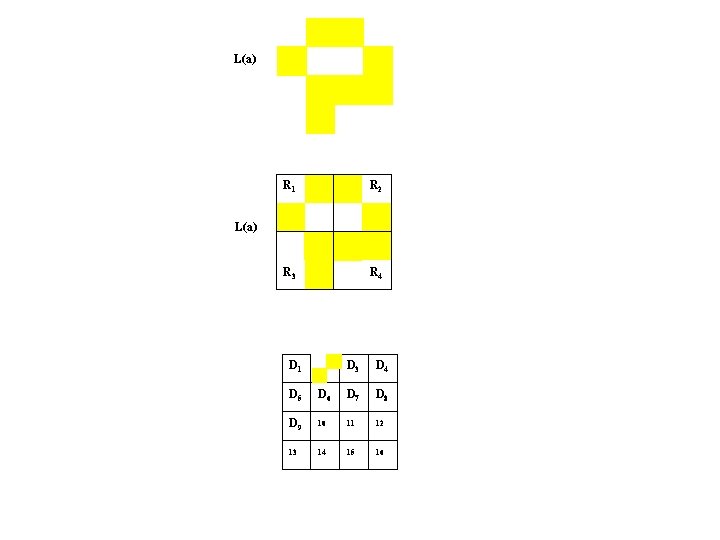
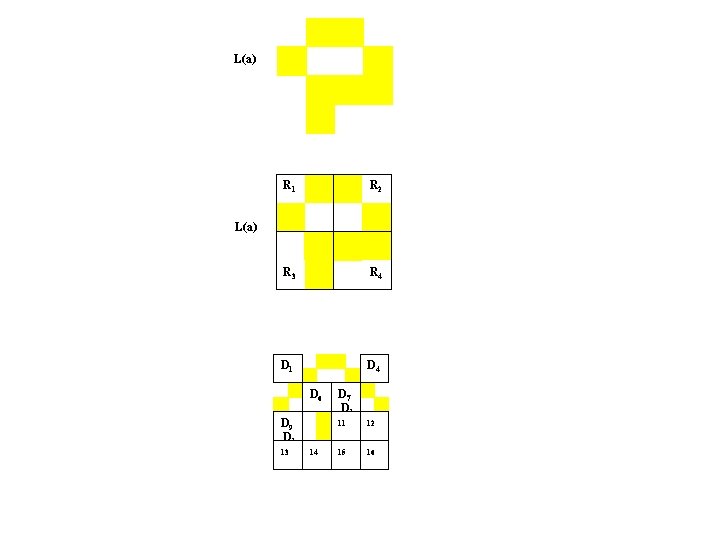
L(a) R 1 R 2 R 3 R 4 L(a) D 1 D 3 D 4 D 5 D 6 D 7 D 8 D 9 10 11 12 13 14 15 16

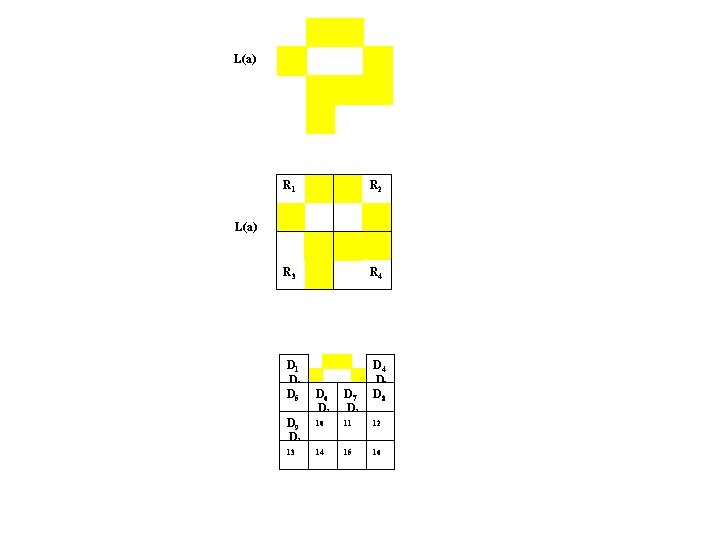
L(a) R 1 R 2 R 3 R 4 L(a) D 1 D 5 D 9 D 1 13 D 4 D 1 D 8 D 6 D 1 D 7 D 1 10 11 12 14 15 16

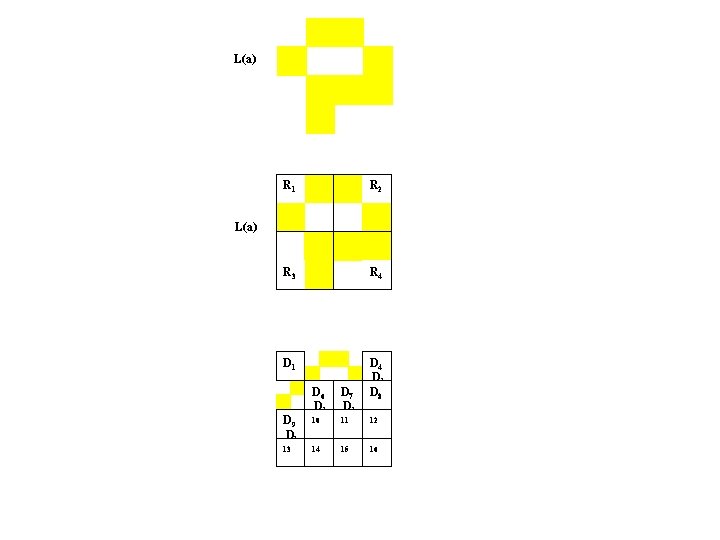
L(a) R 1 R 2 R 3 R 4 D 1 D 8 L(a) D 9 D 1 13 D 6 D 1 D 7 D 1 10 11 12 14 15 16

L(a) R 1 R 2 R 3 R 4 D 1 D 4 L(a) D 9 D 1 13 D 6 D 1 D 7 D 1 10 11 12 14 15 16

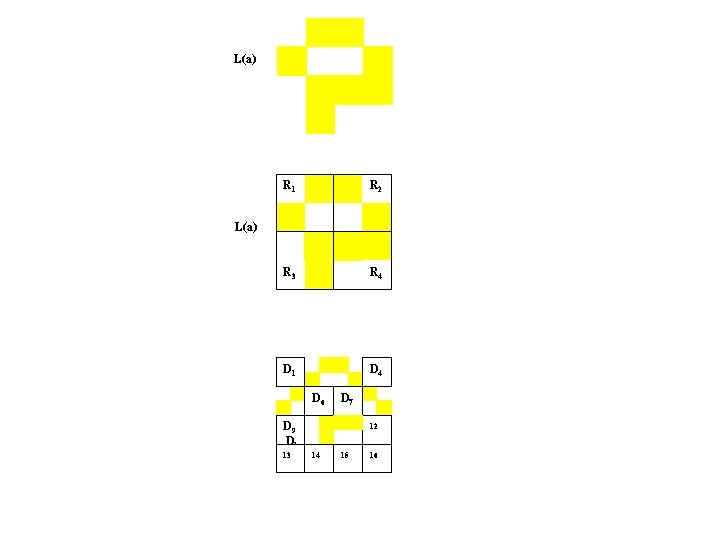
L(a) R 1 R 2 R 3 R 4 D 1 D 4 L(a) D 6 D 9 D 1 13 14 D 7 D 1 11 12 15 16

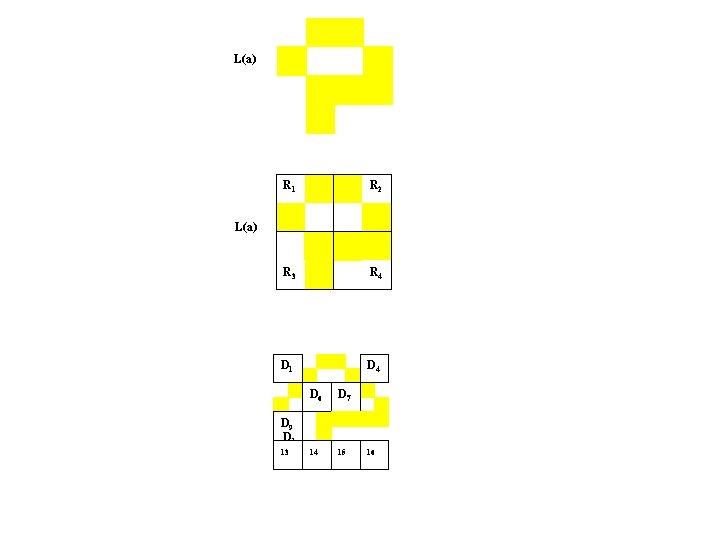
L(a) R 1 R 2 R 3 R 4 D 1 D 4 L(a) D 6 D 7 D 9 D 1 13 12 14 15 16

L(a) R 1 R 2 R 3 R 4 D 1 D 4 L(a) D 6 D 7 14 15 D 9 D 1 13 16

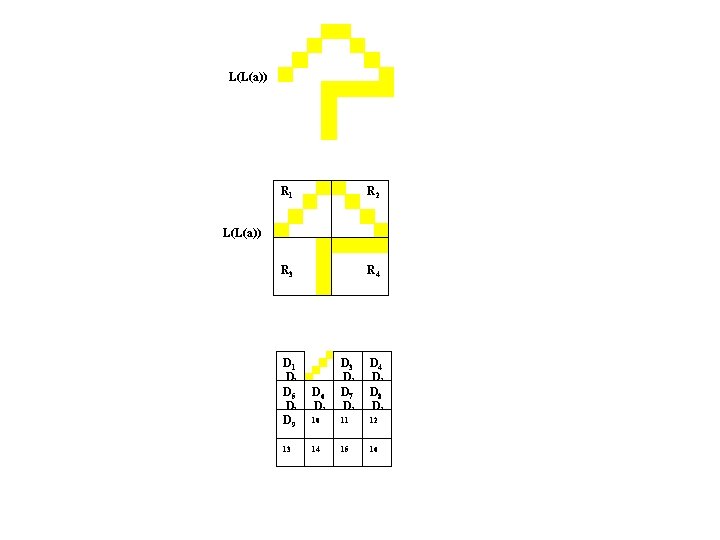
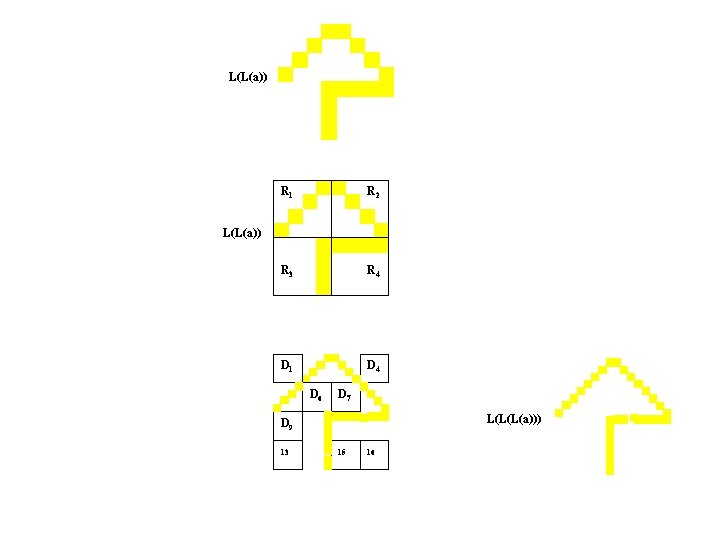
L(a) R 1 R 2 R 3 R 4 D 1 D 4 L(a) D 6 D 7 L(L(a)) D 9 D 1 13 15 16

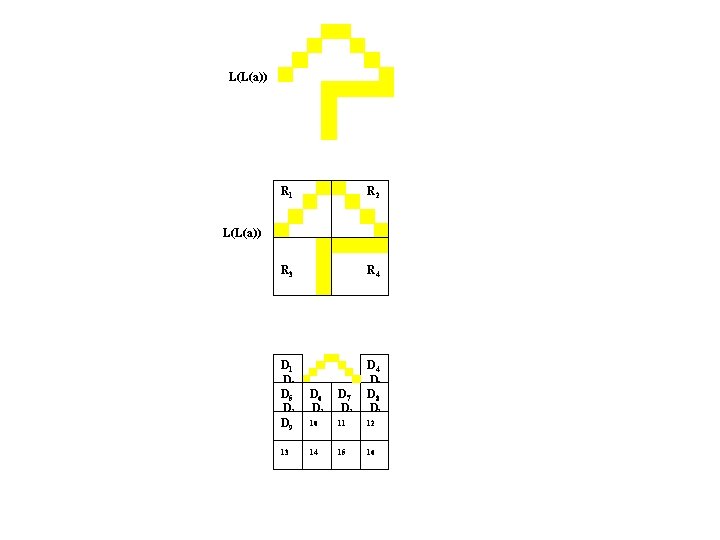
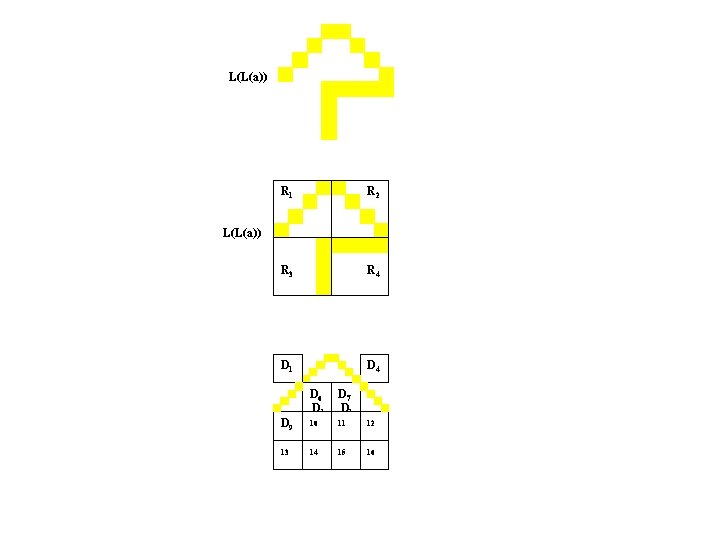
L(L(a)) R 1 R 2 R 3 R 4 L(L(a)) D 1 D 5 D 1 D 9 D 2 D 6 D 1 D 3 D 1 D 7 D 1 D 4 D 1 D 8 D 1 10 11 12 13 14 15 16

L(L(a)) R 1 R 2 R 3 R 4 L(L(a)) D 1 D 5 D 1 D 9 13 D 6 D 1 D 3 D 1 D 7 D 1 D 4 D 1 D 8 D 1 10 11 12 14 15 16

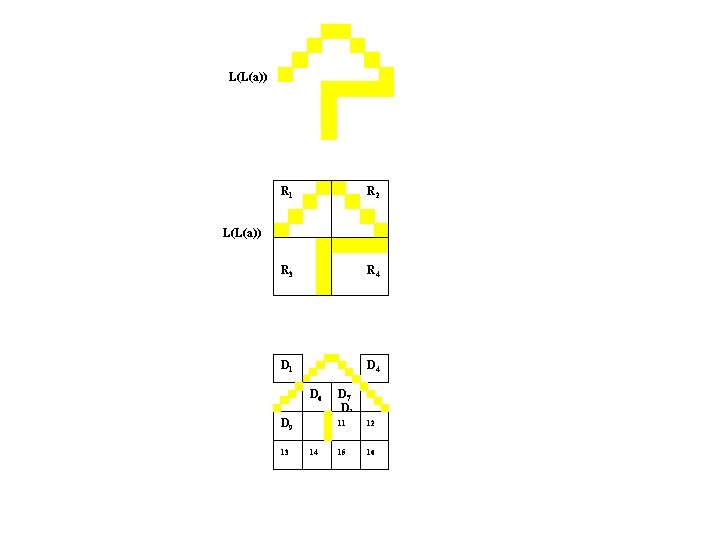
L(L(a)) R 1 R 2 R 3 R 4 D 1 D 5 D 1 D 9 L(L(a)) 13 D 6 D 1 D 7 D 1 D 4 D 1 D 8 D 1 10 11 12 14 15 16

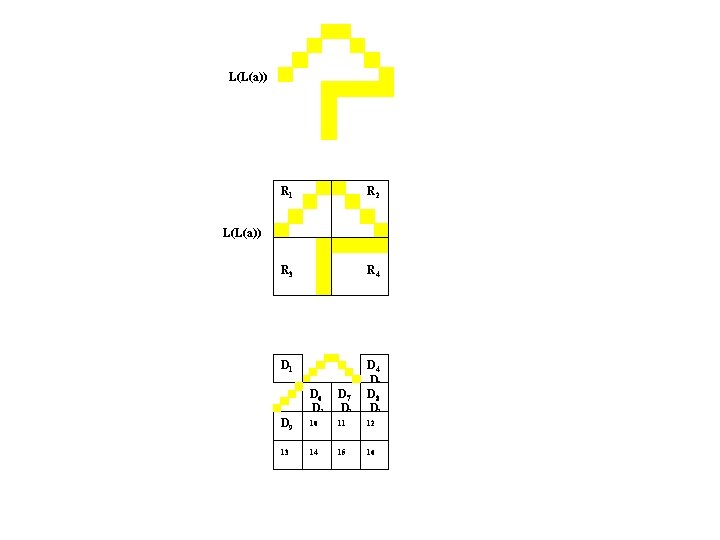
L(L(a)) R 1 R 2 R 3 R 4 D 1 L(L(a)) D 9 13 D 6 D 1 D 7 D 1 D 4 D 1 D 8 D 1 10 11 12 14 15 16

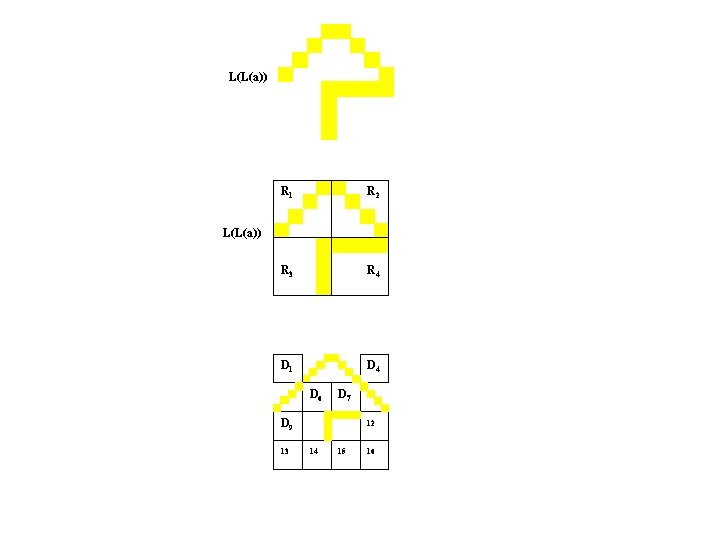
L(L(a)) R 1 R 2 R 3 R 4 D 1 D 4 L(L(a)) D 9 13 D 6 D 1 D 7 D 1 10 11 12 14 15 16

L(L(a)) R 1 R 2 R 3 R 4 D 1 D 4 L(L(a)) D 6 D 9 13 14 D 7 D 1 11 12 15 16

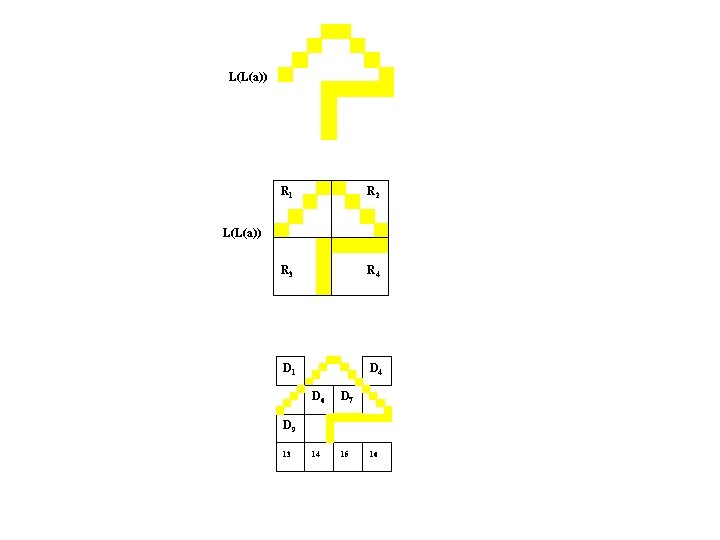
L(L(a)) R 1 R 2 R 3 R 4 D 1 D 4 L(L(a)) D 6 D 7 D 9 13 12 14 15 16

L(L(a)) R 1 R 2 R 3 R 4 D 1 D 4 L(L(a)) D 6 D 7 14 15 D 9 13 16

L(L(a)) R 1 R 2 R 3 R 4 D 1 D 4 L(L(a)) D 6 D 7 L(L(L(a))) D 9 13 15 16

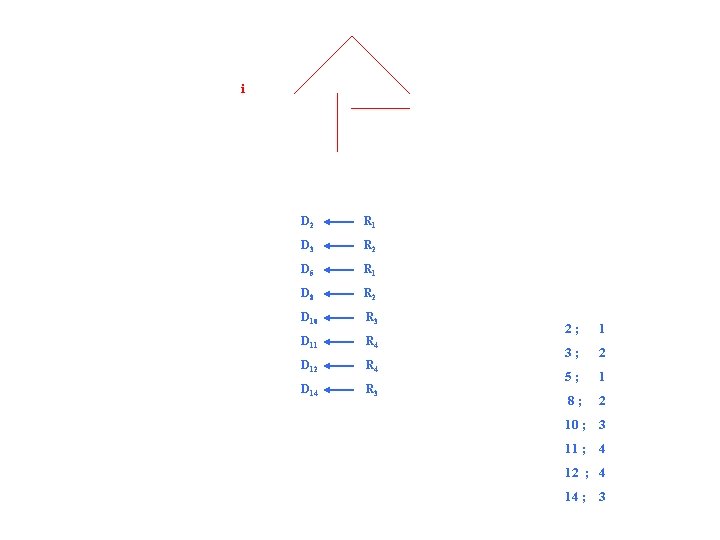
i D 2 R 1 D 3 R 2 D 5 R 1 D 8 R 2 D 10 R 3 D 11 R 4 D 12 R 4 D 14 R 3 2; 1 3; 2 5; 1 8; 2 10 ; 3 11 ; 4 12 ; 4 14 ; 3

1; 0 2; 1 3; 2 4; 0 5; 1 6; 0 7; 0 8; 2 9; 0 10 ; 3 11 ; 4 12 ; 4 13 ; 0 14 ; 3 15 ; 0 16 ; 0 Compressione: 6400/16 = 400

Decompressione L(a) = W 2 (a R 1) W 3 (a R 2) W 5 (a R 1) W 8 (a R 2) W 10 (a R 3) W 11 (a R 4) W 12 (a R 4) W 14 (a R 3)

Decompressione L(a) = W 2 (a R 1) W 3 (a R 2) W 5 (a R 1) W 8 (a R 2) W 10 (a R 3) W 11 (a R 4) W 12 (a R 4) W 14 (a R 3) a

Decompressione L(a) = W 2 (a R 1) W 3 (a R 2) W 5 (a R 1) W 8 (a R 2) W 10 (a R 3) W 11 (a R 4) W 12 (a R 4) W 14 (a R 3) a L(a)

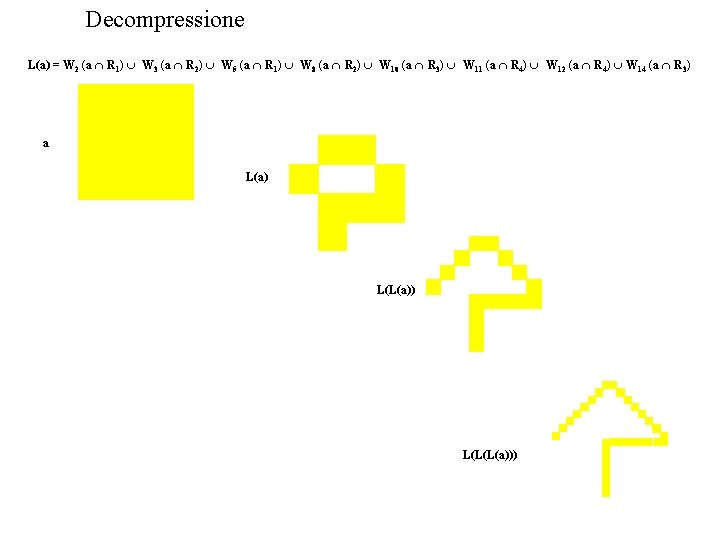
Decompressione L(a) = W 2 (a R 1) W 3 (a R 2) W 5 (a R 1) W 8 (a R 2) W 10 (a R 3) W 11 (a R 4) W 12 (a R 4) W 14 (a R 3) a L(a) L(L(a))

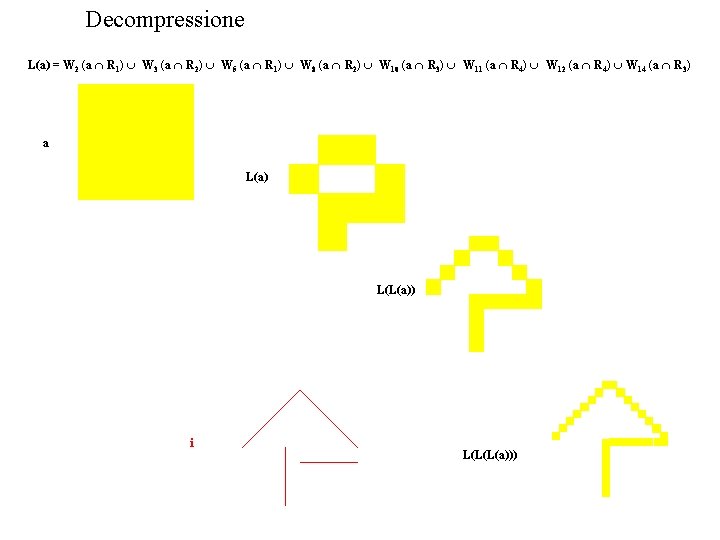
Decompressione L(a) = W 2 (a R 1) W 3 (a R 2) W 5 (a R 1) W 8 (a R 2) W 10 (a R 3) W 11 (a R 4) W 12 (a R 4) W 14 (a R 3) a L(a) L(L(a)) L(L(L(a)))

Decompressione L(a) = W 2 (a R 1) W 3 (a R 2) W 5 (a R 1) W 8 (a R 2) W 10 (a R 3) W 11 (a R 4) W 12 (a R 4) W 14 (a R 3) a L(a) L(L(a)) i L(L(L(a)))

Barnsley M - Hurd L, Fractal image compression, 1993 Fisher Y, Fractal image compression: theory and application to digital images, 1995 http: //www. inf. uni-konstanz. de/cgip/fractal/html/index. html

leonetti@univaq. it http: //univaq. it/~leonetti