Fracture Toughness of Metallic Glasses A DuctiletoBrittle Transition

Fracture Toughness of Metallic Glasses: A Ductile-to-Brittle Transition? Eran Bouchbinder Weizmann Institute of Science Metallic glass (glassy alloy) Work with Chris H. Rycroft University of California, Berkeley Lowhaphandu and Lewandowski Scripta Materialia 38, 1811 (1998)

Strength [MPa] Metallic Glasses Elastic limit [%] Unfortunately, metallic glasses can be extremely brittle

“Ductile” The ability of a material to resist failure in the presence of a crack “Brittle” A single glass under annealing Fracture energy [KJ/m 2] Ductile-to-Brittle transition Poisson’s ratio

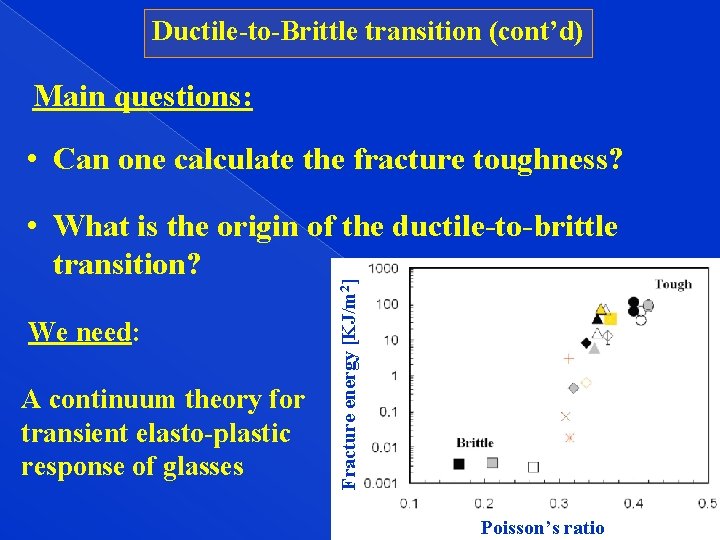
Ductile-to-Brittle transition (cont’d) Main questions: • Can one calculate the fracture toughness? We need: A continuum theory for transient elasto-plastic response of glasses Fracture energy [KJ/m 2] • What is the origin of the ductile-to-brittle transition? Poisson’s ratio

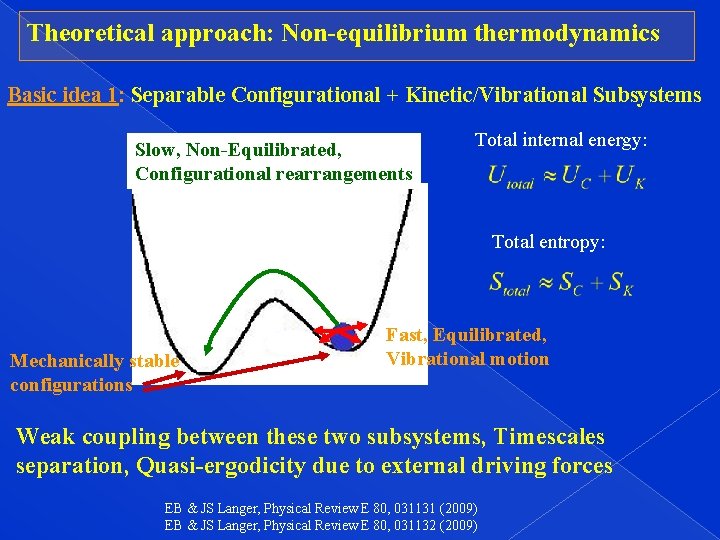
Theoretical approach: Non-equilibrium thermodynamics Basic idea 1: Separable Configurational + Kinetic/Vibrational Subsystems Slow, Non-Equilibrated, Focus on two configurations Configurational rearrangements Total internal energy: Total entropy: Mechanically stable configurations Fast, Equilibrated, Vibrational motion Weak coupling between these two subsystems, Timescales separation, Quasi-ergodicity due to external driving forces EB & JS Langer, Physical Review E 80, 031131 (2009) EB & JS Langer, Physical Review E 80, 031132 (2009)

Basic idea 2: The non-equilibrium state of the system can be characterized by coarse-grained internal variables The elastic part of the deformation A small number of coarse-grained internal variables (order parameters), describe internal degrees of freedom that may be out of equilibrium Non-equilibrium entropy A constrained measure of the number of configurations When in thermodynamic limit EB & JS Langer, Physical Review E 80, 031131 (2009) EB & JS Langer, Physical Review E 80, 031132 (2009)

Basic idea 2: The non-equilibrium state of the system can be (cont’d) characterized by coarse-grained internal variables Define two different temperatures: “Effective” temperature, non-equilibrium degrees of freedom Ordinary, equilibrium temperature Early ideas in the glass/granular materials community: Edwards, Cugliandolo, Kurchan, Coniglio, Barrat, Berthier and more is a true thermodynamic temperature, e. g. it appears in equations of state, it controls the probability of configurational fluctuations etc. Thermodynamic interpretation of soft. Eglassy rheology models EB & JS Langer, Physical Review 80, 031131 (2009) P. Sollich and M. JSE. Cates, Phys. Rev. E 031132 85, 031127 EB & Langer, Physical Review E 80, (2009) (2012)

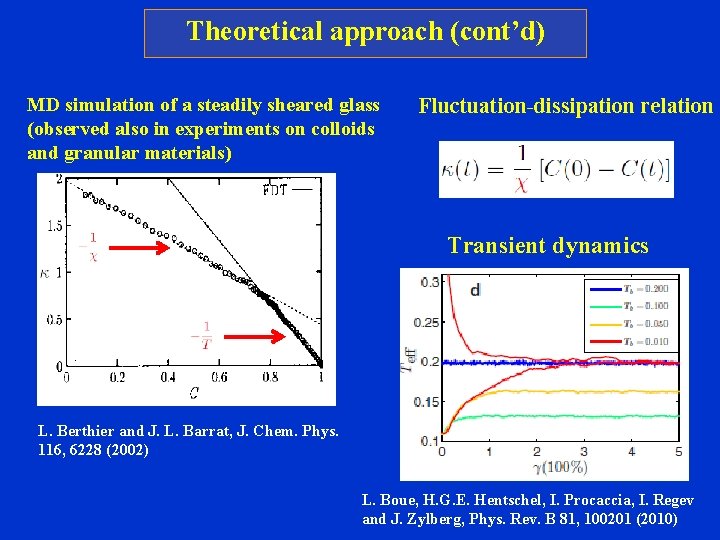
Theoretical approach (cont’d) MD simulation of a steadily sheared glass (observed also in experiments on colloids and granular materials) Fluctuation-dissipation relation Transient dynamics L. Berthier and J. L. Barrat, J. Chem. Phys. 116, 6228 (2002) L. Boue, H. G. E. Hentschel, I. Procaccia, I. Regev and J. Zylberg, Phys. Rev. B 81, 100201 (2010)

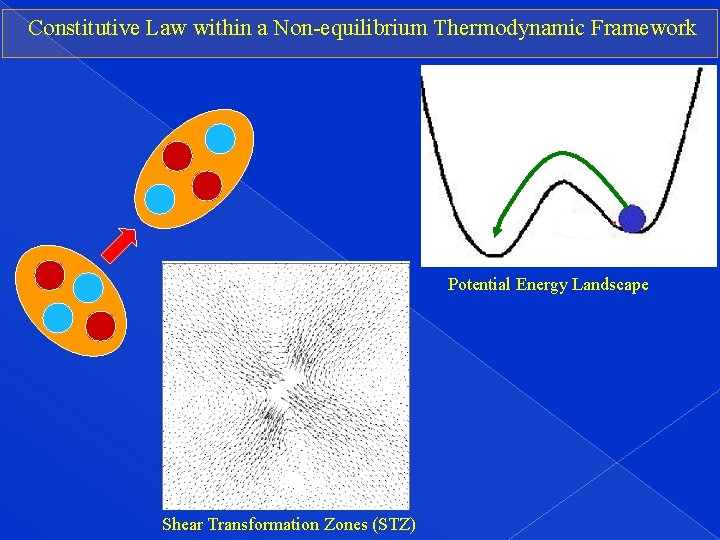
Constitutive Law within a Non-equilibrium Thermodynamic Framework Potential Energy Landscape Shear Transformation Zones (STZ)

Constitutive Law (cont’d) Shear Transformation Zones (STZ) model Two steps: Step 1 – Identify internal state variables and associate with them energy and entropy Step 2 – Develop equations of motion consistent with the laws of thermodynamics Assumptions: • Solid-like starting point • Dilute distribution of soft spots of two-level nature • Mean field Falk & JS Langer, Physical Review E 57, 7192 (1998) EB, JS Langer & I Procaccia, Physical Review E 75, 036107 (2007) EB & JS Langer, Physical Review E 80, 031133 (2009) ML Falk & JS Langer, Annu. Rev. Condens. Matter Phys. 2, 353 (2011)

Constitutive Law (cont’d) Shear Transformation Zones (STZ) model STZ flips + STZ creation - STZ annihilation

The Equations Plastic flow law: Kinematics: Hooke’s law: Force balance:

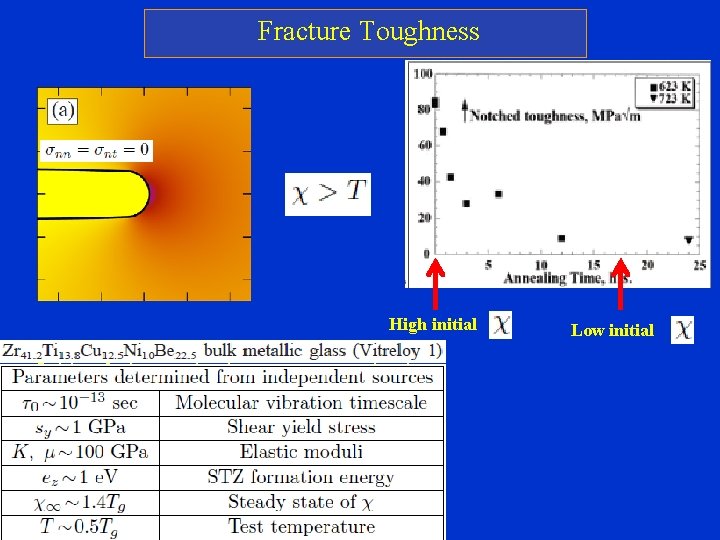
Fracture Toughness High initial K-fields of Linear Elastic Fracture Mechanics ( Universal r-1/2 stress singularity) Low initial

Computational challenges Tracking free-boundaries motion Imposing realistic loading rates

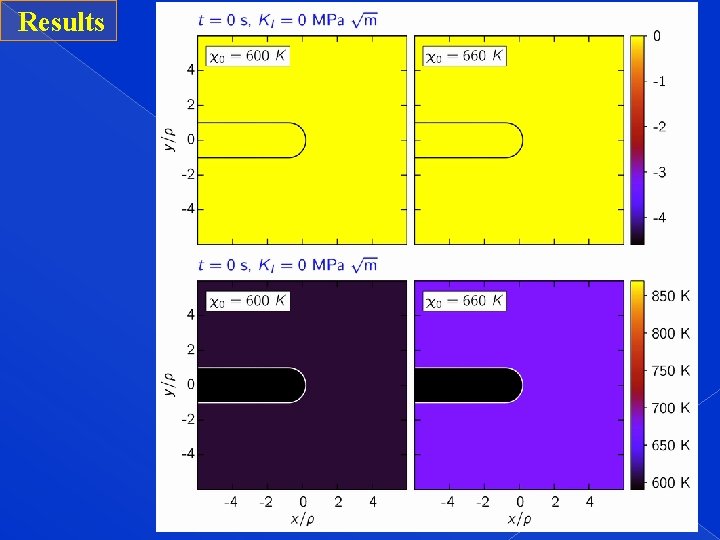
Results

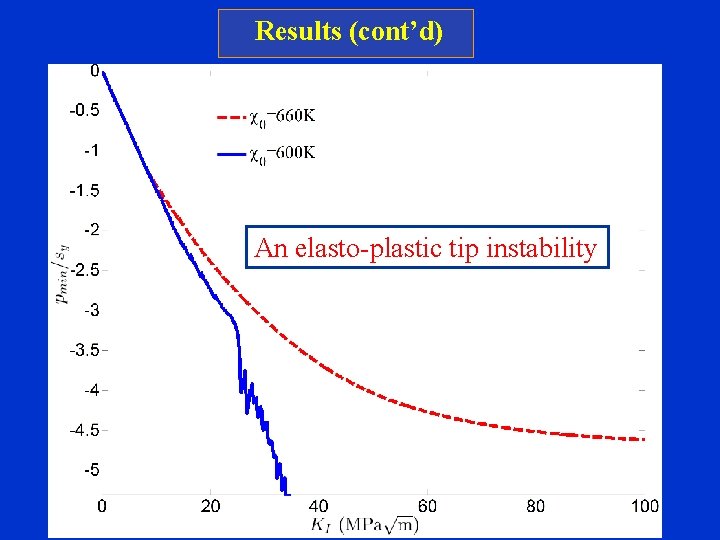
Results (cont’d) An elasto-plastic tip instability

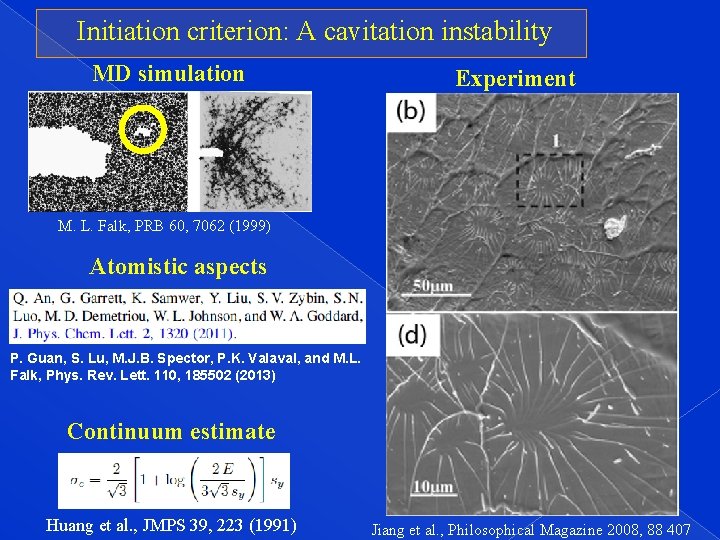
Initiation criterion: A cavitation instability MD simulation Experiment M. L. Falk, PRB 60, 7062 (1999) Atomistic aspects P. Guan, S. Lu, M. J. B. Spector, P. K. Valaval, and M. L. Falk, Phys. Rev. Lett. 110, 185502 (2013) Continuum estimate Huang et al. , JMPS 39, 223 (1991) Jiang et al. , Philosophical Magazine 2008, 88 407

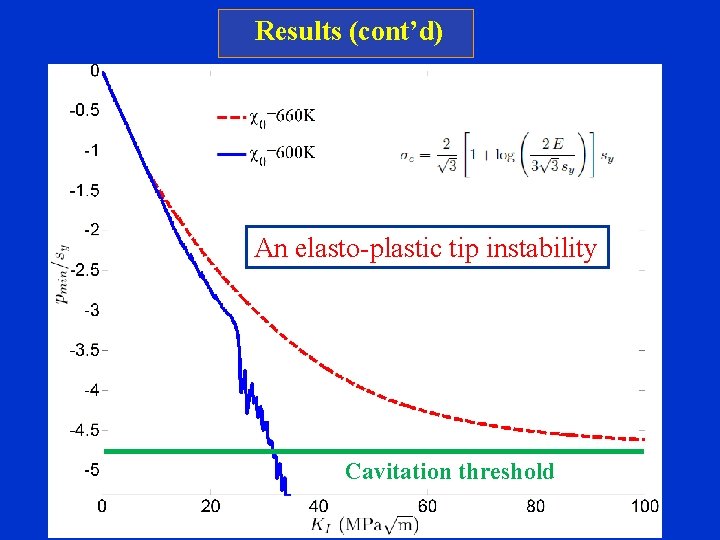
Results (cont’d) An elasto-plastic tip instability Cavitation threshold

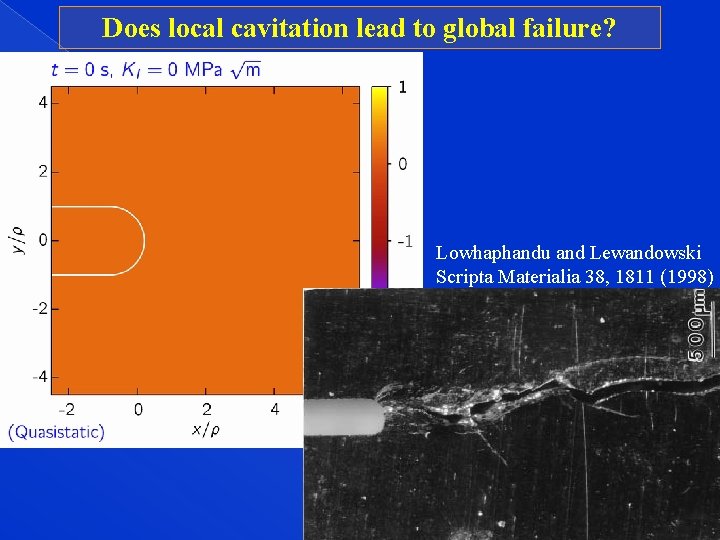
Does local cavitation lead to global failure? Lowhaphandu and Lewandowski Scripta Materialia 38, 1811 (1998)

Fracture energy [KJ/m 2] Final comments Poisson’s ratio

Summary The effective temperature concept is important for describing the mechanical properties of glassy/disordered materials. We demonstrated the existence of a new elasto-plastic crack tip instability as a function the degree of structural relaxation Our results offer a possible explanation for the observed annealing-induced ductile-to-brittle transition and may open the way for a better understanding of the toughness of metallic glasses Chris H. Rycroft and Eran Bouchbinder, Phys. Rev. Lett. 109, 194301 (2012)

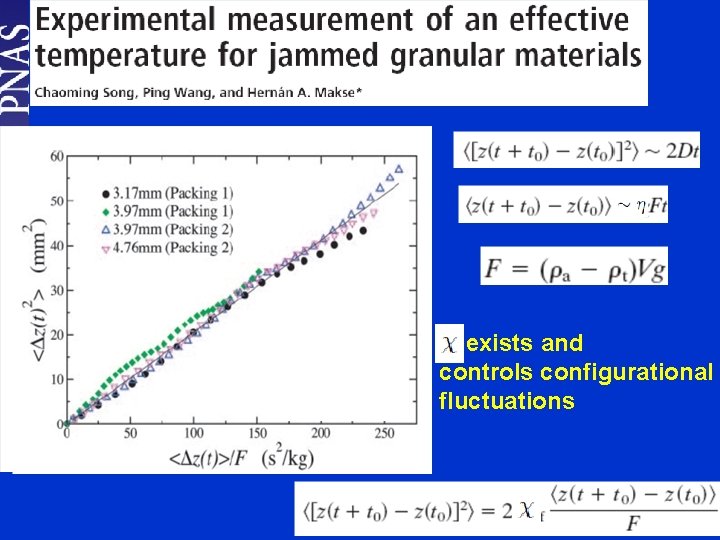
exists and controls configurational fluctuations