Fracture of Solids Liberty ship SS Schenectady was

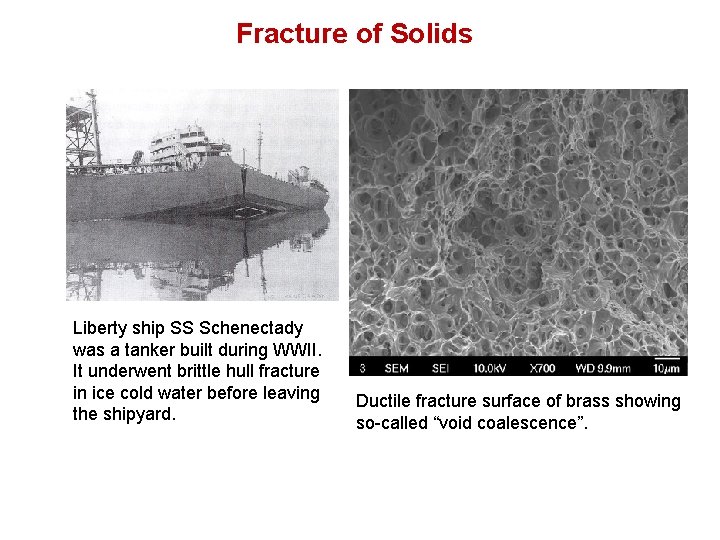
Fracture of Solids Liberty ship SS Schenectady was a tanker built during WWII. It underwent brittle hull fracture in ice cold water before leaving the shipyard. Tensile fracture of a brass rod showing characteristic cup-cone. Ductile fracture surface of brass showing so-called “void coalescence”.

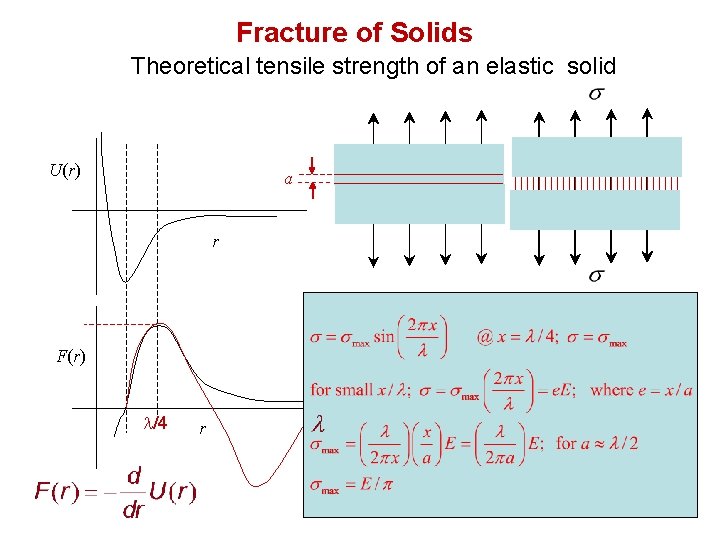
Fracture of Solids Theoretical tensile strength of an elastic solid U(r) a r F(r) l/4 r

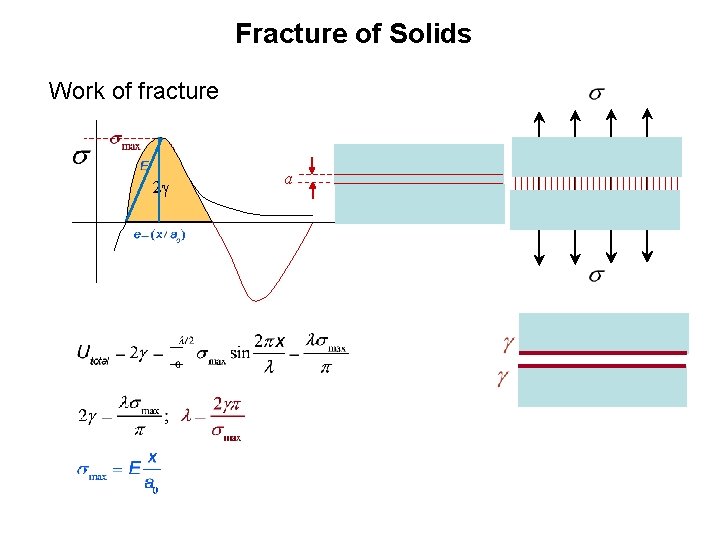
Fracture of Solids Work of fracture 2 g a

Theoretical strength of a defect-free solid Work of fracture for a defect-free solid

Theoretical strength of a defect-free solid Work of fracture for a defect-free solid Take E = 10 G Pa = 1010 Pa, g = 2 J m-2, ao = 3 x 10 -10 m.

Stress Concentrations Airy stress function a

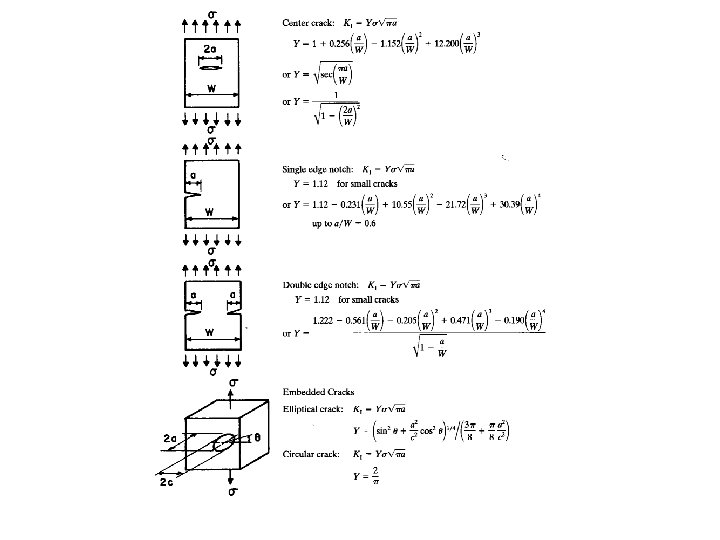
Stress Concentrations Elliptical flaw Def: Stress Concentration factor, Kt 2 b 2 a For the circular flaw The radius of curvature at a is, so, for

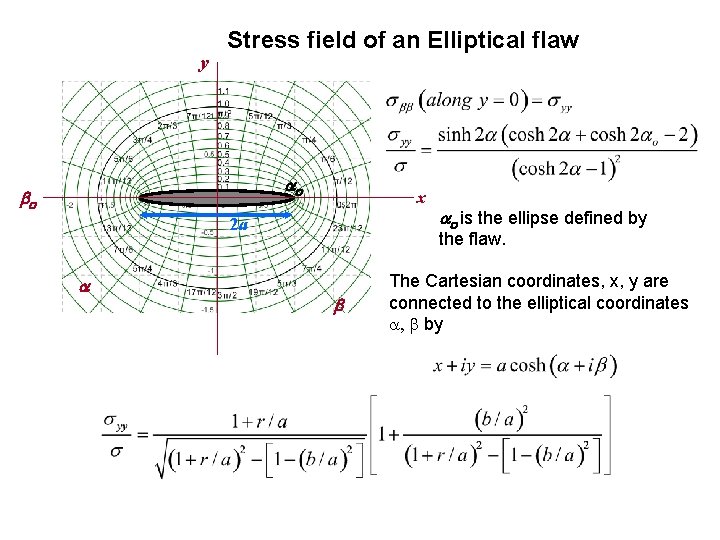
y Stress field of an Elliptical flaw ao bo x 2 a a ao is the ellipse defined by the flaw. b The Cartesian coordinates, x, y are connected to the elliptical coordinates a, b by

Stress field of an Elliptical flaw r is the distance along y = 0. The relative values of r/a and b/a compared to 1 determine the behavior of and define regions of interest. In the region r/a < 1 the leading term (dominant) including the bluntness contribution of b/a is, r<a As b/a 0 (a sharp “crack”) the stress field decays as (a/r)1/2. r < a: near field In the region, r/a >1 and the stress field scales as (a/r)2 r > a: far field

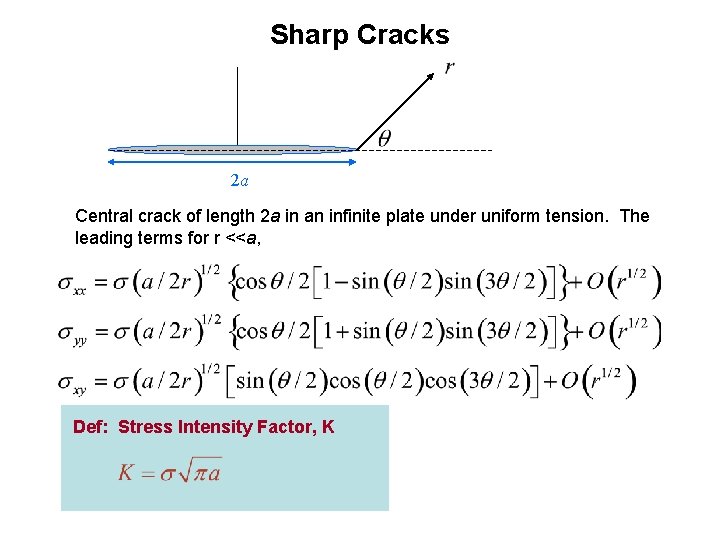
Sharp Cracks 2 a Central crack of length 2 a in an infinite plate under uniform tension. The leading terms for r <<a, Def: Stress Intensity Factor, K

Sharp Cracks These equations are often written in short-hand as: The stress intensity factor, K, defines the strength of the crack in much the same way as the Burgers vector defines the strength of a dislocation.

Crack Loading Modes Mode I: Opening Mode II: In-plane shear Mode III: Out-of plane or longitudinal shear

Units of K Y = numerical factor depending on geometry and loading MPa

Sharp Cracks Mode I stress field Cartesian coordinates Cylindrical polar coordinates

Sharp Cracks Mode II stress field Cartesian coordinates Mode III stress field Cartesian coordinates

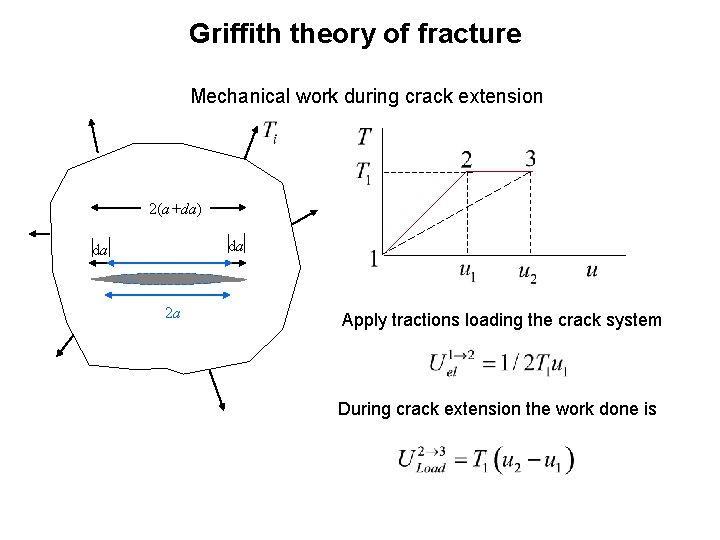
Griffith theory of fracture Mechanical work during crack extension 2(a+da) da da 2 a Apply tractions loading the crack system During crack extension the work done is

Griffith theory of fracture Mechanical work during crack extension The elastic energy at location 3 is just The change in elastic energy is just Then

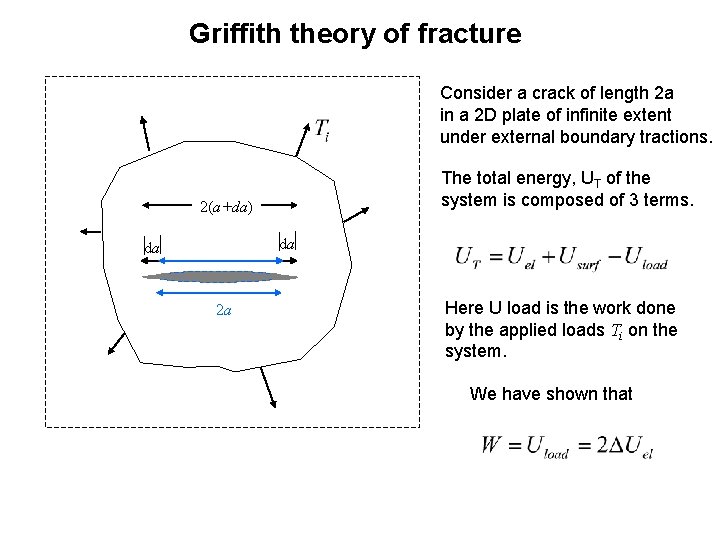
Griffith theory of fracture Consider a crack of length 2 a in a 2 D plate of infinite extent under external boundary tractions. The total energy, UT of the system is composed of 3 terms. 2(a+da) da da 2 a Here U load is the work done by the applied loads Ti on the system. We have shown that

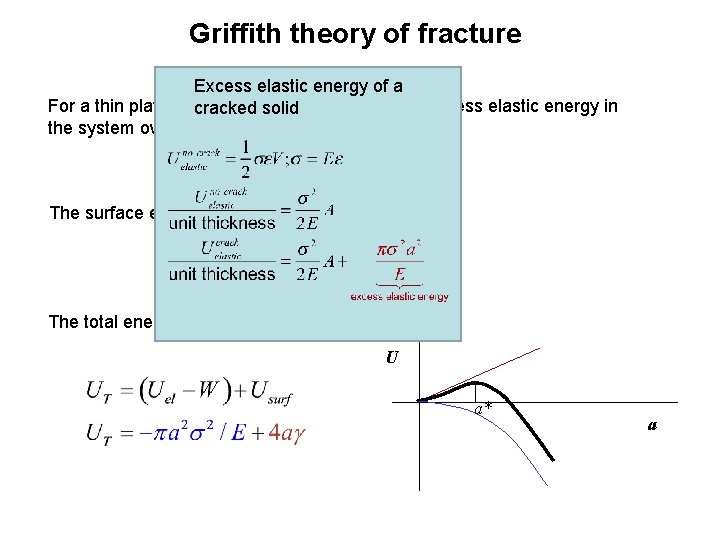
Griffith theory of fracture Excess elastic energy of a For a thin plate of unit thickness cracked solid under load the excess elastic energy in the system owing to the presence of the crack is, The surface energy of the crack system is The total energy may now be written as U a* a

Griffith theory of fracture We can find the position of the energy for fracture, corresponding to the maximum in UT, For the case of plane strain

Griffith theory of fracture Def: Crack extension force G is the (negative) change of potential energy per unit crack extension per unit width. Energy/area = Force/length

Griffith theory of fracture Plane Strain We can rearrange this to read What is a “typical value” of K at which fracture of a brittle solid is predicted E ~ 1011 Pa, g ~ 1 Jm-2 Many materials exhibit critical K values 10 -100 times larger then this. Why?

Many materials exhibit critical K values 10 -100 times larger then this. Why? This is the order of magnitude value we expect for the critical stress intensity for fracture of a metal based on the Griffith theory. Is there a mathematical limit to the value of r in the equation for the cracktip stress field? Is there a physical limit to the value of r in the equation for the crack-tip stress field?

Many materials exhibit critical K values 10 -100 times larger then this. Why? This is the order of magnitude value we expect for the critical stress intensity for fracture of a metal based on the Griffith theory. Is there a mathematical limit to the value of r in the equation for the cracktip stress field? Is there a physical limit to the value of r in the equation for the crack-tip stress field? YES! an interatomic spacing

Crack tip plasticity Based on the crack tip stress field, will there (always? ) be a region near the crack tip where the yield stress of the metal is exceeded. Let’s ignore the term, and set equal to the yield strength. Estimate of the plastic zone size A typical yield strength of a high strength steel is 300 MPa.

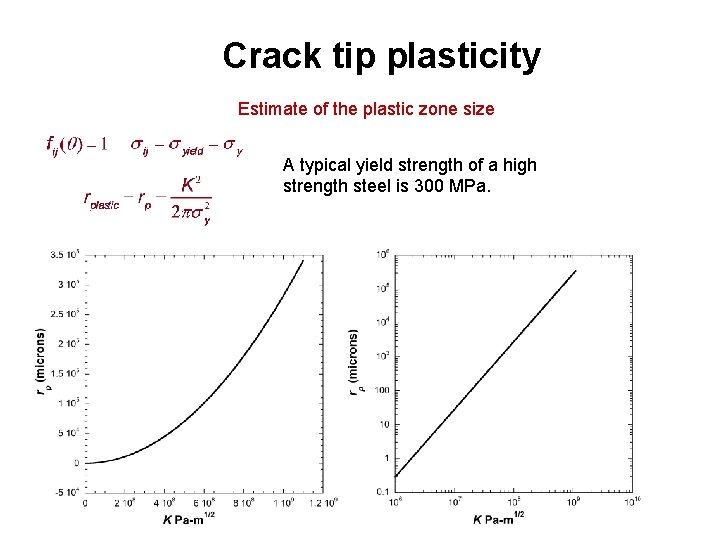
Crack tip plasticity Estimate of the plastic zone size A typical yield strength of a high strength steel is 300 MPa.

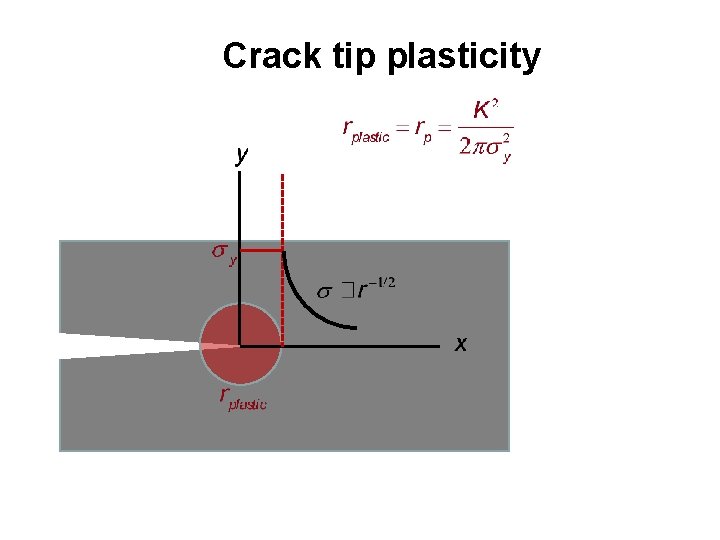
Crack tip plasticity

Crack tip plasticity Estimate of the plastic zone size The smallest possible size of the plastic zone corresponds to about a lattice spacing. Let’s examine what the value of would have to be, to correspond to a lattice spacing at the typical value of the critical Griffith value of the stress intensity factor, K = 0. 45 MPa. How does this compare to theoretical fracture stress of a solid?

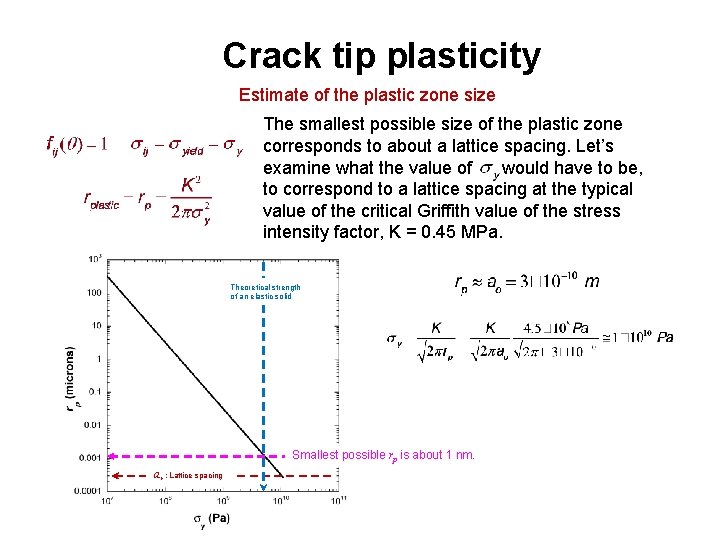
Crack tip plasticity Estimate of the plastic zone size The smallest possible size of the plastic zone corresponds to about a lattice spacing. Let’s examine what the value of would have to be, to correspond to a lattice spacing at the typical value of the critical Griffith value of the stress intensity factor, K = 0. 45 MPa. Theoretical strength of an elastic solid Smallest possible rp is about 1 nm. ao : Lattice spacing

Crack tip plasticity on a microscopic scale Dislocations define the plastic zone size Crack tip dislocation interactions and dislocation– dislocation interactions via the Peach-Kohler equation.

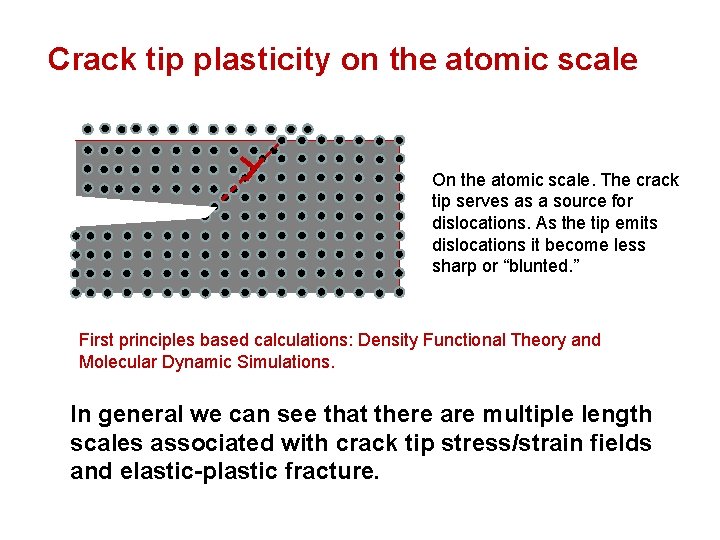
Crack tip plasticity on the atomic scale On the atomic scale. The crack tip serves as a source for dislocations. As the tip emits dislocations it become less sharp or “blunted. ” First principles based calculations: Density Functional Theory and Molecular Dynamic Simulations. In general we can see that there are multiple length scales associated with crack tip stress/strain fields and elastic-plastic fracture.