Fractions Day 4 Fractions n Numbers such as

Fractions Day 4

Fractions n Numbers such as ½ and -¾ are called fractions. n The number above the fraction line is called the numerator. n The number below the fraction line is called the denominator.

Reducing Fractions n When both the numerator and denominator have a common divisor, we can reduce the fraction to its lowest terms. n A fraction is said to be in its lowest terms (or reduced) when the numerator and denominator are relatively prime (have no common divisors other than 1).

n To reduce a fraction to its lowest terms, divide both the numerator and the denominator by the GCD. n The fraction 6/10 is reduced to its lowest terms as follows.

You Try… n Reduce to its lowest terms

Mixed Numbers and Improper Fractions n The number 2¾ is an example of a mixed number. It is called a mixed number because it is made up of an integer and a fraction. n 2¾ means 2 + ¾ n An improper fraction is a fraction whose numerator is greater than its denominator.

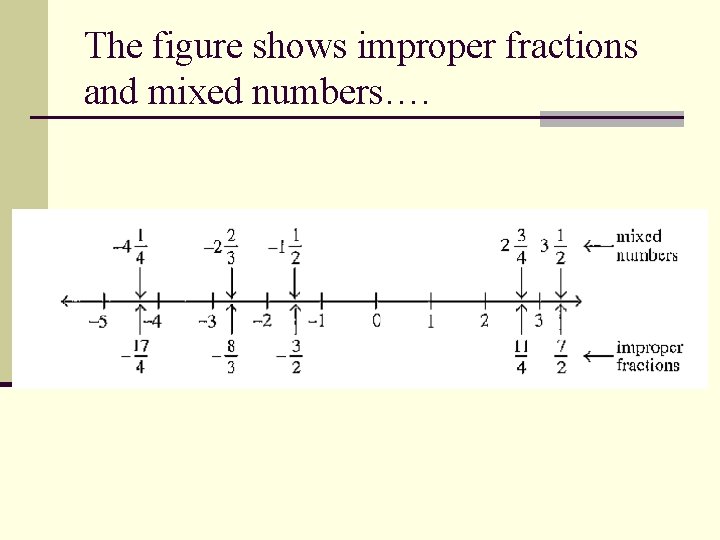
The figure shows improper fractions and mixed numbers….

How do you convert mixed numbers to improper fractions?

Example: Convert to Improper Fractions.

How do you convert improper fractions to mixed numbers?

Example: Convert number. to a mixed

Example: Convert number. to a mixed

Multiplication of Fractions n Multiply the numerators and multiply the denominators together then reduce if necessary.

Examples

Reciprocal n The reciprocal of any number is 1 divided by that number. n The product of a number and its reciprocal must equal 1.

Division of Fractions n To find the quotient of two fractions, multiply the first fraction by the reciprocal of the second fraction.

Addition and Subtraction of Fractions n Before we can add or subtract fractions, the fractions must have a lowest common denominator.

Example: Evaluate

Adding or Subtracting Fractions with Unlike Denominators n Use prime factorization to find the LCD for the denominator. n Example: LCD

Addition Example Now Reduce!