Fractions A Vertical Look 3 8 What fraction

Fractions A Vertical Look 3 -8

What fraction of the design is colored? Which has the most color?

We will: • Examine the Number and Operations Fractions domain in the TN Math Standards and analyze the content progressions. • Apply content progressions to instructional tasks. • Summarize new learning so we can plan effective lessons and create aligned tasks and assessments.

How? • Read, build, draw • Talk • Write and Record

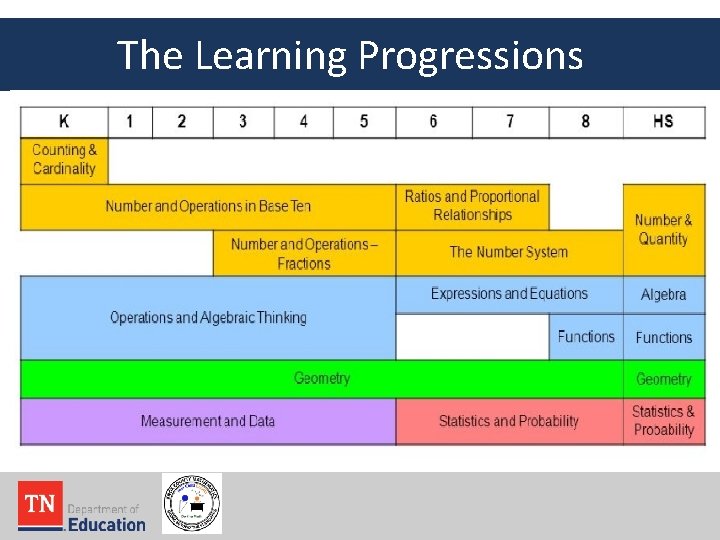
The Learning Progressions

Instructional Shifts • Focus – The standards are focused on fewer topics so that students can dig deeper within the mathematics. • Coherence – Topics within a grade are connected to support focus. Additionally, standards are linked across grades to ensure vertical coherence. • Rigor – The standards set expectations for a balanced approach to pursuing conceptual understanding, procedural fluency, application, and modeling.

Expectation Three: Rigor • Procedural Skill and Fluency: The standards call for speed and accuracy in calculation. • Conceptual Understanding: The standards call for conceptual understanding of key concepts, such as place value and ratios. • Modeling/Application: The standards call for students to use math in situations that require mathematical knowledge.

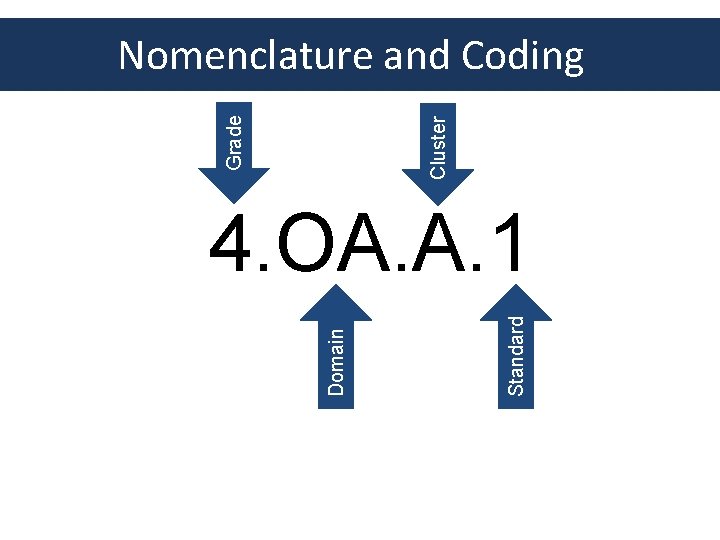
Cluster Grade Nomenclature and Coding Standard Domain 4. OA. A. 1

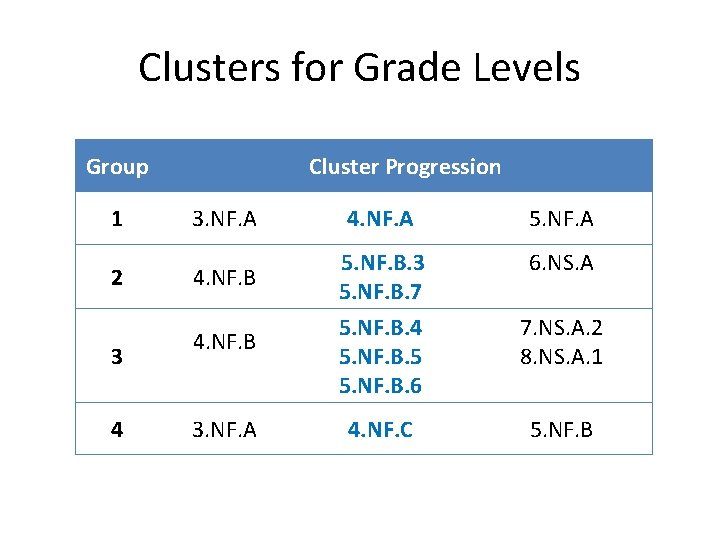
Clusters for Grade Levels Group 1 2 3 4 Cluster Progression 3. NF. A 4. NF. B 3. NF. A 4. NF. A 5. NF. B. 3 5. NF. B. 7 5. NF. B. 4 5. NF. B. 5 5. NF. B. 6 6. NS. A 4. NF. C 7. NS. A. 2 8. NS. A. 1 5. NF. B

Step 1: Focus Thinking Around One Big Idea • Review the assigned clusters. • Discuss the big idea that each cluster is asking the students to know and be able to do.

Step 2: Collaborate & Discuss Changes • How is the cluster different from the previous grade level? • Are there new concepts introduced or added? • Are any concepts dropped? • How does the demand of the cluster change? • Does an idea or skill get more complex? How? – (Analyze the verbs)

Step 3: Consider Rigor when Planning Instruction • Is this a new concept that has never been taught? • What content knowledge should be developed or shared? • What resources or support might we need to teach this concept? • What types of assessment might we need to measure this learning?

Expectation Three: Rigor • Procedural Skill and Fluency: The standards call for speed and accuracy in calculation. • Conceptual Understanding: The standards call for conceptual understanding of key concepts, such as place value and ratios. • Modeling/Application: The standards call for students to use math in situations that require mathematical knowledge.

Summarize Instructional Shifts • Focus: what is the focus of each grade level • Coherence: what changes from grade to grade • Rigor: Where do you see the 3 aspects of rigor

Break

Graham Fletcher Video Fractions Progression • Pull it all together • Stop and Chat

Norms • Provide explanations and justifications with all answers • Make sense of each others’ solutions • Say when you don’t understand or don’t agree

Developing Understanding of Fractions as Numbers Justify each students thinking. Michael says the image represents 2. Sophie says the image represents 2/3. Kate says the image represents 2/6.

Understanding Equivalence Compare 2/3 and 8/10. Show you arrived at this conclusion.

Add and Subtract Make sense of the problem: Two fifths of the cross-country team arrived at the weight room at 7 am. Ten minutes later, 3/10 of them showed up. The rest of the team stayed home.

3 Act Task The Apple

Planning • Reflect on this session: – What did you come to understand? – What did you discuss? – What groupings/ format did you use to discuss? – What scaffolds were provided? When were they provided? – How did you record and share your thinking?