Fractals in Nature And what you have to

Fractals in Nature And what you have to know about them

What are Fractals? v A curve or geometric figure, each part of which has the same statistical character as the whole. Self-similar subsets of Euclidean space whose fractal dimension strictly exceeds its topological dimension. Fractals appear the same at different levels, as illustrated in successive magnifications of the Mandelbrot set; because of this, fractals are encountered ubiquitously in nature.

Where we can find Fractals? • We can find fractals all over the natural world, from tiny patterns like seashells up to the giant spirals of the galaxies. Even the footprints of your fingers is considered a fractal!

History of Fractals • The history of fractals dates back to 1975, when Fractals were discovered by Benoît Mandelbrot. He explained them as being geometric shapes that when divided into parts, each part would be a smaller replica of the whole shape. He came up with the term "Fractal" as the new scientific term for this mathematical expression. The word is actually an adaptation of the Latin word fractus. The Latin word fractus means "broken" or "fractured".

Mandelbrot Fractals • Mandelbrot fractals were discovered first, so they were the most well-known fractals. Benoît is now known as the "father" of fractal geometry, so they remain the most popular today. Their shape is similar to a turtle with many legs and very large head. There are programs available that allow you to layer several "brots" as they are called normally as a single image. This creates a great spectacle for the eyes as fractals converge together to create amazing designs.

Julia Fractals • Julia Fractals were discovered by Gaston Julia and praised by Mandlebrot after his discovery. Julia's principle's were close to the findings of another great mathematician of that era, Pierre Fatou. They spent a great deal of time working together to come up with what is known as the, Generalized Fatou Julia theorem.

Newton Fractals were derived from "Isaac Newton's method". They create a totally different look than most fractal sets. Newton fractals are just proof that Isaac Newton was a great mathematician for his time. They have a very crisp and clean look to their geometric shape.

Fractals in Nature • A fractal is a pattern that the laws of nature repeat at different scales. Examples are everywhere in the forest.

Fractals in Math • Fractal, in mathematics, any of a class of complex geometric shapes that commonly have “fractional dimension, ” a concept first introduced by the mathematician Felix Hausdorff in 1918. Fractals are distinct from the simple figures of classical, or Euclidean, geometry—the square, the circle, the sphere, and so forth.

Examples of Fractals in Nature

Trees are natural fractals, patterns that repeat smaller and : smaller copies of themselves. Each tree branch, from the trunk to the tips, is a copy of the one that came before it.

Lightning bolts: • Another naturally occurring fractal pattern is a lightning bolt. As Benoit Mandelbrot noted in the opening quotation, lightning does not travel in straight lines. Rather, it follows a chaotic, jagged path, formed as the huge charge separation built up in the sky suddenly breaks down.

• A tiny animal, but with a lot of fractals. Their bulbous toes are covered in hundreds of tiny microscopic hairs called setae. Gecko’s Foot:

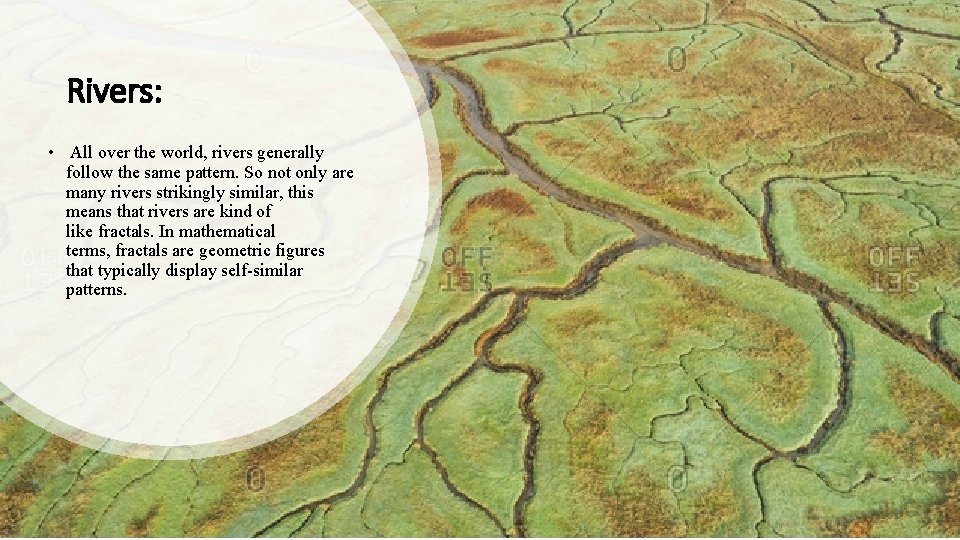
Rivers: • All over the world, rivers generally follow the same pattern. So not only are many rivers strikingly similar, this means that rivers are kind of like fractals. In mathematical terms, fractals are geometric figures that typically display self-similar patterns.

Mountains: • Mountains are the result of tectonic forces pushing the crust upward and erosion tearing some of that crust down. The resulting pattern is a fractal.

Romanesco Broccoli: • This variant form of cauliflower is the ultimate fractal vegetable. Its pattern is a natural representation of the Fibonacci or golden spiral, a logarithmic spiral where every quarter turn is farther from the origin by a factor of phi, the golden ratio.

Peacock Feathers: Peacocks attract mates with the repeating patterns in their plumage.

Sea Shells: Many of these shells have spectacularly complex shapes— logarithmic spirals bedecked with fractal spines or other ornaments, all executed with near-perfect mathematical regularity.

Snowflakes: Crystallizing water forms repeating patterns in snowflakes and on frosty surfaces. No two snowflakes are ever the same.

DNA: • These two properties of DNA combined — electron conduction and selfsymmetry — are the reasons why DNA acts as a fractal antenna.

Conclusion • So we already talked about fractals in nature, but why did we choose these types of fractals? Fractals in nature are seen globally, even without you noticing it. Fractals in nature are the most extensive type of fractals, giving us infinite options and variations. There may be even more fractals in nature that we haven't even discover yet. Who knows; maybe you'll be the next person in discover them!

Thanks for Watching our Presentation • Brayan Gonzalez • Adrian • Carlos Jacome • Andy Fonseca • Thifanie Cordoba • Julian Ms. Zogovic 4/17/20