FPtreeFPGrowth FP TreeFP Growth Algorithm Use a compressed

FPtree/FPGrowth

FP Tree/FP Growth Algorithm • Use a compressed representation of the database using an FP tree • Then use a recursive divide and conquer approach to mine the frequent itemsets.

Building the FP Tree 1. Scan data to determine the support count of each item. Infrequent items are discarded, while the frequent items are sorted in decreasing support counts. 2. Make a second pass over the data to construct the FP tree. As the transactions are read, before being processed, their items are sorted according to the above frequency order.

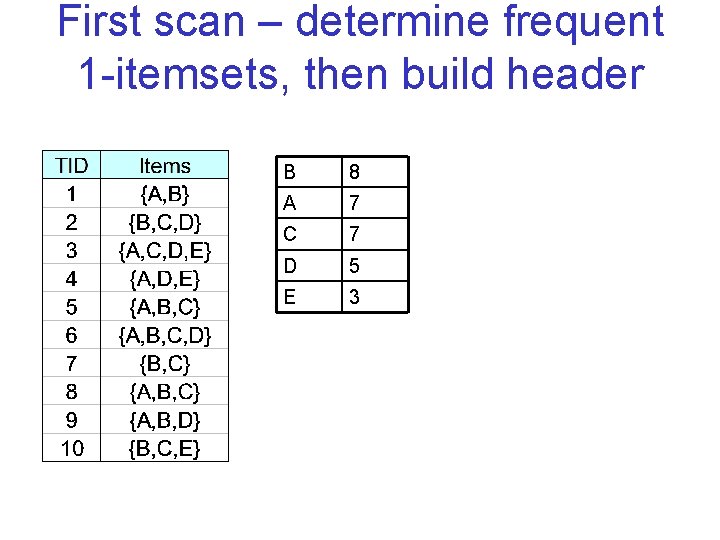
First scan – determine frequent 1 itemsets, then build header B 8 A 7 C 7 D 5 E 3

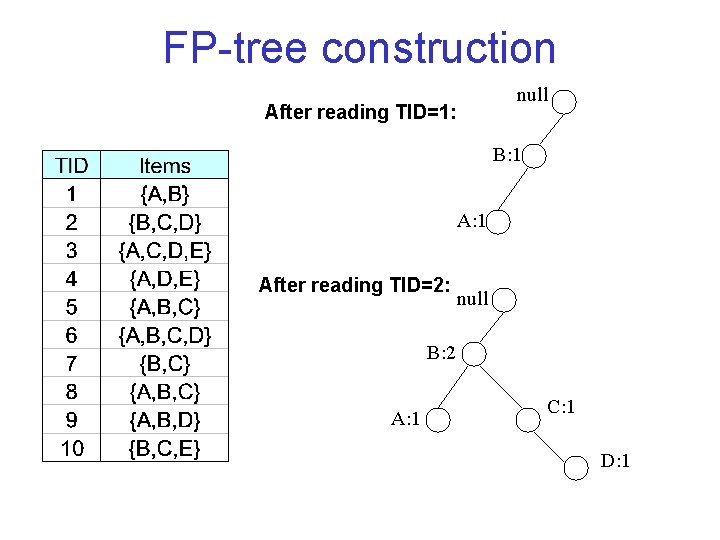
FP tree construction null After reading TID=1: B: 1 After reading TID=2: null B: 2 A: 1 C: 1 D: 1

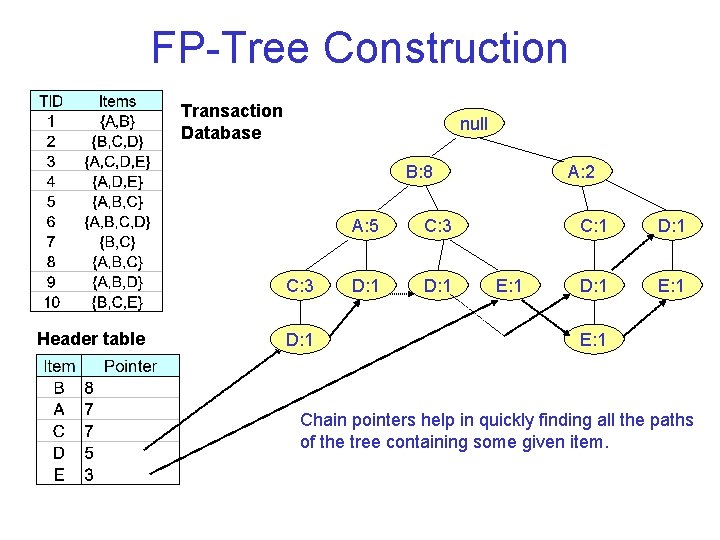
FP Tree Construction Transaction Database null B: 8 C: 3 Header table D: 1 A: 5 C: 3 D: 1 A: 2 E: 1 C: 1 D: 1 E: 1 Chain pointers help in quickly finding all the paths of the tree containing some given item.

FP Tree size • Size of FP tree is typically smaller than the size of the uncompressed data. – Because many transactions often share a few items in common. • Best casescenario: – All transactions have the same set of items, and the FP tree contains only a single branch of nodes. • Worst casescenario: – Every transaction has a unique set of items. • As none of the transactions have any items in common, the size of the FP tree is effectively the same as the size of the original data. • Size of FP tree also depends on how the items are ordered. – If the ordering scheme in the preceding example is reversed, i. e. , from lowest to highest support item, the resulting FP tree is denser.

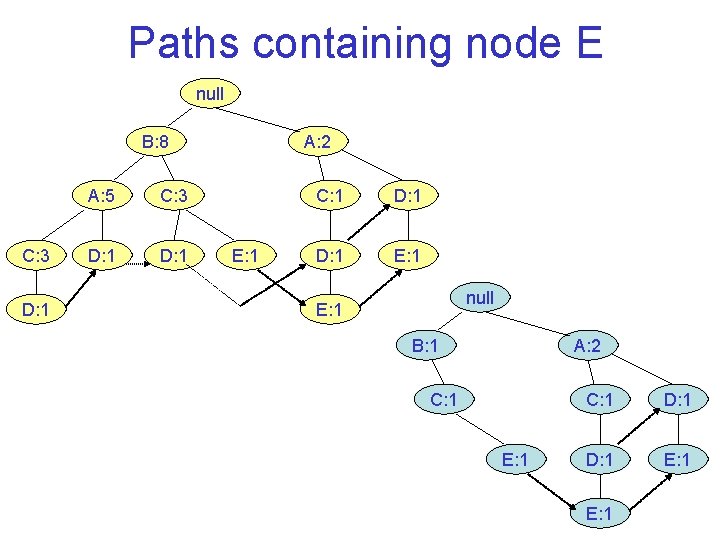
FP Growth • FP growth generates frequentitemsets by exploring the FP tree in a bottom upfashion. • It starts with the less frequent item, in this example, E. • Then, the algorithm looks for frequent itemsets ending in E first, followed by D, C, A, and finally, B. – We can derive the frequent itemsets ending with E, by examining only the paths containing node E. • These paths can be accessed rapidly using the pointers associated with node E.

Paths containing node E null B: 8 C: 3 D: 1 A: 5 C: 3 D: 1 A: 2 E: 1 C: 1 D: 1 E: 1 null E: 1 B: 1 A: 2 C: 1 E: 1 C: 1 D: 1 E: 1

Conditional FP Tree for E • FP Growth builds a conditional FP Tree for E, which is the tree of itemsets ending in E. • It is not the tree obtained in the previous slide as result of deleting nodes from the original tree. Why? • Because the order of the items can change. – Now, C has a higher count than B.

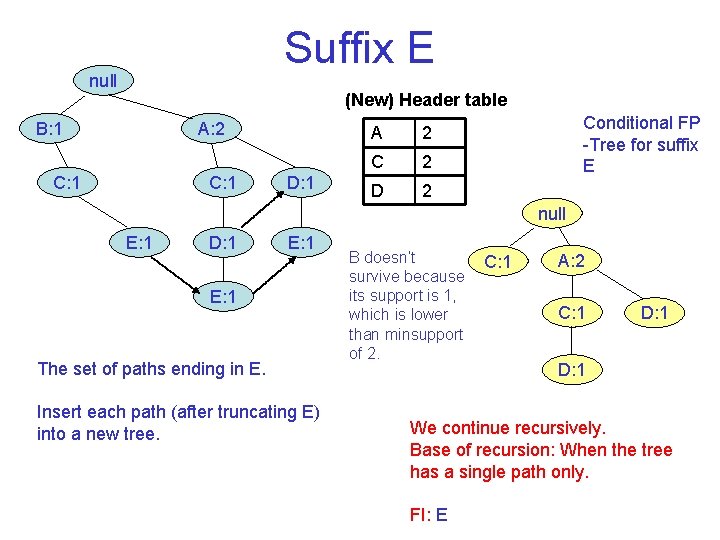
Suffix E null (New) Header table B: 1 A: 2 C: 1 D: 1 A 2 C 2 D 2 Conditional FP Tree for suffix E null E: 1 D: 1 E: 1 The set of paths ending in E. Insert each path (after truncating E) into a new tree. B doesn’t survive because its support is 1, which is lower than minsupport of 2. C: 1 A: 2 C: 1 D: 1 We continue recursively. Base of recursion: When the tree has a single path only. FI: E

Steps of Building Conditional FP Trees 1. Find the paths containing on focus item. 2. Read the tree to determine the new counts of the items along those paths. Build a new header. 3. Read again the tree. Insert the paths in the conditional FP Tree according to the new order.

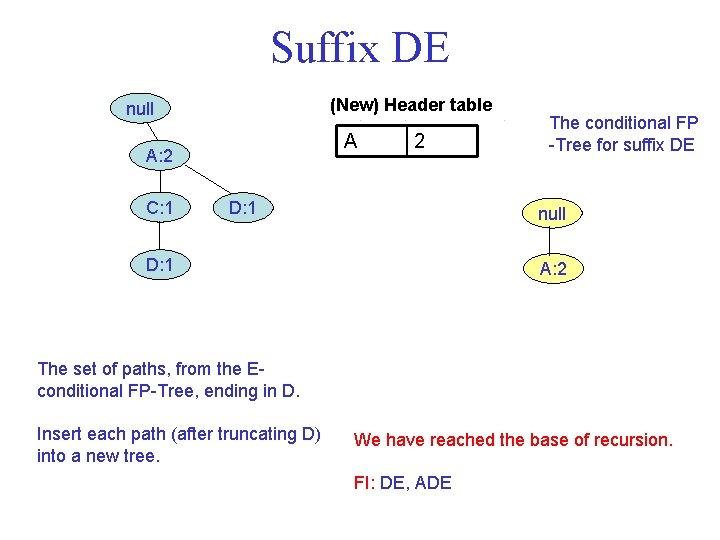
Suffix DE (New) Header table null A A: 2 C: 1 2 D: 1 The conditional FP Tree for suffix DE null D: 1 A: 2 The set of paths, from the E conditional FP Tree, ending in D. Insert each path (after truncating D) into a new tree. We have reached the base of recursion. FI: DE, ADE

Base of Recursion • We continue recursively on the conditional FP Tree. • Base case of recursion: when the tree is just a single path. – Then, we just produce all the subsets of the items on this path merged with the corresponding suffix.

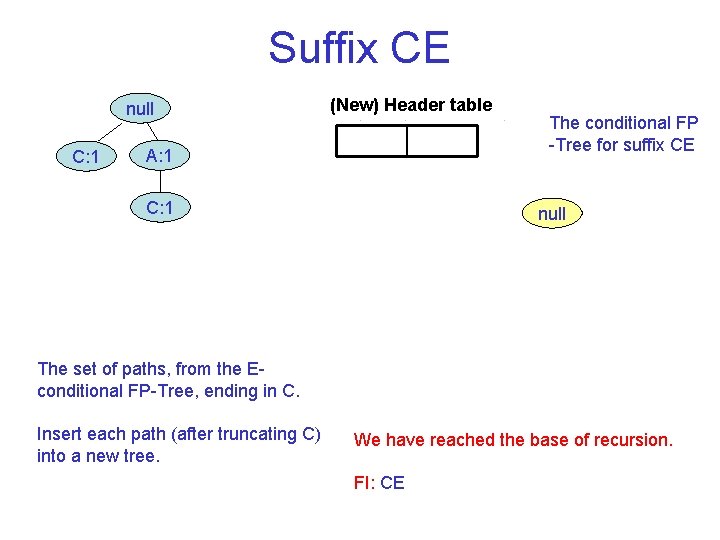
Suffix CE null C: 1 (New) Header table A: 1 C: 1 The conditional FP Tree for suffix CE null The set of paths, from the E conditional FP Tree, ending in C. Insert each path (after truncating C) into a new tree. We have reached the base of recursion. FI: CE

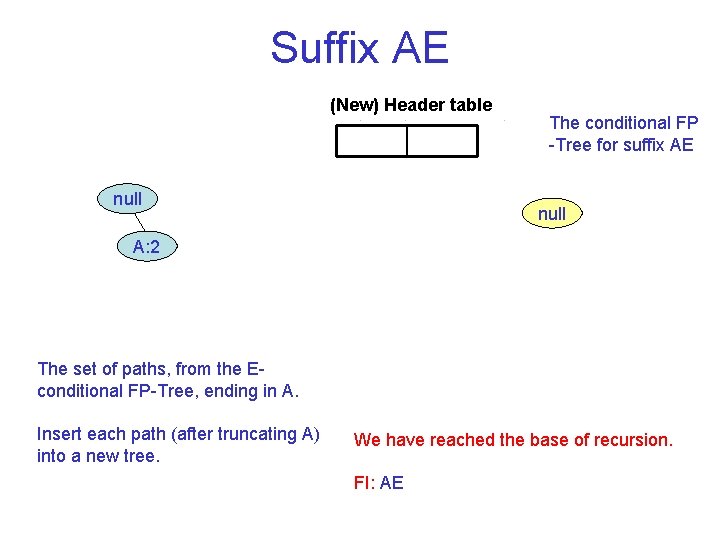
Suffix AE (New) Header table null The conditional FP Tree for suffix AE null A: 2 The set of paths, from the E conditional FP Tree, ending in A. Insert each path (after truncating A) into a new tree. We have reached the base of recursion. FI: AE

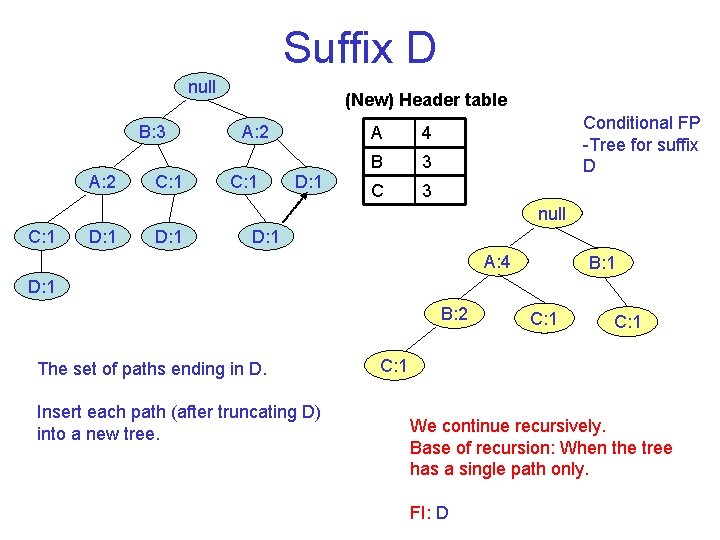
Suffix D null B: 3 A: 2 C: 1 (New) Header table A: 2 C: 1 D: 1 A 4 B 3 Conditional FP Tree for suffix D null C: 1 D: 1 A: 4 B: 1 D: 1 B: 2 The set of paths ending in D. Insert each path (after truncating D) into a new tree. C: 1 We continue recursively. Base of recursion: When the tree has a single path only. FI: D

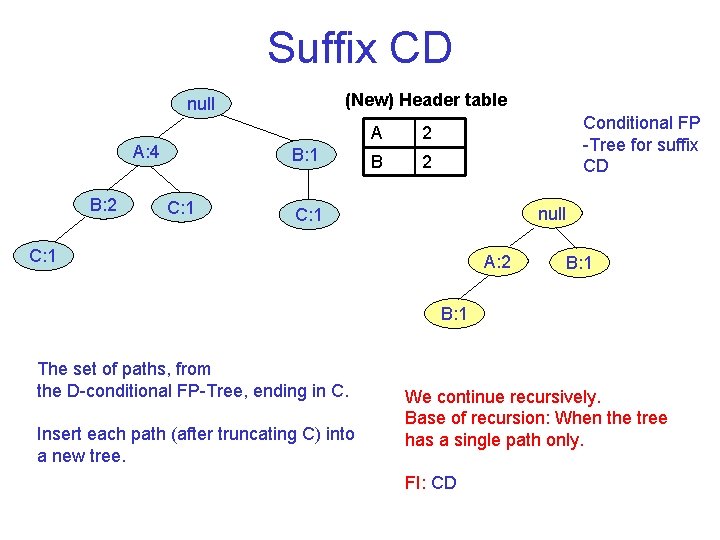
Suffix CD (New) Header table null A: 4 B: 2 B: 1 C: 1 A 2 B 2 Conditional FP Tree for suffix CD null C: 1 A: 2 B: 1 The set of paths, from the D conditional FP Tree, ending in C. Insert each path (after truncating C) into a new tree. We continue recursively. Base of recursion: When the tree has a single path only. FI: CD

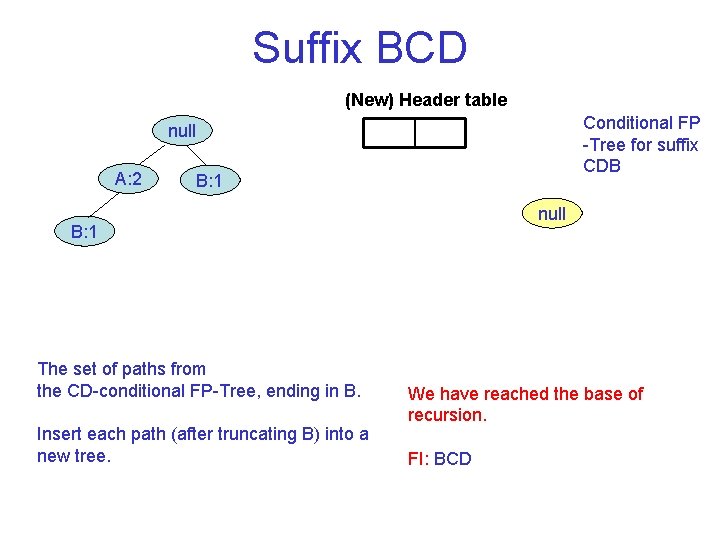
Suffix BCD (New) Header table Conditional FP Tree for suffix CDB null A: 2 B: 1 null B: 1 The set of paths from the CD conditional FP Tree, ending in B. Insert each path (after truncating B) into a new tree. We have reached the base of recursion. FI: BCD

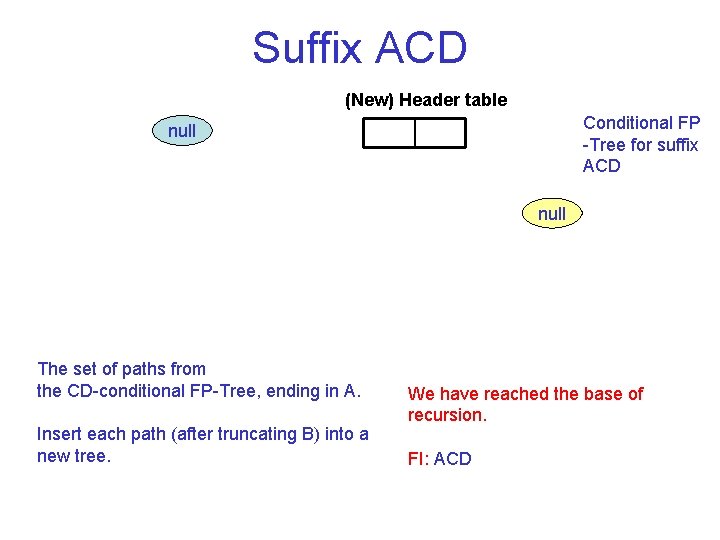
Suffix ACD (New) Header table Conditional FP Tree for suffix ACD null The set of paths from the CD conditional FP Tree, ending in A. Insert each path (after truncating B) into a new tree. We have reached the base of recursion. FI: ACD

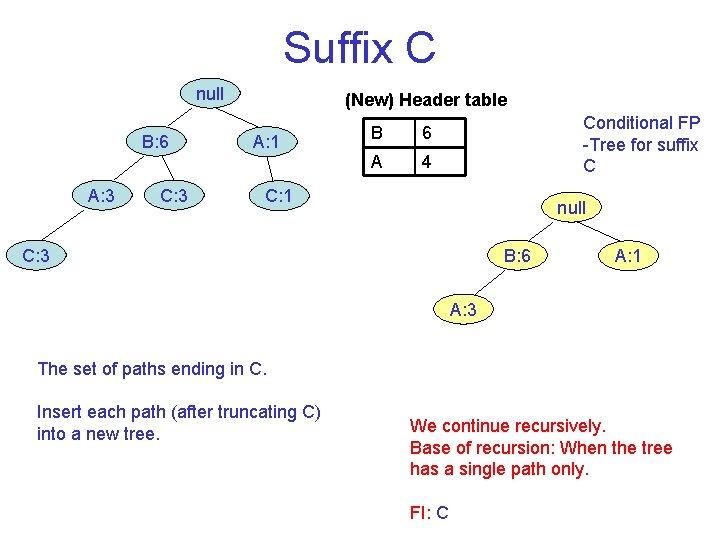
Suffix C null B: 6 A: 3 C: 3 (New) Header table A: 1 B 6 A 4 Conditional FP Tree for suffix C C: 1 null C: 3 B: 6 A: 1 A: 3 The set of paths ending in C. Insert each path (after truncating C) into a new tree. We continue recursively. Base of recursion: When the tree has a single path only. FI: C

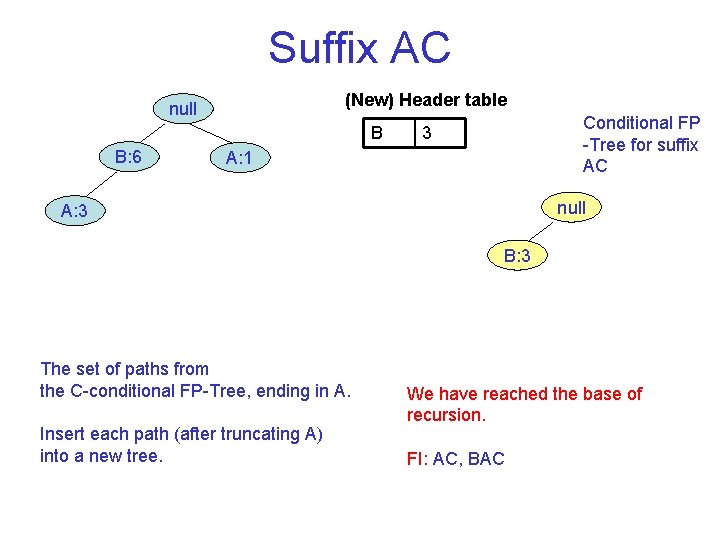
Suffix AC (New) Header table null B B: 6 Conditional FP Tree for suffix AC 3 A: 1 null A: 3 B: 3 The set of paths from the C conditional FP Tree, ending in A. Insert each path (after truncating A) into a new tree. We have reached the base of recursion. FI: AC, BAC

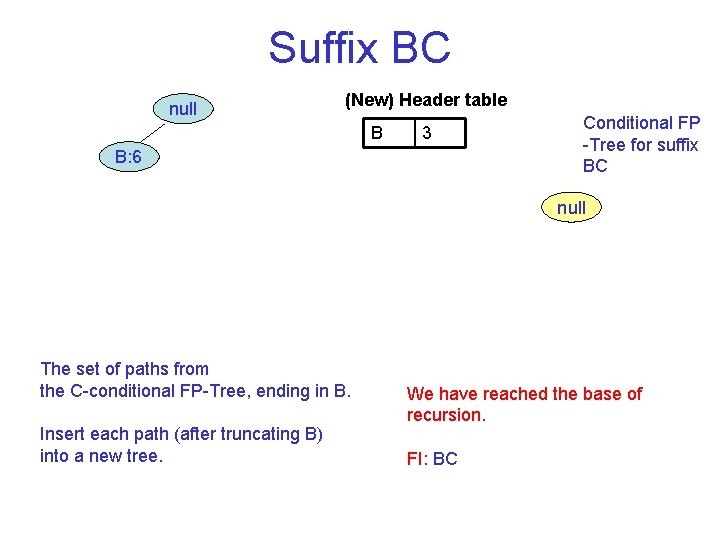
Suffix BC null (New) Header table B 3 B: 6 Conditional FP Tree for suffix BC null The set of paths from the C conditional FP Tree, ending in B. Insert each path (after truncating B) into a new tree. We have reached the base of recursion. FI: BC

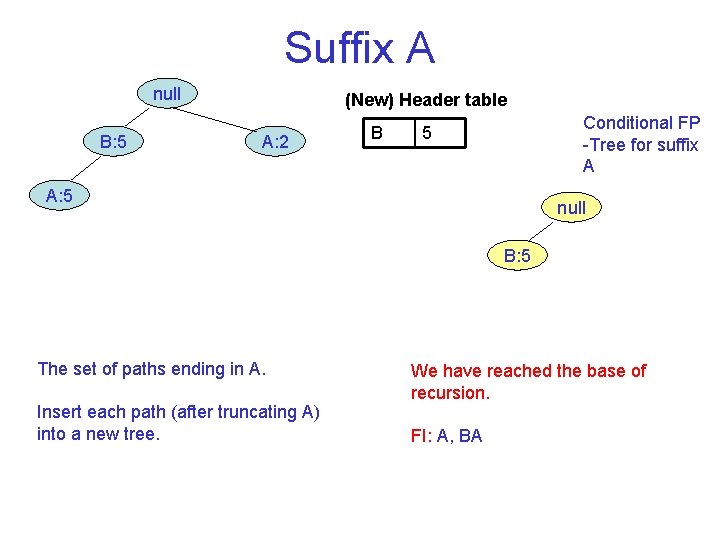
Suffix A null B: 5 (New) Header table A: 2 B Conditional FP Tree for suffix A 5 A: 5 null B: 5 The set of paths ending in A. Insert each path (after truncating A) into a new tree. We have reached the base of recursion. FI: A, BA

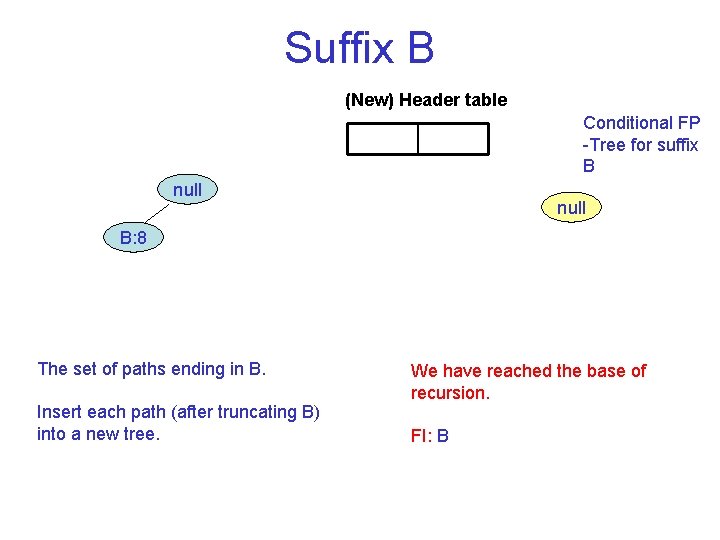
Suffix B (New) Header table Conditional FP Tree for suffix B null B: 8 The set of paths ending in B. Insert each path (after truncating B) into a new tree. We have reached the base of recursion. FI: B