Fourier Transforms and Their Use in Data Compression

Fourier Transforms and Their Use in Data Compression By Joseph Gehring

What is a Fourier Transform? • From Simple Wikipedia: – “A Fourier transform is a math function that makes a sometimes less useful function into another more useful function. ” – “A Fourier transform really just shows you what frequencies are in a signal. ”

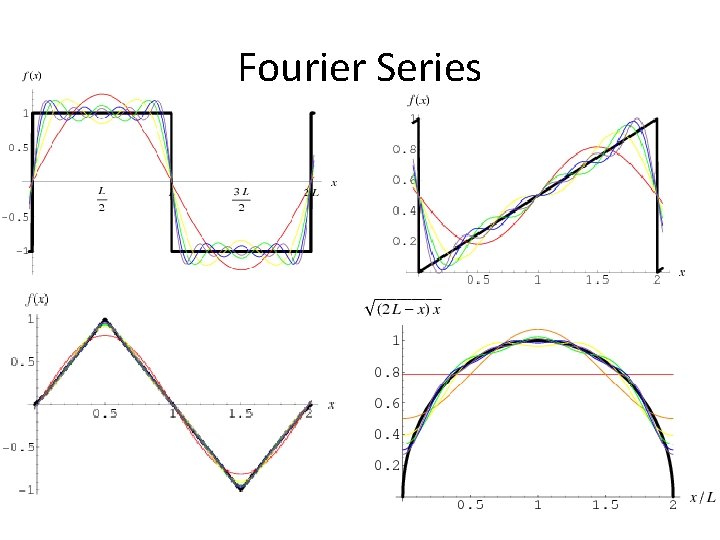
The Math • The Fourier Transform is a generalization of the Fourier Series • Any periodic function can be represented as an infinite sum of sines and cosines

Fourier Series

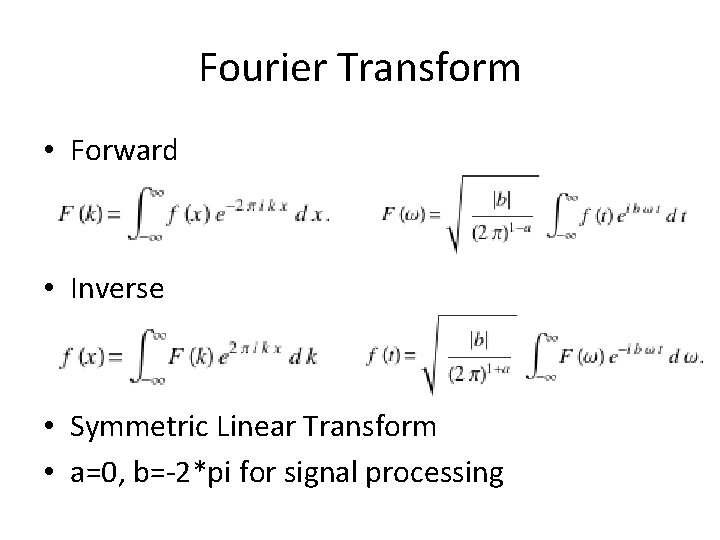
Fourier Transform • Forward • Inverse • Symmetric Linear Transform • a=0, b=-2*pi for signal processing

Fourier Transform • Every function f(x) has a forward and inverse Fourier Transform such that • Given: – Integral of f(x) exists – Discontinuous at a finite number of points – Function has a bounded variation

Discrete Fourier Transform • For given input data: – Reveals periodic elements – Shows the relative strength of those periodic elements • Input sequence of real numbers results in Fourier Transform output of complex numbers • Efficiently computed using Fast Fourier Transform

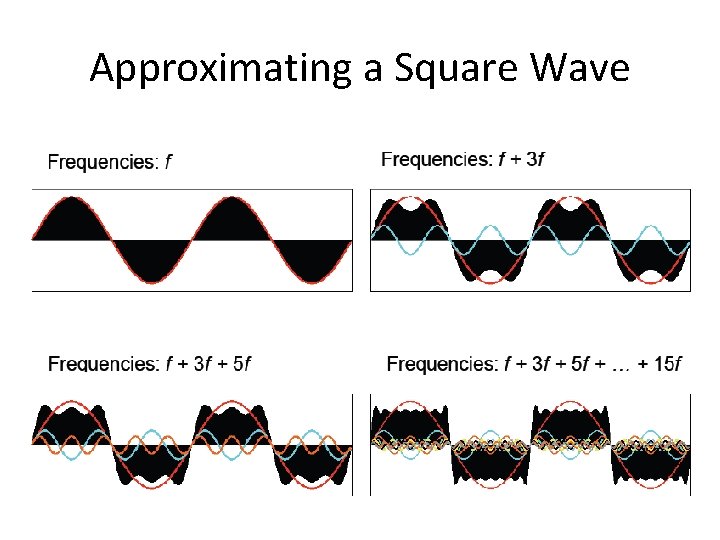
Some Clarification • Fourier Series uses an infinite sum of sines and cosines • Fourier Transform uses an integral over an infinite range to develop an approximation • Discrete Fourier Transform uses a finite sum of sines and cosines over a given range, based on sampling rates and sample length – In music, the sample rate is usually set to 44, 100 samples/second based on CD quality

Approximating a Square Wave

Fast Fourier Transform • Efficient algorithm reducing the number of computations required to determine the discrete Fourier Transform of a function from O(n^2) to O(n*log 2(n)) • Has been used in mp 3 and JPG compression • Ultimately, even the FFT could not compete with the Discrete Cosine Transform, which is the cosine portion of the Fourier Transform, and uses only real values

Compression • The compression ratio offered by use of the Fourier Transform is dependent on the quality required by the application • The higher quality the result needs to be, the lower the compression ratio will be • To create a more accurate output, more coefficients are needed and the data cannot be compressed as significantly

MP 3 • Input file is sampled, usually at 44. 1 k. Hz, and the file is split into chunks of 576 samples each (~. 013 seconds) • FFT or DCT is performed to convert time domain to frequency domain • Frequencies outside range of human hearing are removed • Coefficient data is stored in conjunction with a 32 -bit header containing sound quality (frame) • Multiple frames are combined to make a single mp 3 file • http: //www. indiana. edu/~acoustic/s 522/fourapdkp. html

JPG The original image is broken up into 64 pixel blocks, each 8 x 8 pixels. The DCT is taken of each 8 x 8 group using a set of 64 basis functions. Each numerical value in the group is replaced with a new, smaller number representing a coefficient for a basis function. Because these numbers are smaller, the number of bits required to represent them can be reduced. So, each value in the group is truncated to a lower number of bits. By storing this lower number of bits instead, the total amount of information is compressed.

JPG (cont’d) • In this image, we see how many coefficients are required to achieve an approximation of the original image. Using 15 coefficients for the Fourier Transform instead of 64 original values, a good approximation can be made of the initial image

JPG (Cont’d) • The last step of JPG compression involves the use of Huffman Encoding, which is a form of variable bit length encoding that uses fewer bits to represent values that occur more frequently than those that occur more rarely. • The 64 encoded values are then converted to a linear sequence of values rather than an array

In Conclusion • All these methods have undergone periodic updates depending on the complexity of input data and the computing power available to perform the tasks. • As storage space becomes cheaper, compression ratios can become less strict to create closer approximations to original information

This cat has some serious periodic components.

Works Cited “Fourier Transform. ” Simple Wikipedia. Web. 04 April 2011. http: //simple. wikipedia. org/wiki/Fourier_transform. Various Articles. Wolfram Math. World: The Web’s Most Extensive Mathematics Resource. Web. 03 April 2011. http: //mathworld. wolfram. com. “MP 3. ” Wikipedia, The Free Encyclopedia. Web. 04 April 2011. http: //en. wikipedia. org/wiki/MP 3. Smith, Steven W. “JPEG (Transform Compression). ” The Scientist and Engineer’s Guide to Digital Signal Processing. Web. 04 April 2011. http: //www. dspguide. com/ch 27/6. htm. Yoo, Yerin. “Tutorial on Fourier Theory. ” Department of Computer Science. University of Otago. Web. 05 April 2011. http: //www. cs. otago. ac. nz/cosc 453/student_tutorials/fourier_analysis. pdf Handley, Mark. “ 3: Fourier Transforms. ” Department of Computer Science. Columbia University. Web. 05 April 2011. http: //www. cs. columbia. edu/~hgs/teaching/ais/slides/03 -fourier. pdf Munroe, Randall. “Fourier. ” xkcd. Web. 05 April 2011. http: //xkcd. com/26.