Fourier Transform From Fourier Series to Fourier Transform

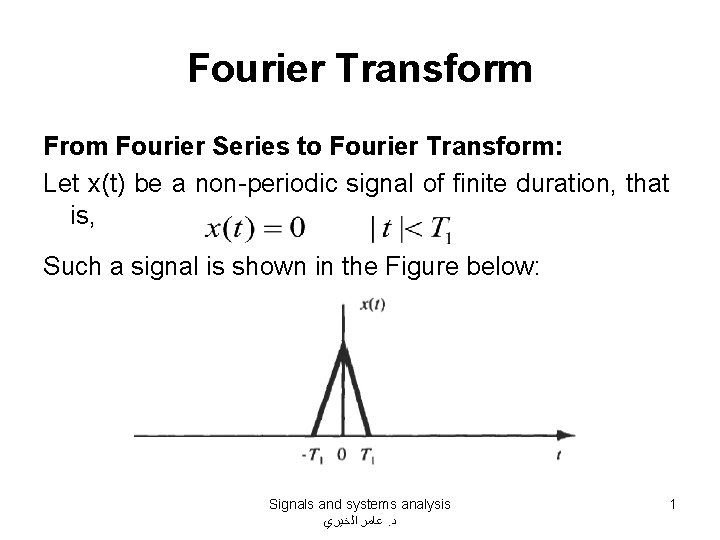
Fourier Transform From Fourier Series to Fourier Transform: Let x(t) be a non-periodic signal of finite duration, that is, Such a signal is shown in the Figure below: Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 1

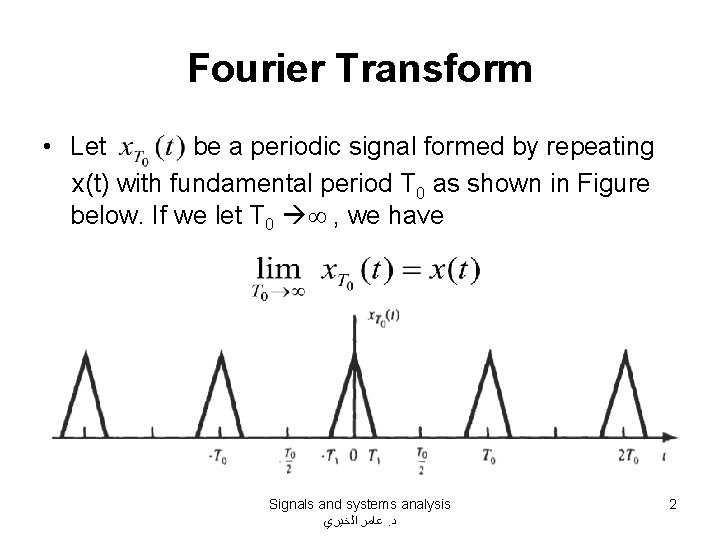
Fourier Transform • Let be a periodic signal formed by repeating x(t) with fundamental period T 0 as shown in Figure below. If we let T 0 , we have Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 2

Fourier Transform • The Fourier transform of x(t) is • The inverse Fourier transform of X(w) is Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 3

Fourier Transform Observations: • X(w) is in general a complex function. It is sometimes referred to as the spectrum of the signal x(t). • To denote that X(w) is the Fourier transform of x(t), the following notation is frequently employed • To denote that x(t) is the inverse Fourier transform of X(w) , the following notation is used • Sometimes the following notation is used as a shorthand for both relations: Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 4

Fourier Transform Convergence of FT: Just as in the case of periodic signals, the sufficient conditions for the convergence of X(w) are the following (referred to as the Dirichlet conditions): 1 - x(t) is absolutely integrable, that is, 2. x(t) has a finite number of maxima and minima within any finite interval. 3. x(t) has a finite number of discontinuities within any finite interval, and each of these discontinuities is finite. Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 5

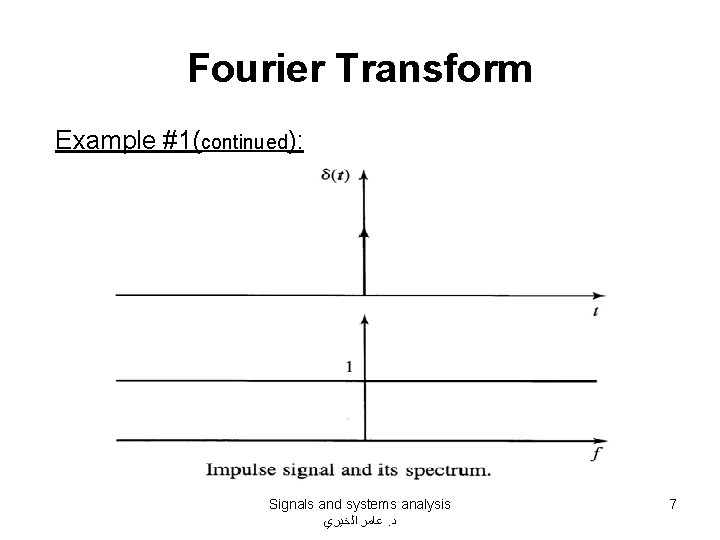
Fourier Transform Example #1: Find the FT of Dirac delta function. Therefore, Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 6

Fourier Transform Example #1(continued): Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 7

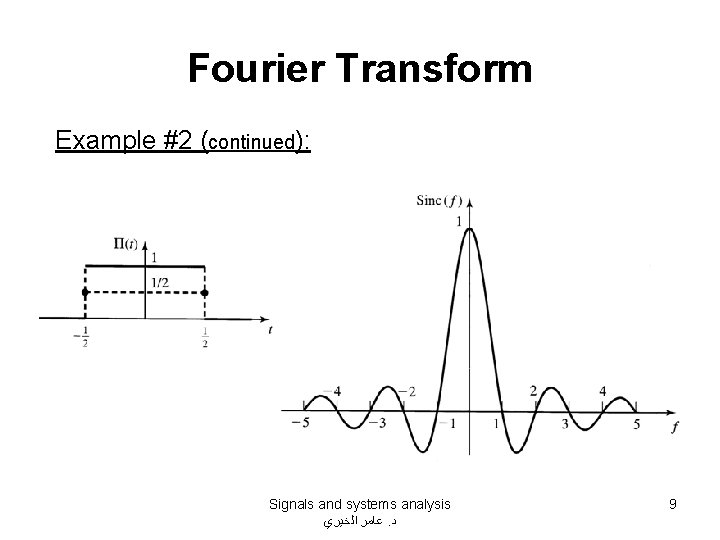
Fourier Transform Example #2: Determine the FT of the signal Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ . 8

Fourier Transform Example #2 (continued): Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 9

Properties of Fourier Transform 1 - Linearity: 2 - Time shifting: 3 - Frequency shifting: Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 10

Properties of Fourier Transform The multiplication of x(t) by a complex exponential signal is sometimes called complex modulation. This shows that complex modulation in the time domain corresponds to a shift of X(w) in the frequency domain. Note that the frequency-shifting Property is the dual of the time-shifting property. 4 - Time scaling: Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 11

Properties of Fourier Transform Where a is a real constant. indicates that scaling the time variable t by the factor a causes an inverse scaling of the frequency variable w by 1/a , as well as an amplitude scaling of X(w/a) by 1/|a|. Thus, the scaling property implies that time compression of a signal (a > 1) results in its spectral expansion and that time expansion of the signal (a < 1) results in its spectral compression. 5 - Time reversal: Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 12

Properties of Fourier Transform Where a is a real constant. indicates that scaling the time variable t by the factor a causes an inverse scaling of the frequency variable w by 1/a , as well as an amplitude scaling of X(w/a) by 1/|a|. Thus, the scaling property implies that time compression of a signal (a > 1) results in its spectral expansion and that time expansion of the signal (a < 1) results in its spectral compression. 5 - Time reversal: Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 13

Properties of Fourier Transform 6 - Duality: Consider the inverse FT defined as By replacing t by −t, we get Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 14

Properties of Fourier Transform This is a forward transform with 2πx(−t) being the FT of X(ω). To put it another way, we get 2πx(−t) by taking the FT of x(t) twice in succession, 2πx(−t) = FT(FT(x(t))). Let x(t) ⇐⇒ X(ω). If we replace the variable ω in the frequency domain function by ±t, then the corresponding frequency-domain function is obtained by replacing the variable t by ∓ω in the original timedomain function multiplied by 2π. For an even x(t), as X(ω) is also even, the sign change of either t or ω is not required. Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 15

Properties of Fourier Transform 7 - Time-differentiation: To show the benefit that we may get from this property in solving problems, let’s have the following example: Consider finding the FT of the triangular waveform x(t) = 0. 5(t + 2)u(t + 2) − tu(t) + 0. 5(t − 2)u(t − 2). This problem can be solved using the differentiation property. The FT of scaled and shifted impulse function can be found easily. Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 17

Properties of Fourier Transform The FT of scaled and shifted impulse function can be found easily. Therefore, the idea is to reduce the given function to a set of impulses by differentiating it successively. Then, the FT of the impulses can be related to the FT of the given function by the differentiation property. The first and second derivatives are: dx(t)/dt = 0. 5 u(t + 2) − u(t) + 0. 5 u(t − 2) and d 2 x(t)/dt 2 = 0. 5δ(t + 2) − δ(t) + 0. 5δ(t − 2) Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 18

Properties of Fourier Transform Let the FT of the triangular waveform be X(ω). Then, the FT of the impulses of d 2 x(t)/dt 2 : (0. 5 ej 2ω − 1 + 0. 5 e −j 2ω), must be equal to (jω)2 X(jω). That is, (0. 5 e+j 2ω − 1 + 0. 5 e−j 2ω) = cos(2ω) − 1 = − 2 sin 2(ω) = −ω2 X(ω) Solving for X(ω), we get the FT of the triangular waveform as Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 19

Properties of Fourier Transform 8 - Frequency-differentiation: Differentiating both sides of the FT definition with respect to ω yields The property is valid only if the resulting function is Fourier transformable. In general, As an example, solve for FT of te− 2 tu(t) Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 20

Properties of Fourier Transform 8 - Time-integration: Since integration is the inverse of differentiation, the above equation shows that the frequency domain operation corresponding to time-domain integration is multiplication by 1/jw, but an additional term is needed to account for a possible dc component in the integrator output. Hence, unless X(0) = 0, a dc component is produced by the integrator. Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 21