Fourier Transform CS 474674 Prof Bebis Sections 4

Fourier Transform CS 474/674 – Prof. Bebis Sections 4. 1, 4. 2, 4. 4, 4. 5, 4. 6

Image Transforms • Many times, image processing tasks can be best performed in a domain other than the spatial domain. • Key steps (1) Transform the image (2) Carry the task(s) in the transformed domain. (3) Apply inverse transform to return to the spatial domain.

Transformation Kernels • Forward Transformation forward transformation kernel • Inverse Transformation inverse transformation kernel

Kernel Properties • A kernel is said to be separable if: • A kernel is said to be symmetric if:

Trigonometric Fourier Series • Any periodic function f(t) can be expressed as a weighted (infinite) sum of sine and cosine functions of increasing frequency: basis functions where coefficients of expansion

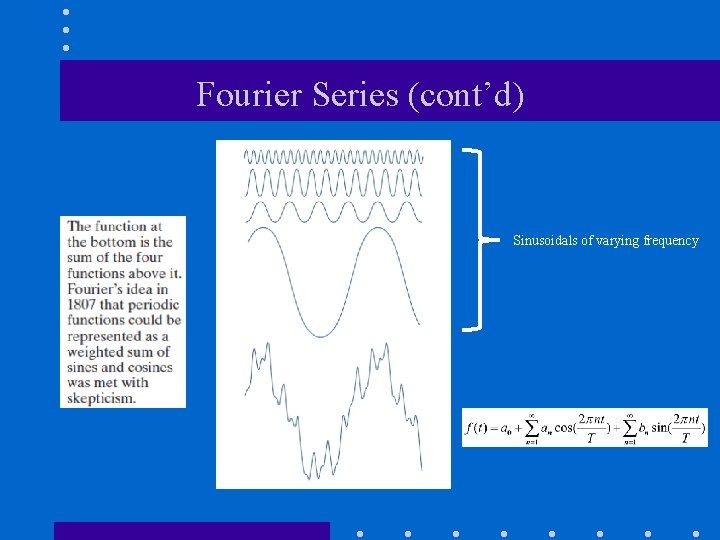
Fourier Series (cont’d) Sinusoidals of varying frequency

Exponential Fourier Series complex exponential Relationship to trigonometric series: where • The decomposition into sines and cosines is implied by Euler’s formula:

Continuous Fourier Transform (FT) • The Fourier Transform (FT) of a continuous, non-periodic function f(x) is defined as follows: • Given F(u), we can obtain f(x) back using the Inverse Fourier Transform (IFT): • If x represents time in seconds, the units of u are cycles/sec or Hertz (Hz).

FT - Definitions • F(u) is a complex function: • Magnitude of FT (or spectrum): • Phase of FT: • Magnitude-Phase representation: • Power of f(x): P(u)=|F(u)|2=

Why is FT Useful? • Easier to remove undesirable frequencies in the frequency domain. • Faster to perform certain operations in the frequency domain than in the spatial domain. – i. e. , using the Fast Fourier Transform (FFT)

Frequency Filtering: Main Steps 1. Take the FT of f(x): 2. Remove undesired frequencies: 3. Convert back to a signal: x We’ll talk more about these steps later. . . y

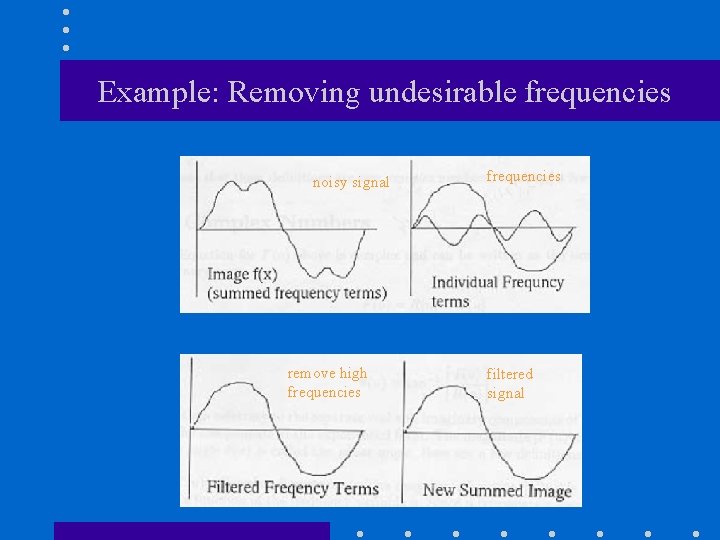
Example: Removing undesirable frequencies noisy signal remove high frequencies filtered signal

How do frequencies show up in an image? • Low frequencies correspond to slowly varying pixel intensities (e. g. , continuous surface). • High frequencies correspond to quickly varying pixel intensities (e. g. , edges) Original Image Low-passed image (i. e. , high frequencies removed)

Common FT Pairs See handouts posted on the course webpage!

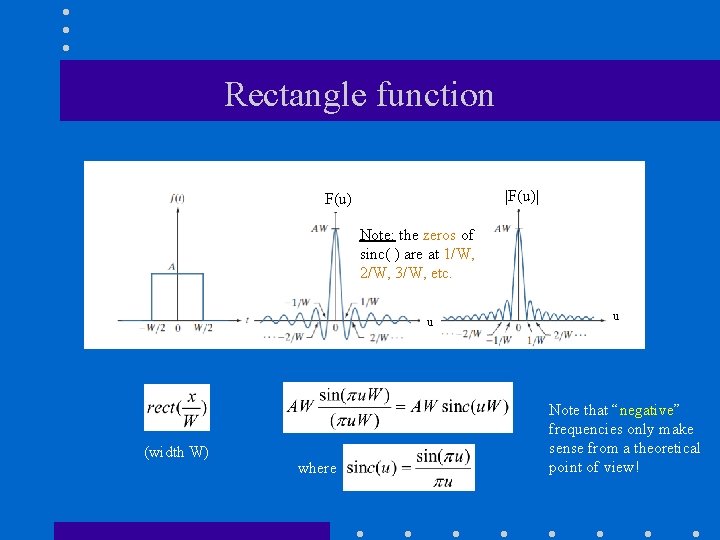
Rectangle function |F(u)| F(u) Note: the zeros of sinc( ) are at 1/W, 2/W, 3/W, etc. u (width W) where u Note that “negative” frequencies only make sense from a theoretical point of view!

Rectangle function (cont’d)

Duality Property f(x) F(u) f(-u) Prove it using the definition of the inverse FT! Note: if f(u) is even, then f(-u)=f(u)

Duality Property (cont’d)

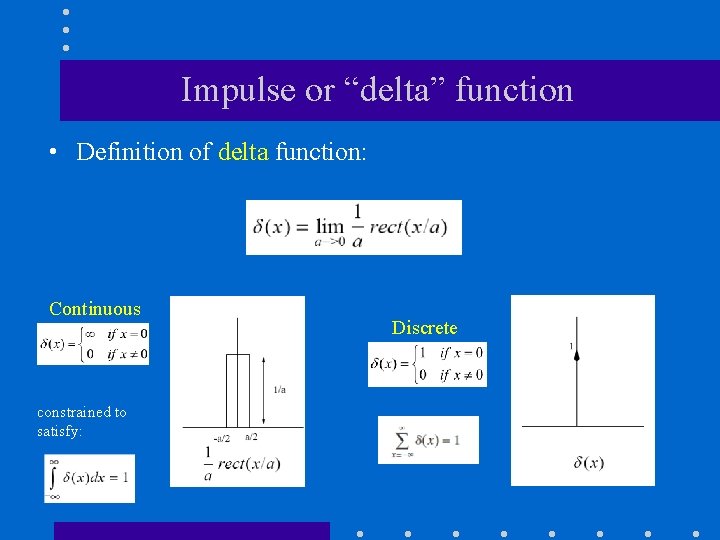
Impulse or “delta” function • Definition of delta function: Continuous constrained to satisfy: Discrete

Impulse (“delta”) (cont’d) • Properties: Continuous Discrete

What is the FT of δ(x)? 1 x u

“Train” of impulses or “deltas” function • An infinite sum of impulses, Δx units apart:

What is the FT of a s(x)? • It is also a “train” of impulses, Δu=1/Δx units apart: (see pages 258 -259 for a proof)

Spatial/frequency shifts (translation) Special Cases:

Spatial/frequency shifts (cont’d)

Cosine function • FT of the cosine function: Note: the imaginary part is zero; this is true for all real and even f(x) cos(2πu 0 x) F(u) 1/2 Note that “negative” frequencies only make sense from a theoretical point of view!

Cosine function (cont’d)

Sine function • FT of the sine function: Note: the real part is zero; this true for all real and odd f(x) imaginary axis j. F(u) sin(2πu 0 x) Note that “negative” frequencies only make sense from a theoretical point of view!

Extending FT in 2 D • Forward FT • Inverse FT

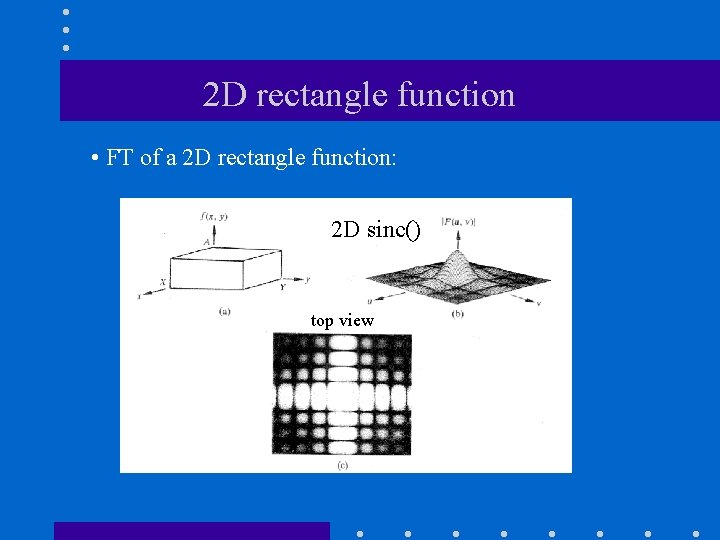
2 D rectangle function • FT of a 2 D rectangle function: 2 D sinc() top view

Discrete Fourier Transform (DFT) • Extending the Fourier Transform to the discrete case requires manipulating discrete functions. • We need to discuss sampling first! f(x) F(u) Δx: sampling step in the spatial domain (assuming x 0=0) Δu: sampling step in the frequency domain

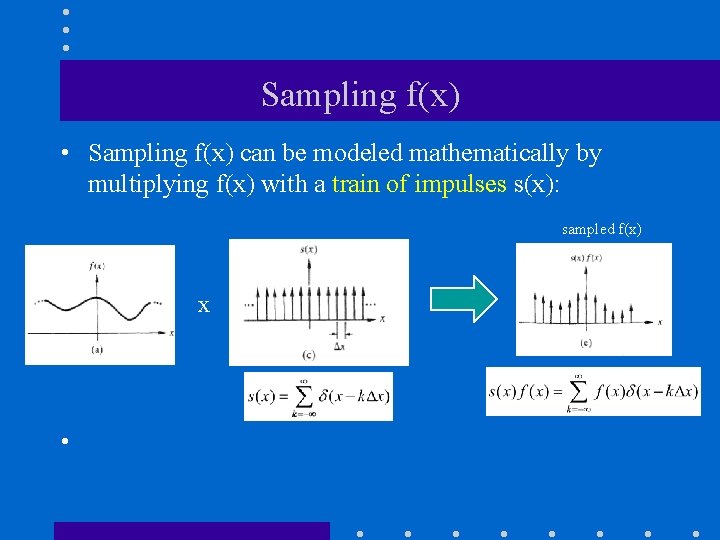
Sampling f(x) • Sampling f(x) can be modeled mathematically by multiplying f(x) with a train of impulses s(x): sampled f(x) x •

What is the FT of s(x)f(x) ? • Using the FT definition:

What is the FT of s(x)f(x)? (cont’d) • We will show later that the FT of s(x)f(x) is periodic with period 1/Δx – i. e. , need to sample one period only. • Assuming N equally spaced samples in the frequency domain u, then the sampling step Δu would be: where • Substituting, we obtain the DFT:

Discrete Fourier Transform (DFT) • Forward DFT • Inverse DFT

Discrete Fourier Transform (DFT) (cont’d) • Using same notation as in the continuous case: Forward DFT Inverse DFT where: l u (u-th sample) and k x (x-th sample)

Discrete Fourier Transform (DFT) (cont’d) • We will be using the equivalent definition below where the 1/N constant appears in the forward DFT instead of the inverse DFT: Forward DFT Inverse DFT

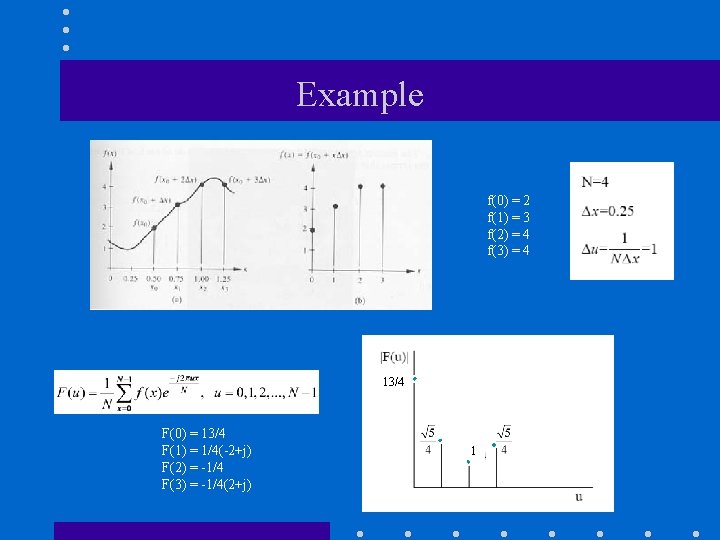
Example f(0) = 2 f(1) = 3 f(2) = 4 f(3) = 4 13/4 F(0) = 13/4 F(1) = 1/4(-2+j) F(2) = -1/4 F(3) = -1/4(2+j) 1

Example (cont’d)

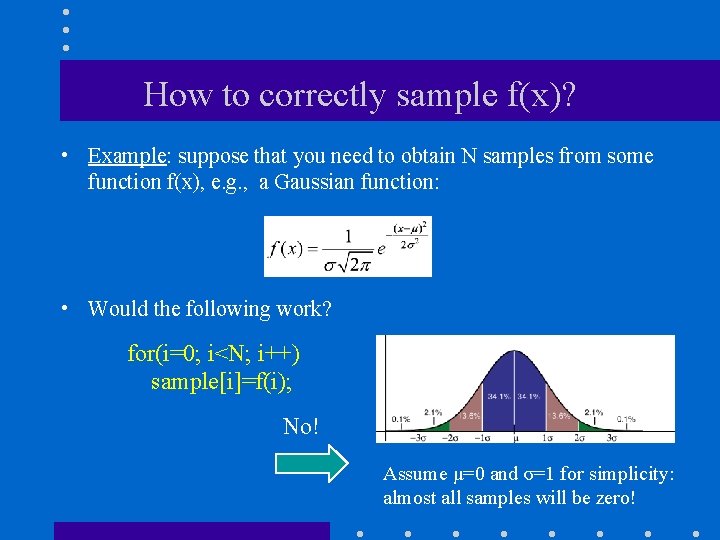
How to correctly sample f(x)? • Example: suppose that you need to obtain N samples from some function f(x), e. g. , a Gaussian function: • Would the following work? for(i=0; i<N; i++) sample[i]=f(i); No! Assume μ=0 and σ=1 for simplicity: almost all samples will be zero!

How to correctly sample f(x)? (cont’d) 1. Determine effective sampling range: [μ-3σ, μ+3σ]=[a, b] 2. Determine sampling step: Δx = (b-a)/N 3. Obtain the samples: for(i=0; i<N; i++) sample[i]=f(a+iΔx);

Extending DFT to 2 D • Assume that f(x, y) is M x N: • Forward DFT • Inverse DFT:

Extending DFT to 2 D (cont’d) • Special case: f(x, y) is N x N: • Forward DFT • Inverse DFT

Extending DFT to 2 D (cont’d) Interpretation: 2 D cos/sin functions

How to visualize DFT? • Typically, we visualize the magnitude/spectrum: |F(u, v)| • The dynamic range of |F(u, v)| is typically very large! (c is a user-defined constant for improving visualization) • Apply stretching: original image |F(u, v)| |D(u, v)| before stretching after stretching

How to visualize DFT? (cont’d) • The transformation below needs to be applied only for visualizing the spectrum of DFT. • It does not change the information conveyed by the spectrum, it only allows us to better visualize it! (c is a user-defined constant for improving visualization)

DFT Properties: (1) Separability • The 2 D DFT can be computed using 1 D DFTs: Forward DFT: kernel is separable:

DFT Properties: (1) Separability (cont’d) • Rewrite F(u, v) as follows: • Let’s set: • Then: Steps: 1. Compute F(x, v) 2. Compute F(u, v)

DFT Properties: (1) Separability (cont’d) • How to compute F(x, v)? ) x, v=0, 1, 2, …N-1 N x DFT of the rows of f(x, y) • How to compute F(u, v)? u, v=0, 1, 2, …N-1 DFT of the cols of F(x, v)

DFT Properties: (1) Separability (cont’d) Computing 2 D DFT using 1 D DFTs: f(x, y) F(x, v) F(u, v)

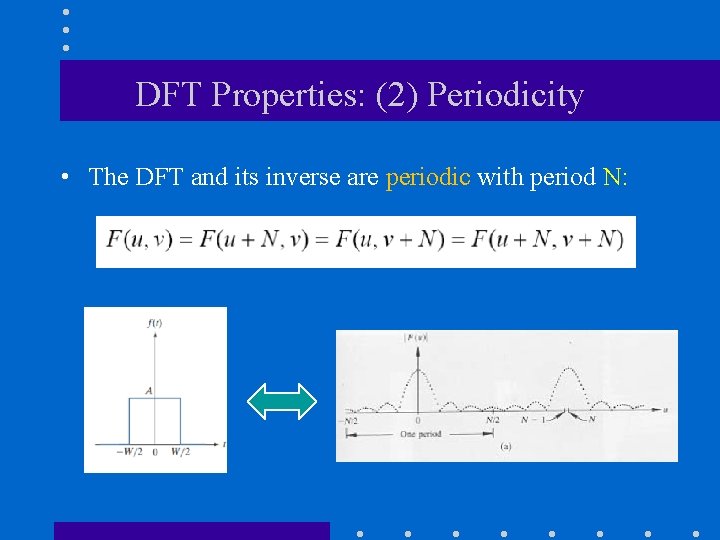
DFT Properties: (2) Periodicity • The DFT and its inverse are periodic with period N:

DFT Properties: (2) Periodicity (cont’d) =F(u, v)

DFT Properties: (3) Symmetry

DFT Properties: (4) Translation f(x, y) F(u, v) • Translation in spatial domain: • Translation in frequency domain: ) N

DFT Properties: (4) Translation (cont’d) • To “see” a full period, we need to translate the origin of the transform to N/2 (or to (N/2, N/2) in 2 D) |F(u)| after translation |F(u-N/2)|

DFT Properties: (4) Translation (cont’d) • Use the following property to compute F(u-N/2, v-N/2): ) N • This leads us to the following property:

DFT Properties: (4) Translation (cont’d) sinc before translation after translation

DFT Properties: (5) Rotation • Rotating f(x, y) by θ rotates F(u, v) by θ

DFT Properties: (6) Addition/Multiplication

DFT Properties: (7) Scale

DFT Properties: (8) Average value Average: F(u, v) at u=0, v=0: So:

Magnitude and Phase of DFT • What is more important? magnitude phase • Hint: use the inverse DFT to reconstruct the input image using only magnitude or phase information

Magnitude and Phase of DFT (cont’d) Reconstructed image using magnitude only (i. e. , magnitude determines the strength of each sinusoidal component) Reconstructed image using phase only (i. e. , phase determines the phase of each sinusoidal component)

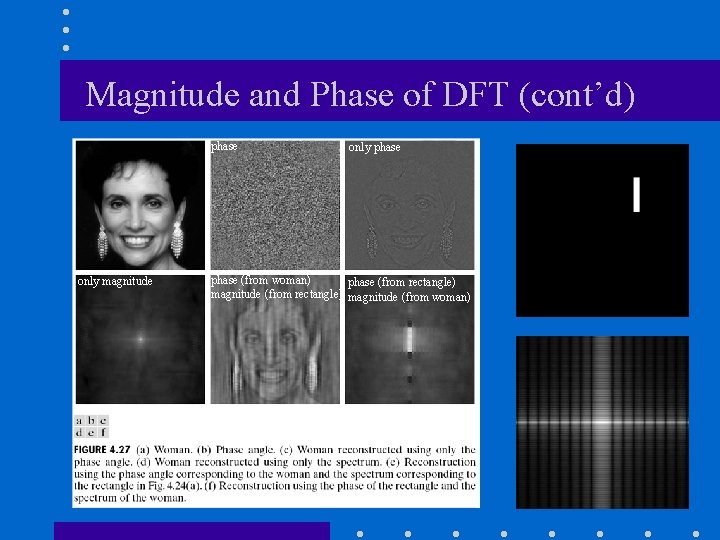
Magnitude and Phase of DFT (cont’d) phase only magnitude only phase (from woman) phase (from rectangle) magnitude (from woman)

Quiz #4 • When: Wednesday (Nov 4 th) at 2 pm • What: Fourier Transform (continuous and discrete) • Duration – 10 minutes for answering questions – 5 minutes for uploading your answers on Canvas • Suggested Apps – Genius Scan https: //thegrizzlylabs. com/genius-scan/ – Canvas Student https: //apps. apple. com/us/app/canvas-student/id 480883488