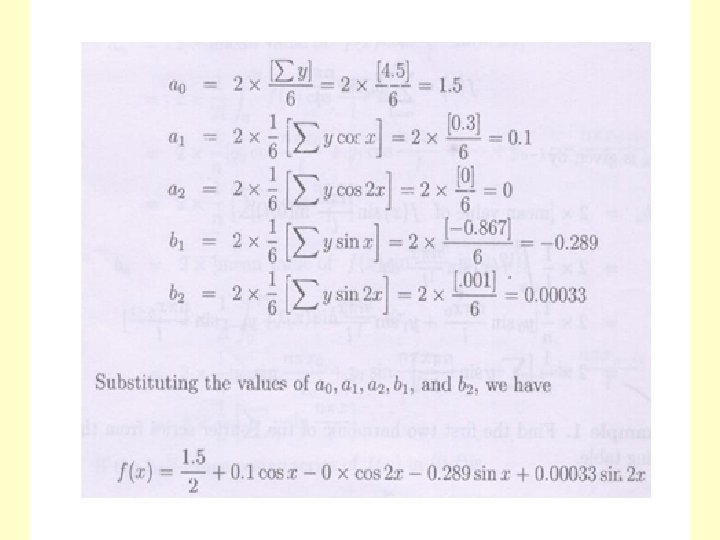FOURIER SERIES PERIODIC FUNCTIONS A function fx is










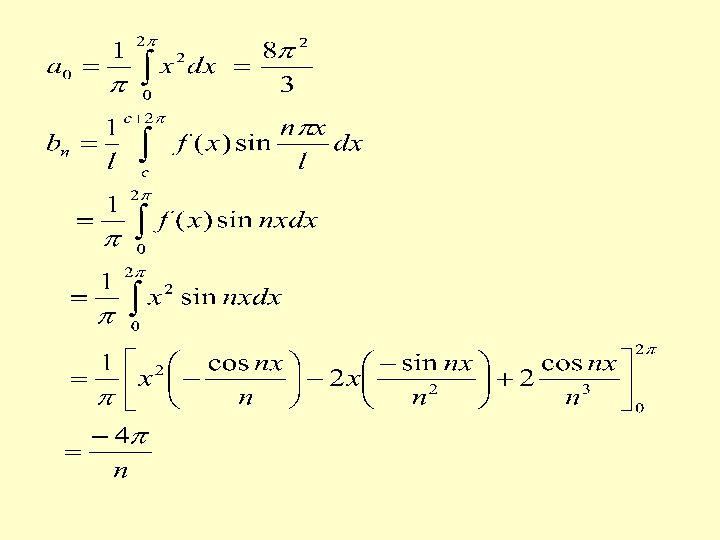




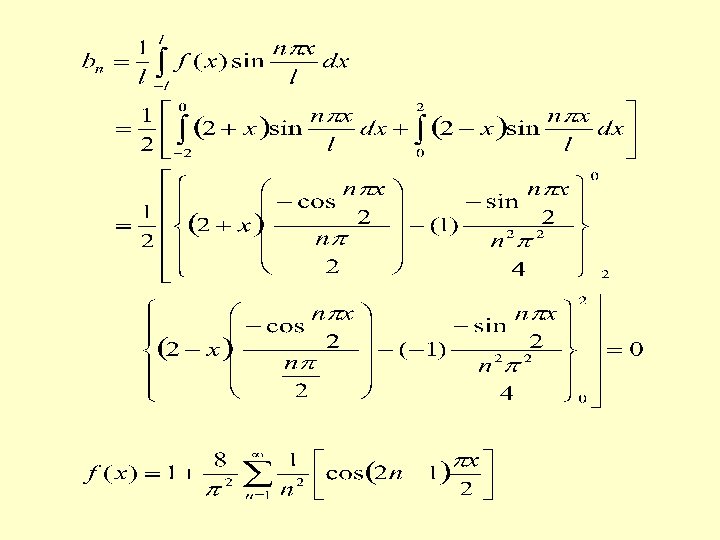



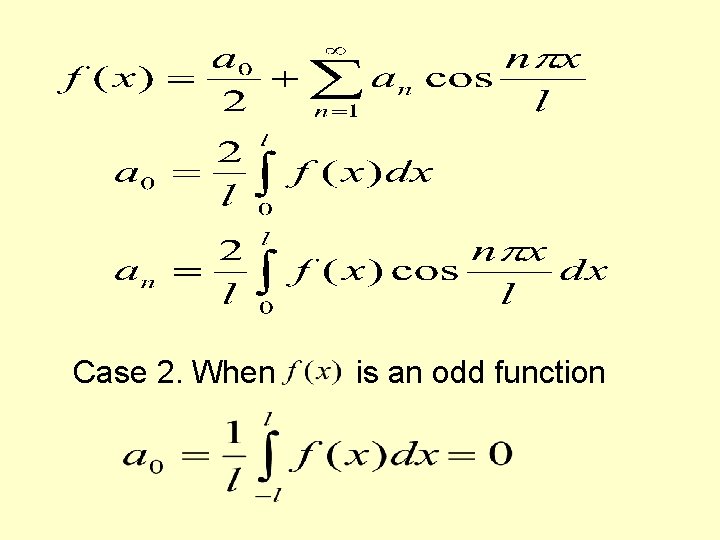


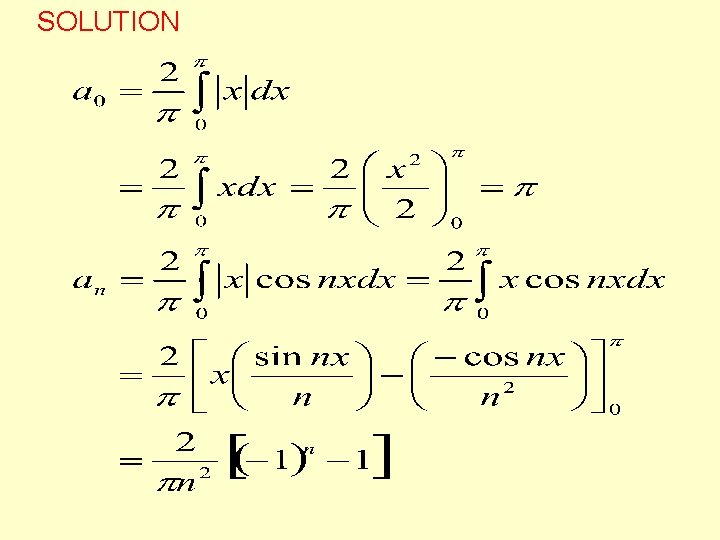



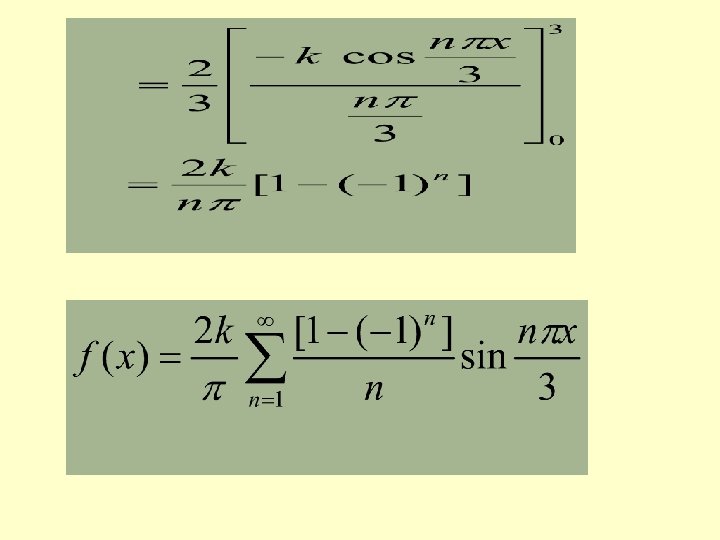
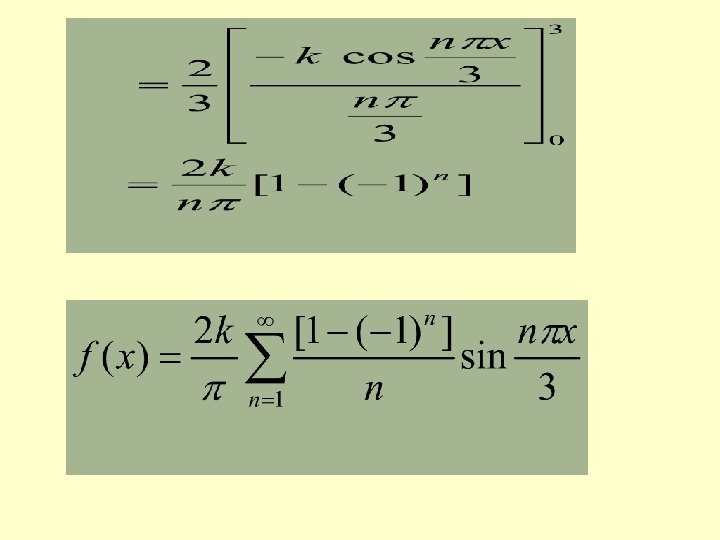
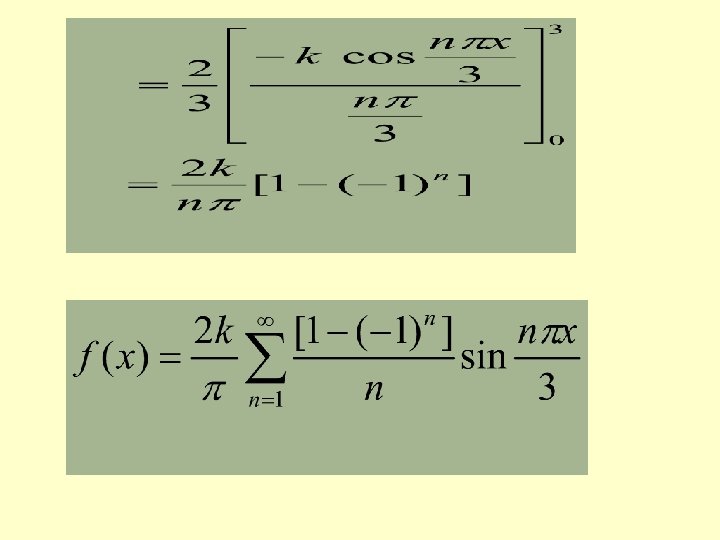



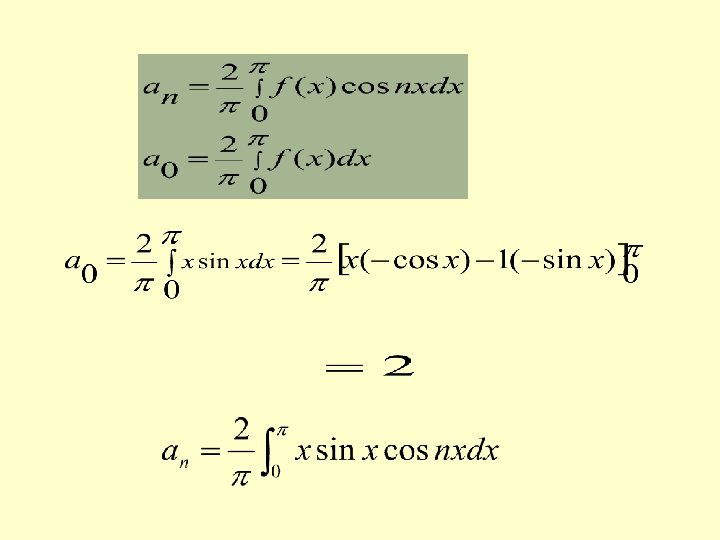
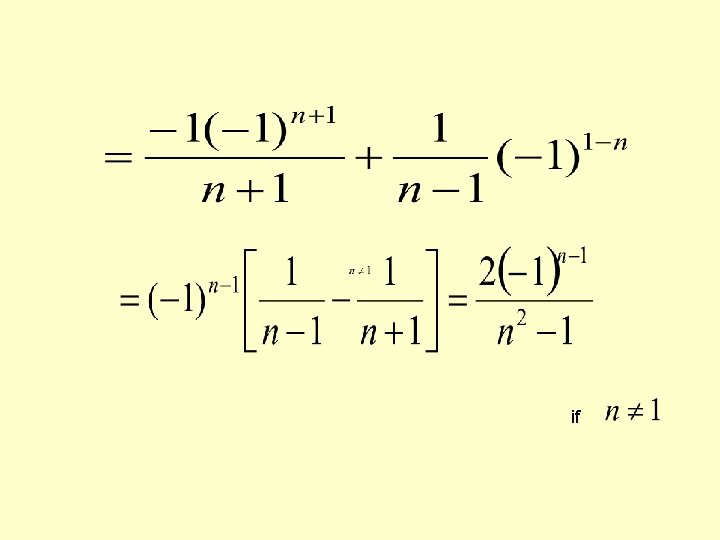
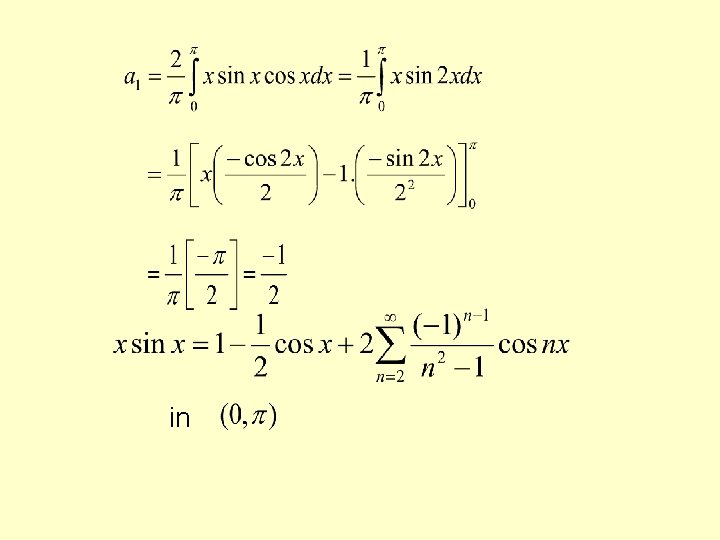
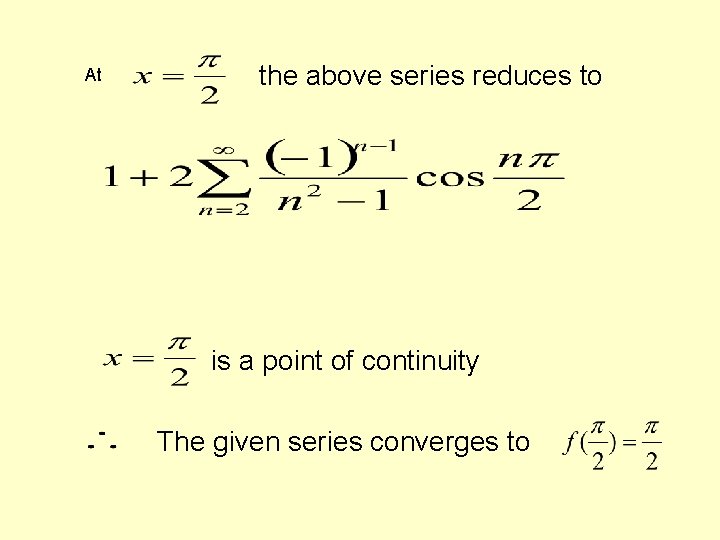
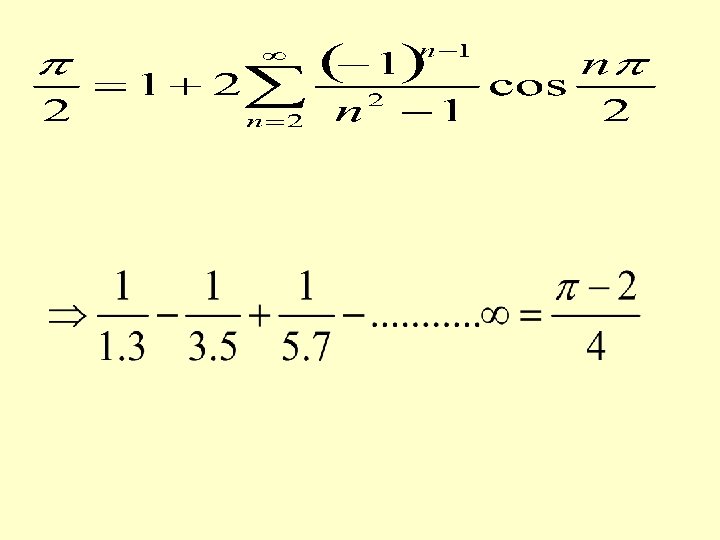

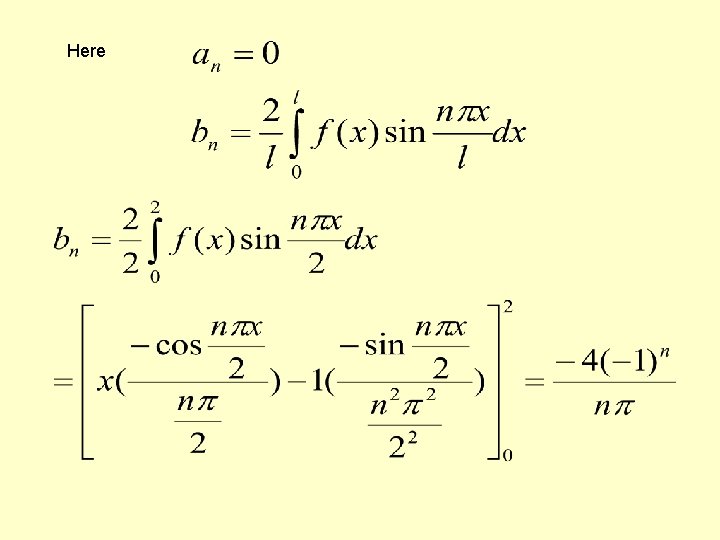

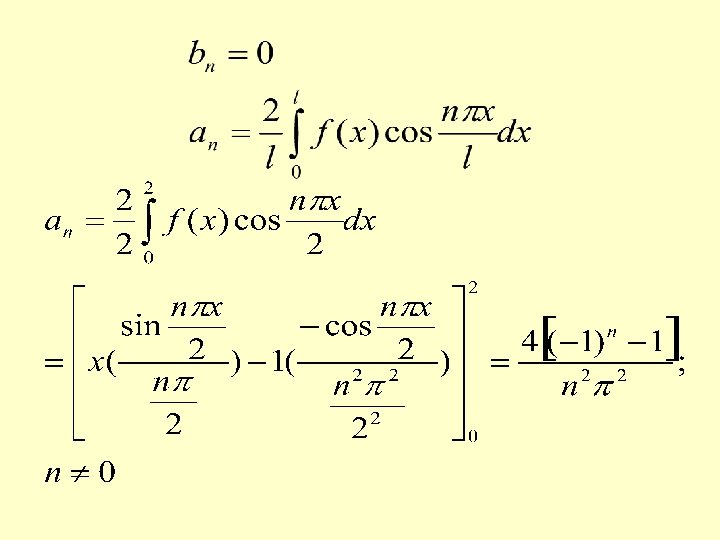
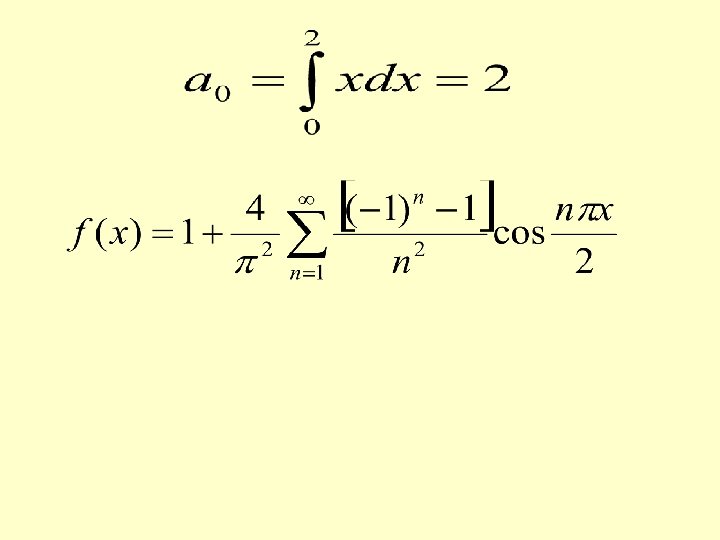




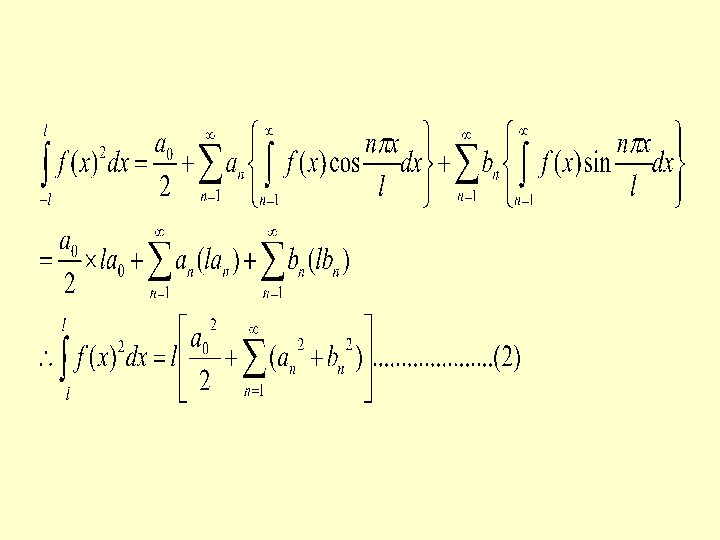




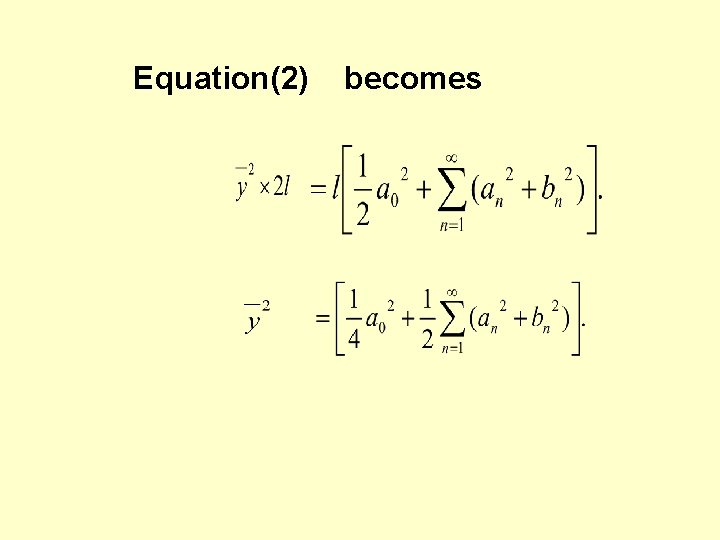





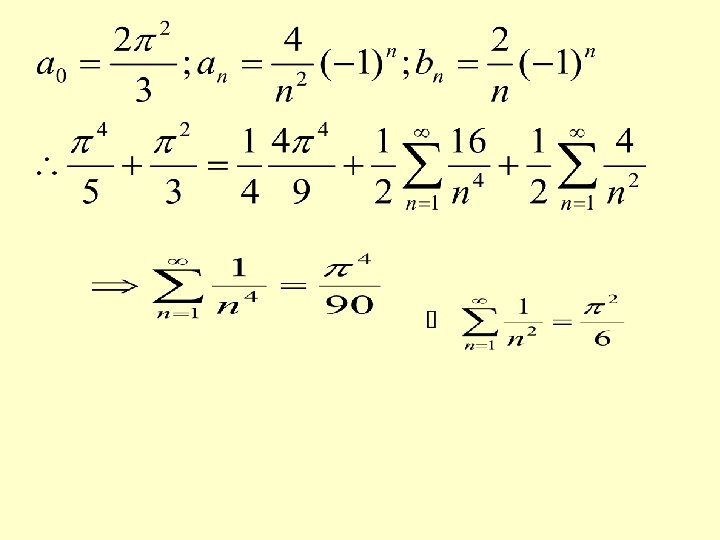


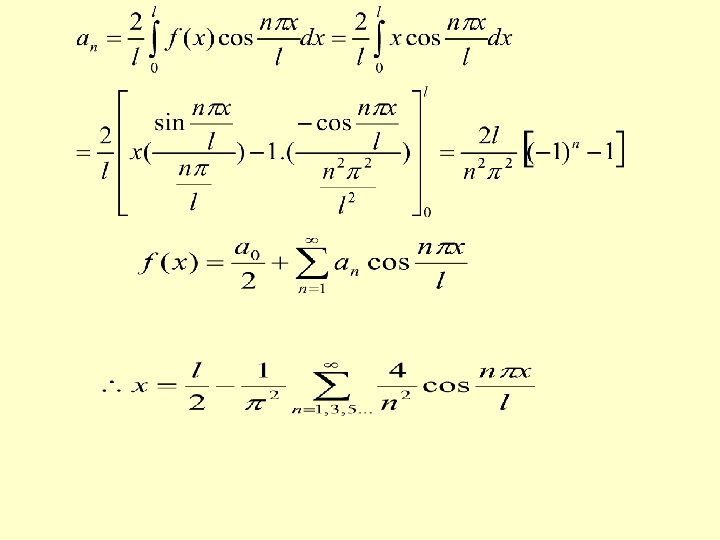







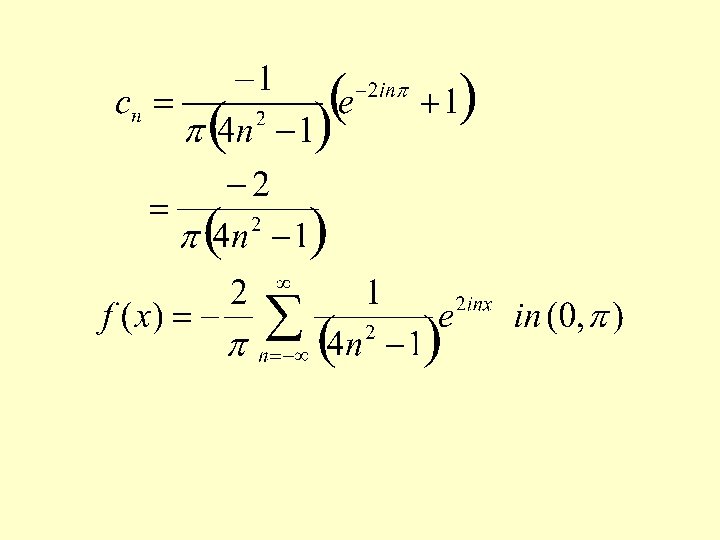

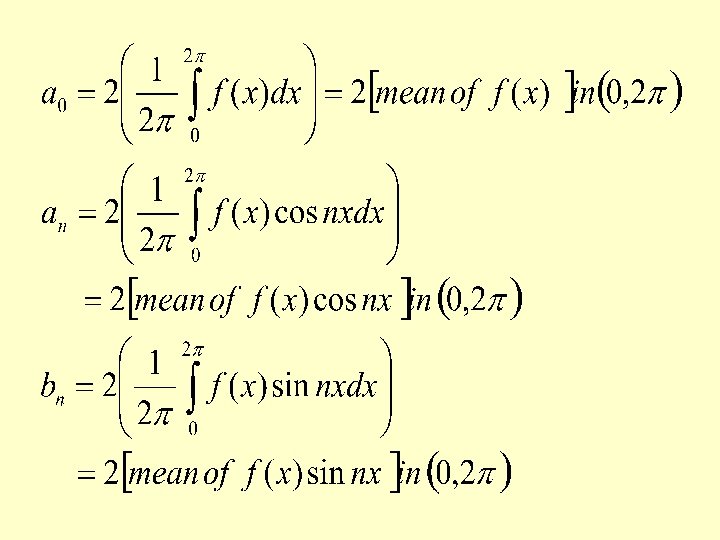

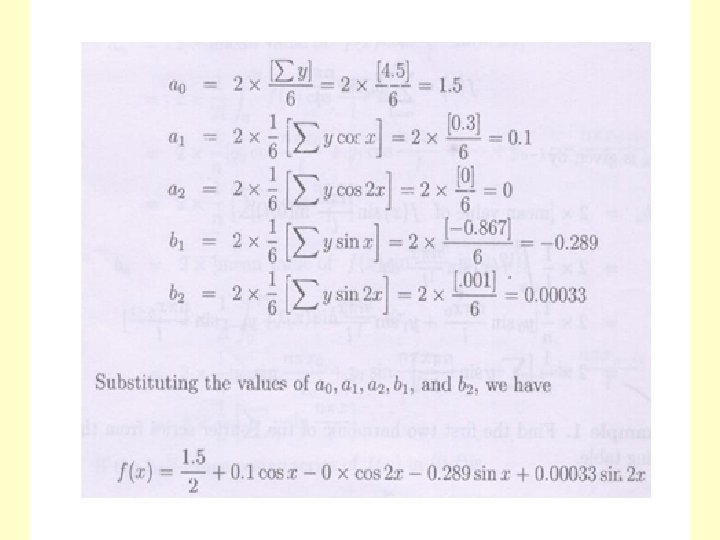
- Slides: 81

FOURIER SERIES PERIODIC FUNCTIONS A function f(x) is said to be periodic with period T if f(x+T)=f(x) x , where T is a positive constant. The least value of T>0 is called the period of f(x).

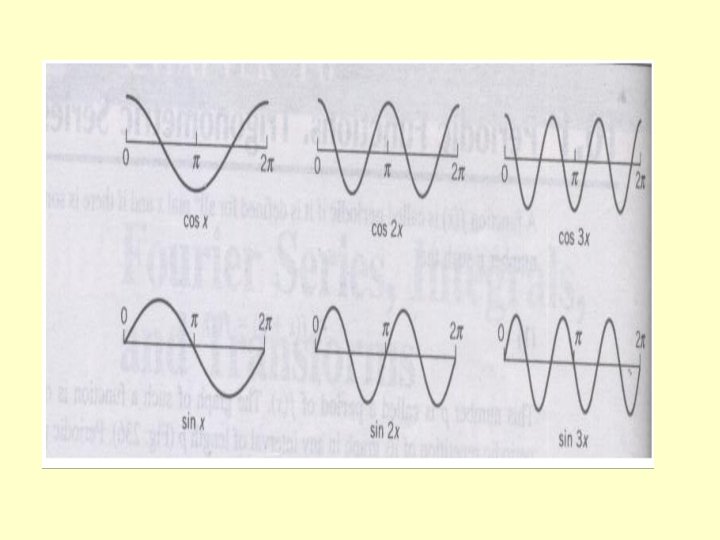
f(x+2 T) =f ((x+T)+T) =f (x+T)=f(x) f(x+n. T)=f(x) for all x Ex. 1 f(x)=sin x has periods 2 , 4 , 6 , …. and 2 is the period of f(x). Ex. 2 The period of sin nx and cos nx is 2 /n.


FOURIER SERIES

where the Fourier coeffecients are

If is defined in the interval (c, c+2 ), the coefficients can be determined equivalently from

DIRICHLET CONDITIONS Suppose that 1. f(x) is defined and single valued except possibly at finite number of points in (-l, +l) 2. f(x) is periodic outside (-l, +l) with period 2 l 3. f(x) and f’(x) are piecewise continuous in(-l, +l)

Then the Fourier series of f(x) converges to a) f(x) if x is a point of continuity b)[f(x+0)+f(x-0)]/2 if x is a point of discontinuity

METHOD OF OBTAINING FOURIER SERIES OF 1. 2. 3. 4.

SOLVED PROBLEMS 1. Expand f(x)=x 2, 0<x<2 in Fourier series if the period is 2 . Prove that


SOLUTION Period = 2 thus c=0 = and choosing
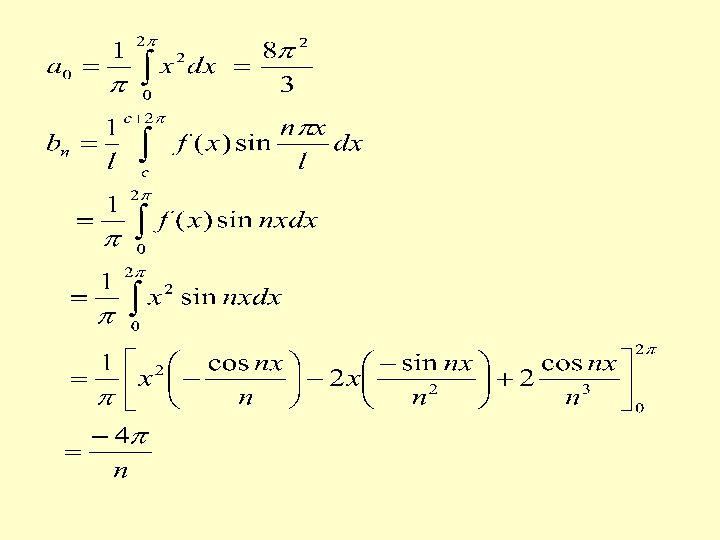

At x=0 the above Fourier series reduces to X=0 is the point of discontinuity

By Dirichlet conditions, the series converges at x=0 to (0+4 2)/2 = 2 2

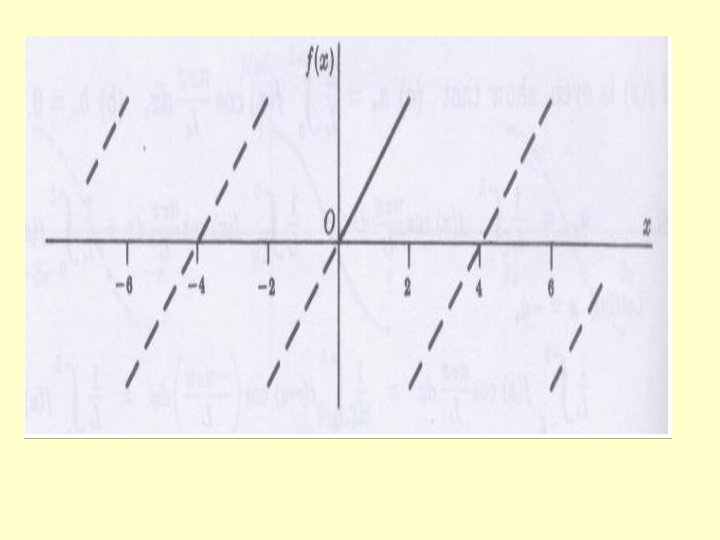
2. Find the Fourier series expansion for the following periodic function of period 4. Solution

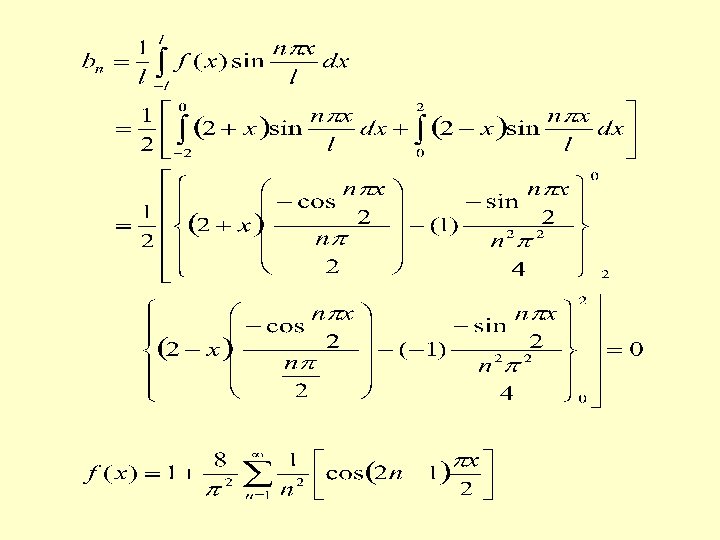

EVEN AND ODD FUNCTIONS A function f(x) is called odd if f(-x)=-f(x) Ex: x 3, sin x, tan x, x 5+2 x+3 A function f(x) is called even if f(-x)=f(x) Ex: x 4, cos x, ex+e-x, 2 x 6+x 2+2

EXPANSIONS OF EVEN AND ODD PERIODIC FUNCTIONS If is a periodic function defined in the interval , it can be represented by the Fourier series Case 1. If is an even function

If a periodic function is even in , its Fourier series expansion contains only cosine terms
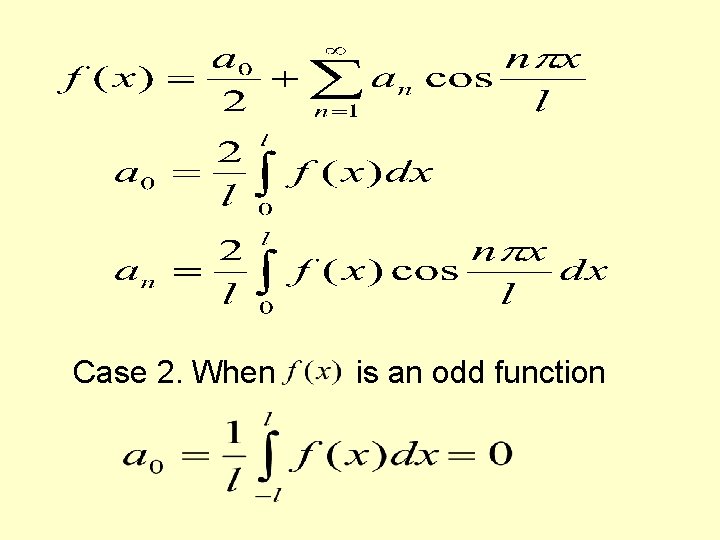
Case 2. When is an odd function

If a periodic function is odd in , its Fourier expansion contains only sine terms

SOLVED PROBLEMS 1. For a function defined by obtain a Fourier series. Deduce that Solution is an even function
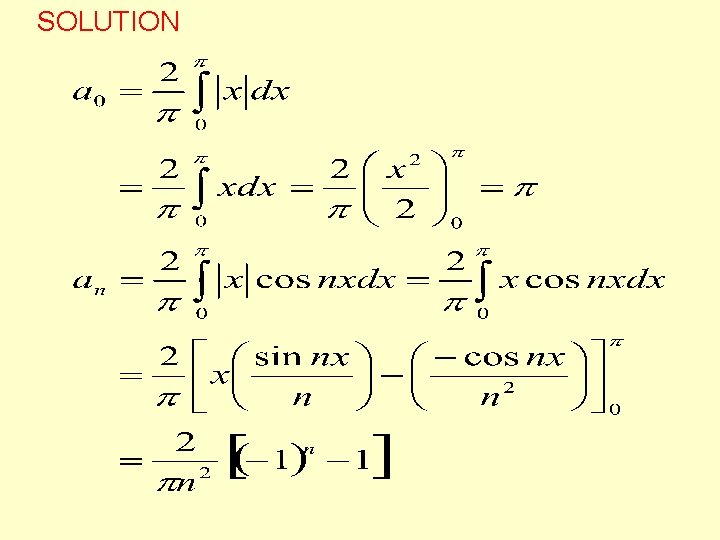
SOLUTION

At x=0 the above series reduces to x=0 is a point of continuity, by Dirichlet condition the Fourier series converges to f(0) and f(0)=0

PROBLEM 2 Is the function even or odd. Find the Fourier series of f(x)

SOLUTION is odd function
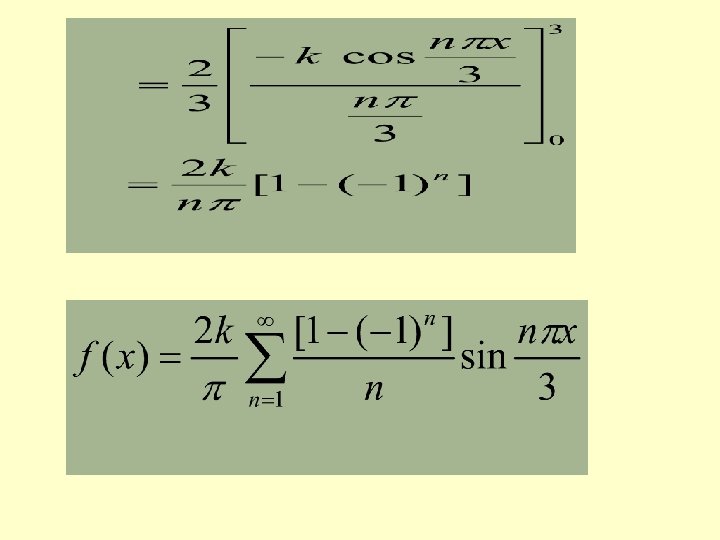
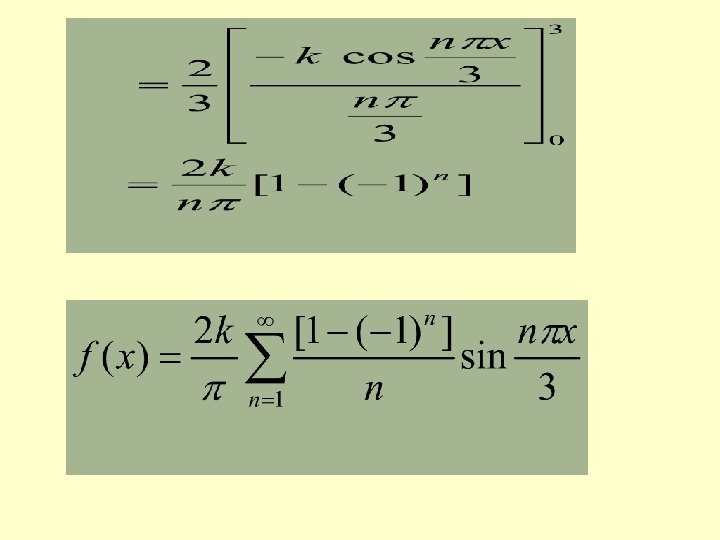
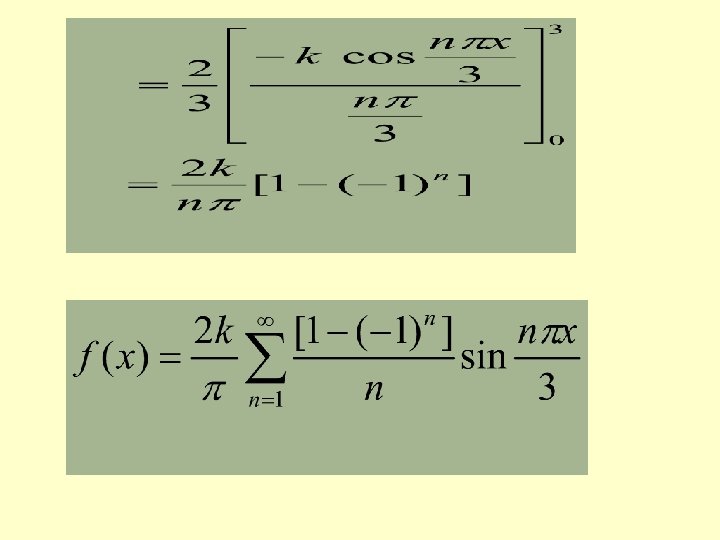

HALF RANGE SERIES COSINE SERIES A function defined in can be expanded as a Fourier series of period containing only cosine terms by extending suitably in. (As an even function)

SINE SERIES A function defined in can be expanded as a Fourier series of period containing only sine terms by extending suitably in [As an odd function]

SOLVED PROBLEMS Obtain the Fourier expansion of (x sinx )as a cosine series in. Hence find the value of SOLUTION Given function represents an even function in
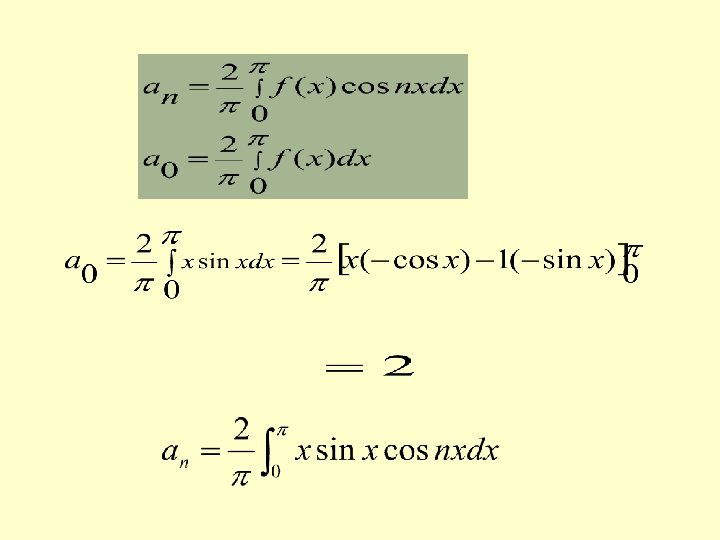
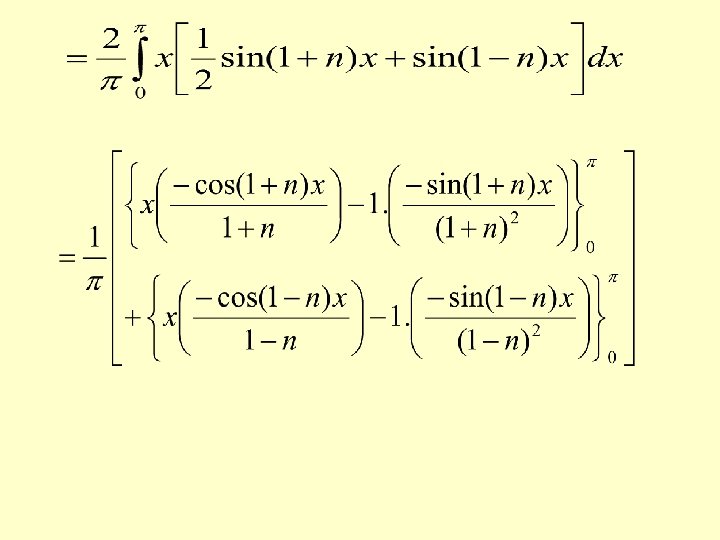
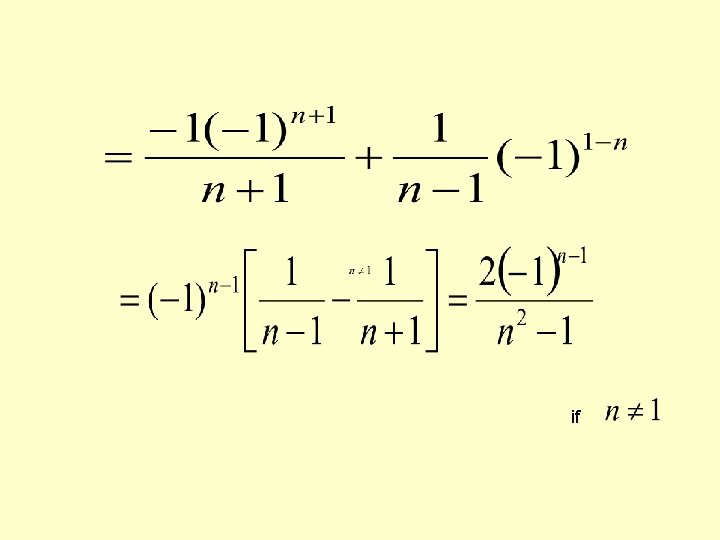
if
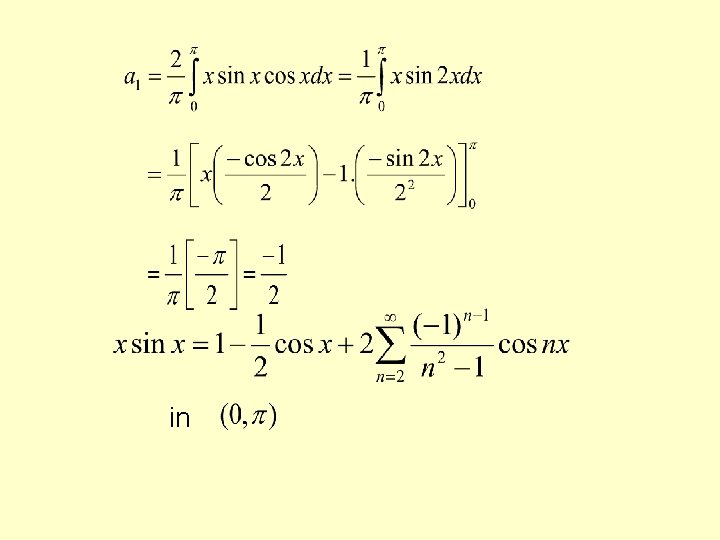
in
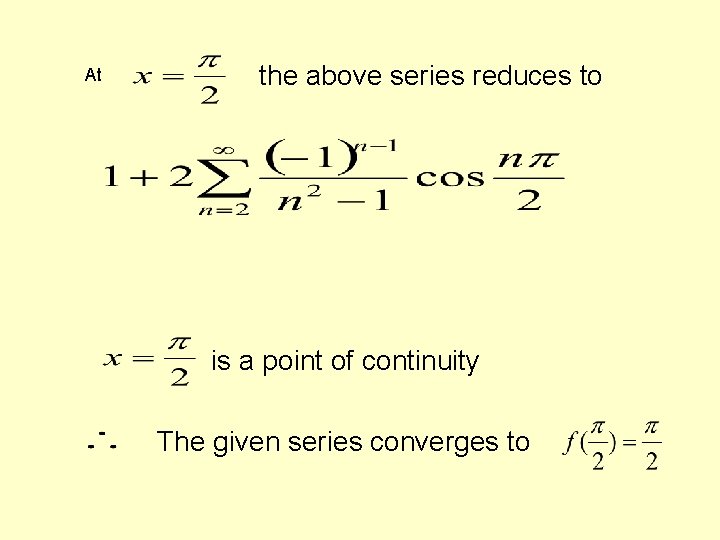
At the above series reduces to is a point of continuity The given series converges to
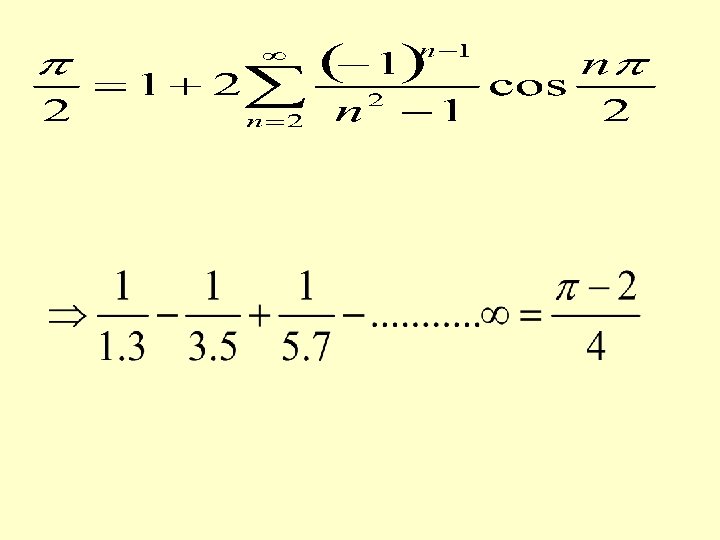

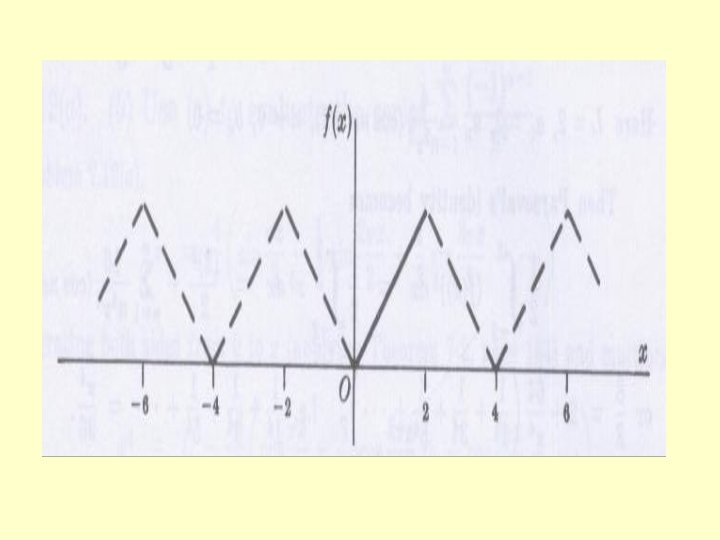
2) Expand in half range (a) sine Series (b) Cosine series. SOLUTION (a) Extend the definition of given function to that of an odd function of period 4 i. e

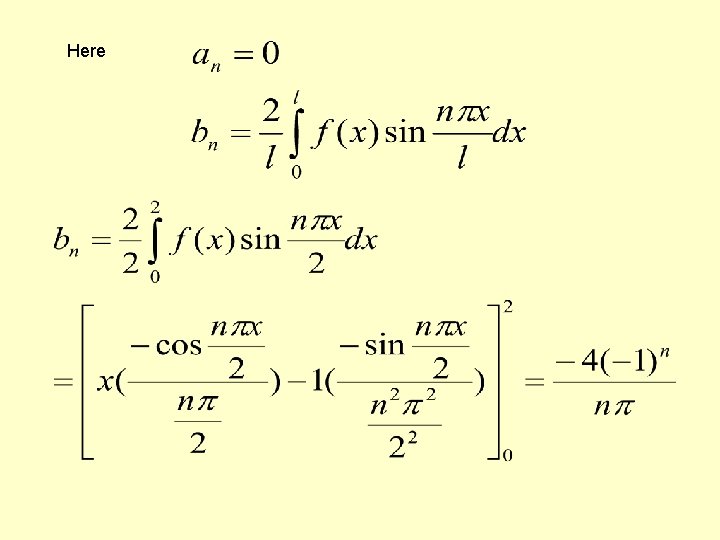
Here

(b) Extend the definition of given function to that of an even function of period 4

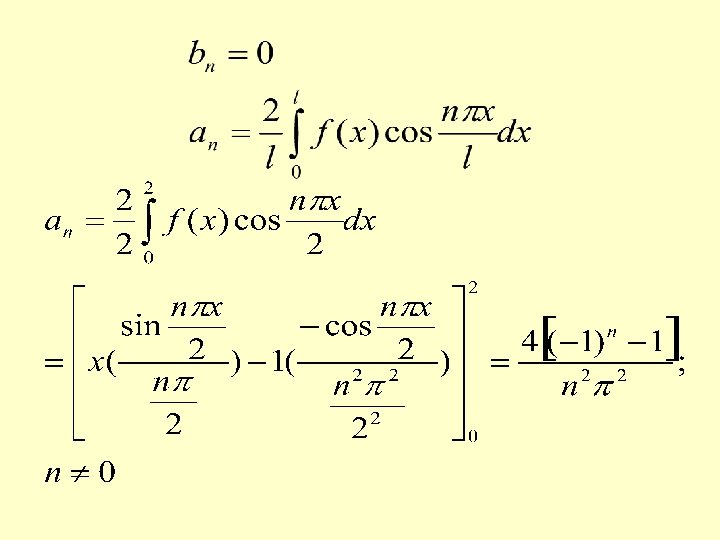
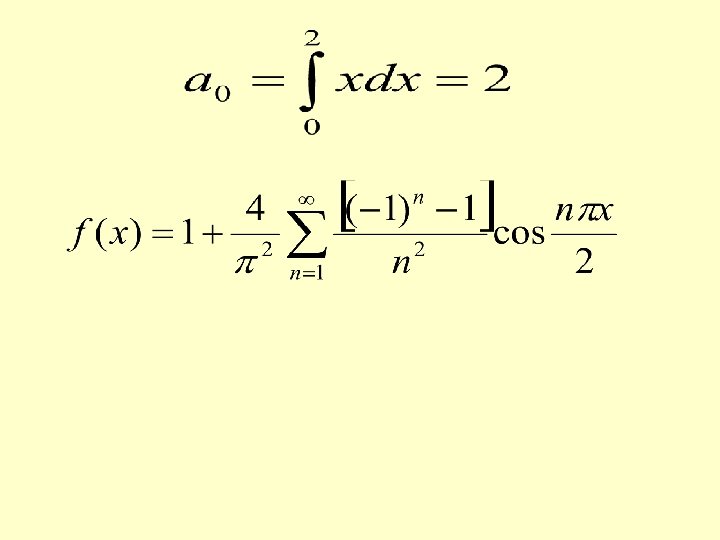

Exercise problems 1. Find Fourier series of 2. in Find Fourier series of

3. Find the Fourier series of in 4. Find the Fourier series of in (-2 , 2)

5. Represent function In (0, L) by a Fourier cosine series 6. Determine the half range sine series for

PARSEVAL’S IDENTITY • To prove that Provided the Fourier series for f(x) converges uniformly in (-l, I). The Fourier Series for f(x) in (-l, l) is Multiplying both sides of (1) by f(x)and integrating term from – l to l ( which is justified because f(x) is uniformly convergent)
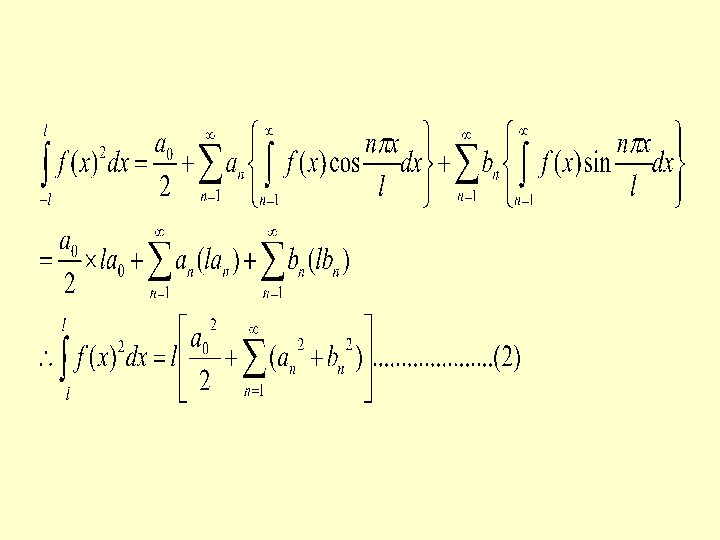

CASE-I If f(x) is defined in (0, 2 l) then Parseval’s Identity is given by

CASE-II If half range cosine series in (o, l) for f(x) is. Then Parseval’s Identity is given by .

CASE-III If the half range Sine sereies in (0, l) for f(x) is Then Parseval, s Identity is given by

RMS VALUE OF FUNCTION If a function y=f(x) is defined in ( c , c+2 l ), then is called the root mean square value (RMS value) of y in ( c , c+2 l ). It is denoted by .
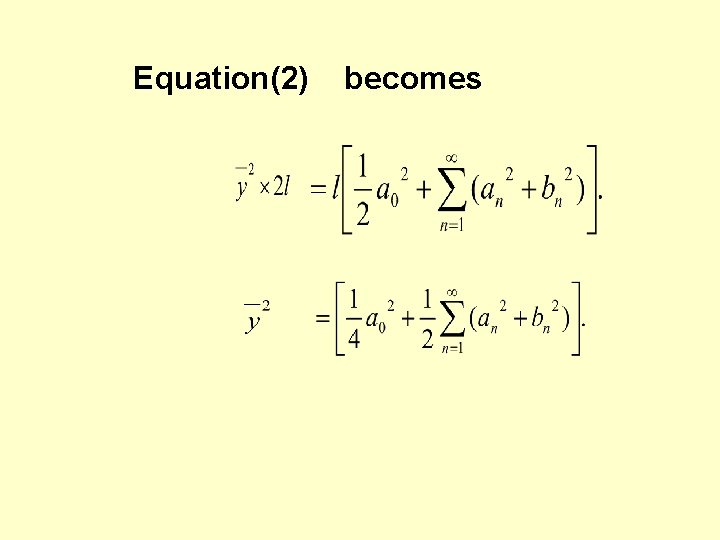
Equation(2) becomes
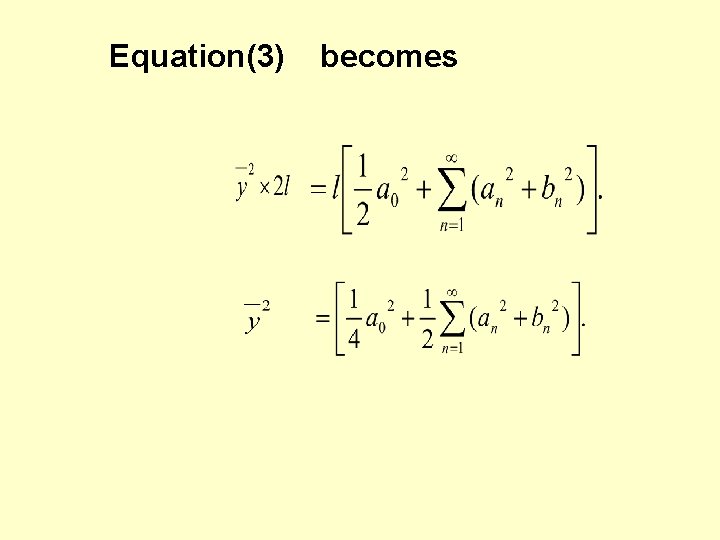
Equation(3) becomes

Equation(4) becomes Equation(5)becomes

SOLVED PROBLEMS 1) Find the Fourier series of periodic function in Hence deduce the sum of series Assuming that

SOLUTION in

if is odd function

Using the Parseval’s Identity
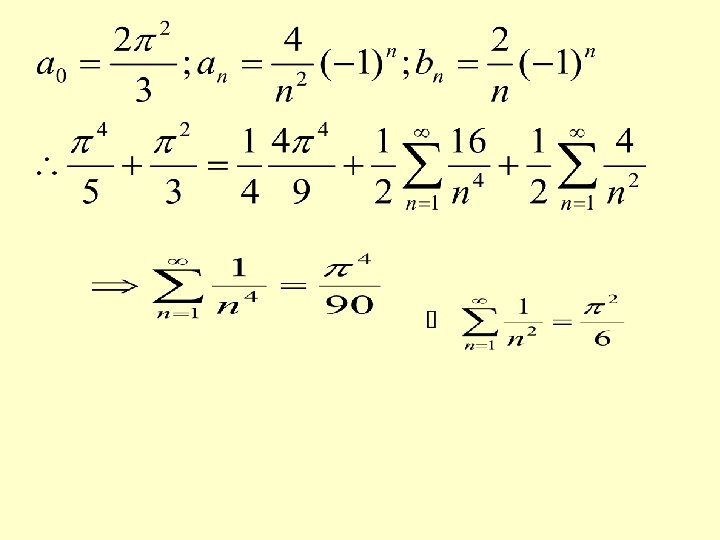

i 2)By using sine series for Show that SOLUTION for in

By Parseval’s Identity

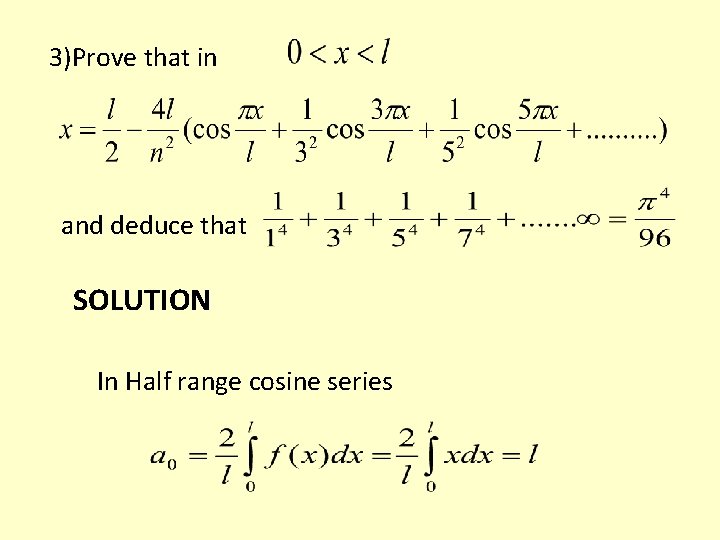
3)Prove that in and deduce that SOLUTION In Half range cosine series
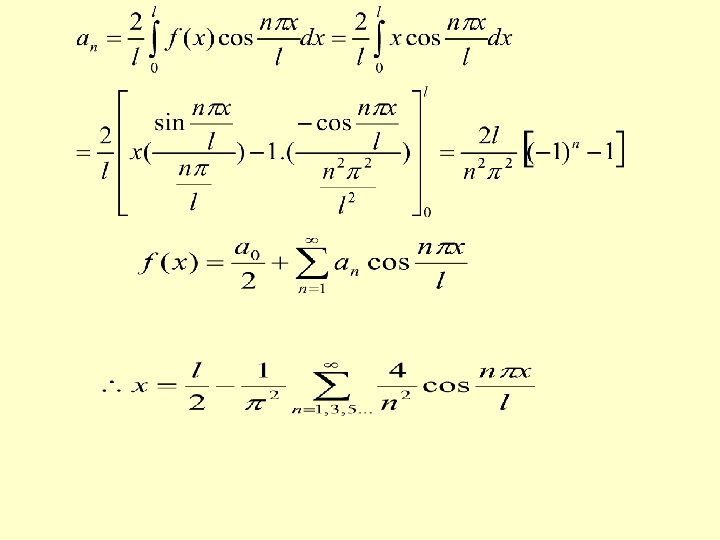

By Parseval’s Identity

COMPLEX FORM OF FOURIER SERIES The Fourier series of a periodic function of period 2 l is

The Fourier series can be represented in the following way

SOLVED PROBLEM 1. Find the complex form of the Fourier series of the periodic function

SOLUTION

2. Find the complex form of Fourier seriesof f(x)=sinx in (0, )

SOLUTION
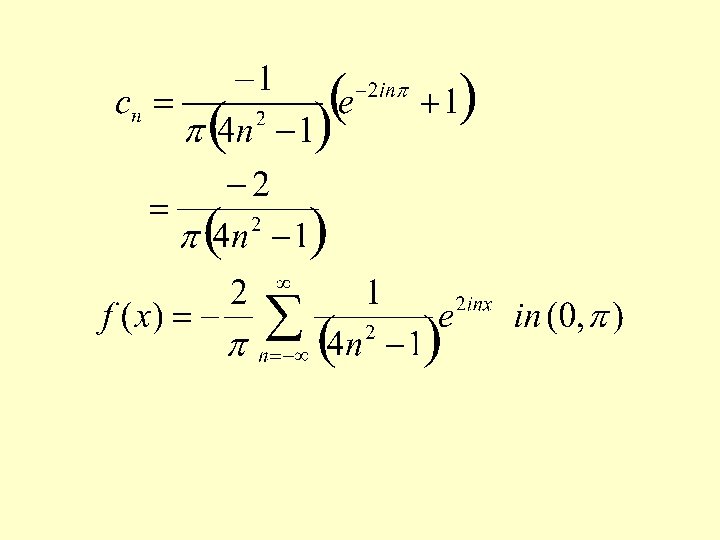

HARMONIC ANALYSIS
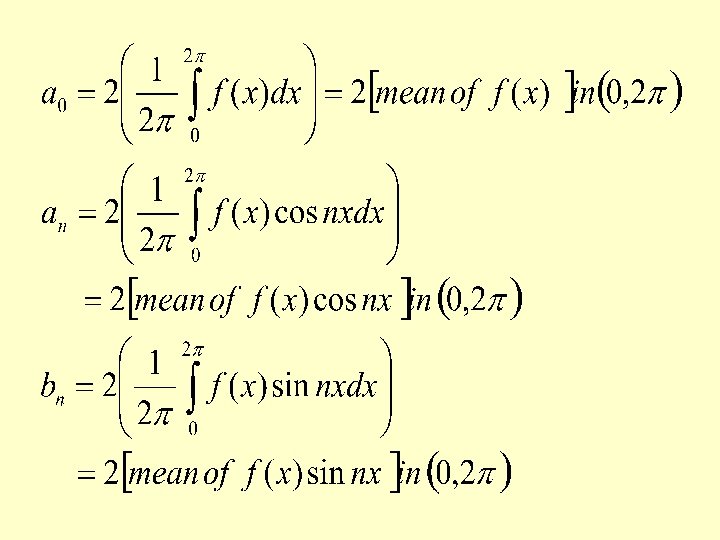

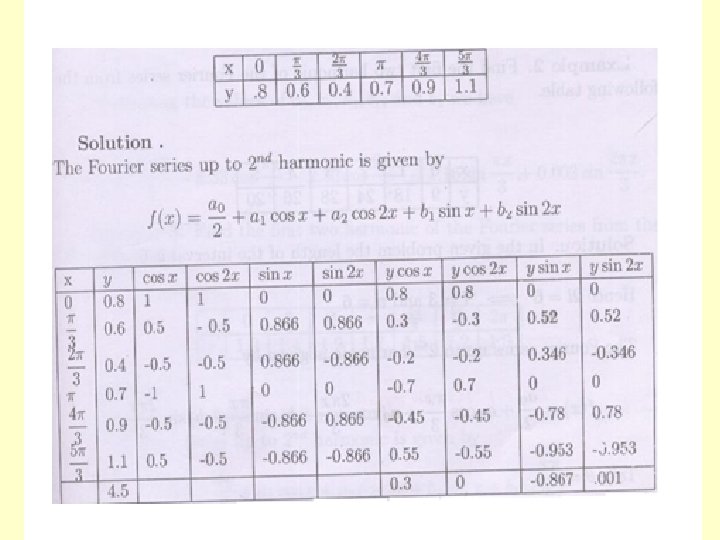
The term a 1 cosx+b 1 sinx is called the fundamental or first harmonic, the term a 2 cosx+b 2 sinx is called the second harmonic and so on. Solved Problem 1. Find first two harmonics of Fourier Series from the following table