Fourier Series Content Periodic Functions l Fourier Series

































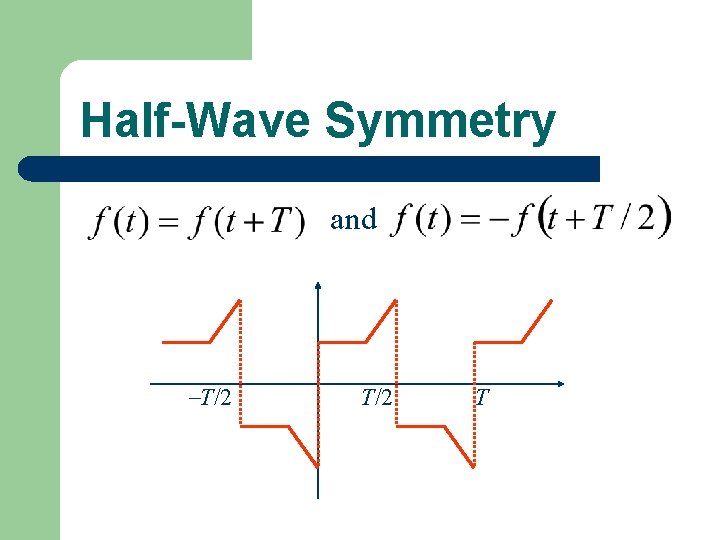














- Slides: 74

Fourier Series 主講者:虞台文

Content Periodic Functions l Fourier Series l Complex Form of the Fourier Series l Impulse Train l Analysis of Periodic Waveforms l Half-Range Expansion l Least Mean-Square Error Approximation l

Fourier Series Periodic Functions

The Mathematic Formulation l Any function that satisfies where T is a constant and is called the period of the function.

Example: Find its period. Fact: smallest T

Example: Find its period. must be a rational number

Example: Is this function a periodic one? not a rational number

Fourier Series

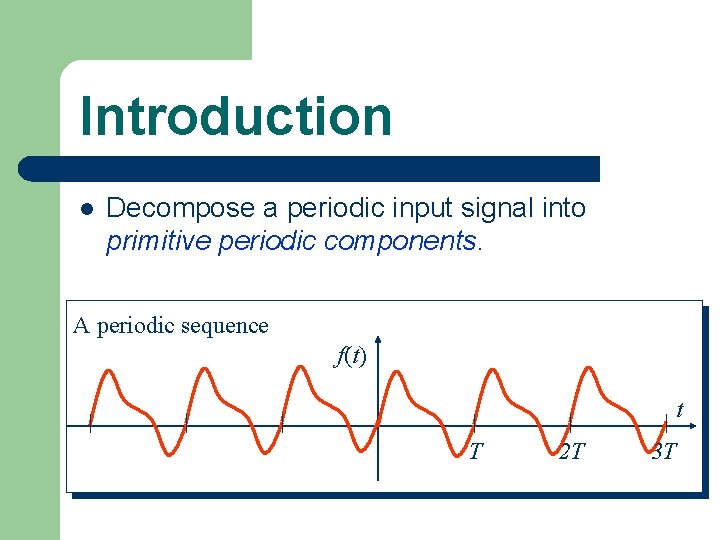
Introduction l Decompose a periodic input signal into primitive periodic components. A periodic sequence f(t) t T 2 T 3 T

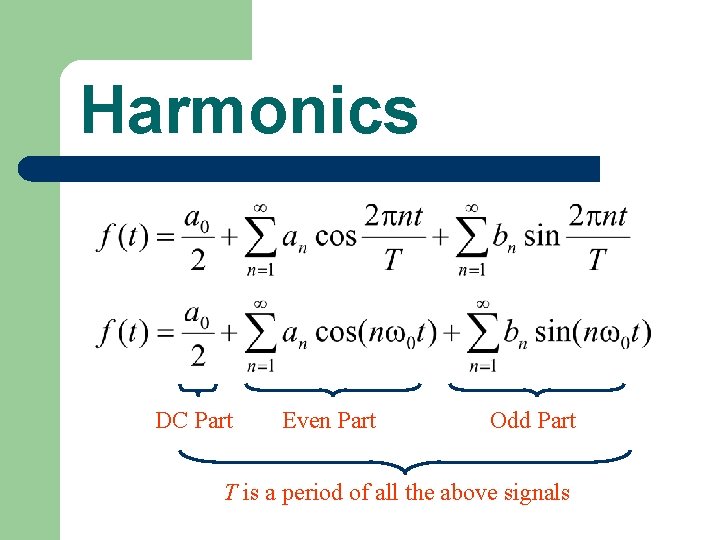
Synthesis DC Part Even Part Odd Part T is a period of all the above signals Let 0=2 /T.

Orthogonal Functions l Call a set of functions { k} orthogonal on an interval a < t < b if it satisfies

Orthogonal set of Sinusoidal Functions Define 0=2 /T. We now prove this one

Proof m n 0 0

Proof m=n 0

Orthogonal set of Sinusoidal Functions Define 0=2 /T. an orthogonal set.

Decomposition

Proof Use the following facts:

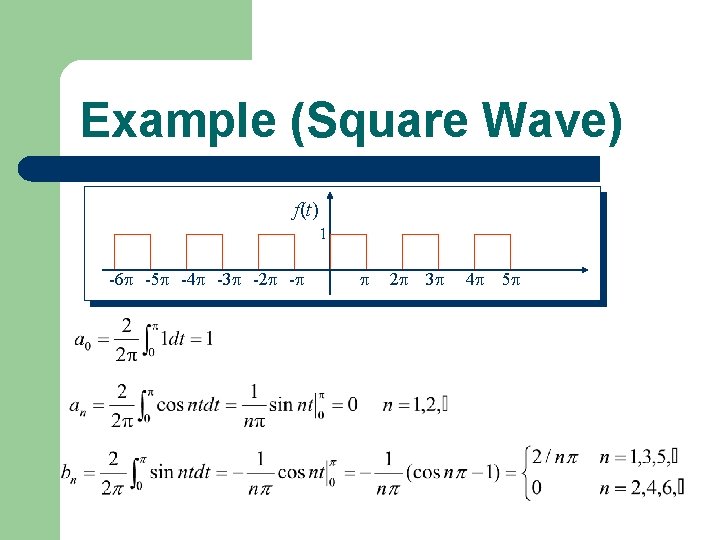
Example (Square Wave) f(t) 1 -6 -5 -4 -3 -2 - 2 3 4 5

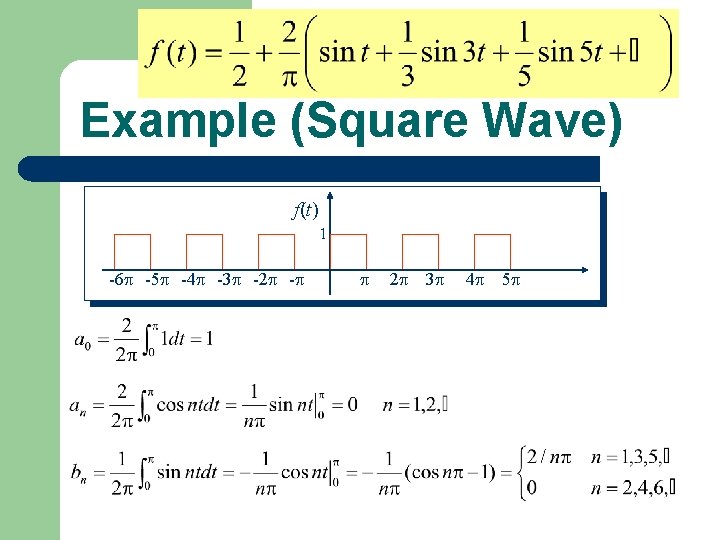
Example (Square Wave) f(t) 1 -6 -5 -4 -3 -2 - 2 3 4 5

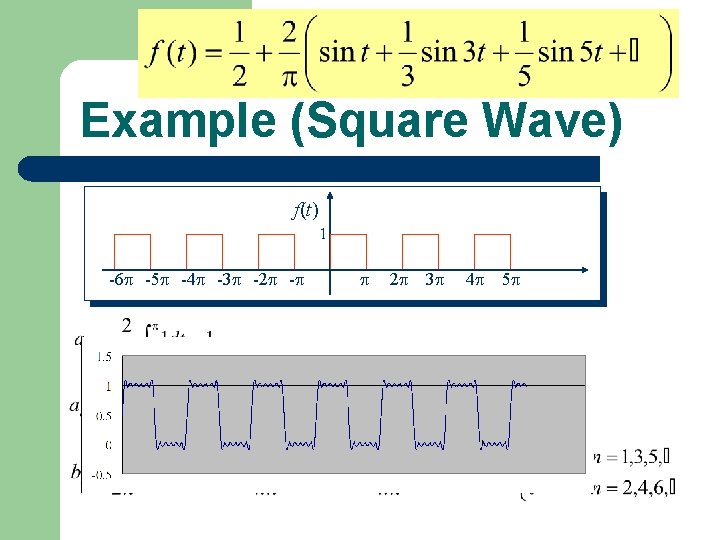
Example (Square Wave) f(t) 1 -6 -5 -4 -3 -2 - 2 3 4 5

Harmonics DC Part Even Part Odd Part T is a period of all the above signals

Harmonics Define , called the fundamental angular frequency. Define , called the n-th harmonic of the periodic function.

Harmonics

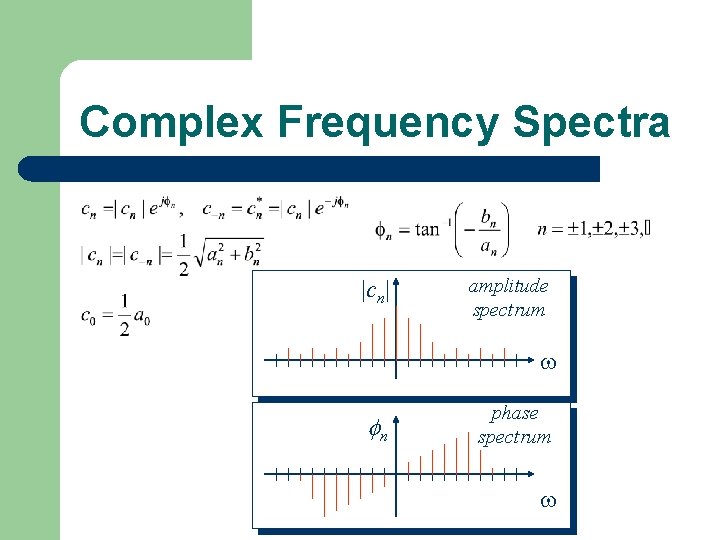
Amplitudes and Phase Angles harmonic amplitude phase angle

Fourier Series Complex Form of the Fourier Series

Complex Exponentials

Complex Form of the Fourier Series

Complex Form of the Fourier Series

Complex Form of the Fourier Series

Complex Form of the Fourier Series If f(t) is real,

Complex Frequency Spectra |cn| amplitude spectrum n phase spectrum

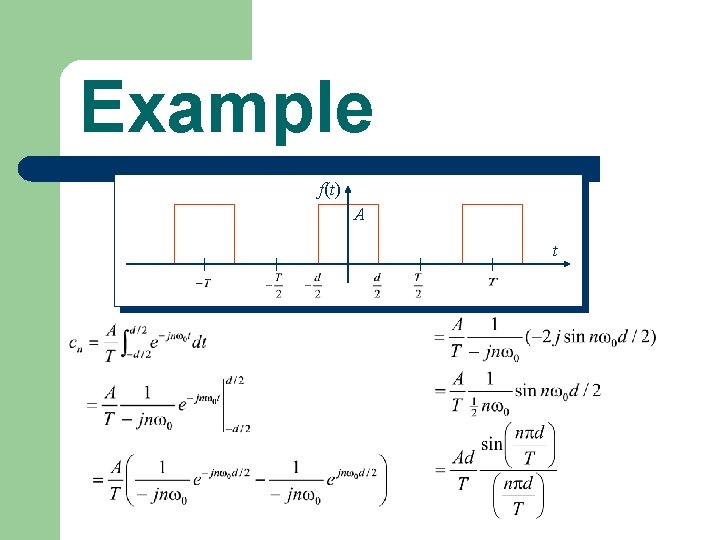
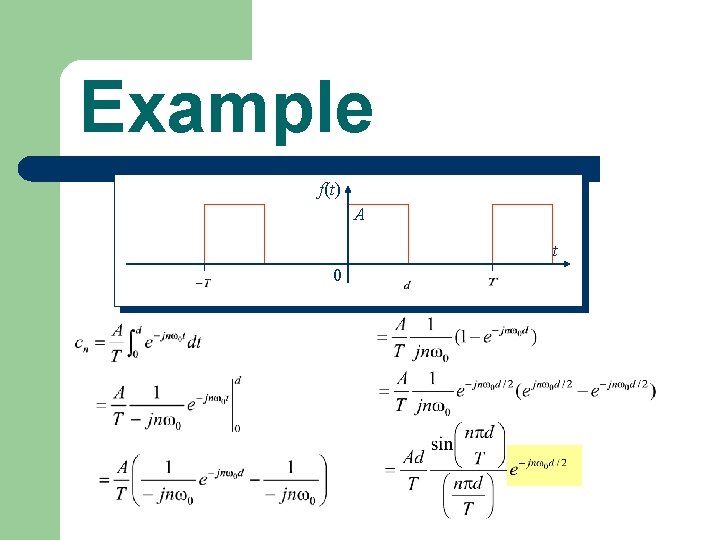
Example f(t) A t

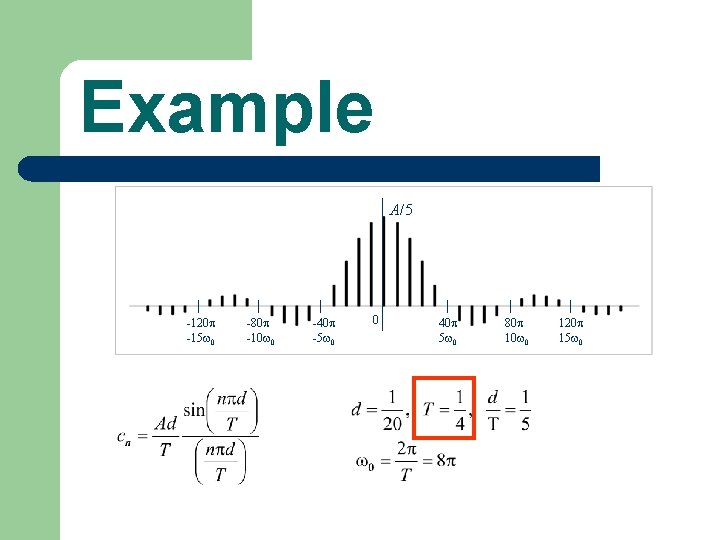
Example A/5 -120 -15 0 -80 -10 0 -40 -5 0 0 40 5 0 80 10 0 120 15 0

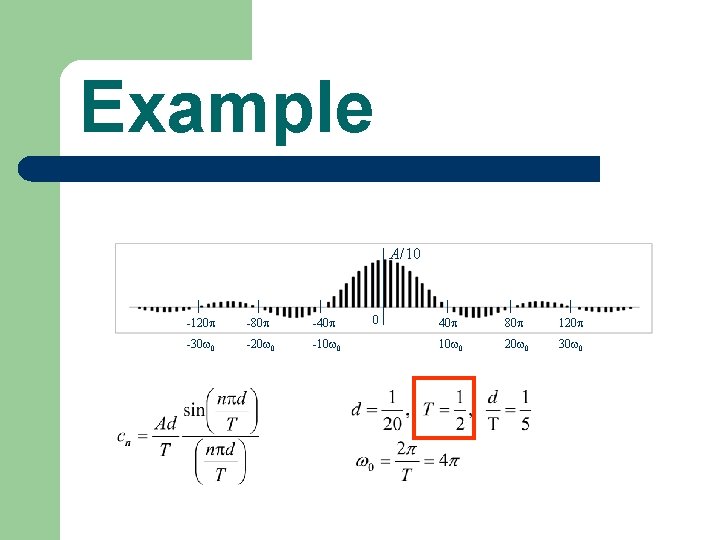
Example A/10 -120 -80 -40 -30 0 -20 0 -10 0 0 40 80 120 10 0 20 0 30 0

Example f(t) A t 0

Fourier Series Impulse Train

Dirac Delta Function and Also called unit impulse function. 0 t

Property (t): Test Function

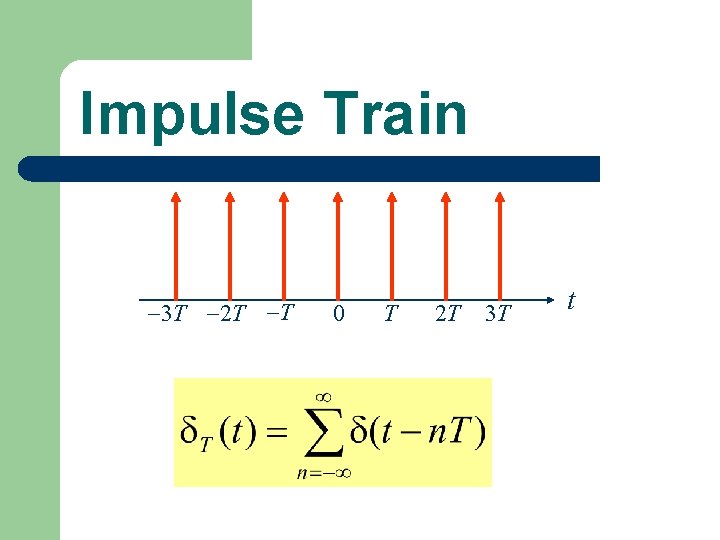
Impulse Train 3 T 2 T T 0 T 2 T 3 T t

Fourier Series of the Impulse Train

Complex Form Fourier Series of the Impulse Train

Fourier Series Analysis of Periodic Waveforms

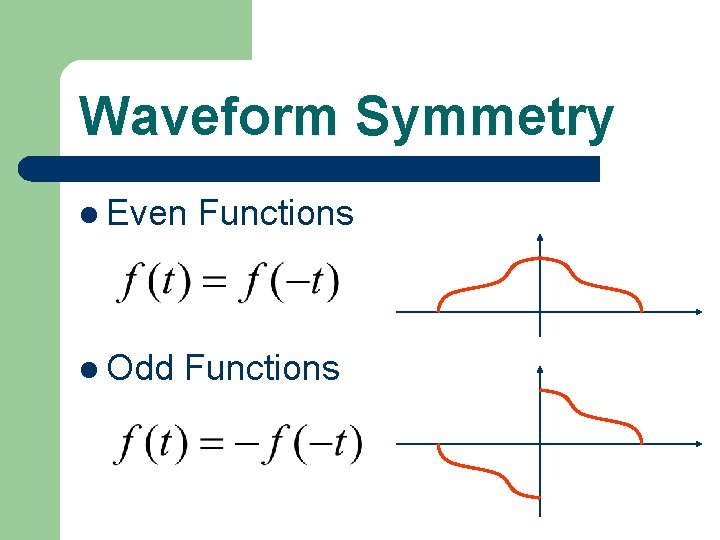
Waveform Symmetry l Even l Odd Functions

Decomposition l Any function f(t) can be expressed as the sum of an even function fe(t) and an odd function fo(t). Even Part Odd Part

Example Even Part Odd Part
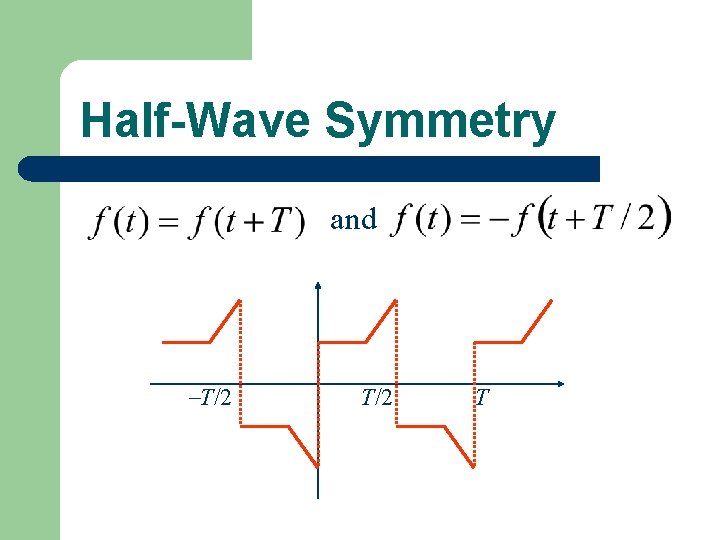
Half-Wave Symmetry and T/2 T

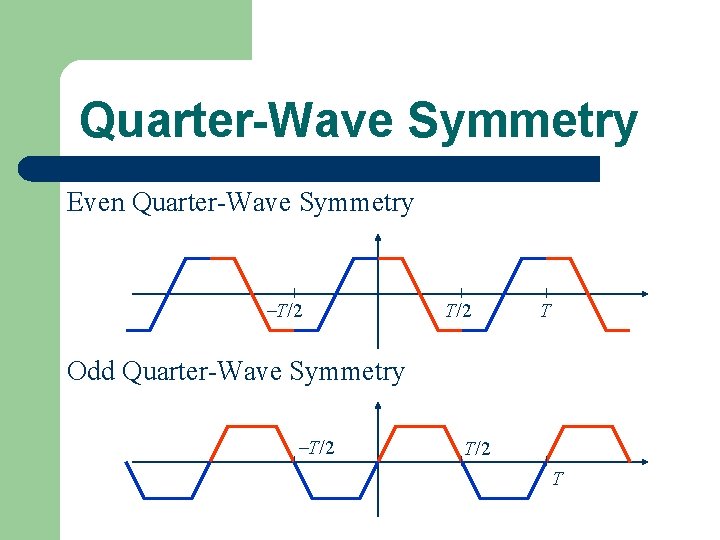
Quarter-Wave Symmetry Even Quarter-Wave Symmetry T/2 T Odd Quarter-Wave Symmetry T/2 T

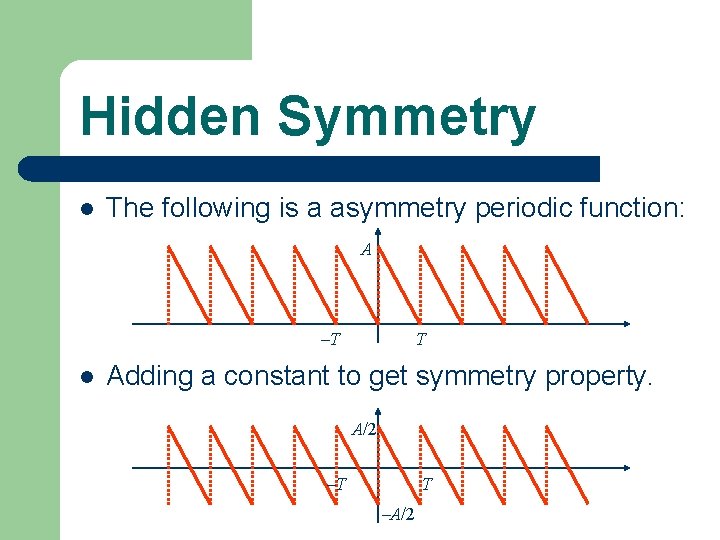
Hidden Symmetry l The following is a asymmetry periodic function: A T l T Adding a constant to get symmetry property. A/2 T T A/2

Fourier Coefficients of Symmetrical Waveforms l The use of symmetry properties simplifies the calculation of Fourier coefficients. – – – Even Functions Odd Functions Half-Wave Even Quarter-Wave Odd Quarter-Wave Hidden

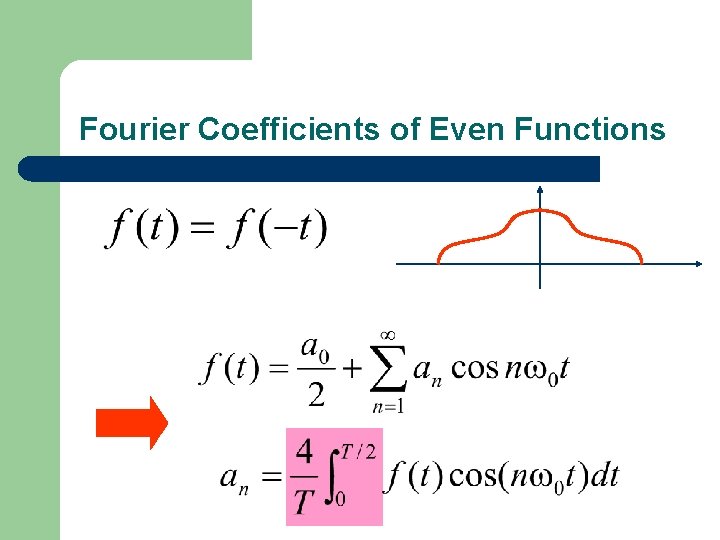
Fourier Coefficients of Even Functions

Fourier Coefficients of Even Functions

Fourier Coefficients for Half-Wave Symmetry and T/2 T The Fourier series contains only odd harmonics.

Fourier Coefficients for Half-Wave Symmetry and

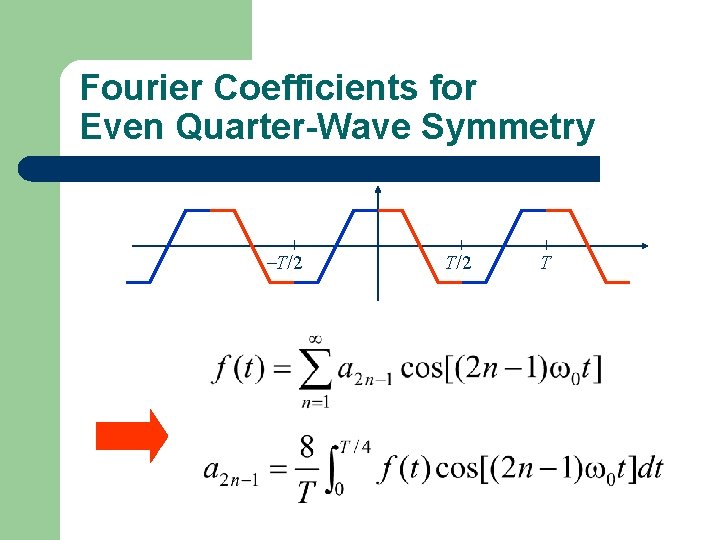
Fourier Coefficients for Even Quarter-Wave Symmetry T/2 T

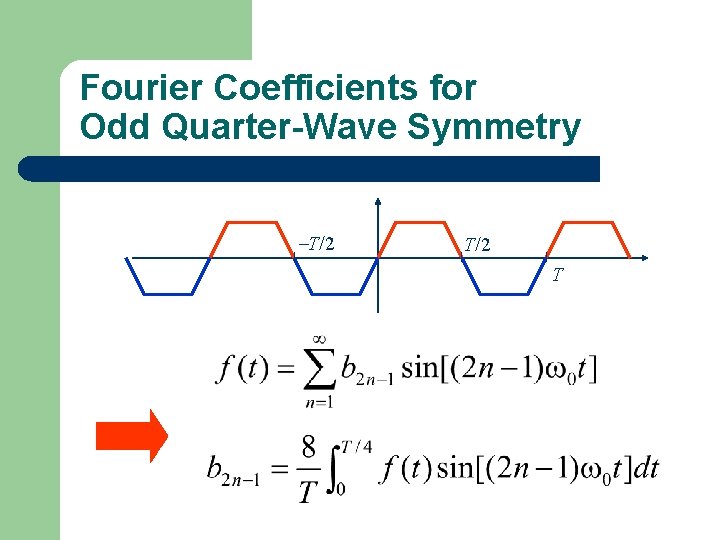
Fourier Coefficients for Odd Quarter-Wave Symmetry T/2 T

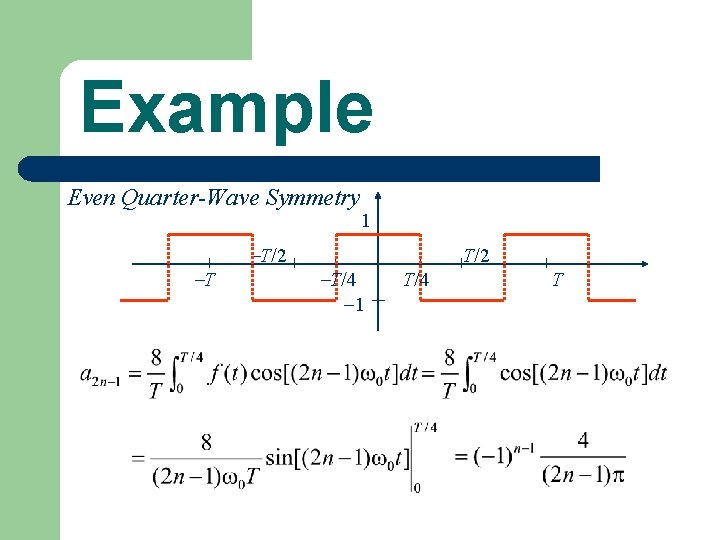
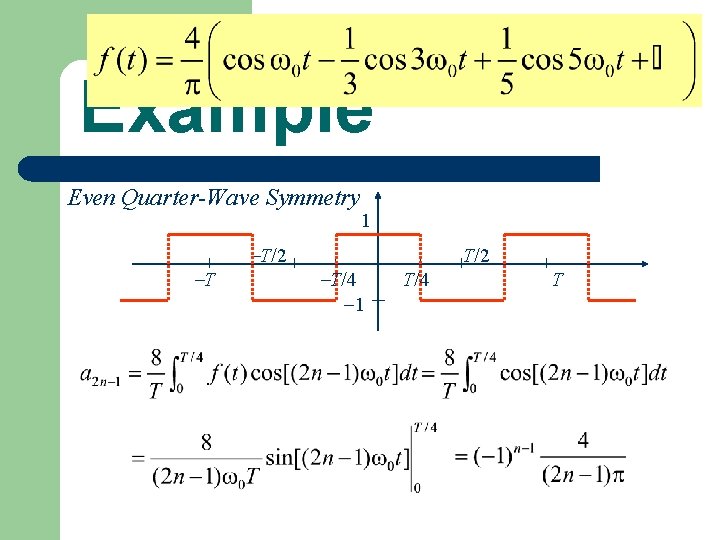
Example Even Quarter-Wave Symmetry T T/2 T/4 1 1 T/2 T/4 T

Example Even Quarter-Wave Symmetry T T/2 T/4 1 1 T/2 T/4 T

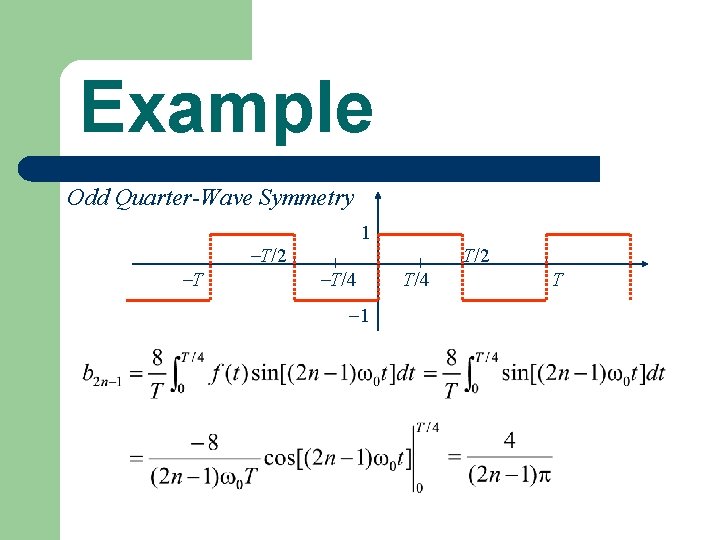
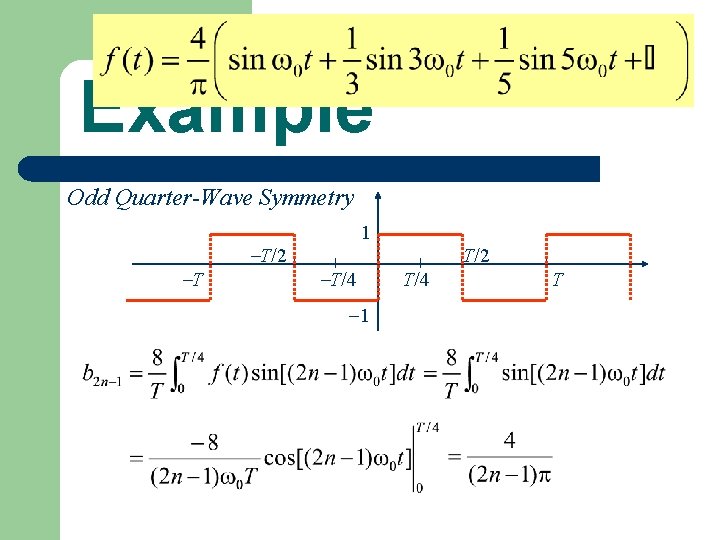
Example Odd Quarter-Wave Symmetry T T/2 1 T/4 1 T/2 T/4 T

Example Odd Quarter-Wave Symmetry T T/2 1 T/4 1 T/2 T/4 T

Fourier Series Half-Range Expansions

Non-Periodic Function Representation l A non-periodic function f(t) defined over (0, ) can be expanded into a Fourier series which is defined only in the interval (0, ).

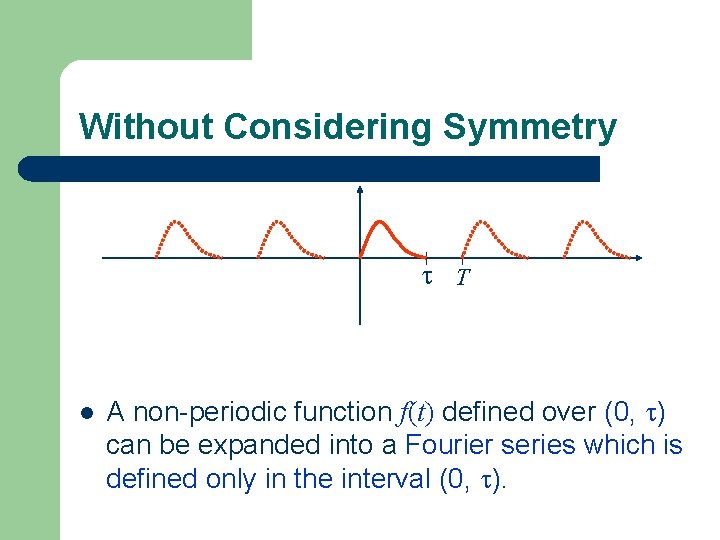
Without Considering Symmetry T l A non-periodic function f(t) defined over (0, ) can be expanded into a Fourier series which is defined only in the interval (0, ).

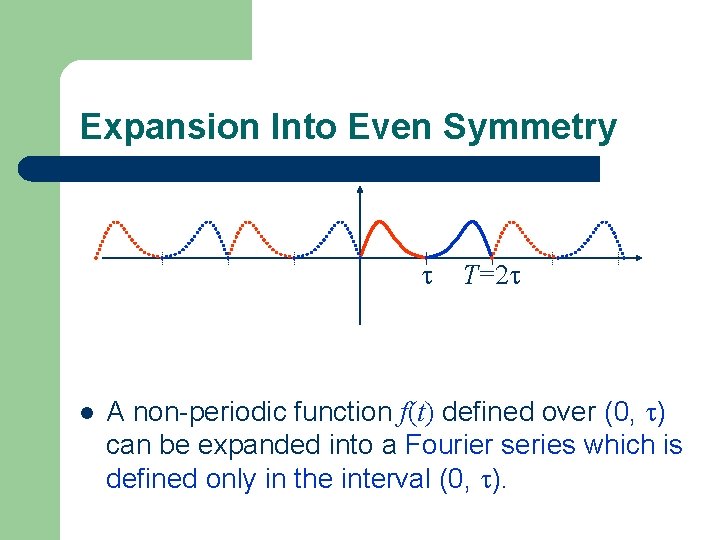
Expansion Into Even Symmetry l T=2 A non-periodic function f(t) defined over (0, ) can be expanded into a Fourier series which is defined only in the interval (0, ).

Expansion Into Odd Symmetry T=2 l A non-periodic function f(t) defined over (0, ) can be expanded into a Fourier series which is defined only in the interval (0, ).

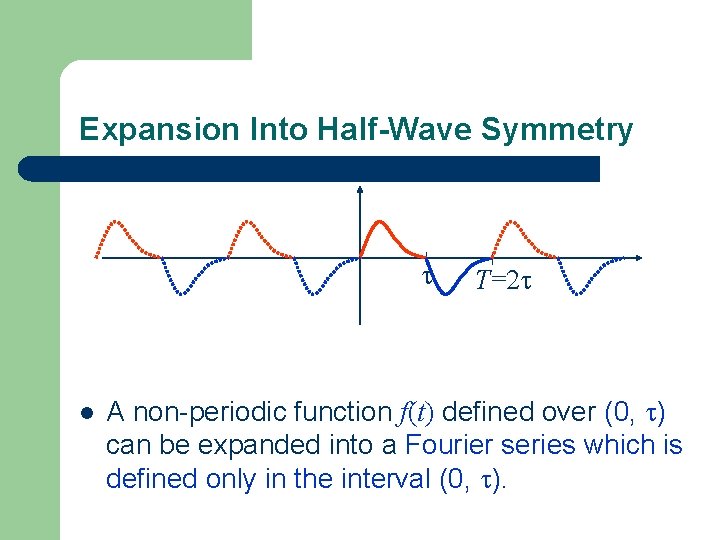
Expansion Into Half-Wave Symmetry l T=2 A non-periodic function f(t) defined over (0, ) can be expanded into a Fourier series which is defined only in the interval (0, ).

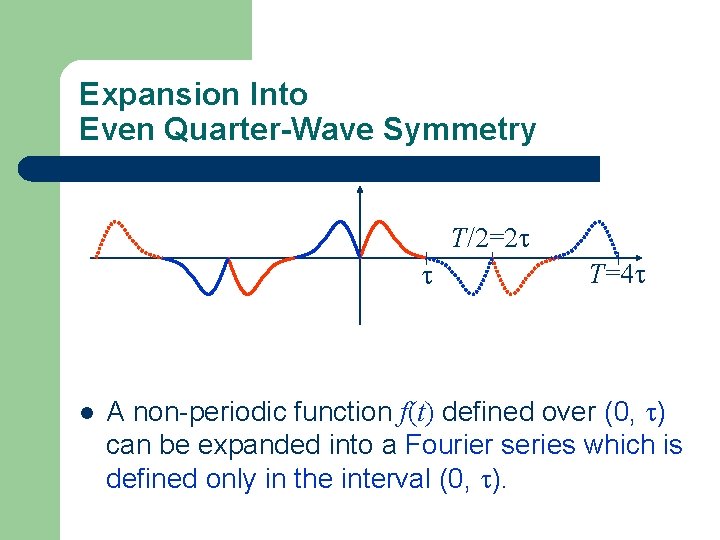
Expansion Into Even Quarter-Wave Symmetry T/2=2 l T=4 A non-periodic function f(t) defined over (0, ) can be expanded into a Fourier series which is defined only in the interval (0, ).

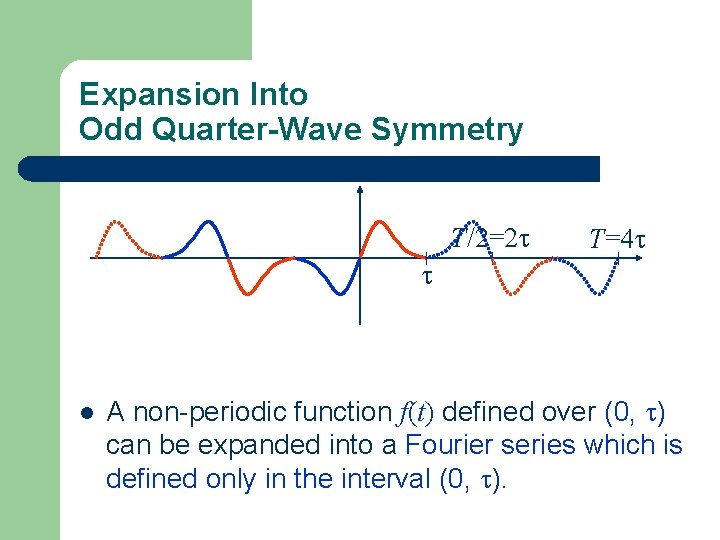
Expansion Into Odd Quarter-Wave Symmetry T/2=2 T=4 l A non-periodic function f(t) defined over (0, ) can be expanded into a Fourier series which is defined only in the interval (0, ).

Fourier Series Least Mean-Square Error Approximation

Approximation a function Use to represent f(t) on interval T/2 < t < T/2. Define Mean-Square Error

Approximation a function Show that using Sk(t) to represent f(t) has least mean-square property. Proven by setting Ek/ ai = 0 and Ek/ bi = 0.

Approximation a function

Mean-Square Error

Mean-Square Error

Mean-Square Error