Foundations of Cryptography Lecture 8 Application of GL

Foundations of Cryptography Lecture 8: Application of GL, Next-bit unpredictability, Pseudo-Random Functions. Lecturer: Moni Naor

Recap of last week’s lecture • Hardcore Predicates and Pseudo-Random Generators • Inner product is a hardcore predicate for all functions – Proof via list decoding – Interpretations – Applications to Diffie-Hellman

Inner Product Hardcore bit • The inner product bit: choose r R {0, 1}n let h(x, r) = r ∙x = ∑ xi ri mod 2 Theorem [Goldreich-Levin]: for any one-way function the inner product is a hardcore predicate Proof structure: Algorithm A’ for inverting f 1. There are many x’s for which A returns a correct answer (r ∙x) on ½+ε of the r ’s 2. Reconstruction algorithm R: take an algorithm A that guesses h(x, r) correctly with probability ½+ε over the r‘s and output a list of candidates for x – No use of the y info by R (except feeding to A) 3. Choose from the list the/an x such that f(x)=y The main step!

Application: if subset is one-way, then it is a pseudo-random generator • Subset sum problem: given – n numbers 0 ≤ a 1, a 2 , …, an ≤ 2 m – Target sum y – Find subset S⊆ {1, . . . , n} ∑ i S ai, =y • Subset sum one-way function f: {0, 1}mn+n → {0, 1}m+mn f(a 1, a 2 , …, an , x 1, x 2 , …, xn ) = (a 1, a 2 , …, an , ∑ i=1 n xi ai mod 2 m ) If m<n then we get out less bits then we put in. If m>n then we get out more bits then we put in. Theorem: if for m>n subset sum is a one-way function, then it is also a pseudo-random generator.

Subset Sum Generator Idea of proof: use the distinguisher A to compute r ∙x For simplicity: do the computation mod P for large prime P Given r {0, 1}n and (a 1, a 2 , …, an , y) Generate new problem (a’ 1, a’ 2 , …, a’n , y’): Prob[A=‘ 0’|pseudo]= ½+ε • Choose c R ZP Prob[A=‘ 0’|random]= ½ • Let a’i = ai if ri=0 and ai =ai+c mod P if ri=1 • Guess k R {0, , n} - the value of ∑ xi ri – the number of locations where x and r are 1 Pseudo • Let y’ = y+c k mod P Run the distinguisher A on (a’ 1, a’ 2 , …, a’n , y’)random – output what A says Xored with parity(k) Claim: if k is correct, then (a’ 1, a’ 2 , …, a’n , y’) is R pseudorandom Claim: for any incorrect k: (a’ 1, a’ 2 , …, a’n , y’) is R random y’= z + (k-h)c modk. P where z = ∑ correct i=1 n xi a’i mod P and h=∑ xi ri Incorrect k Therefore: probability Probability over a 1, a 2 to , …, guess an, x andrr∙x andis 1/n∙(½+ε) + (n-1)/n (½)= ½+ε/n

Interpretations of the Goldreich-Levin Theorem • A tool for constructing pseudo-random generators The main part of the proof: • A mechanism for translating `general confusion’ into randomness – Diffie-Hellman example • List decoding of Hadamard Codes – works in the other direction as well (for any code with good list decoding) – List decoding, as opposed to unique decoding, allows getting much closer to distance • `Explains’ unique decoding when prediction was 3/4+ε • Finding all linear functions agreeing with a function given in a black-box – Learning all Fourier coefficients larger than ε • If the Fourier coefficients are concentrated on a small set – can find them – True for AC 0 circuits

Two important techniques for showing pseudo-randomness • Hybrid argument • Next-bit prediction and pseudorandomness

Hybrid argument To prove that two distributions D and D’ are indistinguishable: • suggest a collection of distributions D= D 0, D 1, … Dk =D’ If D and D’ can be distinguished, then there is a pair Di and Di+1 that can be distinguished. Advantage ε in distinguishing between D and D’ means advantage ε/k between some Di and Di+1 Use a distinguisher for the pair Di and Di+1 to derive a contradiction

Composing PRGs Composition Let • g 1 be a (ℓ 1, ℓ 2 )-pseudo-random generator • g 2 be a (ℓ 2, ℓ 3)-pseudo-random generator Consider g(x) = g 2(g 1(x)) Claim: g is a (ℓ 1, ℓ 3 )-pseudo-random generator ℓ Proof: consider three distributions on {0, 1} 3 ℓ 1 ℓ 2 ℓ 3 – D 1: y uniform in {0, 1}ℓ 3 ℓ – D 2: y=g(x) for x uniform in {0, 1} 1 – D 3: y=g 2(z) for z uniform in {0, 1}ℓ 2 By assumption there is a distinguisher A between D 1 and D 2 A must either or Distinguish between D 1 and D 3 - can use A use to distinguish g 2 Distinguish between D 2 and D 3 triangle inequality - can use A use to distinguish g 1

Composing PRGs When composing • a generator secure against advantage ε 1 and a • a generator secure against advantage ε 2 we get security against advantage ε 1+ε 2 When composing the single bit expansion generator m times Loss in security is at most ε/m Hybrid argument: to prove that two distributions D and D’ are indistinguishable: suggest a collection of distributions D= D 0, D 1, … Dk =D’ such that If D and D’ can be distinguished, there is a pair Di and Di+1 that can be distinguished. Difference ε between D and D’ means ε/k between some Di and Di+1 Use such a distinguisher to derive a contradiction

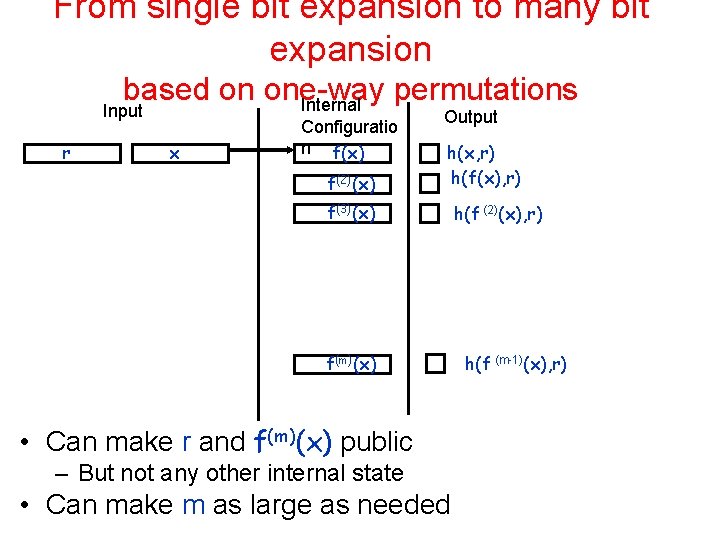
From single bit expansion to many bit expansion based on one-way permutations Internal Input r x Configuratio n f(x) f(2)(x) Output h(x, r) h(f(x), r) f(3)(x) f(m)(x) • Can make r and f(m)(x) public – But not any other internal state • Can make m as large as needed h(f (2)(x), r) h(f (m-1)(x), r)

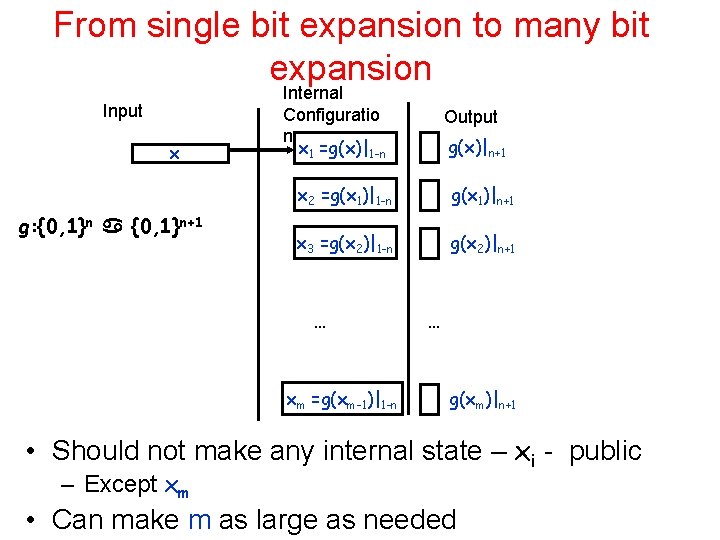
From single bit expansion to many bit expansion Input x g: {0, 1}n+1 Internal Configuratio n x 1 =g(x)|1 -n Output g(x)|n+1 x 2 =g(x 1)|1 -n g(x 1)|n+1 x 3 =g(x 2)|1 -n g(x 2)|n+1 … xm =g(xm-1)|1 -n … g(xm)|n+1 • Should not make any internal state – xi - public – Except xm • Can make m as large as needed

Exercise • Let {Dn} and {D’n} be two distributions that are – Computationally indistinguishable – Polynomial time samplable • Suppose that {y 1, … ym} are all sampled according to {Dn} or all are sampled according to {D’n} • Prove: no probabilistic polynomial time machine can tell, given {y 1, … ym}, whether they were sampled from {Dn} or {D’n}

Existence of PRGs What we have proved: Theorem: if pseudo-random generators stretching by a single bit exist, then pseudo-random generators stretching by any polynomial factor exist Theorem: if one-way permutations exist, then pseudo-random generators exist A much harder theorem to prove: Theorem [HILL]: if one-way functions exist, then pseudo-random generators exist

Two important techniques for showing pseudo-randomness • Hybrid argument • Next-bit prediction and pseudorandomness

Next-bit Test Definition: a function g: {0, 1}* → {0, 1}* is next-bit unpredictable if: • It is polynomial time computable • It stretches the input |g(x)|>|x| – denote by ℓ(n) the length of the output on inputs of length n • If the input (seed) is random, then the output passes the next -bit test For any prefix 0≤ i< ℓ(n), for any PPT adversary A that is a predictor: receives the first i bits of y= g(x) and tries to guess the next bit, for any polynomial p(n) and sufficiently large n |Prob[A(yi, y 2, …, yi) = yi+1] – 1/2 | < 1/p(n) Theorem: a function g: {0, 1}* → {0, 1}* is next-bit unpredictable if

Proof of equivalence • If g is a presumed pseudo-random generator and there is a predictor for the next bit: can use it to distinguish Distinguisher: – If predictor is correct: guess ‘pseudo-random’ – If predictor is not-correct: guess ‘random’ • On outputs of g distinguisher is correct with probability at least 1/2 + 1/p(n) • On uniformly random inputs distinguisher is correct with probability exactly 1/2

…Proof of equivalence • If there is distinguisher A for the output of g from random: form a sequence of distributions and use the successes of A to predict the next bit for some value Dℓ g(x)=y 1, y 2 yℓ r 1, r 2 r ℓ 2 R U ℓ y 1, y 2 yℓ-1 yℓ y 1, y 2 yℓ-1 rℓ y 1, y 2 yi ri+1 rℓ r 1, r 2 rℓ-1 rℓ Dℓ-1 Di D 0 There exists an 0 · i · ℓ-1 where A can distinguish Di from

Next-block Undpredictable Suppose that g maps a given a seed S into a sequence of blocks g S y 1 y 2, … , let ℓ(n) be the number of blocks given a seed of length n • Passes the next-block unpredicatability test For any prefix 0 ≤ i< ℓ(n), for any probabilistic polynomial time adversary A that receives the first i blocks of y= g(x) and tries to guess the next block yi+1, for any polynomial p(n) and sufficiently large n |Prob[A(y 1, y 2, …, yi)= yi+1] | < 1/p(n)

Pseudo-random Generators and Encryption Output of a pseudorandom generator A pseudo-random string should be able to replace any random string • When running an algorithm – If the results are measurably different, can use as distinguisher – Basis of derandomization • For encrypting communication: as one-time pad – Need to define the type of desired protection of messages • Semantic Security • Indistinguishability of encryption Uniformit y

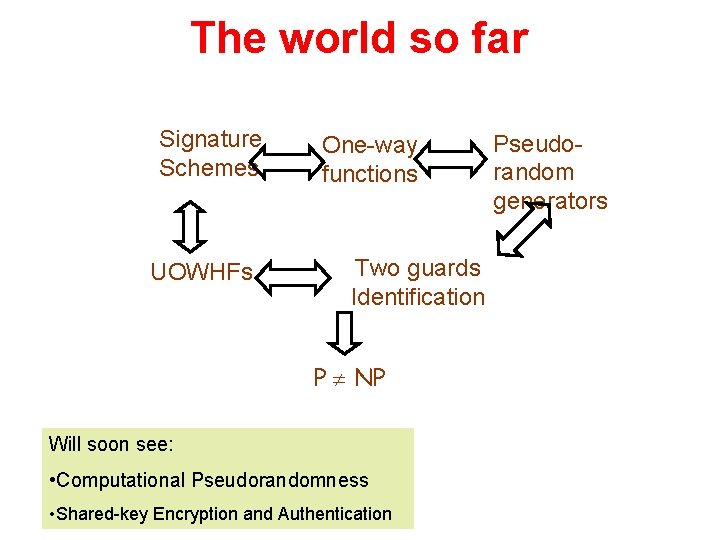
The world so far Signature Schemes UOWHFs One-way functions Two guards Identification P NP Will soon see: • Computational Pseudorandomness • Shared-key Encryption and Authentication Pseudorandom generators

Pseudo-Random Generators concrete version Gn: 0, 1 m 0, 1 n Instead of passes all polynomial time statistical tests: (t, )-pseudo-random - no test A running in time t can distinguish with advantage

Recall: Three Basic issues in cryptography • Identification • Authentication • Encryption Solve in a shared key environment A B S S

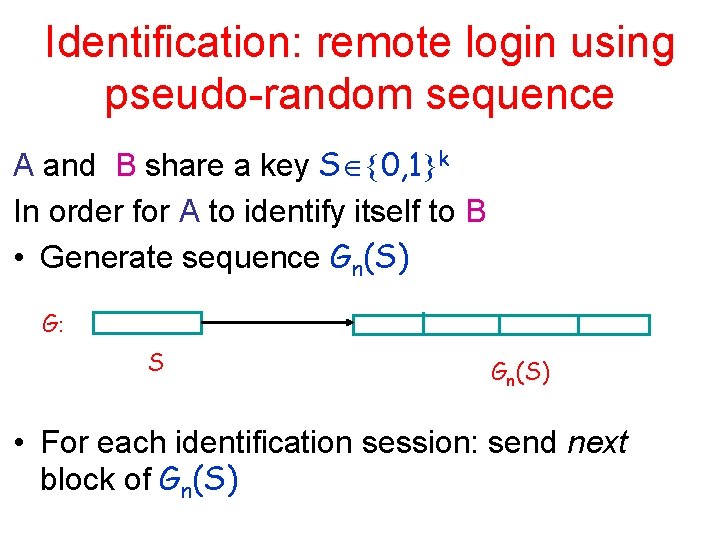
Identification: remote login using pseudo-random sequence A and B share a key S 0, 1 k In order for A to identify itself to B • Generate sequence Gn(S) G: S Gn(S) • For each identification session: send next block of Gn(S)

Problems. . . • • More than two parties Malicious adversaries - add noise Coordinating the location block number Better approach: Challenge-Response

Challenge-Response Protocol • B selects a random location and sends to A • A sends value at random location A B What’s this?

Desired Properties • Very long string - prevent repetitions • Random access to the sequence • Unpredictability - cannot guess the value at a random location – even after seeing values at many parts of the string to the adversary’s choice. – Pseudo-randomness implies unpredictability • Not the other way around for blocks

Authenticating Messages • A wants to send message M 0, 1 n to B • B should be confident that A is indeed the sender of M One-time application: S =(a, b): where a, b R 0, 1 n To authenticate M: supply a. M b Computation is done in GF[2 n]

Problems and Solutions • Problems - same as for identification • If a very long random string available – can use for one-time authentication – Works even if only random looking a, b A B Use this!

Encryption of Messages • A wants to send message M 0, 1 n to B • only B should be able to learn M One-time application: S = a: where a R 0, 1 n To encrypt M send a M

Encryption of Messages • If a very long random looking string available – can use as in one-time encryption A B Use this!

Pseudo-random Function • A way to provide an extremely long shared string

Pseudo-random Functions Concrete Treatment: F: 0, 1 k 0, 1 n 0, 1 m key Domain Range Denote Y= FS (X) A family of functions Φk ={FS | S 0, 1 k is (t, , q)-pseudo-random if it is • Efficiently computable - random access and. . .

(t, , q)-pseudo-random The tester A that can choose adaptively – X 1 and gets Y 1= FS (X 1) – X 2 and gets Y 2 = FS (X 2 ) … – Xq and gets Yq= FS (Xq) • Then A has to decide whether – FS R Φk or – FS R R n m = F | F : 0, 1 n 0, 1 m

(t, , q)-pseudo-random For a function F chosen at random from (1) Φk ={FS | S 0, 1 k (2) R n m = F | F : 0, 1 n 0, 1 m For all t-time machines A that choose q locations and try to distinguish (1) from (2) Prob A ‘ 1’ F R Fk - Prob A ‘ 1’ F R R n m

Equivalent/Non-Equivalent Definitions • Instead of next bit test: for X X 1, X 2 , , Xq chosen by A, decide whether given Y is – Y= FS (X) or – Y R 0, 1 m • Adaptive vs. Non-adaptive • Unpredictability vs. pseudo-randomness • A pseudo-random sequence generator g: 0, 1 m 0, 1 n – a pseudo-random function on small domain 0, 1 log n 0, 1 with key in 0, 1 m

Application to the basic issues in cryptography Solution using a shared key S Identification: B to A: X R 0, 1 n A to B: Y= FS (X) A verifies Authentication: A to B: Y= FS (M) replay attack Encryption: A chooses X R 0, 1 n A to B: <X , Y= FS (X) M >

Reading Assignment • Naor and Reingold, From Unpredictability to Indistinguishability: A Simple Construction of Pseudo-Random Functions from MACs, Crypto'98. www. wisdom. weizmann. ac. il/~naor/PAPERS/mac_abs. html • Gradwohl, Naor, Pinkas and Rothblum, Cryptographic and Physical Zero-Knowledge Proof Systems for Solutions of Sudoku Puzzles – Especially Section 1 -3 www. wisdom. weizmann. ac. il/~naor/PAPERS/sudoku_abs. ht ml

Sources • Goldreich’s Foundations of Cryptography, volumes 1 and 2 • M. Blum and S. Micali, How to Generate Cryptographically Strong Sequences of Pseudo-Random Bits , SIAM J. on Computing, 1984. • O. Goldreich and L. Levin, A Hard-Core Predicate for all One-Way Functions, STOC 1989. • Goldreich, Goldwasser and Micali, How to construct random functions , Journal of the ACM