Foundations of Classical Electrodynamics and Optical Experiments to

Foundations of Classical Electrodynamics and Optical Experiments to Measure the Parameters of the PPM (Parametrized Post-Maxewellian) Electrodynamics 經典電動力學的基礎(ar. Xiv 1109. 5501) W. -T. Ni 倪維斗 Department of Physics, National Tsing Hua University weitou@gmail. com 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 1

Outline n n n n n Introduction – Maxwell equations and Lorentz force law Photon mass constraints Quantum corrections – quantum corrections Parametrized Post-Maxwell (PPM) electrodynamics Electromagnetic wave propagation Measuring the parameters of the PPM electrodynamics Electrodynamics in curved spacetime and EEP Empirical tests of electromagnetism and the χ-g framework Pseudoscalar-photon interaction and the cosmic pol. rotation Discussion and outlook 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 2

Introduction – Maxwell Equations and Lorentz Force Law (I) 馬克士威方程式與羅倫茲力 (Jackson) (法拉第定律) (無磁單極) (庫倫定律) (安培-馬克士威定律) 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 3

Introduction – Maxwell Equations and Lorentz Force Law (II) 馬克士威方程式與羅倫茲力 (連續方程式-電荷守恆) (羅倫茲力) n Charges (and currents) produce E and B fields influence the Motion of charges Maxwell Equations Lorentz Force Law 電荷和電流產生電場和磁場；電場和磁場影響電荷的運動 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 4

Introduction – Maxwell Equations and Lorentz Force Law (III) 馬克士威方程式與羅倫茲力 n n n 法拉第定律和無磁單極定律相當於電場和磁場可以由 標量勢 和向量勢A表示： 4 -vector potential A ( , A) Second-rank, antisymmetric field-strength tensor F = ∂ A - ∂ A Electric field E [≡ (E 1, E 2, E 3) ≡ (F 01, F 02, F 03)] and magnetic induction B [≡ (B 1, B 2, B 3) ≡ (F 32, F 13, F 21)] Electromagnetic field Lagrangian density LEM = (1/8π)[E 2 -B 2]. 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 5

Lagrangian density LEMS for a system of charged particles in Gaussian units n n n 2011. 12. NTHU LEMS=LEM+LEM-P+LP =-(1/(16π))[(1/2)ηikηjl-(1/2)ηilηkj]Fij. Fkl -Akjk-ΣI m. I[(ds. I)/(dt)]δ(x-x. I), LEMS 整个電荷系統拉格朗日 LEM 電磁場拉格朗日 LEM-P 電磁場-粒子相互作用拉格朗日 LP 粒子拉格朗日 Foundations of Classical Electrodynamics and PPM Framework W-T Ni 6

Test of Coulomb’s Law 1/r 2+ n n Cavendish 1772 | | 0. 02 4 MHz 10 k. V p Maxwell 1879 | | 5 10 -5 Plimpton and Lawton | | 2 10 -9 Williams, Faller, and Hill 1971 = (2. 7 3. 1) 10 -16 2011. 12. NTHU 1. 5 m 12. 1 in Foundations of Classical Electrodynamics and PPM Framework W-T Ni 7

Proca (1936 -8) Lagrangian density and mass of photon n 2011. 12. NTHU LProca = (mphoton 2 c 2/8πħ 2)(Ak. Ak) the Coulomb law is modified to have the electric potential A 0 = q(e-μr/r) where q is the charge of the source particle, r is the distance to the source particle, and μ (≡mphotonc/ħ) gives the inverse range of the interaction Foundations of Classical Electrodynamics and PPM Framework W-T Ni 8

Constraints on the mass of photon Williams, Faller & Hill mphoton ≤ 10 -14 e. V (1971) Lab Test (= 2 × 10 -47 g) μ-1 ≥ 2 × 107 m Davis, Goldhaber & Nieto (1975) Pioneer 10 Jupitor flyby mphoton ≤ 4 × 10 -16 e. V μ-1 ≥ 5 × 108 m Ryutov (2007) Solar wind magnetic field mphoton ≤ 10 -18 e. V μ-1 ≥ 2 × 1011 m Chibisov (1976) galactic sized fields mphoton ≤ 2 × 10 -27 e. V μ-1 ≥ 1020 m (= 7 × (= 2 × (= 4 × 10 -49 10 -51 10 -60 g) g) g) A good Reference: Goldhaber, A. S. & Nieto, M. M. (2010). Photon and Graviton Mass Limits. Review of Modern Physics, Vol. 82, No. 1, (January-March 2010), pp. 939 -979 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 9

Quantum corrections to classical electrodynamics Heisenberg-Euler Lagrangian 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 10

Born-Infeld Electrodynamics 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 11

Parametrized Post-Maxwell (PPM) Lagrangian density (4 parameters: ξ, η 1, η 2, η 3) n n n LPPM = (1/8π){(E 2 -B 2)+ξΦ(E∙B) +Bc-2[η 1(E 2 -B 2)2 +4η 2(E∙B)2+2η 3(E 2 -B 2)(E∙B)]} LPPM = (1/(32π)){-2 Fkl. Fkl -ξΦF*kl. Fkl +Bc-2 [η 1(Fkl. Fkl)2+η 2(F*kl. Fkl)2+η 3(Fkl. Fkl)(F*ij. Fij)]} (manifestly Lorentz invariant form) Dual electomagnetic field F*ij ≡ (1/2)eijkl Fkl 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 12

Unified theory of nonlinear electrodynamics and gravity A. Torres-Gomez, K. Krasnov, & C. Scarinci PRD 83, 025023 (2011) n n A class of unified theories of electromagnetism and gravity with Lagrangian of the BF type (F: Curvature of the connection 1 -form A ( ), with a potential for the B ( ) field (Lie-algebra valued 2 -form), the gauge group is U(2) (complexified). Given a choice of the potential function theory is a deformation of (complex) general relativity and electromagnetism. 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 13

Equations for nonlinear electrodynamics (1) 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 14

Equations for nonlinear electrodynamics (2) 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 15

Electromagnetic wave propagation in PPM electrodynamics 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 16

2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 17

2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 18

Birefringence or no Birefringnce 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 19

Measuring the parameters of the PPM electrodynamics n 2011. 12. NTHU Δn = n║ - n┴ = 4. 0 x 10 -24 (Bext/1 T)2 Foundations of Classical Electrodynamics and PPM Framework W-T Ni 20

Measuring the parameters of the PPM electrodynamics n n n Let’s choose z-axis to be in the propagation direction, x-axis in the Eext direction and y-axis in the Bext direction, i. e. , k = (0, 0, k), Eext = (E, 0, 0) and Bext = (0, B, 0). n± = 1 + (η 1+η 2)(E 2+B 2 -EB)Bc-2± [(η 1 -η 2)2(E 2+B 2 -EB)2+η 32(E 2 -B 2)]1/2 Bc-2. (i) E=B as in the strong microwave cavity, the indices of refraction for light is n± = 1 + (η 1+η 2)B 2 Bc-2±(η 1 -η 2)B 2 Bc-2, with birefringence Δn given by Δn = 2(η 1 -η 2)B 2 Bc-2; (ii) E=0, B≠ 0, the indices of refraction for light is n± = 1 + (η 1+η 2)B 2 Bc-2±[(η 1 -η 2)2+η 32]1/2 B 2 Bc-2, Δn = 2[(η 1 -η 2)2+η 32]1/2 B 2 Bc-2. 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 21

Measuring the parameters of the PPM electrodynamics 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 22

Lab Experiment: Principle of Experiment 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 23

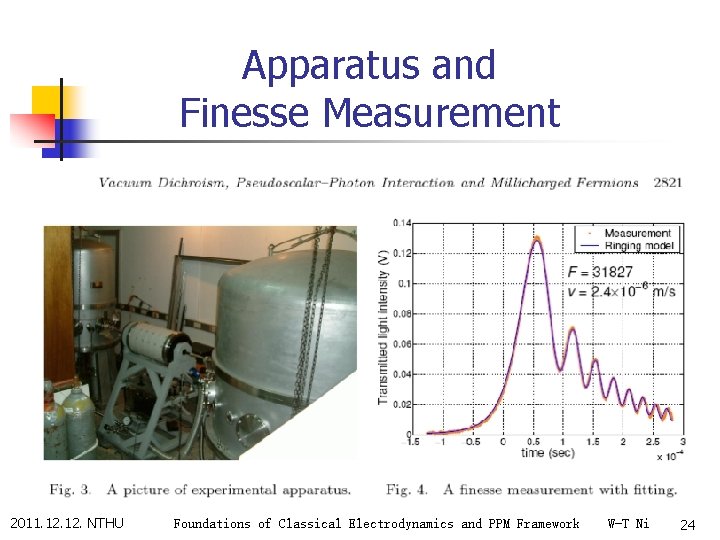
Apparatus and Finesse Measurement 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 24

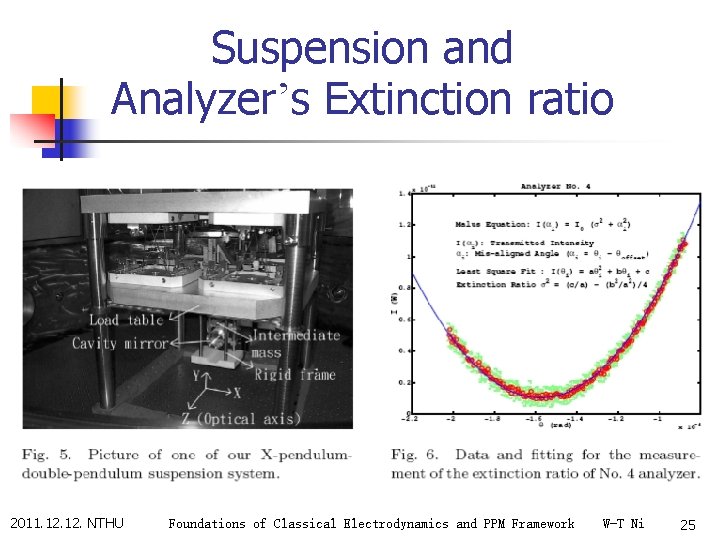
Suspension and Analyzer’s Extinction ratio 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 25

Injection Optical Bench 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T 26 Ni

2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 27

Vacuum Chamber and Magnet 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 28

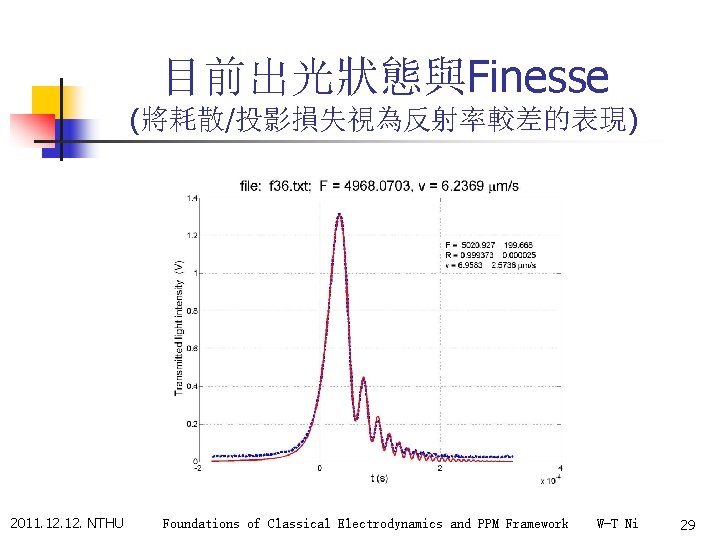
目前出光狀態與Finesse (將耗散/投影損失視為反射率較差的表現) 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 29

Current Optical Experiments LNL Ferrara 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 30

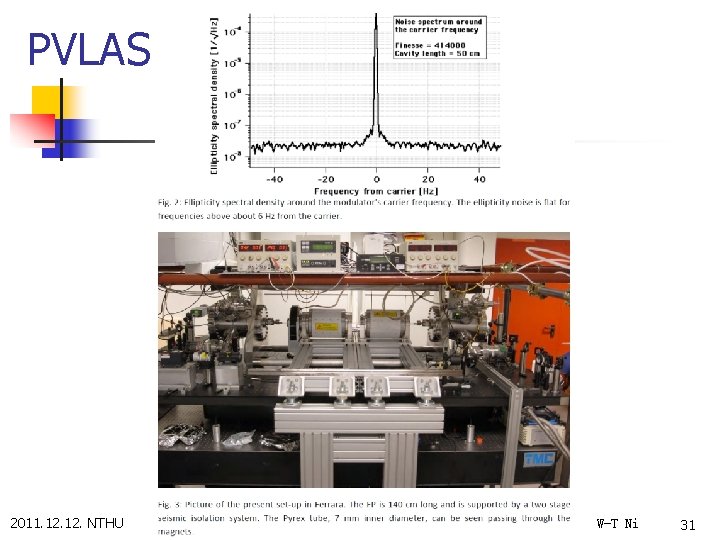
PVLAS 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 31

Rotation and ellipticity sensitivity comparisons using ellipsometers with optical path multipliers 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 32

PVLAS Ferrara on 3 competing experiments (I) n n Q & A in Taiwan: They have the mirrors of the FP installed in two distant vacuum chambers suspended with attenators of ambient vibrations of the type developed for interferometric gravitational wave detectors. The separation of the two optical halves seems to limit the sensitivity of their apparatus. The finesse is below 10^5 OSQAR at CERN: uses a LHC dipole magnet 15 m long that can reach a 9 T field. The ellipsometer will exploit a FP to maximize the number of reflections and a novel optical techique to modulate the MBV effect. Since it is not feasible to set the LHC magnet in rotation and a modulation of the LHC magnet field intensity could be achieved only at very low frequency, the experiment foresees to modulate the polarization of the light entering the ellipsometer by setting in rotation the polarization plane. 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 33

PVLAS Ferrara on 3 competing experiments (II) n n According to our experience in this set-up the rotation of the polarization will generate a very large signal due to the intrinsic birefringence of the FP mirrors. BMV in Toulouse: homodyne, high intensity magnetic field, employing pulsed magnets (few ms), 40 cm long, that have already reached peak intensities in excess of B = 15 T, L = 0. 5 m total length, 5 shots/hour. Finesse 10^5, 10^(-7) per square root Hertz ellipticity sensitivity. For ten times improvement in sensitivity, it takes 650 years of continuous datataking. 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 34

Comparisons on the N 2 magnetic birefringence measurement PVLAS 2004 Q&A 2009 BMV 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 35

(Pseudo)scalar field: WEP & EEP in EM field (Pseudo)scalar-Photon Interaction Modified Maxwell Equations Polarization Rotation in EM Propagaton (Classical effect) Constraints from CMB polarization observation This talk 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 36

Galileo’s experiment on inclined plane (Contemporary painting of Giuseppe Bezzuoli) Galileo Equivalence Principle: Universality of free-fall trajectories 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 37

GP-B and Rotational EP 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 38

Einstein Equivalence Principle n EEP: (Einstein Elevator) Local physics is that of Special relativity n Study the relationship of Galileo Equivalence Principle and EEP in a Relativistic Framework: 2011. 12. NTHU framework Foundations of Classical Electrodynamics and PPM Framework W-T Ni 39

Electromagnetism： Charged particles and photons Special Relativity framework Galileo EP constrains to： (Pseudo)scalar-Photon Interaction 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 40

Various terms in the Lagrangian (W-T Ni, Reports on Progress in Physics, next month /also in ar. Xiv) 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 41

Empirical Constraints: No Birefringence 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 42

Empirical Constraints from Unpolarized EP Experiment: constraint on Dilaton for EM: φ = 1 ± 10^(-10) Cho and Kim, Hierarchy Problem, Dilatonic Fifth, and Origin of Mass, Ar. Xiv 0708. 2590 v 1 (4+3)-dim unification with G=SU(2), L<44 μm (Kapner et al. , PRL 2007) L<10 μm (Li, Ni, and Pulido Paton, Ar. Xiv 0708. 2590 v 1 Lamb shift in Hydrogen and Muonium gr-qc 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 43

Emprirical constraints: H g (One Metric) 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 44

Constraint on axion: φ < 0. 1 Solar-system 1973 (φ < 10^10) Metric Theories of Gravity n General Relativity n Einstein Equivalence Principle recovered n n For a recent exposition, see Hehl & Obukhov Ar. Xiv: 0705. 3422 v 1 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 45

Change of Polarization due to Cosmic Propagation n n The effect of φ is to change the phase of two different circular polarizations of electromagnetic-wave propagation in gravitation field and gives polarization rotation for linearly polarized light. [6 -8] Polarization observations of radio galaxies put a limit of Δφ ≤ 1 over cosmological distance. [9 -14] Further observations to test and measure Δφ to 10 -6 is promising. The natural coupling strength φ is of order 1. However, the isotropy of our observable universe to 10 -5 may leads to a change (ξ)Δφ of φ over cosmological distance scale 10 -5 smaller. Hence, observations to test and measure Δφ to 106 are needed. 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 46

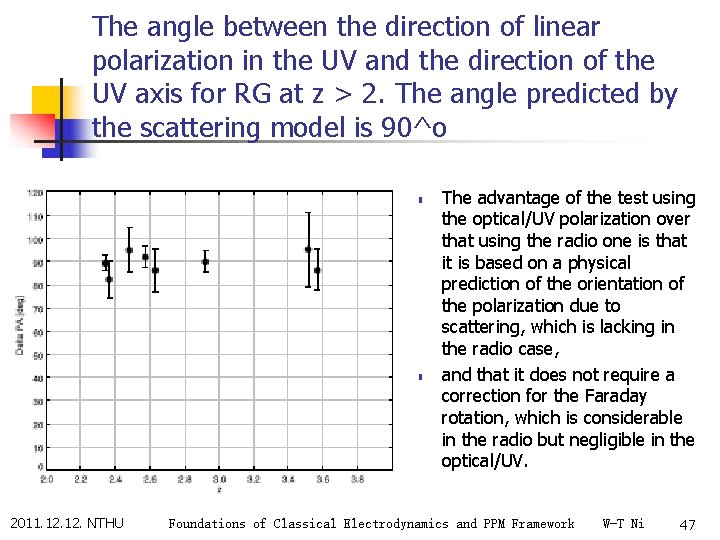
The angle between the direction of linear polarization in the UV and the direction of the UV axis for RG at z > 2. The angle predicted by the scattering model is 90^o n n 2011. 12. NTHU The advantage of the test using the optical/UV polarization over that using the radio one is that it is based on a physical prediction of the orientation of the polarization due to scattering, which is lacking in the radio case, and that it does not require a correction for the Faraday rotation, which is considerable in the radio but negligible in the optical/UV. Foundations of Classical Electrodynamics and PPM Framework W-T Ni 47

2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 48

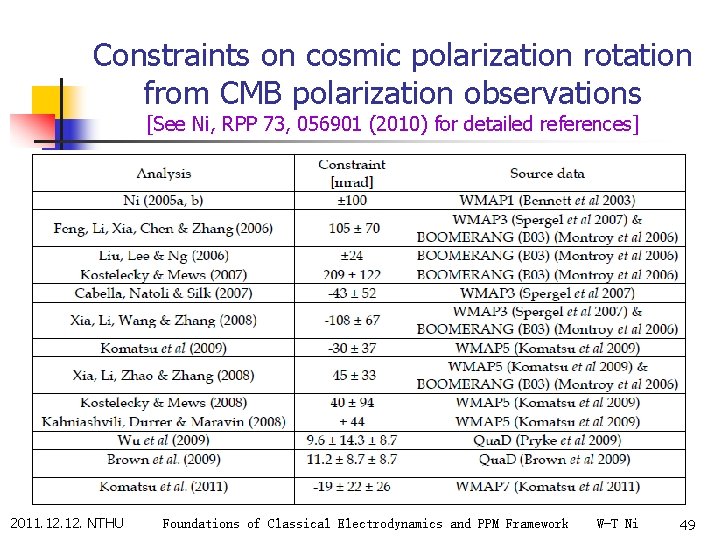
Constraints on cosmic polarization rotation from CMB polarization observations [See Ni, RPP 73, 056901 (2010) for detailed references] 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 49

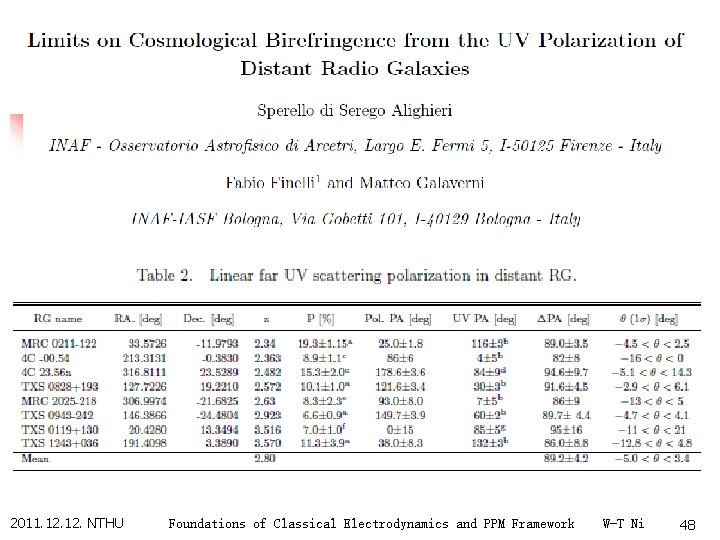
CMB Polarization Observation n In 2002, DASI microwave interferometer observed the polarization of the cosmic background. With the pseudoscalar-photon interaction , the polarization anisotropy is shifted relative to the temperature anisotropy. In 2003, WMAP found that the polarization and temperature are correlated to 10σ. This gives a constraint of 10 -1 rad or 6 degrees of the cosmic polarization rotation angle Δφ. 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 50

CMB Polarization Observation n n In 2005, the DASI results were extended (Leitch et al. ) and observed by CBI (Readhead et al. ) and CAPMAP (Barkats et al. ) In 2006, BOOMERANG CMB Polarization DASI, CBI, and BOOMERANG detections of Temperature-polarization cross correllation Qua. D Planck Surveyor was launched last year with better polarization-temperature measurement sensitivity. Sensitivity to cosmic polarization rotation Δφ of 10 -2 -10 -3 expected. 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 51

References 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 52

Space contribution to the local polarization rotation angle -- [μΣ 13φ, μΔxμ] = |▽φ| cos θ Δx 0. The time contribution is φ, 0 Δx 0. The total contribution is (|▽φ| cos θ + φ, 0) Δx 0. (Δx 0 > 0) Intergrated: φ(2) - φ(1) 1: a point at the decoupling epoch 2: observation point 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 53

Variations and Fluctuations n n Rotation φ(2) - φ(1) δφ(2) - δφ(1): δφ(2) variations and fluctuations at the last scattering surface of the decoupling epoch; δφ(1), at present observation point, fixed <[δφ(2) - δφ(1)]^2> variance of fluctuation ~ [couplingξ × 10^(-5)]^2 The coupling depends on various cosmological models 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 54

COSMOLOGICAL MODELS n n n n PSEUDO-SCALAR COSMOLOGY, e. g. , Brans. Dicke theory with pseudoscalar-photon coupling NEUTRINO NUMBER ASYMMETRY BARYON ASYMMETRY SOME other kind of CURRENT LORENTZ INVARIANCE VIOLATION CPT VIOLATION DARK ENERGY (PSEUDO)SCALAR COUPLING OTHER MODELS 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 55

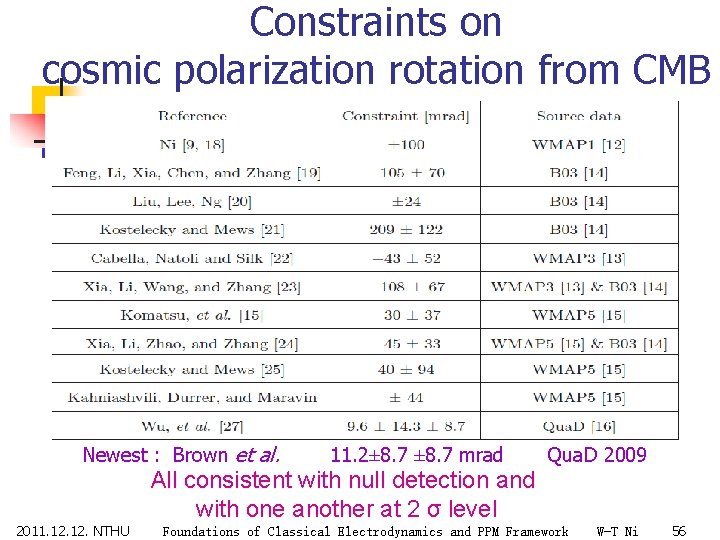
Constraints on cosmic polarization rotation from CMB Newest : Brown et al. 2011. 12. NTHU 11. 2± 8. 7 mrad Qua. D 2009 All consistent with null detection and with one another at 2 σ level Foundations of Classical Electrodynamics and PPM Framework W-T Ni 56

Outlook n n Precision tests of Classical Electrodynamics will continue to serve physics community in frontier research, in the quantum regime, in gravitation and in cosmology Thank you for your attention 2011. 12. NTHU Foundations of Classical Electrodynamics and PPM Framework W-T Ni 57