Foucaults Speed of Light Measurement The speed of

Foucault’s Speed of Light Measurement

The speed of light – long distances • How long does it take light to travel: – To the nearest star? • About four years – To Earth from the Sun? • About ten minutes – Around the circumference of the Earth? • About a tenth of a second

The speed of light – short distances • How long does it take light to travel – Across an atom? • About an attosecond (10 -18 s) – Across a computer chip? • About a picosecond (10 -13 s) – One foot? • About a nanosecond (10 -9 s) – Across the hall and back? • About a tenth of a microsecond (10 -7 s)

History of the speed of light • 1667: Galileo Galilei: “At least 10 times faster than sound” – Passing a message to an assistant • 1675: Ole Roemer: 200 000 km/s – Watching orbits of Jupiter’s moons • 1728: James Bradley: 301 000 km/s – Stellar aberration

History of the speed of light • 1849: Hippolyte Louis Fizeau: 313 000 km/s – Toothed wheel • 1926: Leon Foucault: 299 796 m/s – Rotating mirror • “True value”: 299 792 458 m/s

How does the experiment work? 1. Light bounces off a rotating mirror to a distant mirror 2. By the time it gets back to the first mirror, it has rotated through a small angle 3. This moves the reflected beam by a small amount that can be measured

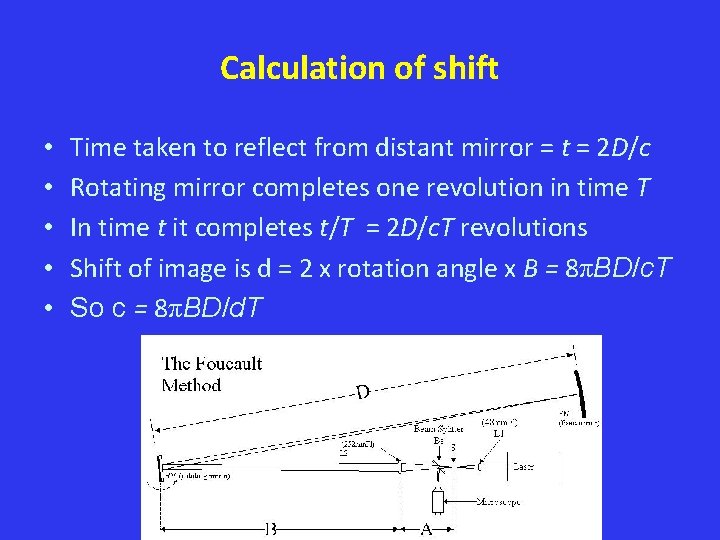
Calculation of shift • • • Time taken to reflect from distant mirror = t = 2 D/c Rotating mirror completes one revolution in time T In time t it completes t/T = 2 D/c. T revolutions Shift of image is d = 2 x rotation angle x B = 8πBD/c. T So c = 8πBD/d. T

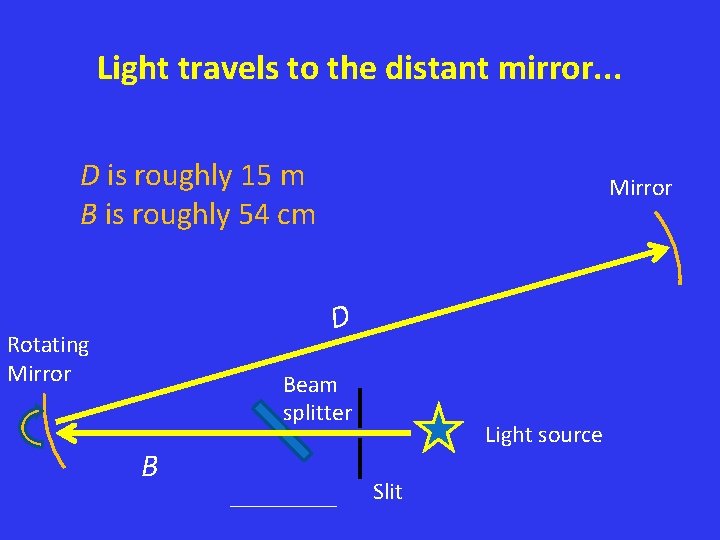
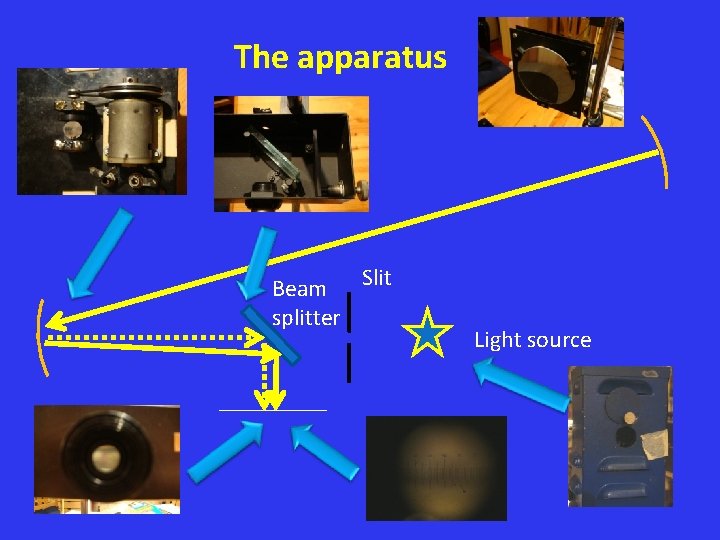
Light travels to the distant mirror. . . D is roughly 15 m B is roughly 54 cm Mirror D Rotating Mirror Beam splitter B Light source Slit

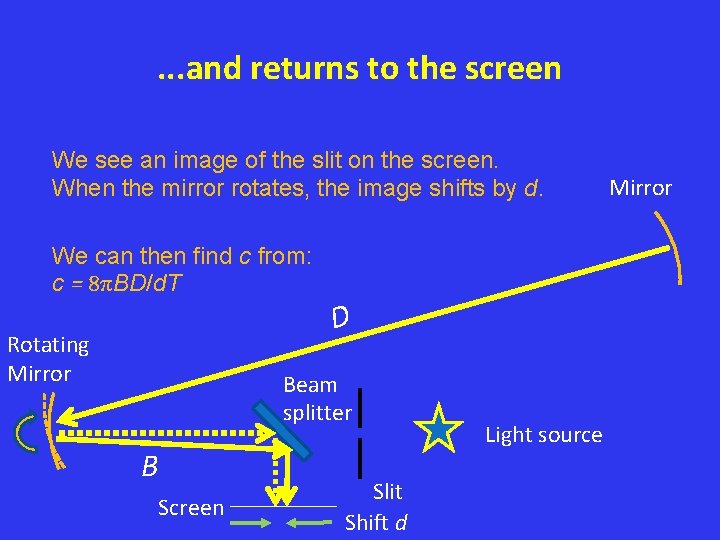
. . . and returns to the screen We see an image of the slit on the screen. When the mirror rotates, the image shifts by d. We can then find c from: c = 8πBD/d. T D Rotating Mirror Beam splitter B Screen Slit Shift d Light source Mirror

The apparatus Beam Slit splitter Light source

Measuring the rotation speed • A photodiode next to the rotating mirror sees a flash of light each time the mirror rotates – Creates a short voltage pulse • An oscilloscope allows us to measure the time between the flashes T

Results • For each measurement we need: – The number of divisions moved to find d • One division = 0. 1 mm – – The time between pulses = time for one rotation T D is equal to 15 m B is equal to 54 cm Then use c = 8πBD/d. T

Applications of c • Precision measurements of c were made by measuring the wavelength and frequency of laser light – Then use c = λ / f – Need ultra-stable laser • Now c has a defined value these techniques are used to make length standards (for precision measurements) – Manufacturing – surveying

Applications of c • Spectroscopy in fundamental physics – Measuring the spectrum of atoms allows us to test fundamental principles like matter/antimatter symmetry – Tests of Quantum Electro-Dynamics

Applications of c • Search for gravitational waves – Tiny distortions of space generated by accelerating masses – Looking for movements less than size of nucleus over 3 km

Thank you for listening!