Forze Conservative Definizione Il lavoro svolto da una

Forze Conservative • Definizione: Il lavoro svolto da una forza conservativa non dipende dal percorso effettuato. • Andando da P a Q lungo il cammino 1 si farà un lavoro WPQ 1 e se si va da Q a P lungo lo stesso cammino il lavoro dovrà essere -WQP 1 WPQ 1 = -WQP 1 Se posso andare da P a Q compiendo sempre lo stesso lavoro indipendentemente dal percorso allora posso andare la P a Q lungo S 1 e tornare da Q a P lungo S 2 ovvero WPQ 1 = -WQP 2 WPQ 1 + WQP 2 = 0 Q S 1 S 2 P • Allora una forza di dice conservativa quando il lavoro svolto lungo un cammino chiuso è nullo. • Il lavoro dipende solo dalle posizioni iniziale e finale in cui si trova il corpo.

Forze non conservative • Le forze sono non conservative quando il lavoro fatto lungo un cammino chiuso non è nullo: Attrito… Q • Nel caso in figura, l’attrito compie lavoro sia se S 1 va da P a Q lungo il tragitto 1, sia se si va da Q a P lungo il tragitto 2. S 2 • Quindi la forza d’attrito è una forza non conservativa. P

Conservazione dell’energia e del momento angolare

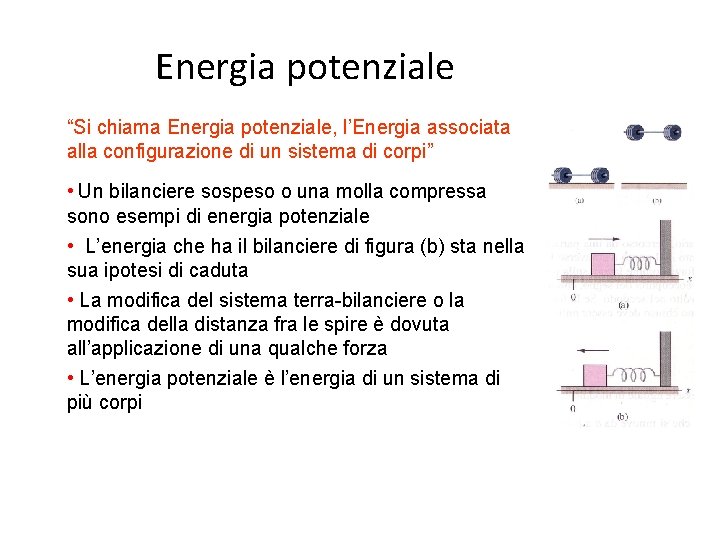
Energia potenziale “Si chiama Energia potenziale, l’Energia associata alla configurazione di un sistema di corpi” • Un bilanciere sospeso o una molla compressa sono esempi di energia potenziale • L’energia che ha il bilanciere di figura (b) sta nella sua ipotesi di caduta • La modifica del sistema terra-bilanciere o la modifica della distanza fra le spire è dovuta all’applicazione di una qualche forza • L’energia potenziale è l’energia di un sistema di più corpi

Energia Potenziale e Forze conservative • Portare una tegola su un soffitto o comprimere una molla, aumenta l’energia potenziale della tegola o della molla. • Sia la forza di gravità, che la forza elastica, devono fare un lavoro negativo per dare alla palla e alla molla più energia potenziale, scriveremo quindi che la variazione di energia potenziale è pari al lavoro fatto: DU = - w • Si fa un lavoro w 1 per variare la configurazione del sistema e si fa lavoro w 2 per ripristinarla. • Ovviamente w 1 = w 2 se la forza che ha fatto il lavoro è una forza conservativa.

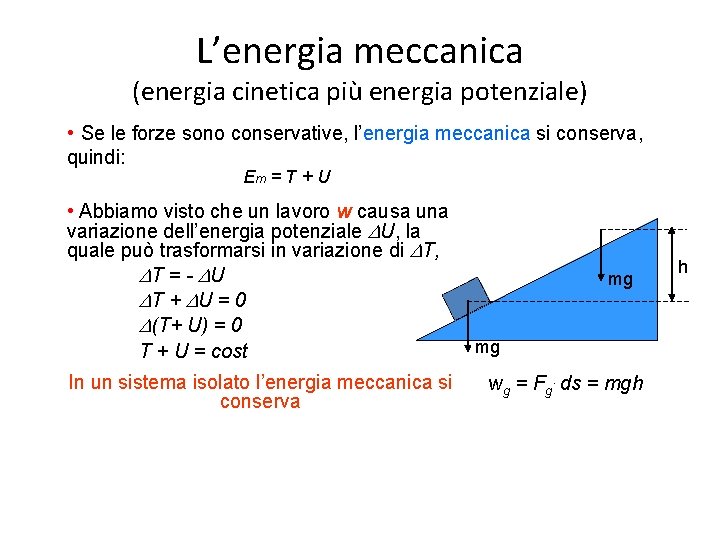
L’energia meccanica (energia cinetica più energia potenziale) • Se le forze sono conservative, l’energia meccanica si conserva, quindi: Em = T + U • Abbiamo visto che un lavoro w causa una variazione dell’energia potenziale DU, la quale può trasformarsi in variazione di DT, DT = - DU DT + DU = 0 D(T+ U) = 0 T + U = cost In un sistema isolato l’energia meccanica si conserva mg mg wg = Fg. ds = mgh h

Forze conservative: Il pendolo • Un pendolo ideale è formato da un filo inestensibile e da una massa puntiforme. • Il pendolo trasforma la sua energia potenziale, datagli dallo spostamento che lo ha portato ad una quota h, in energia cinetica e poi di nuovo in energia potenziale. • Il processo durerebbe all’infinito se non ci fossero attriti e altre resistenze vincolari. In un sistema isolato la variazione dell’energia meccanica è nulla

Forza derivata da un potenziale • Dalla relazione base che definisce il lavoro abbiamo: dw = F(x) ∙ dx • E dalla relazione che lega il lavoro con la variazione dell’energia potenziale sappiamo che dw = - d. U(x) • Quindi una forza si può ricavare dalla derivata del potenziale con il segno cambiato F(x) = - d. U(x)/dx • Esempi: 1) U(x) = ½ kx 2 (potenziale elastico) 2) 2) U(y) = mgy (potenziale gravitazionale) • Se il potenziale ha una forma analitica, la forza è individuata come l’opposto della derivata del potenziale 1) F(x) = - d(½ kx 2)/dx = - kx 2) F(y) = - d(mgy)/dy = - mg

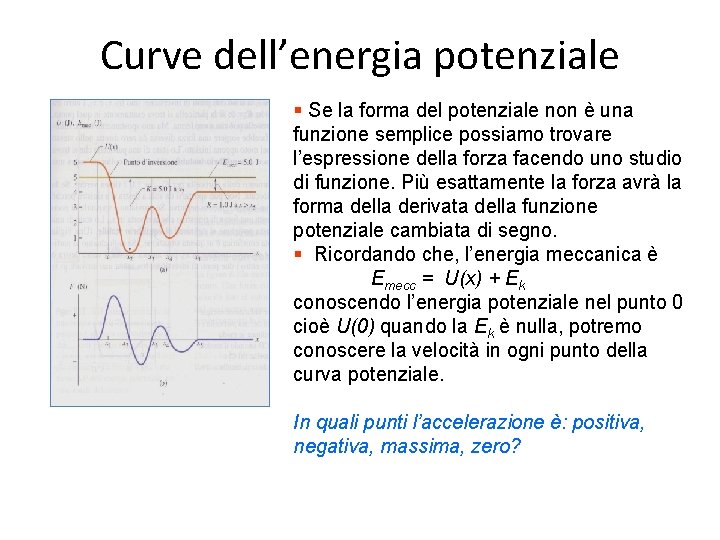
Curve dell’energia potenziale § Se la forma del potenziale non è una funzione semplice possiamo trovare l’espressione della forza facendo uno studio di funzione. Più esattamente la forza avrà la forma della derivata della funzione potenziale cambiata di segno. § Ricordando che, l’energia meccanica è Emecc = U(x) + Ek conoscendo l’energia potenziale nel punto 0 cioè U(0) quando la Ek è nulla, potremo conoscere la velocità in ogni punto della curva potenziale. In quali punti l’accelerazione è: positiva, negativa, massima, zero?

Conservazione del momento angolare • Le grandezze fisiche si conservano rivestono un ruolo importante perché permettono di prevedere la dinamica dei moti a seguito di eventi significativi. ttot = d. L/dt. • Se il momento delle forze è nullo e il sistema è isolato, L sarà costante; cioè Lf = Li. • La natura vettoriale di L implica la conservazione lungo tutte e tre le direzioni dello spazio

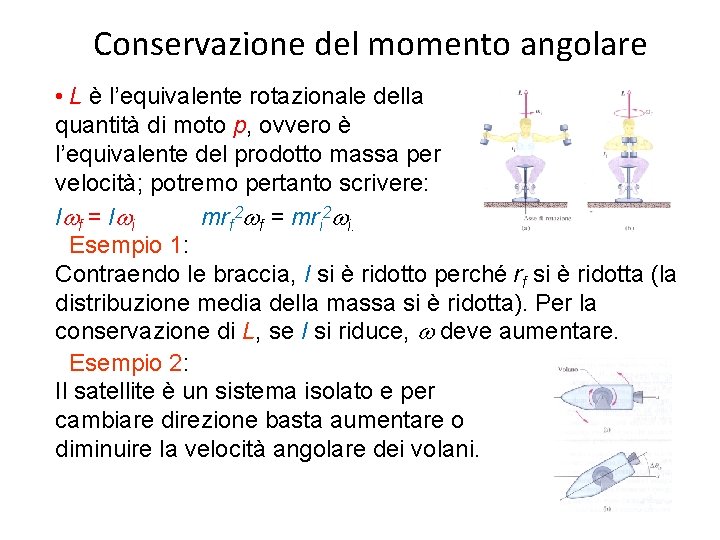
Conservazione del momento angolare • L è l’equivalente rotazionale della quantità di moto p, ovvero è l’equivalente del prodotto massa per velocità; potremo pertanto scrivere: I wf = I wi mrf 2 wf = mri 2 wi. Esempio 1: Contraendo le braccia, I si è ridotto perché rf si è ridotta (la distribuzione media della massa si è ridotta). Per la conservazione di L, se I si riduce, w deve aumentare. Esempio 2: Il satellite è un sistema isolato e per cambiare direzione basta aumentare o diminuire la velocità angolare dei volani.

Ancora sulla conservazione di L § Nella figura è riportato uno studente seduto su uno sgabello girevole fermo. In mano, ha un volano in movimento dotato di momento angolare L. § Se lo studente ruota di 180° l’asse del volano lo sgabello e lo studente inizieranno a ruotare. § Il cambiamento di direzione imposto al volano determina che il momento angolare dello sgabello più lo studente dovrà essere: Lvi = - Lvf + 2 L. § Cosa sarebbe successo se il volano avesse avuto originariamente un momento angolare orizzontale?