FORMULE DI GAUSSGREEN NEL PIANO CAMPI VETTORIALI Argomenti

































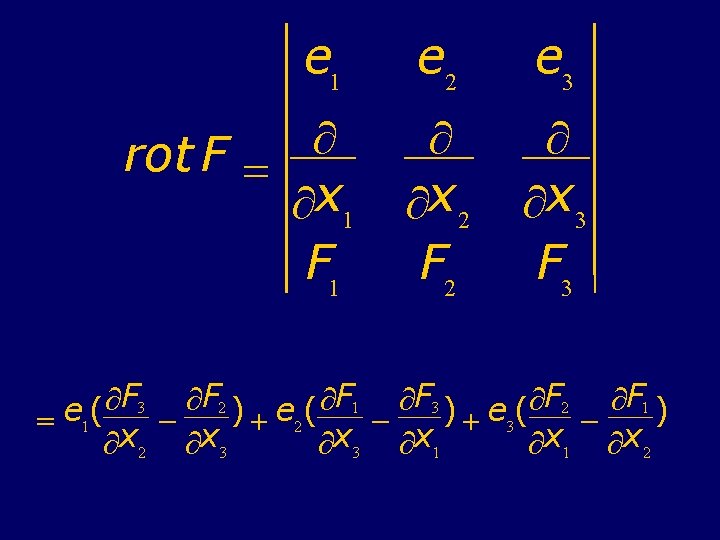

- Slides: 38

FORMULE DI GAUSS-GREEN NEL PIANO. CAMPI VETTORIALI

Argomenti della lezione è Formule di Gauss. Green nel piano è Campi vettoriali (forme differenziali)

FORM�ULE DI GAUSS-GREEN NEL PIANO

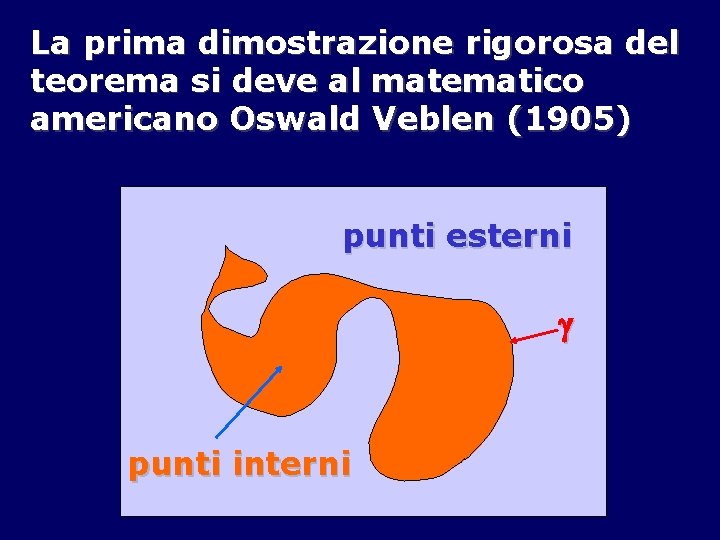
Un teorema di topologia piana fortemente intuitivo, ma difficile da dimostrare, è il famoso teorema di Jordan (Marie Ennemond Camille) (1887): Se (t) è una curva continua semplice chiusa in R 2, il suo sostegno divide il piano in due aperti: uno limitato, detto dei punti interni alla curva; l’altro illimitato dei punti esterni

La prima dimostrazione rigorosa del teorema si deve al matematico americano Oswald Veblen (1905) punti esterni punti interni

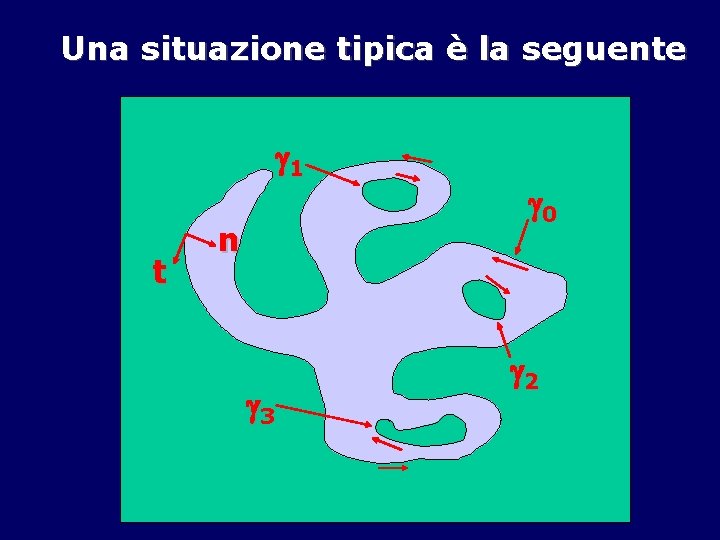
Un aperto connesso che ha come frontiera una curva generalmente regolare, semplice, chiusa si dice semplicemente connesso. Se la frontiera del dominio aperto è costituita da più curve generalmente regolari semplici e chiuse i sostegni delle quali sono contenuti nei punti interni di un’unica curva e che hanno le chiusure dei punti interni a due disgiunte, diremo che il dominio è molteplicemente connesso

Una situazione tipica è la seguente 1 t n 3 0 2

Evidentemente la frontiera del dominio A è trascurabile e quindi il dominio è misurabile secondo PJ. Infatti la frontiera è l’unione di un numero finito di grafici di funzioni continue. Un tale dominio si dirà un dominio regolare. Una curva chiusa generalmente regolare ha un’orientazione intrinseca: siano t il versore tangente e n un versore normale.

Diremo che l’orientazione della curva è positiva se, essendo la coppia t n congruente ai versori degli assi (i e j o e 1 ed e 2), la normale n punta verso l’interno di . Tale orientazione si dice anche antioraria. Se il bordo di A è dato da più curve chiuse, l’orientazione positiva della curva esterna è antioraria mentre quella delle curve interne è oraria

Teorema (Formule di Gauss-Green o di Green-Riemann) Sia A un dominio regolare, di frontiera ∂A = = 0 + 1 +. . + k positivamente orientata e siano X(x, y) e Y(x, y)

continue su A ∂A insieme con le loro derivate Xy(x, y) e Yy(x, y). Allora si ha k Xdx ò òòA Xy (x, y)dxdy = - +ò¶A Xdx = - å i = 0 +g i k Ydy ò òòA Yx (x, y)dxdy = +ò¶A Ydy = å i = 0 +g i

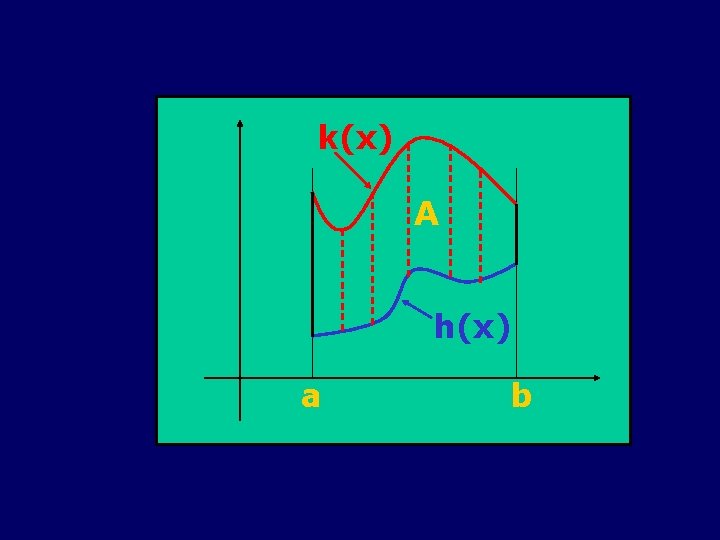
òò (Yx - X y )dxdy = +ò¶A(Xdx + Ydy) A Dimostreremo la formula in un caso semplificato, nel quale A è un dominio normale rispetto all’asse x Sia dunque A = {(x, y) : a ≤ x ≤ b, h(x) ≤ y ≤ k(x)} con h(x) e k(x) di classe C 1([a, b])

Allora b k (x) a h(x) òò X y (x, y)dxdy = ò dx ò X y dy = A b òa ( X(x, k(x)) - X(x, h(x)))dx = - òAXdx +¶ Si è tenuto conto che dx è nullo lungo i lati verticali

k(x) A h(x) a b

In modo analogo si dimostra la seconda formula; la terza è la somma delle due precedenti e una simmetrizzazione delle stesse. Osserviamo che quanto abbiamo dimostrato è il primo passo per una dimostrazione completa del teorema come l’abbiamo enunciato. Tuttavia i metodi per giungere a una dimostrazione rigorosa della formula travalicano le nostre possibilità e gli scopi di questo corso

È interessante l’applicazione della formula precedente al calcolo di aree piane. Sia una curva piana generalmente regolare semplice chiusa che forma il bordo del dominio A. Poiché la costante 1 è la derivata rispetto a x di x o rispetto a y di y

m(A) = òò dxdy = òA xdy = - òAydx = +¶ +¶ A 1 ò (xdy ydx) 2 +¶ A La formula è particolarmente utile quando si conoscono le equazioni parametriche di = +∂A.

Esempi 1) Si calcoli l’area dell’ellisse di semiassi a e b L’equazione parametrica dell’ellisse è x= a cos t, y = b sen t 0 ≤ t ≤ 2π 2 p m(A) = òòA dxdy = ò ab cos 2 t dt +¶A 0 = πab

2) Si calcoli l’area racchiusa dal cappio del “folium Cartesii”, d’equazioni ìx = t(t - 1) í ïîy = t(t - 1)(2 t - 1) t Î R Il cappio si ottiene prendendo 0≤t≤ 1

Si vuole calcolare 1 ò x(t)y ¢(t)dt = ò (6 t - 12 t + 7 t - t)dt = 30 0 0 1 1 4 3 2

Il “foglio di Cartesio”

CAMPI VETTORIALI (FORME DIFFERENZIALI)

Supponiamo che ad ogni punto di un aperto A contenuto in R 3 (R 2) sia assegnato un vettore F di R 3 (R 2). Diremo che in A è assegnato un campo vettoriale: F = (F 1, F 2, F 3)T Se invece, in ogni punto di A è assegnato il valore di una funzione f(x, y, z) diremo che abbiamo a che fare con un campo scalare

Nella Fisica abbondano gli esempi di campi vettoriali (campo di velocità in un fluido, campo elettrico o magnetico o campo gravitazionale nel piano o nello spazio) e di campi scalari (pressione, densità o temperatura in un fluido o in un corpo piano o solido) In Matematica si preferisce parlare invece di forme differenziali lineari in R 2 o in R 3 o semplicemente di funzioni (forme di grado 0)

Useremo il linguaggio della Fisica, formalmente più semplice. Dato il campo vettoriale F in R 3 sappiamo che cosa significa 1 òg F , t ds = ò 0 F(g (t)), g ¢(t) dt che, nel caso F sia una forza, dà il lavoro di F per lo spostamento lungo .

Un campo vettoriale F su A si dice conservativo se esiste una funzione U(x, y, z) definita sull’aperto A, tale che F = grad U = U La funzione U(x, y, z) si dice un potenziale di F. Si noti che se U(x, y, z) è un potenziale, anche U(x, y, z) + costante è un potenziale

Teorema Sia F un campo conservativo continuo su un aperto A Rm e : [a, b] Rm una curva regolare con (I) A, allora per ogni x, y A l’integrale di linea

òg F , t ds = U(y) - U(x) dipende solo da x e y Infatti 1 òg F , t ds = ò (F 1 x 1¢(t) + F 2 x 2¢(t) + F 3 x 3¢(t)) dt 0

1 = ò (Ux (x 1(t), x 2 , x 3 )x 1¢(t) + Ux x 2¢(t) + 0 1 2 + Ux x 3¢(t)) dt 3 1 d = ò (U(x 1(t), x 2 (t), x 3(t))dt = U(g (1)) - U(g (0)) 0 dt = U(y) - U(x), come si doveva dimostrare

Teorema Sia F un campo vettoriale continuo su un aperto connesso A Rm. Allora F è conservativo se e solo se, per ogni x, y A e per ogni 1 e 2

congiungenti x con y è òg F , t ds = gò F, t ds 1 2 Se F è conservativo, per il teorema precedente la proprietà vale. Mostriamo che vale il viceversa; per semplicità ci ambientiamo in R 2

Se x 0 è un punto arbitrario di A, definiamo U(x 1, x 2 ) = ò F, t ds g essendo un qualsiasi cammino congiungente x 0 con x. Se x’ = (x 1+h, x 2)T e è il segmento congiungente x con x’, si ha

U(x 1 + h, x 2 ) - U(x 1 , x 2 ) = h ò F, t ds d h 1 1ò F (x th, x )hdt F (x = = 1 1 + x h, x 2 ) 1 1 + 2 h 0 con 0 ≤ ≤ 1. Per la continuità del campo, se h 0 ¶U F (x , x ) = 1 1 2 x ¶ 1

Analogamente si valuta la derivata rispetto a x 2 Si trova poi che

Corollario Sia F un campo vettoriale continuo su un aperto connesso A Rm. Allora F è conservativo se e solo se, per ogni curva gen. regolare chiusa è

òg F , t ds = 0 Se F è un campo vettoriale di classe C 1(A) diremo rotore di F, rot F = F il seguente vettore
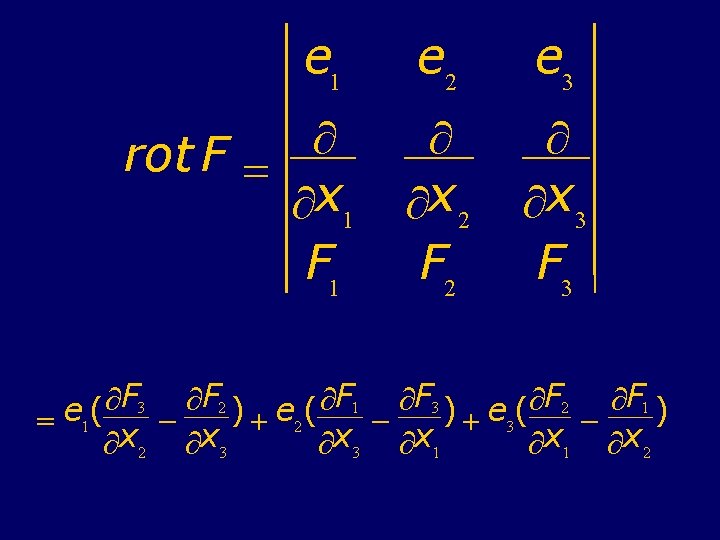
e 1 e 2 e 3 ¶ rot F = ¶x 1 F 1 ¶ ¶x 2 F 2 ¶ ¶x 3 F F F F ¶ ¶ ¶ 3 2 1 e ( ) = 1 + 2 + 3 ¶x 2 ¶x 3 ¶x 1

Un campo vettoriale F di classe C 1(A) si dice irrotazionale se rot F = 0 È banale osservare che ogni campo conservativo di classe C 1(A) è irrotazionale Se A è connesso e semplicemente connesso, si può dimostrare che la condizione di irrotazionalità è anche sufficiente.