Formulations and Reformulations in Integer Programming Michael Trick

Formulations and Reformulations in Integer Programming Michael Trick Carnegie Mellon University Workshop on Modeling and Reformulation, CP 2004

Goals n n n Provide a perspective on what makes a “good” integer programming formulation for a problem Give examples on automatic versus manual reformulation of problems Outline some challenges in the automatic reformulation of integer programs (and perhaps constraint programs? )

Outline n n Quick review of key concepts in integer programming Two models q q n Truck-route contracting Traveling Tournament Problem General Comments

Integer Program (IP) Linear objective Minimize cx X: variables Subject to Linear constraints Ax=b l<=x<=u some or all of xj integral Makes things hard!

Rules of the Game n n n Must put in that form! Seems limiting, but 50 years of experience gives “tricks of the trade” Many formulations for same problem

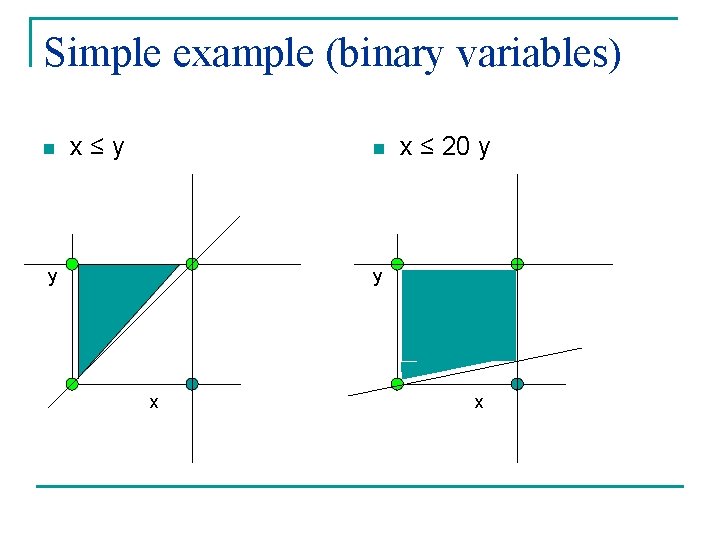
Simple example n n Variables x, y both binary (0 -1) variables Formulate requirement that x can be 1 only if y is 1 Formulation 1: x ≤ y; x, y {0, 1} Formulation 2: x ≤ 20 y; x, y {0, 1} Are they different? Do we care which we use?

Differences n n From a modeling point of view, they are the same: they both correctly model the given requirement From an algorithmic point of view, they may be different, depending on algorithm used

Solving Integer Programming problems n Most common method is some form of branch and bound q q q Use linear relaxation to bound objective value Branch on fractional values in linear relaxation solution Stop branching when subproblem is n n n Infeasible Integer Fathomed (cannot be better than best found so far)

Linear Relaxation Linear objective Minimize cx X: variables Subject to Linear constraints Ax=b l<=x<=u some or all of xj integral Makes things hard!

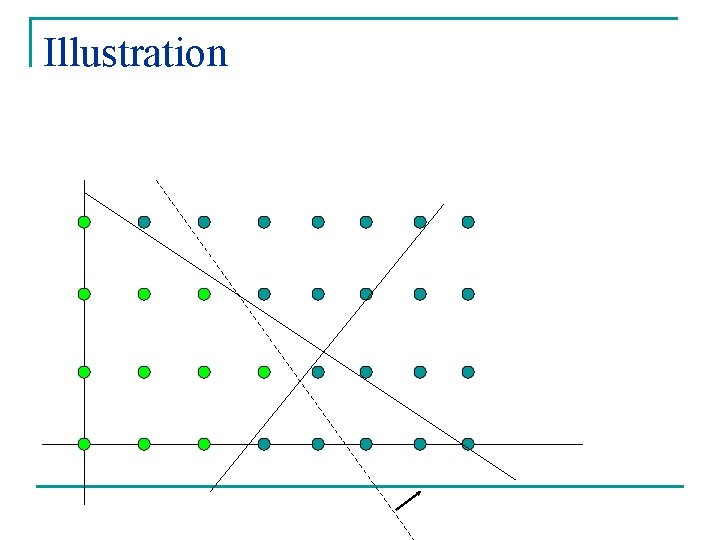
Illustration

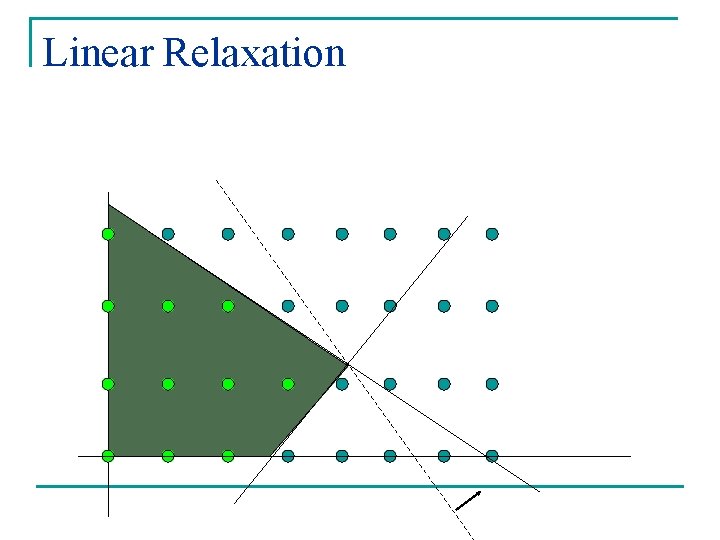
Linear Relaxation

Key is linear relaxation n If linear relaxation is very different from integer program then q q Choose wrong variables to branch on Fathoming will be done less often

Ideal Formulation gives convex hull of feasible integer points

Simple example (binary variables) n x≤y n y x ≤ 20 y y x x

Fundamental Mantra of Integer Programming Formulations Use formulations with good linear relaxations! This guideline is quite misleading! Other issues in formulations: avoiding symmetry issues, keeping problem size down, scaling, etc. that will not be covered here

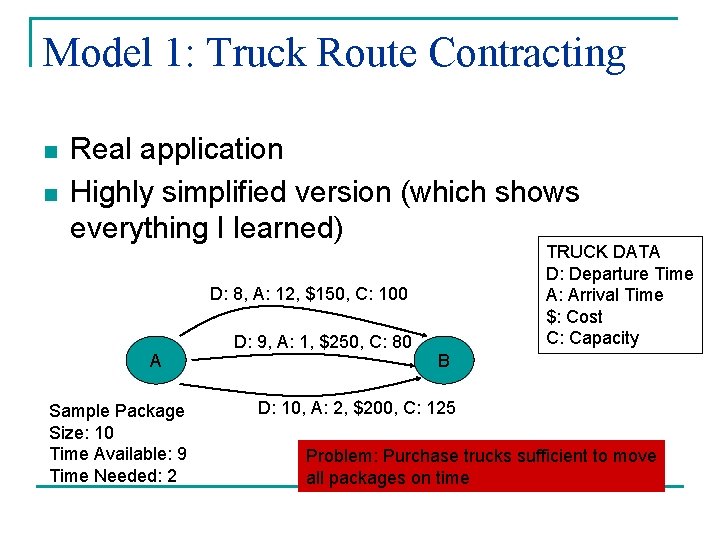
Model 1: Truck Route Contracting n n Real application Highly simplified version (which shows everything I learned) TRUCK DATA D: Departure Time A: Arrival Time $: Cost C: Capacity D: 8, A: 12, $150, C: 100 A Sample Package Size: 10 Time Available: 9 Time Needed: 2 D: 9, A: 1, $250, C: 80 B D: 10, A: 2, $200, C: 125 Problem: Purchase trucks sufficient to move all packages on time

Model Variables: y(i) = 1 if truck i purchased, 0 else x(j, i) = 1 if package j on i, 0 else Objective: Minimize truck costs Constraints: Packages fit on assigned truck Use only paid for trucks Every package on some truck No partial trucks or package splitting

Formulation: declarations model "Transportation Planning" uses "mmxprs" declarations TRUCKS = 1. . 10 PACKAGES = 1. . 20 capacity: array(TRUCKS) of real size: array(PACKAGES) of real cost: array(TRUCKS) of real can_use: array(PACKAGES, TRUCKS) of real x: array(PACKAGES, TRUCKS) of mpvar y: array(TRUCKS) of mpvar end-declarations capacity: = [100, 200, 100, 200] size : = [17, 21, 54, 45, 87, 34, 23, 45, 12, 43, 54, 39, 31, 26, 75, 48, 16, 32, 45, 55] cost : = [1, 1. 8, 1, 1. 8] can_use: =[0 -1 matrix whether package can go on truck]

Formulation: Constraints Total : = sum(i in TRUCKS) cost(i)*y(i) forall(i in TRUCKS) sum(j in PACKAGES) size(j)*x(j, i) <= capacity(i) ! (1) Packages fit forall (i in TRUCKS) sum (j in PACKAGES) x(j, i) <= NUM_PACKAGE*y(i) ! (2) use only ! paid for trucks forall (j in PACKAGES) sum(i in TRUCKS) can_use(j, i)*x(j, i) = 1 ! (3) every ! package on truck forall (i in TRUCKS) y(i) is_binary ! (4) no partial trucks forall (i in TRUCKS, j in PACKAGES) x(j, i) is_binary ! (5) no package splitting minimize(Total) end-model

“Improving the Formulation” n Every integer programming will immediately spot the improvements: forall (i in TRUCKS) sum (j in PACKAGES) x(j, i) <= NUM_PACKAGE*y(i) ! (2) use only ! paid for trucks should be replaced with forall (i in TRUCKS, j in PACKAGES) x(j, i) <= y(i) !(2’) tighter formulation which we saw as “tighter” (though bigger)

Other improvements n Integer programmers are good at spotting opportunities: forall(i in TRUCKS) sum(j in PACKAGES) size(j)*x(j, i) <= capacity(i) ! (1) Packages fit Can be strengthened with forall(i in TRUCKS) sum(j in PACKAGES) size(j)*x(j, i) <= capacity(i)*y(i) ! (1’) Packages fit

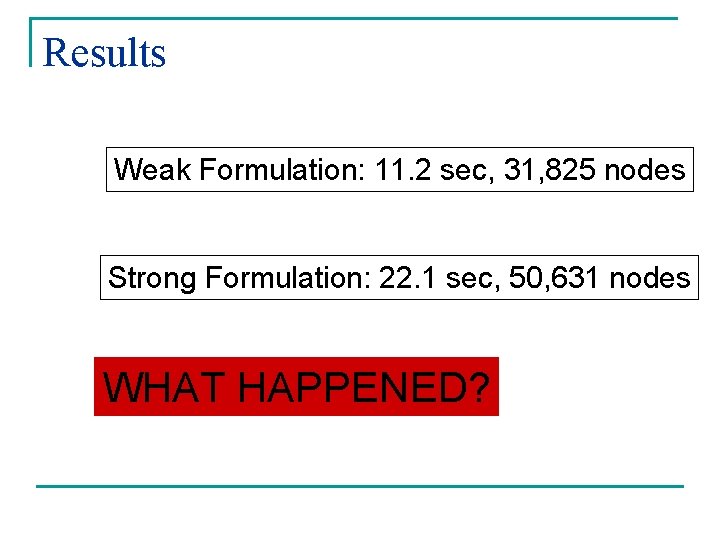
Results Weak Formulation: 11. 2 sec, 31, 825 nodes Strong Formulation: 22. 1 sec, 50, 631 nodes WHAT HAPPENED?

Automatic versus Manual Reformulations n n XPRESS-MP (ILOG’s CPLEX will work the same) “knows” about this form of tightening. It will do it automatically In fact, it will do it “better”, only including constraints that the linear relaxation points to as relevant Automatic reformulation trumps manual reformulation in this case!

Naïve code n If you use a naïve code that doesn’t understand this, then tightened formulation is critical: Weak formulation: Unsolved after 3600 seconds (gap is 1. 22 – 8. 4) Strong formulation: 1851 seconds, 2. 4 million nodes But who would use such a code for real work?

Gets more confusing n Consider the constraint sum(i in TRUCKS) capacity(i)*y(i) >= sum (j in PACKAGES)size(j) ! (6) Have sufficient capacity Such a constraint does not tighten the formulation (it is a linear combination of existing constraints): fundamental mantra says don’t add. Solution time: . 1 seconds, 1 node

What happened n XPRESS (and other sophisticated codes) knows a lot about “knapsack” constraints and does automatic tightening on those n Can’ identify knapsack constraint, but once identified by user, can tighten (a lot!).

Summary of model 1 n n Standard tightening methods by user makes things slower Creative addition of constraint that does not appear to tighten relaxation makes things much faster

Model 2: Traveling Tournament Problem Given an n by n distance matrix D= [d(i, j)] and an integer k find a double round robin (every team plays at every other team) schedule such that: q q The total distance traveled by the teams is minimized (teams are assumed to start at home and must return home at the end of the tournament), and No team is away more than k consecutive games, or home more than k consecutive games. (For the instances that follow, an additional constraint that if i is at j in slot t, then j is not at i in t+1. )

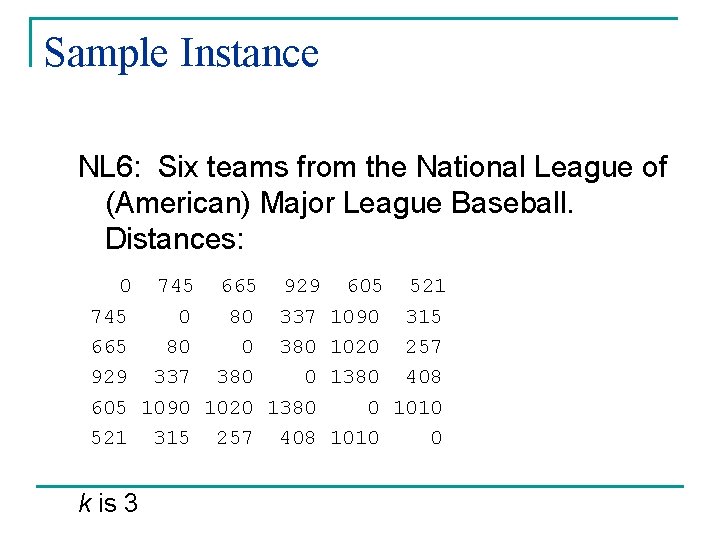
Sample Instance NL 6: Six teams from the National League of (American) Major League Baseball. Distances: 0 745 665 929 605 521 745 0 80 337 1090 315 665 80 0 380 1020 257 929 337 380 0 1380 408 605 1090 1020 1380 0 1010 521 315 257 408 1010 0 k is 3

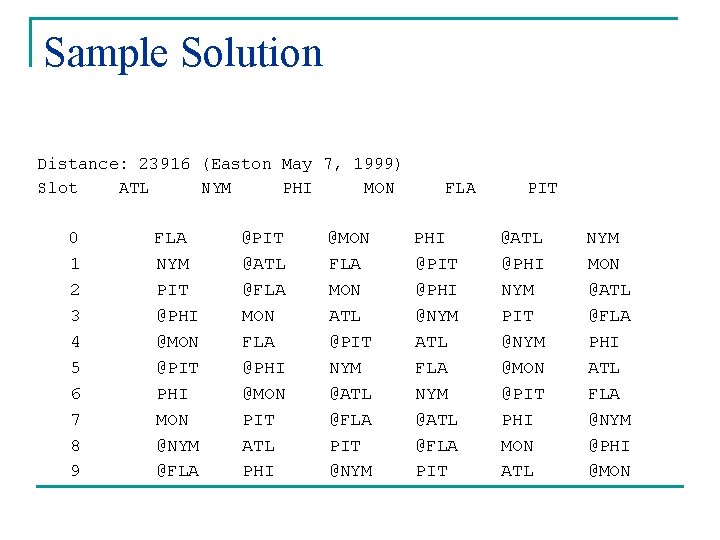
Sample Solution Distance: 23916 (Easton May 7, 1999) Slot ATL NYM PHI MON 0 1 2 3 4 5 6 7 8 9 FLA NYM PIT @PHI @MON @PIT PHI MON @NYM @FLA @PIT @ATL @FLA MON FLA @PHI @MON PIT ATL PHI @MON FLA MON ATL @PIT NYM @ATL @FLA PIT @NYM FLA PHI @PIT @PHI @NYM ATL FLA NYM @ATL @FLA PIT @ATL @PHI NYM PIT @NYM @MON @PIT PHI MON ATL NYM MON @ATL @FLA PHI ATL FLA @NYM @PHI @MON

Simple Problem, yes? NL 12. 12 teams Feasible Solution: 143655 (Rottembourg and Laburthe May 2001), 138850 (Larichi, Lapierre, and Laporte July 8 2002), 125803 (Cardemil, July 2 2002), 119990 (Dorrepaal July 16, 2002), 119012 (Zhang, August 19 2002), 118955 (Cardemil, November 1 2002), 114153 (Van Hentenryck January 14, 2003), 113090 (Van Hentenryck February 26, 2003), 112800 (Van Hentenryck June 26, 2003), 112684 (Langford February 16, 2004), 112549 (Langford February 27, 2004), 112298 (Langford March 12, 2004), 111248 (Van Hentenryck May 13, 2004). Lower Bound: 107483 (Waalewign August 2001)

Formulation as IP Straightforward formulation is possible: plays(i, j, t) = 1 if i at j in slot t n Need auxiliary variables location (i, j, t) = 1 if i in location j in slot t follows(i, j, k, t) = 1 I travels from j to k after slot t

Formulation n Rest of formulation in paper (pages 9 and 10 in proceedings) n Result is a mess q q n N=6 After 1800 seconds gap is 5434 – 25650 (optimal is 23, 916) Anything XPRESS is doing is not helping enough!

Reformulation • Sample Variables: @NY X 1 @MON @PHI @NY X 3 H H X 2 H H Y 1 Y 2

Constraints n One thing per time: X 1+X 2+Y 1+Y 2 1 @NY X 1 @MON @PHI H H X 2 Y 1 Y 2

Constraints n No Away followed by Away X 1+X 3 1 @MON @PHI @NY X 2 X 3

Rest of formulation n Rest of formulation is straightforward (in proceedings, looking more complicated than it needs to) n Result: initial relaxation (for n=6) 21, 624. 7 Optimal: 4136 seconds, 66, 000 nodes n

Strengthening the Constraints n Stronger: X 1+X 2+X 3+Y 2 1 @NY @MON @PHI @NY H X 1 X 2 X 3 H Y 2

Result Initial relaxation same, solution time a little longer What happened: “Strengthening” is type of clique inequality, known by XPRESS Without clique inequalities: unsolved after more than 36, 000 seconds

Conclusions for Model 2 n Initial formulation almost hopeless n Manual reformulation needed to redefine variables Then, automatic reformulation can improve results tremendously n

Questions n What is the role of manual versus automatic reformulation? q q n n Model 1: manual needed to identify hidden constraint Model 2: manual needed to redefine the variables Is this an ever-moving line, or are some aspects intrinsically difficult to determine? How can software be developed to better q q Do automatic reformulation Provide flexibility to experiment with different reformulations/reformulation levels

Resources n Introduction to Integer Programming (by Bob Bosch and me) and this talk q n Will be at http: //mat. tepper. cmu. edu/trick XPRESS-MP and ILOG’s OPL Studio provide great software to experiment with