formula weight molecular weight sum of the atomic

formula weight (molecular weight) - sum of the atomic weights of all atoms in the species Determine the MW of SCl 2 Determine the MW of calcium nitrate

mole – a quantity that contains 6. 022 x 1023 particles Avogadro’s #, N – 1 mole of anything = 6. 022 x 1023 particles

Amedeo Avogadro 1776 - 1856 Lorenzo Romano Amedeo Carlo Bernadette Avogadro di Quaregna e Cerreto

How many grams does 1 mole of lead, Pb weigh ? molar mass – one mole (6. 022 x 1023) of any substance is equal to the atomic weight of that substance (units are g/mole)

How many grams of Al are in 1 mole of Al atoms ? 26. 981538 g Al What is the mass of a single Al atom ? 26. 981538 amu What is the molar mass of Al ? 26. 981538 g/mole I have 26. 981538 g Al. How many atoms of Al do I have ? 6. 022 x 1023 atoms Al

Which container has more atoms: 207. 2 g Pb or 26. 981538 g Al ? same How many atoms are in 207. 2 g Pb ? 6. 022 x 1023 atoms Pb

Calculate the # moles in 4. 558 g K

Calculate the # moles in 38. 620 g H 2 O

Calculate the # grams in 3. 97 moles CO 2

Calculate the # molecules in 3. 704 g H 2 O

Calculate the # of moles of carbon, C in 5. 05 moles CO 2

Calculate the # moles Cl- anions in 6. 314 moles Ca. Cl 2

Calculate the # of hydrogen atoms in 14. 5 g CH 3 OH

Percent composition = mass of element x 100 total mass species Calculate the percentage composition of each element in chromium(III) oxide

empirical formula – formula containing the smallest, whole # ratio of atoms in a molecule Empirical Formula’s in Calculations 1. Calculate the moles of each substance 2. Divide each moles by the smallest number to get the empirical formula

A compound was analyzed and found to contain 7. 889 g sulfur and 11. 808 g oxygen. What is the empirical formula of the compound ?

An oxide of gold, Au, is analyzed and found to be 89. 11% Au (by wt. ) and 10. 89% oxygen (by wt. ). What is the empirical formula of compound ? * assume 100 g sample

How and When to round during empirical formula calculations D=1 Q ≈ 1. 5 D = (1)2 = 2 Q ≈ (1. 5)2 ≈ 3 D 2 Q 3 D=1 Q ≈ 1. 33 D = (1)3 = 3 Q ≈ (1. 33)3 ≈ 4 D 3 Q 4 D=1 Q = 1. 94748 ≈ 2 DQ 2

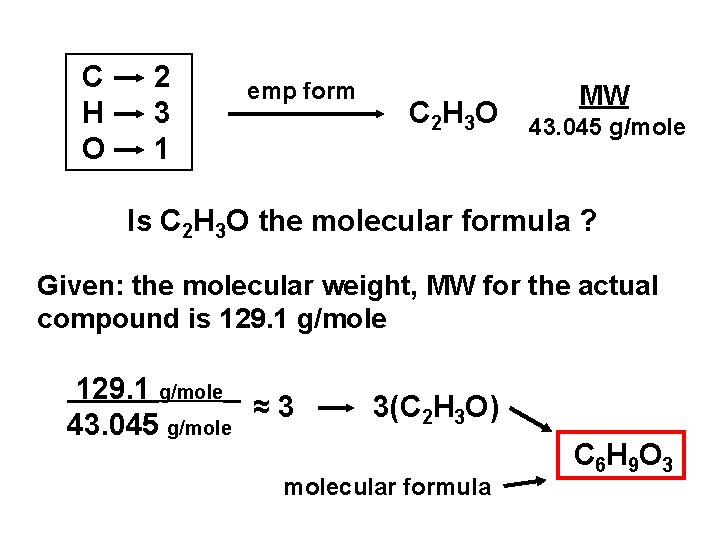
Empirical formula vs. Molecular formula 1. Calculations always reveal empirical formula 2. Must be given the molecular weight, MW, to determine actual molecular formula 3. Ratio the actual MW vs. the MW of empirical formula

C H O 2 3 1 emp form C 2 H 3 O MW 43. 045 g/mole Is C 2 H 3 O the molecular formula ? Given: the molecular weight, MW for the actual compound is 129. 1 g/mole ≈3 43. 045 g/mole 3(C 2 H 3 O) molecular formula C 6 H 9 O 3

hydrates – salts with loosely held H 2 O’s of hydration Na 2 SO 4· 7 H 2 O Mg(NO 2)2 · 3 H 2 O sodium sulfate heptahydrate magnesium nitrite trihydrate Ca. Cl 2 exists as a hydrate. 6. 267 g of hydrated calcium chloride was heated leaving 4. 731 g of dehydrated Ca. Cl 2. Determine: 1. the %water (by wt. ) in the hydrated salt 2. the empirical formula of the hydrated salt

balanced chemical reaction – same number of atoms of each element on either side of the arrow reactants – are on left side of the arrow; stuff being consumed in reaction products – are on right side of the arrow; stuff being formed in reaction arrow, – means equals, or produces, or gives

combustion rxn – when something burns and consumes oxygen, O 2

Balance reactions by adding coefficients to get the same number of each atom of each element on either side of the arrow Balancing Hints 1. Inspect the unbalanced rxn for 10 sec 2. Leave the free, uncombined elements alone until the end 3. Work with pencil so you can erase mistakes 4. Practice lots of hw problems

stoichiometry – a quantitative relationship between reactants and products via moles How many moles of H 2 O are obtained from the combustion of 3. 5 moles C 3 H 8 O ?

How many moles of O 2 are required to completely combust 12. 1 moles C 3 H 8 O ?

How many g of CO 2 can be obtained by combusting 3. 70 moles of C 3 H 8 O ?

Isopropyl alcohol, C 3 H 8 O was burned and 12. 5 g O 2 was consumed. How many g H 2 O was produced ?

Limiting reagent – reactant that runs out first Excess reagent – reactant left over after the rxn is finished Theoretical yield – maximum obtainable product (based on the limiting reagent) Percent yield = amount of product actually obtained x 100 theoretical yield of product

15. 0 g C 3 H 8 was combusted with 15. 0 g O 2. How many g of H 2 O are theoretically possible ? 1. Write the rxn and balance it 2. Calculate theoretical yield starting with each reactant. The smallest value obtained is theoretical yield and is thus the one based on the limiting reagent

15. 0 g C 3 H 8 was combusted with 15. 0 g O 2 and 5. 84 g H 2 O is obtained. What is the %yield of H 2 O ?