Formula for Linear Regression Slope or the change

Formula for Linear Regression Slope or the change in y for every unit change in x Y-intercept or the value of y when x = 0. y = bx + a Y variable plotted on vertical axis. X variable plotted on horizontal axis.

Interpretation of parameters • The regression slope is the average change in Y when X increases by 1 unit • The intercept is the predicted value for Y when X = 0 • If the slope = 0, then X does not help in predicting Y (linearly)

General ANOVA Setting Comparisons of 2 or more means • Investigator controls one or more independent variables – Called factors (or treatment variables) – Each factor contains two or more levels (or groups or categories/classifications) • Observe effects on the dependent variable – Response to levels of independent variable • Experimental design: the plan used to collect the data

Logic of ANOVA • Each observation Mean is different from the Grand (total sample) Mean by some amount • There are two sources of variance from the mean: – 1) That due to the treatment or independent variable – 2) That which is unexplained by our treatment

One-Way Analysis of Variance • Evaluate the difference among the means of two or more groups Examples: Accident rates for 1 st, 2 nd, and 3 rd shift Expected mileage for five brands of tires • Assumptions – Populations are normally distributed – Populations have equal variances – Samples are randomly and independently drawn

Hypotheses of One-Way ANOVA - All population means are equal - i. e. , no treatment effect (no variation in means among groups) - At least one population mean is different - i. e. , there is a treatment effect - Does not mean that all population means are different (some pairs may be the same) - ANOVA does not tell you where the difference lies. For this reason , you need another test, either the Scheffe' or Tukey post ANOVA test.

One-Factor ANOVA All Means are the same: The Null Hypothesis is True (No Treatment Effect)

One-Factor ANOVA (continued) At least one mean is different: The Null Hypothesis is NOT true (Treatment Effect is present) or

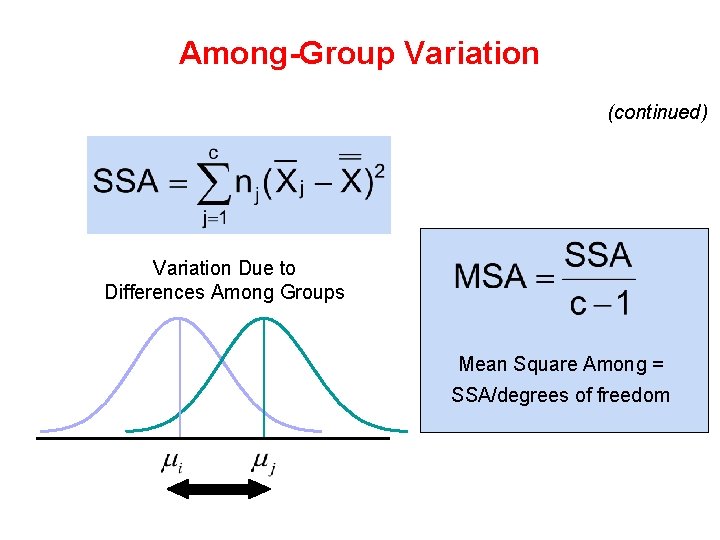
Partitioning the Variation • Total variation can be split into two parts: SST = SSA + SSW SST = Total Sum of Squares (Total variation) SSA = Sum of Squares Among Groups (Among-group variation) SSW = Sum of Squares Within Groups (Within-group variation)

Partitioning the Variation (continued) SST = SSA + SSW Total Variation = the aggregate dispersion of the individual data values across the various factor levels (SST) Among-Group Variation = dispersion between the factor sample means (SSA) Within-Group Variation = dispersion that exists among the data values within a particular factor level (SSW)

Partition of Total Variation (SST) d. f. = n – 1 = Variation Due to Factor (SSA) + Variation Due to Random Sampling (SSW) d. f. = c – 1 § § Commonly referred to as: Sum of Squares Between Sum of Squares Among Sum of Squares Explained Among Groups Variation d. f. = n – c § § Commonly referred to as: Sum of Squares Within Sum of Squares Error Sum of Squares Unexplained Within-Group Variation

Among-Group Variation (continued) Variation Due to Differences Among Groups Mean Square Among = SSA/degrees of freedom

Within-Group Variation (continued) Summing the variation within each group and then adding over all groups Mean Square Within = SSW/degrees of freedom

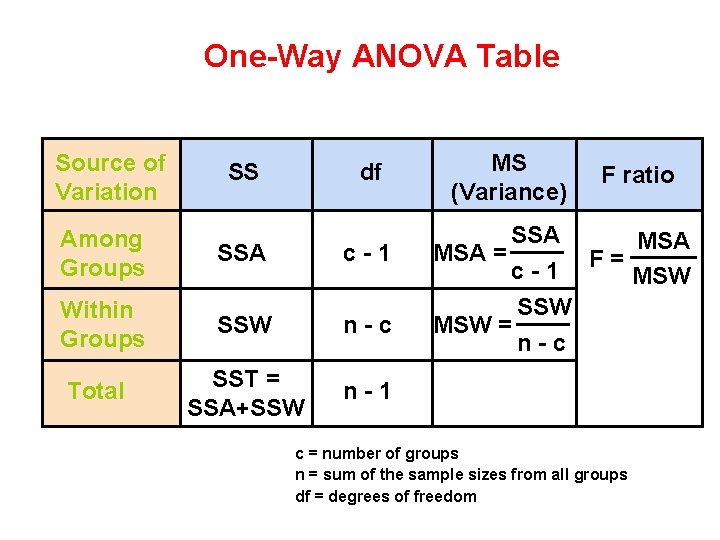
One-Way ANOVA Table Source of Variation SS df Among Groups SSA c-1 Within Groups SSW n-c Total SST = SSA+SSW n-1 MS (Variance) F ratio SSA MSA = c - 1 F = MSW SSW MSW = n-c c = number of groups n = sum of the sample sizes from all groups df = degrees of freedom

One-Way ANOVA: F Test Statistic H 0: μ 1= μ 2 = … = μ c H 1: At least two population means are different • Test statistic MSA is mean squares among groups MSW is mean squares within groups • Degrees of freedom – df 1 = c – 1 – df 2 = n – c (c = number of groups) (n = sum of sample sizes from all populations)

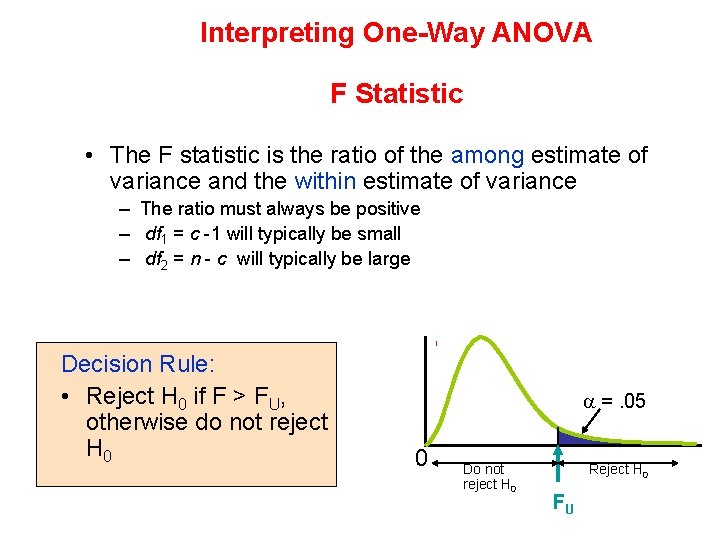
Interpreting One-Way ANOVA F Statistic • The F statistic is the ratio of the among estimate of variance and the within estimate of variance – The ratio must always be positive – df 1 = c -1 will typically be small – df 2 = n - c will typically be large Decision Rule: • Reject H 0 if F > FU, otherwise do not reject H 0 =. 05 0 Do not reject H 0 Reject H 0 FU

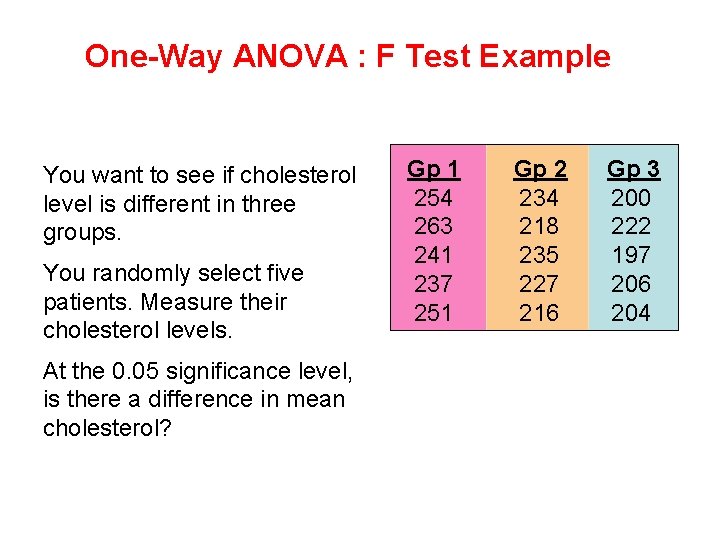
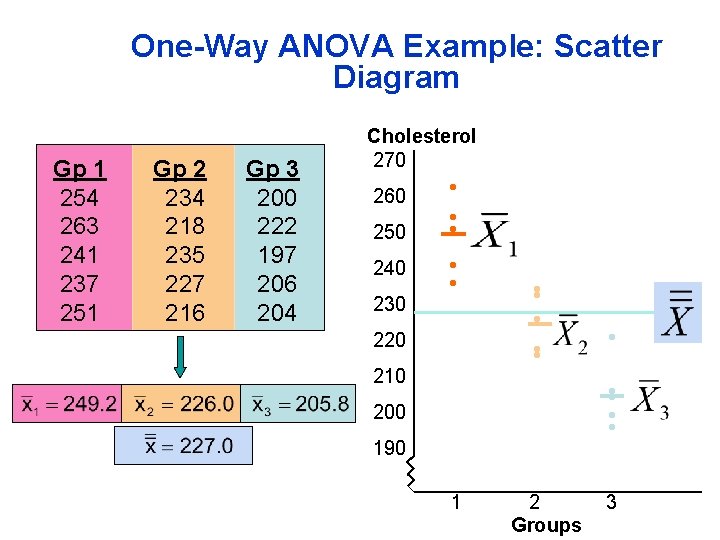
One-Way ANOVA : F Test Example You want to see if cholesterol level is different in three groups. You randomly select five patients. Measure their cholesterol levels. At the 0. 05 significance level, is there a difference in mean cholesterol? Gp 1 254 263 241 237 251 Gp 2 234 218 235 227 216 Gp 3 200 222 197 206 204

One-Way ANOVA Example: Scatter Diagram Gp 1 254 263 241 237 251 Gp 2 234 218 235 227 216 Gp 3 200 222 197 206 204 Cholesterol 270 260 250 240 230 • • • 220 210 • • • • • 200 190 1 2 Groups 3

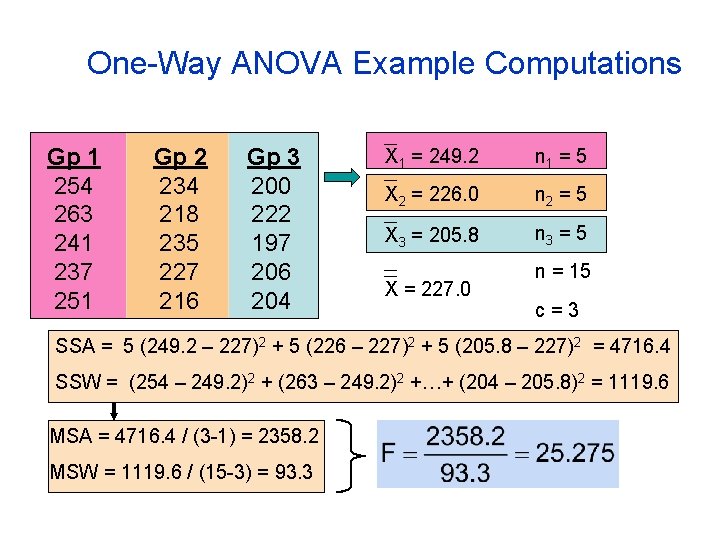
One-Way ANOVA Example Computations Gp 1 254 263 241 237 251 Gp 2 234 218 235 227 216 Gp 3 200 222 197 206 204 X 1 = 249. 2 n 1 = 5 X 2 = 226. 0 n 2 = 5 X 3 = 205. 8 n 3 = 5 X = 227. 0 n = 15 c=3 SSA = 5 (249. 2 – 227)2 + 5 (226 – 227)2 + 5 (205. 8 – 227)2 = 4716. 4 SSW = (254 – 249. 2)2 + (263 – 249. 2)2 +…+ (204 – 205. 8)2 = 1119. 6 MSA = 4716. 4 / (3 -1) = 2358. 2 MSW = 1119. 6 / (15 -3) = 93. 3

One-Way ANOVA Example Solution H 0: μ 1 = μ 2 = μ 3 H 1: μj not all equal Test Statistic: = 0. 05 df 1= 2 df 2 = 12 Critical Value: FU = 3. 89 =. 05 0 Do not reject H 0 Reject H 0 FU = 3. 89 Decision: Reject H 0 at = 0. 05 Conclusion: There is evidence that at least one μj differs F = 25. 275 from the rest

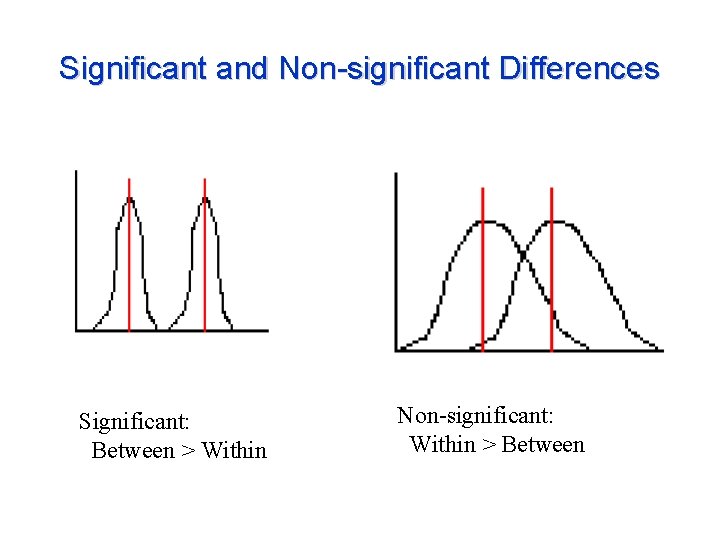
Significant and Non-significant Differences Significant: Between > Within Non-significant: Within > Between

ANOVA (summary) §Null hypothesis is that there is no difference between the means. §Alternate hypothesis is that at least two means differ. §Use the F statistic as your test statistic. It tests the between-sample variance (difference between the means) against the within-sample variance (variability within the sample). The larger this is the more likely the means are different. §Degrees of freedom for numerator is k-1 (k is the number of treatments) §Degrees of freedom for the denominator is n-k (n is the number of responses) §If test F is larger than critical F, then reject the null. §If p-value is less than alpha, then reject the null.

ANOVA (summary) WHEN YOU REJECT THE NULL For an one-way ANOVA after you have rejected the null, you may want to determine which treatment yielded the best results. Must do follow-on analysis to determine if the difference between each pair of means if significant (post ANOVA test).

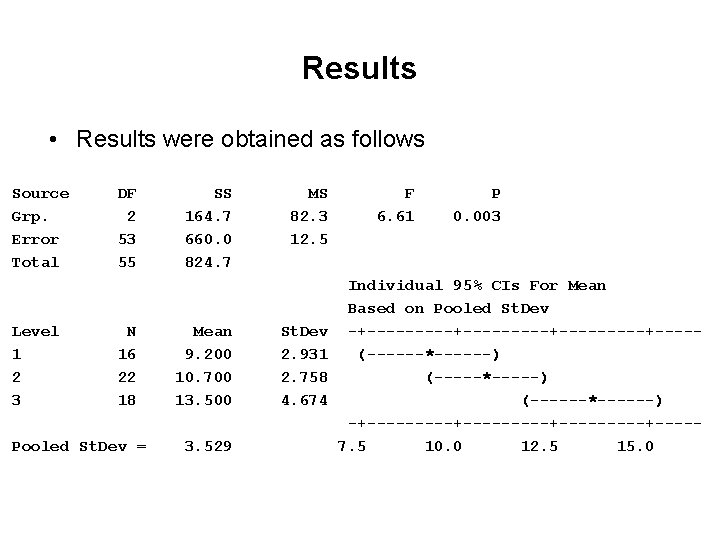
One-way ANOVA (example) The study described here is about measuring cortisol levels in 3 groups of subjects : • Healthy (n = 16) • Depressed: Non-melancholic depressed (n = 22) • Depressed: Melancholic depressed (n = 18)

Results • Results were obtained as follows Source Grp. Error Total Level 1 2 3 DF 2 53 55 N 16 22 18 Pooled St. Dev = SS 164. 7 660. 0 824. 7 Mean 9. 200 10. 700 13. 500 3. 529 MS 82. 3 12. 5 St. Dev 2. 931 2. 758 4. 674 F 6. 61 P 0. 003 Individual 95% CIs For Mean Based on Pooled St. Dev -+---------+-----+----(------*------) (-----*-----) (------*------) -+---------+-----+----7. 5 10. 0 12. 5 15. 0

Multiple Comparison of the Means - 1 • Several methods are available depending upon whether one wishes to compare means with a control mean (Dunnett) or just overall comparison (Tukey and Fisher) Dunnett's comparisons with a control Critical value = 2. 27 Control = level (1) of Grp. Intervals for treatment mean minus control mean Level Lower Center Upper -----+---------+-----+- • 2 -1. 127 1. 500 4. 127 (-----*-----) • 3 1. 553 4. 300 7. 047 (-----*-----) • -----+---------+-----+--1. 0 1. 5 4. 0 7. 0

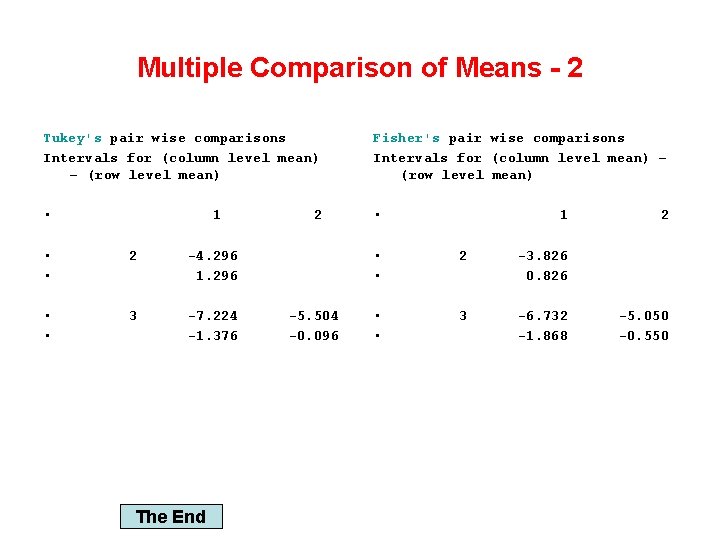
Multiple Comparison of Means - 2 Tukey's pair wise comparisons Intervals for (column level mean) − (row level mean) Fisher's pair wise comparisons Intervals for (column level mean) − (row level mean) • • 1 • • 2 -4. 296 1. 296 • • 3 -7. 224 -1. 376 The End 2 -5. 504 -0. 096 1 • • 2 -3. 826 0. 826 • • 3 -6. 732 -1. 868 2 -5. 050 -0. 550