FORMATION AND EVOLUTION OF DEFECTS IN MATERIALS OF

FORMATION AND EVOLUTION OF DEFECTS IN MATERIALS OF INTEREST FOR FUSION CHRISTOPHE J. ORTIZ (PERMANENT STAFF) CARLO GUERRERO (POST-DOC, M 4 F PROJECT) GONZALO VALLES ALBERDI (POST-DOC, EUROFUSION ENGINEERING GRANT) FERNANDO JIMENEZ PIÑERO (PHD STUDENT, EFDA-GOT PROJECT) LABORATORIO NACIONAL DE FUSIÓN POR CONFINAMIENTO MAGNÉTICO – CIEMAT, MADRID, SPAIN www. kit. edu

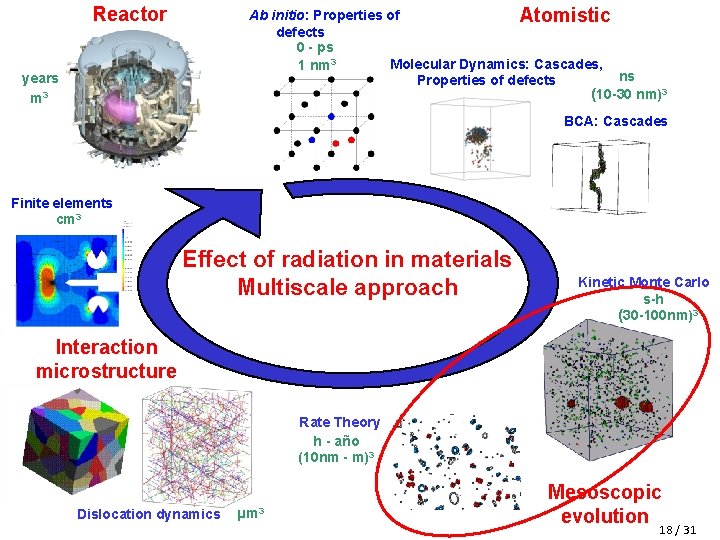
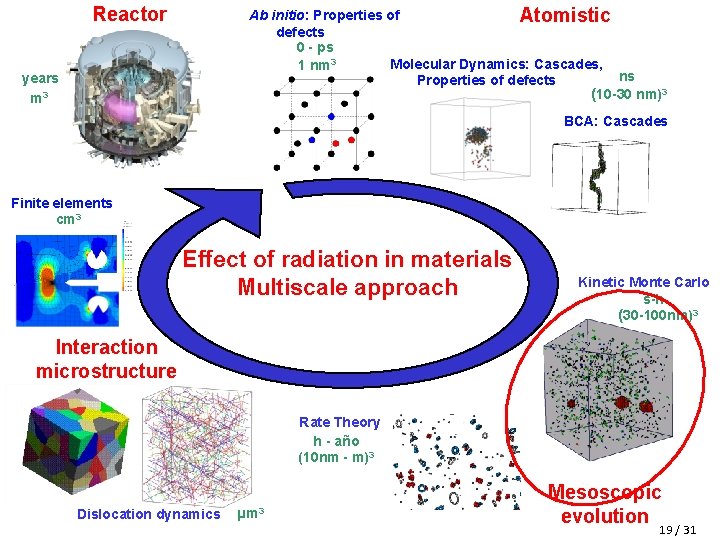
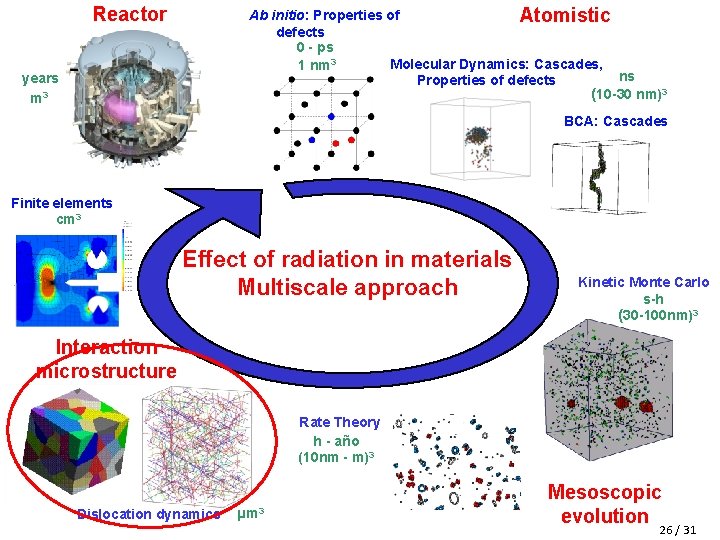
Effect of radiation in candidate materials for future fusion reactors Modification of material Interaction defects - microstructure properties Collision cascade Atomistic fs-ps / nm 3 Micro-Macro µm 3 – cm 3 Swelling Embrittlement Nucleation/Growth of defects Mesoscopic ns - year / nm 3 - µm 3 § In fusion conditions, energetic neutrons (~14 Me. V) will displace lattice atoms (Primary Knock. On Atoms) in the material by collisions with nuclei, which triggers a collision cascade (nm 3, ps). § Defects formed during collision cascades then diffuse for long time (s-years), can agglomerate and interact with the microstructure, which alters the macroscopic properties of materials. § The problem of radiation damage is multiscale by nature. 2 / 31

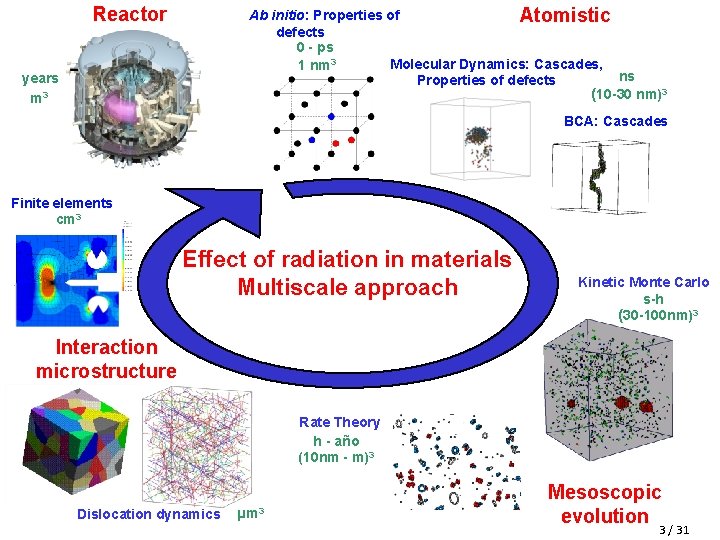
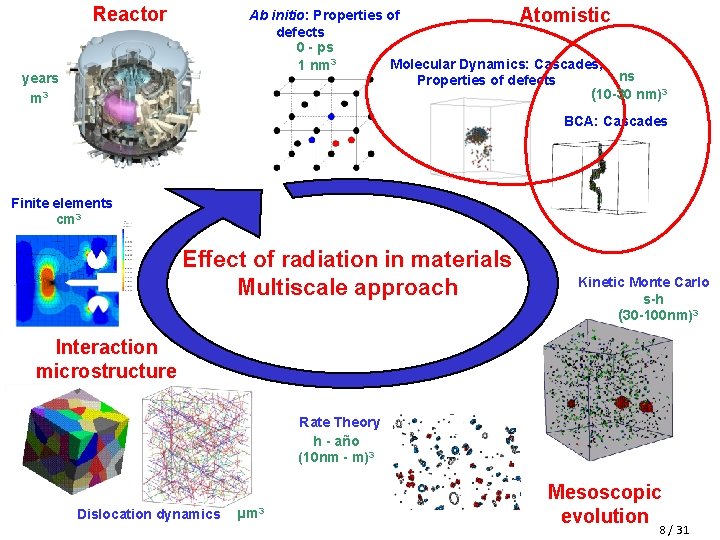
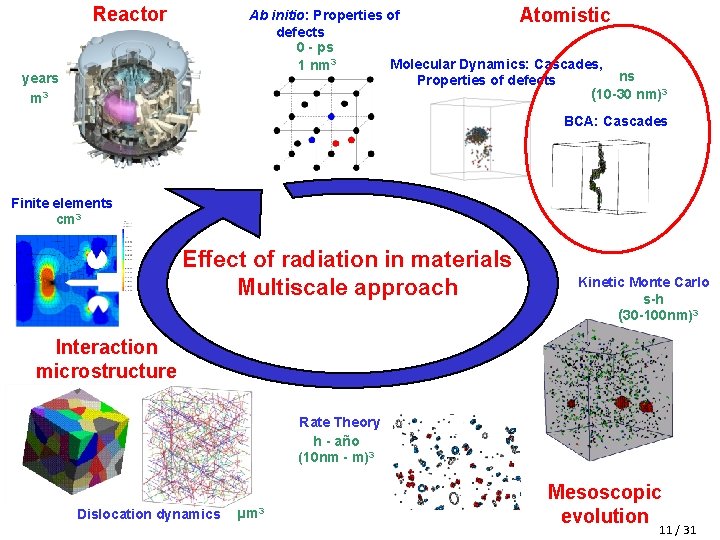
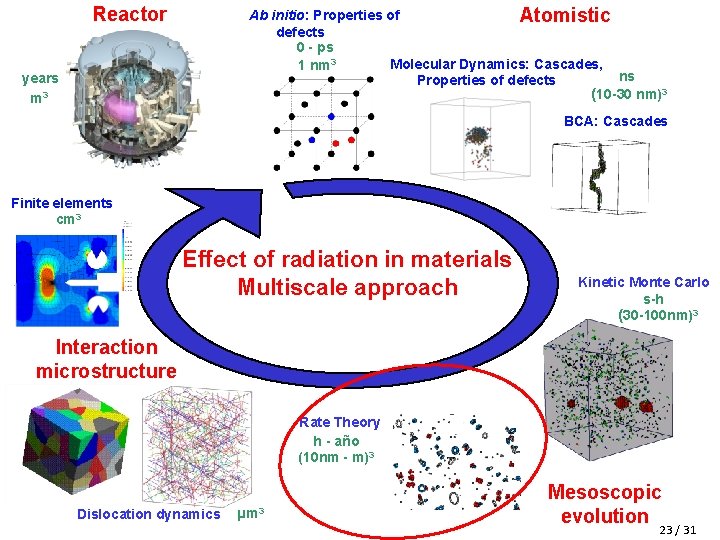
Reactor Ab initio: Properties of Atomistic defects 0 - ps Molecular Dynamics: Cascades, 1 nm 3 ns Properties of defects (10 -30 nm)3 years m 3 BCA: Cascades Finite elements cm 3 Effect of radiation in materials Multiscale approach Kinetic Monte Carlo s-h (30 -100 nm)3 Interaction microstructure Rate Theory h - año (10 nm - m)3 Dislocation dynamics µm 3 Mesoscopic evolution 3 / 31

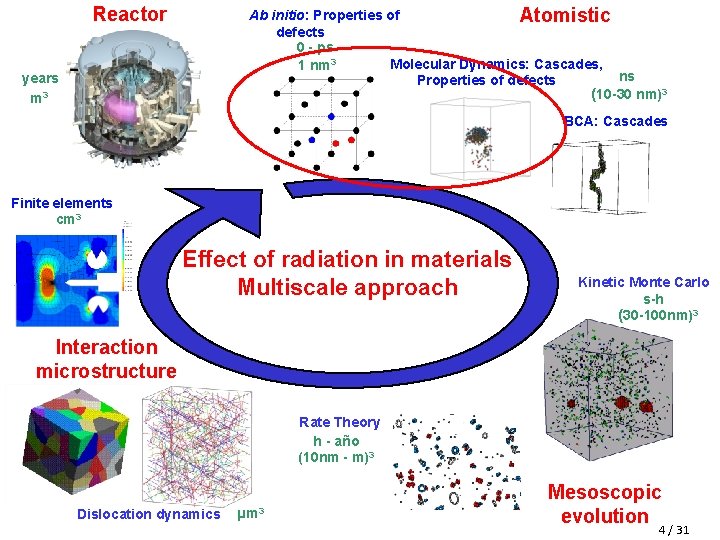
Reactor Ab initio: Properties of Atomistic defects 0 - ps Molecular Dynamics: Cascades, 1 nm 3 ns Properties of defects (10 -30 nm)3 years m 3 BCA: Cascades Finite elements cm 3 Effect of radiation in materials Multiscale approach Kinetic Monte Carlo s-h (30 -100 nm)3 Interaction microstructure Rate Theory h - año (10 nm - m)3 Dislocation dynamics µm 3 Mesoscopic evolution 4 / 31

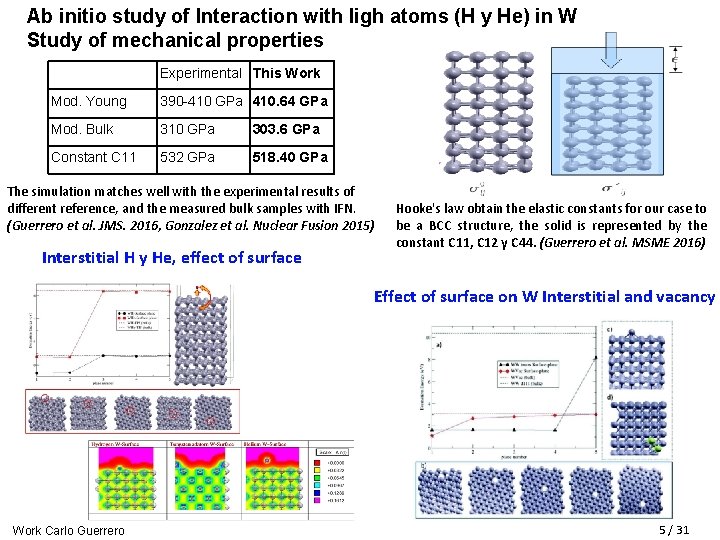
Ab initio study of Interaction with ligh atoms (H y He) in W Study of mechanical properties Experimental This Work Mod. Young 390 -410 GPa 410. 64 GPa Mod. Bulk 310 GPa 303. 6 GPa Constant C 11 532 GPa 518. 40 GPa The simulation matches well with the experimental results of different reference, and the measured bulk samples with IFN. (Guerrero et al. JMS. 2016, Gonzalez et al. Nuclear Fusion 2015) Interstitial H y He, effect of surface Hooke's law obtain the elastic constants for our case to be a BCC structure, the solid is represented by the constant C 11, C 12 y C 44. (Guerrero et al. MSME 2016) Effect of surface on W Interstitial and vacancy Work Carlo Guerrero 5 / 31

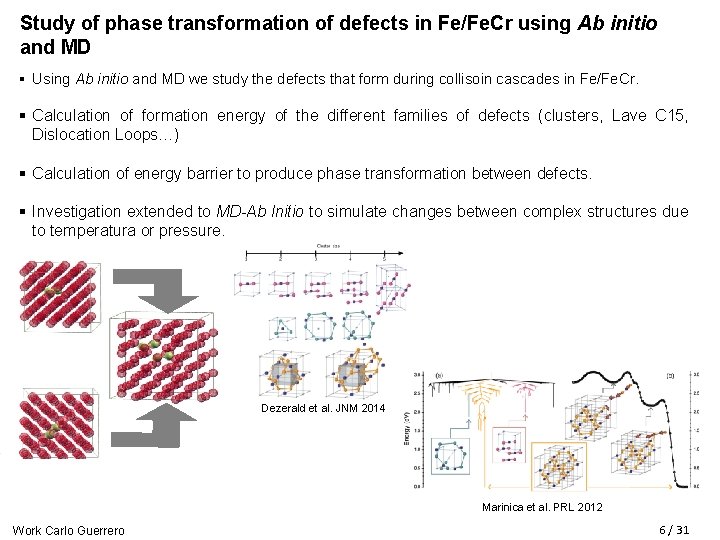
Study of phase transformation of defects in Fe/Fe. Cr using Ab initio and MD § Using Ab initio and MD we study the defects that form during collisoin cascades in Fe/Fe. Cr. § Calculation of formation energy of the different families of defects (clusters, Lave C 15, Dislocation Loops…) § Calculation of energy barrier to produce phase transformation between defects. § Investigation extended to MD-Ab Initio to simulate changes between complex structures due to temperatura or pressure. Dezerald et al. JNM 2014 Marinica et al. PRL 2012 Work Carlo Guerrero 6 / 31

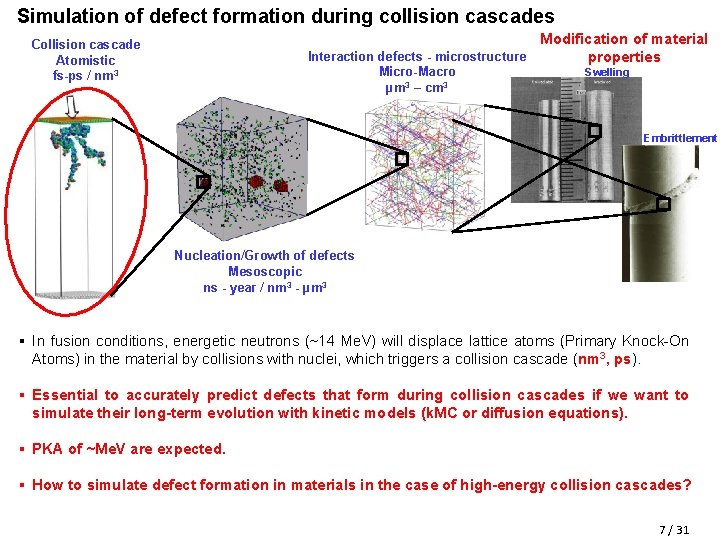
Simulation of defect formation during collision cascades Modification of material Interaction defects - microstructure properties Collision cascade Atomistic fs-ps / nm 3 Micro-Macro µm 3 – cm 3 Swelling Embrittlement Nucleation/Growth of defects Mesoscopic ns - year / nm 3 - µm 3 § In fusion conditions, energetic neutrons (~14 Me. V) will displace lattice atoms (Primary Knock-On Atoms) in the material by collisions with nuclei, which triggers a collision cascade (nm 3, ps). § Essential to accurately predict defects that form during collision cascades if we want to simulate their long-term evolution with kinetic models (k. MC or diffusion equations). § PKA of ~Me. V are expected. § How to simulate defect formation in materials in the case of high-energy collision cascades? 7 / 31

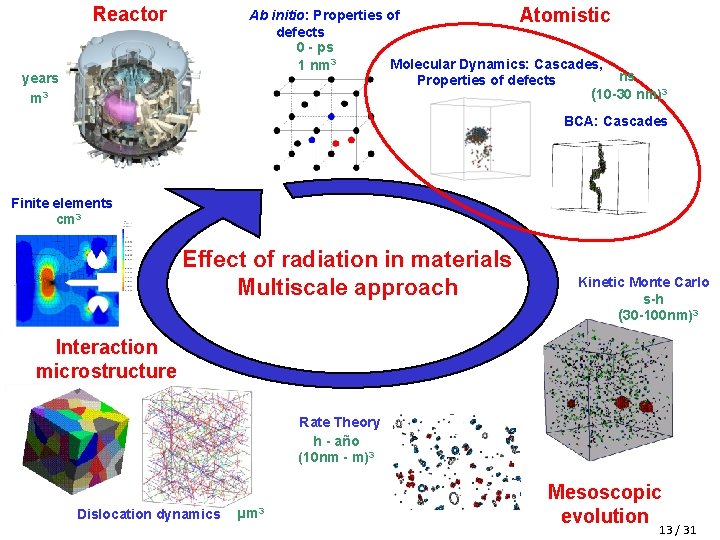
Reactor Ab initio: Properties of Atomistic defects 0 - ps Molecular Dynamics: Cascades, 1 nm 3 ns Properties of defects (10 -30 nm)3 years m 3 BCA: Cascades Finite elements cm 3 Effect of radiation in materials Multiscale approach Kinetic Monte Carlo s-h (30 -100 nm)3 Interaction microstructure Rate Theory h - año (10 nm - m)3 Dislocation dynamics µm 3 Mesoscopic evolution 8 / 31

Reactor Ab initio: Properties of Atomistic defects 0 - ps Molecular Dynamics: Cascades, 1 nm 3 ns Properties of defects (10 -30 nm)3 years m 3 BCA: Cascades Finite elements cm 3 Effect of radiation in materials Multiscale approach Kinetic Monte Carlo s-h (30 -100 nm)3 Interaction microstructure Rate Theory h - año (10 nm - m)3 Dislocation dynamics µm 3 Mesoscopic evolution 9 / 31

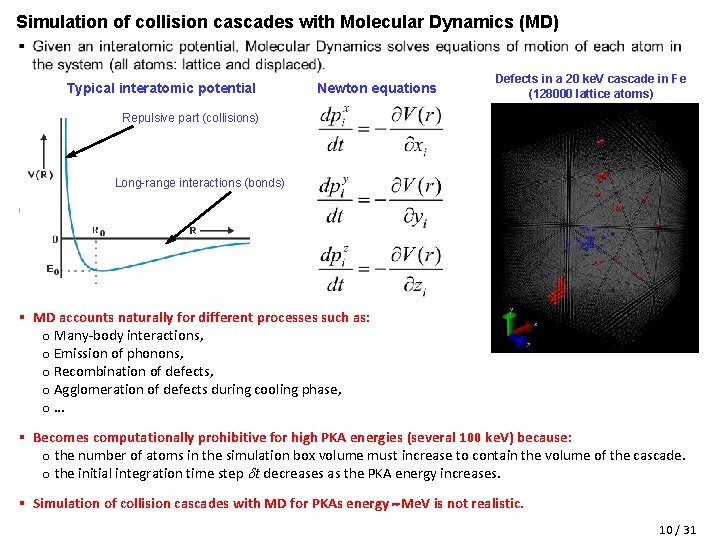
Simulation of collision cascades with Molecular Dynamics (MD) Typical interatomic potential Newton equations Defects in a 20 ke. V cascade in Fe (128000 lattice atoms) Repulsive part (collisions) Long-range interactions (bonds) § MD accounts naturally for different processes such as: o Many-body interactions, o Emission of phonons, o Recombination of defects, o Agglomeration of defects during cooling phase, o… § Becomes computationally prohibitive for high PKA energies (several 100 ke. V) because: o the number of atoms in the simulation box volume must increase to contain the volume of the cascade. o the initial integration time step t decreases as the PKA energy increases. § Simulation of collision cascades with MD for PKAs energy Me. V is not realistic. 10 / 31

Reactor Ab initio: Properties of Atomistic defects 0 - ps Molecular Dynamics: Cascades, 1 nm 3 ns Properties of defects (10 -30 nm)3 years m 3 BCA: Cascades Finite elements cm 3 Effect of radiation in materials Multiscale approach Kinetic Monte Carlo s-h (30 -100 nm)3 Interaction microstructure Rate Theory h - año (10 nm - m)3 Dislocation dynamics µm 3 Mesoscopic evolution 11 / 31

Simulation of collision cascades with Binary Collision Approximation (BCA) § Given a repulsive interatomic potential (collision part), the collision problem can be reduced to binary collisions if Eprojectile Etarget. § Between two collisions, the trajectroy of particles is approximated as independent rectilinear segments. Typical interatomic potential Representation of a binary collision Repulsive part (collisions) Ef Projectile, Ei b: impact param. Target T § Very fast simulations (s-min on a PC) since only atoms that are displaced are taken into account in the calculations (not lattice atoms like MD). § Drawbacks of BCA: o o Breaks down when velocity of projectile is low (Vprojectile Vsound) in the material. Simultaneous collisions not properly taken into account. Does not take into account long-range interactions between atoms. Cannot account for cluster formation or recombination of defects during last stages of the cascade. § BCA not able to correctly simulate last stages of collision cascades and defects (number, configuration, size) that survive collision cascades. 12 / 31

Reactor Ab initio: Properties of Atomistic defects 0 - ps Molecular Dynamics: Cascades, 1 nm 3 ns Properties of defects (10 -30 nm)3 years m 3 BCA: Cascades Finite elements cm 3 Effect of radiation in materials Multiscale approach Kinetic Monte Carlo s-h (30 -100 nm)3 Interaction microstructure Rate Theory h - año (10 nm - m)3 Dislocation dynamics µm 3 Mesoscopic evolution 13 / 31

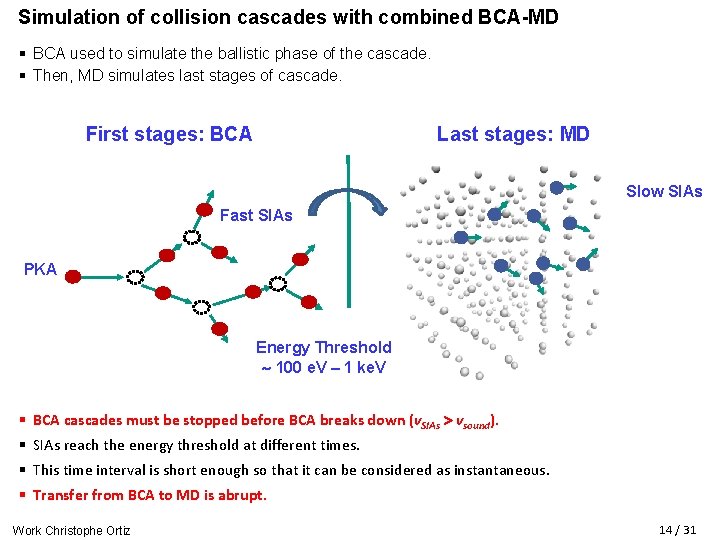
Simulation of collision cascades with combined BCA-MD § BCA used to simulate the ballistic phase of the cascade. § Then, MD simulates last stages of cascade. First stages: BCA Last stages: MD Slow SIAs Fast SIAs PKA Energy Threshold 100 e. V – 1 ke. V § BCA cascades must be stopped before BCA breaks down (v. SIAs vsound). § SIAs reach the energy threshold at different times. § This time interval is short enough so that it can be considered as instantaneous. § Transfer from BCA to MD is abrupt. Work Christophe Ortiz 14 / 31

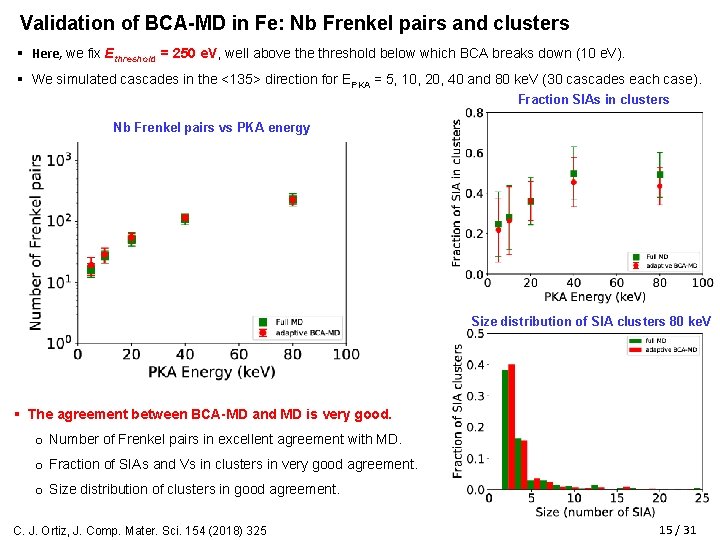
Validation of BCA-MD in Fe: Nb Frenkel pairs and clusters § Here, we fix Ethreshold = 250 e. V, well above threshold below which BCA breaks down (10 e. V). § We simulated cascades in the <135> direction for EPKA = 5, 10, 20, 40 and 80 ke. V (30 cascades each case). Fraction SIAs in clusters Nb Frenkel pairs vs PKA energy Size distribution of SIA clusters 80 ke. V § The agreement between BCA-MD and MD is very good. o Number of Frenkel pairs in excellent agreement with MD. o Fraction of SIAs and Vs in clusters in very good agreement. o Size distribution of clusters in good agreement. 325 C. J. Ortiz, J. Comp. Mater. Sci. 154 (2018) 15 / 31

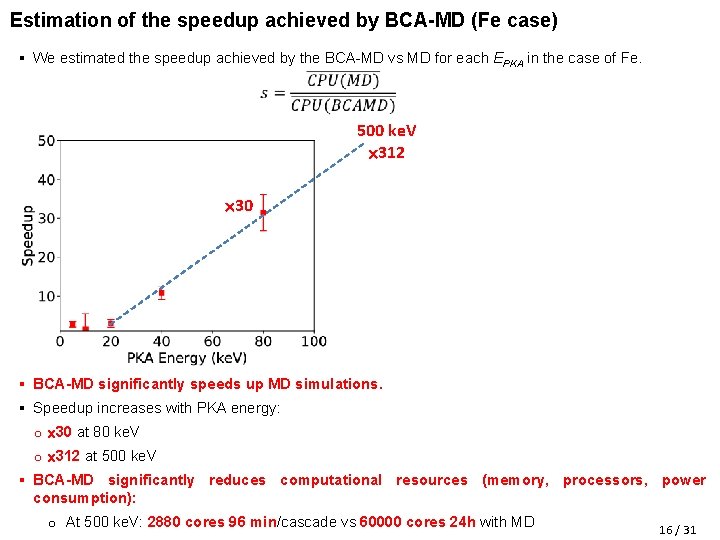
Estimation of the speedup achieved by BCA-MD (Fe case) § We estimated the speedup achieved by the BCA-MD vs MD for each EPKA in the case of Fe. 500 ke. V 312 30 § BCA-MD significantly speeds up MD simulations. § Speedup increases with PKA energy: o 30 at 80 ke. V o 312 at 500 ke. V § BCA-MD significantly reduces computational resources (memory, processors, power consumption): o At 500 ke. V: 2880 cores 96 min/cascade vs 60000 cores 24 h with MD 16 / 31

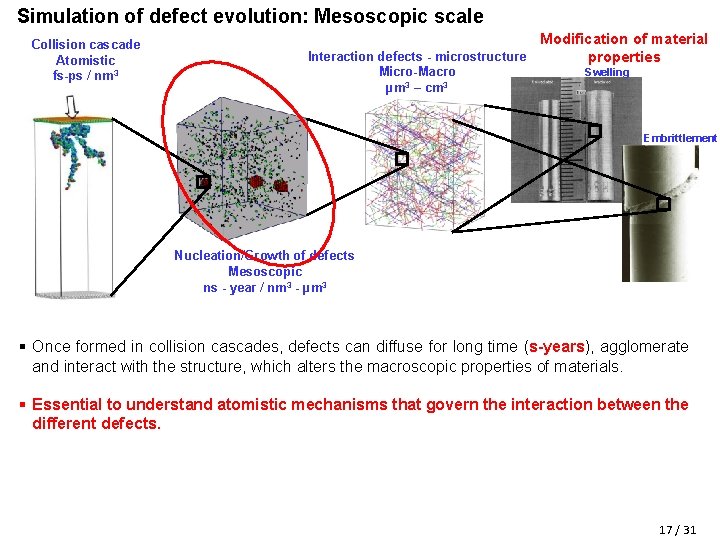
Simulation of defect evolution: Mesoscopic scale Modification of material Interaction defects - microstructure properties Collision cascade Atomistic fs-ps / nm 3 Micro-Macro µm 3 – cm 3 Swelling Embrittlement Nucleation/Growth of defects Mesoscopic ns - year / nm 3 - µm 3 § Once formed in collision cascades, defects can diffuse for long time (s-years), agglomerate and interact with the structure, which alters the macroscopic properties of materials. § Essential to understand atomistic mechanisms that govern the interaction between the different defects. 17 / 31

Reactor Ab initio: Properties of Atomistic defects 0 - ps Molecular Dynamics: Cascades, 1 nm 3 ns Properties of defects (10 -30 nm)3 years m 3 BCA: Cascades Finite elements cm 3 Effect of radiation in materials Multiscale approach Kinetic Monte Carlo s-h (30 -100 nm)3 Interaction microstructure Rate Theory h - año (10 nm - m)3 Dislocation dynamics µm 3 Mesoscopic evolution 18 / 31

Reactor Ab initio: Properties of Atomistic defects 0 - ps Molecular Dynamics: Cascades, 1 nm 3 ns Properties of defects (10 -30 nm)3 years m 3 BCA: Cascades Finite elements cm 3 Effect of radiation in materials Multiscale approach Kinetic Monte Carlo s-h (30 -100 nm)3 Interaction microstructure Rate Theory h - año (10 nm - m)3 Dislocation dynamics µm 3 Mesoscopic evolution 19 / 31

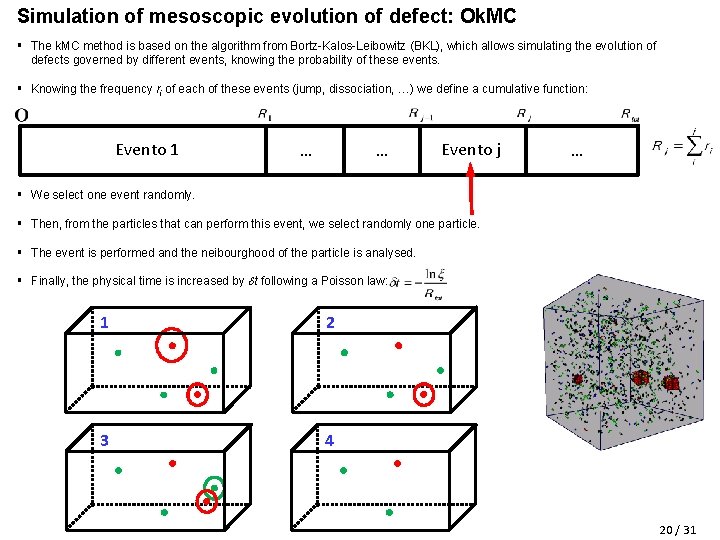
Simulation of mesoscopic evolution of defect: Ok. MC § The k. MC method is based on the algorithm from Bortz-Kalos-Leibowitz (BKL), which allows simulating the evolution of defects governed by different events, knowing the probability of these events. § Knowing the frequency ri of each of these events (jump, dissociation, …) we define a cumulative function: Evento 1 … … Evento j … § We select one event randomly. § Then, from the particles that can perform this event, we select randomly one particle. § The event is performed and the neibourghood of the particle is analysed. § Finally, the physical time is increased by t following a Poisson law: 1 2 3 4 20 / 31

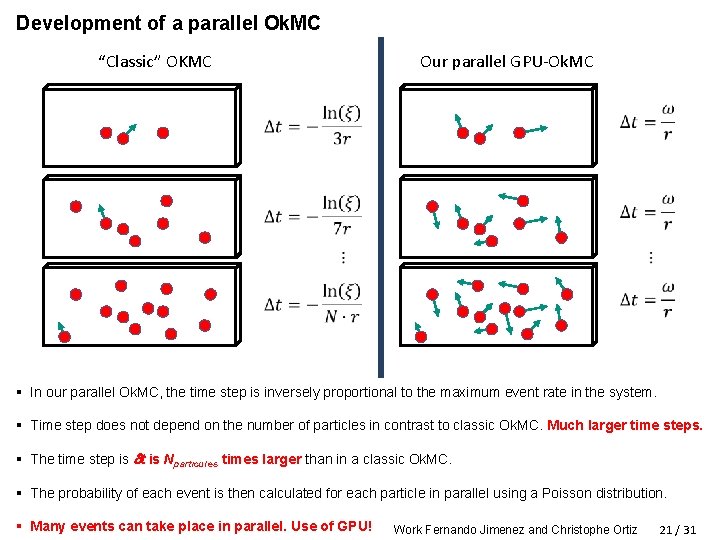
Development of a parallel Ok. MC Our parallel GPU-Ok. MC “Classic” OKMC § In our parallel Ok. MC, the time step is inversely proportional to the maximum event rate in the system. § Time step does not depend on the number of particles in contrast to classic Ok. MC. Much larger time steps. § The time step is t is Nparticules times larger than in a classic Ok. MC. § The probability of each event is then calculated for each particle in parallel using a Poisson distribution. § Many events can take place in parallel. Use of GPU! Work Fernando Jimenez and Christophe Ortiz 21 / 31

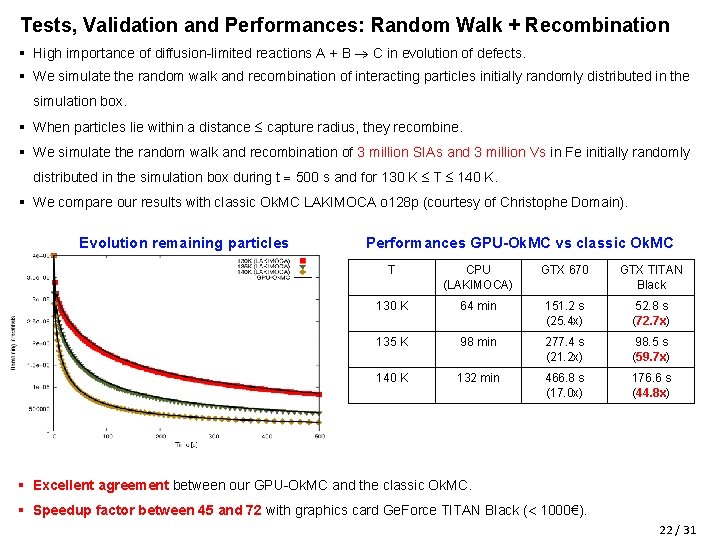
Tests, Validation and Performances: Random Walk + Recombination § High importance of diffusion-limited reactions A + B C in evolution of defects. § We simulate the random walk and recombination of interacting particles initially randomly distributed in the simulation box. § When particles lie within a distance capture radius, they recombine. § We simulate the random walk and recombination of 3 million SIAs and 3 million Vs in Fe initially randomly distributed in the simulation box during t 500 s and for 130 K T 140 K. § We compare our results with classic Ok. MC LAKIMOCA o 128 p (courtesy of Christophe Domain). Performances GPU-Ok. MC vs classic Ok. MC Evolution remaining particles T CPU (LAKIMOCA) GTX 670 GTX TITAN Black 130 K 64 min 151. 2 s (25. 4 x) 52. 8 s (72. 7 x) 135 K 98 min 277. 4 s (21. 2 x) 98. 5 s (59. 7 x) 140 K 132 min 466. 8 s (17. 0 x) 176. 6 s (44. 8 x) § Excellent agreement between our GPU-Ok. MC and the classic Ok. MC. § Speedup factor between 45 and 72 with graphics card Ge. Force TITAN Black ( 1000€). 22 / 31

Reactor Ab initio: Properties of Atomistic defects 0 - ps Molecular Dynamics: Cascades, 1 nm 3 ns Properties of defects (10 -30 nm)3 years m 3 BCA: Cascades Finite elements cm 3 Effect of radiation in materials Multiscale approach Kinetic Monte Carlo s-h (30 -100 nm)3 Interaction microstructure Rate Theory h - año (10 nm - m)3 Dislocation dynamics µm 3 Mesoscopic evolution 23 / 31

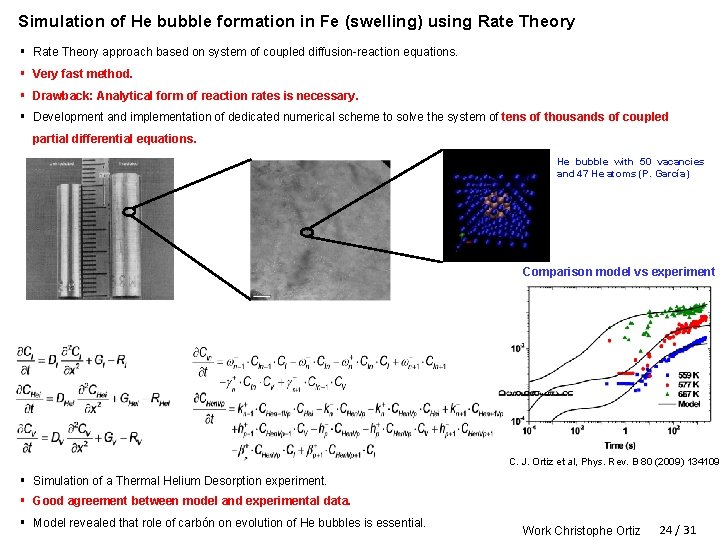
Simulation of He bubble formation in Fe (swelling) using Rate Theory § Rate Theory approach based on system of coupled diffusion-reaction equations. § Very fast method. § Drawback: Analytical form of reaction rates is necessary. § Development and implementation of dedicated numerical scheme to solve the system of tens of thousands of coupled partial differential equations. He bubble with 50 vacancies and 47 He atoms (P. García) Comparison model vs experiment C. J. Ortiz et al, Phys. Rev. B 80 (2009) 134109 § Simulation of a Thermal Helium Desorption experiment. § Good agreement between model and experimental data. § Model revealed that role of carbón on evolution of He bubbles is essential. Work Christophe Ortiz 24 / 31

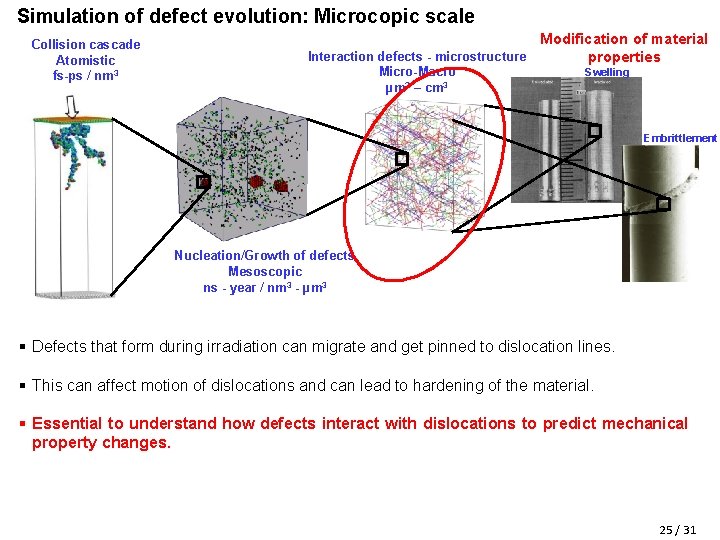
Simulation of defect evolution: Microcopic scale Modification of material Interaction defects - microstructure properties Collision cascade Atomistic fs-ps / nm 3 Micro-Macro µm 3 – cm 3 Swelling Embrittlement Nucleation/Growth of defects Mesoscopic ns - year / nm 3 - µm 3 § Defects that form during irradiation can migrate and get pinned to dislocation lines. § This can affect motion of dislocations and can lead to hardening of the material. § Essential to understand how defects interact with dislocations to predict mechanical property changes. 25 / 31

Reactor Ab initio: Properties of Atomistic defects 0 - ps Molecular Dynamics: Cascades, 1 nm 3 ns Properties of defects (10 -30 nm)3 years m 3 BCA: Cascades Finite elements cm 3 Effect of radiation in materials Multiscale approach Kinetic Monte Carlo s-h (30 -100 nm)3 Interaction microstructure Rate Theory h - año (10 nm - m)3 Dislocation dynamics µm 3 Mesoscopic evolution 26 / 31

Dislocation Dynamics (DD) § To investigate the influence of defects on the plastic response of the irradiated materials we can use the Dislocation Dynamics. § The Dislocation Dynamics: o Calculates the elastic interaction between dislocation segments o Takes into account interaction defect/dislocation o Tracks the plastic response immediately after the yield § To investigate the influence of defects on mechanical properties, we use MODELib (Mechanics Of Defect Evolution Library) § Works in FCC, BCC, HCP § Allows to set microstructure o Dislocation distribution o Defect distribution § Allows to simulate strain-stress curve § Limited to 1 grain and to small strains Work Gonzalo Valles [1] Y. Cui et al. PRL 120 (2018) 215501 [2] Amodeo and Ghoniem. PRB 41 (1990) 6958 -6967 [3] Ghoniem et al. PRB 61 (2000) 913 -927 [4] Po and Ghoniem. J. Mech. Phys. Solids 66 (2014) 103 -116 27 / 31

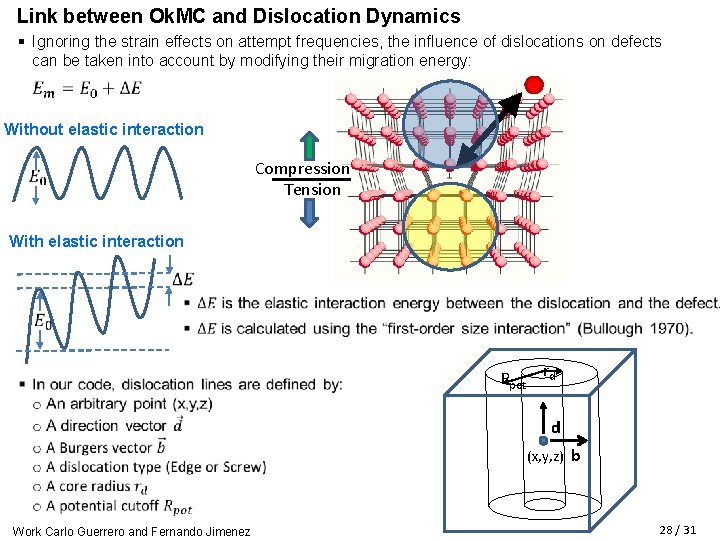
Link between Ok. MC and Dislocation Dynamics § Ignoring the strain effects on attempt frequencies, the influence of dislocations on defects can be taken into account by modifying their migration energy: Without elastic interaction Compression Tension With elastic interaction Rpot rd d (x, y, z) Work Carlo Guerrero and Fernando Jimenez b 28 / 31

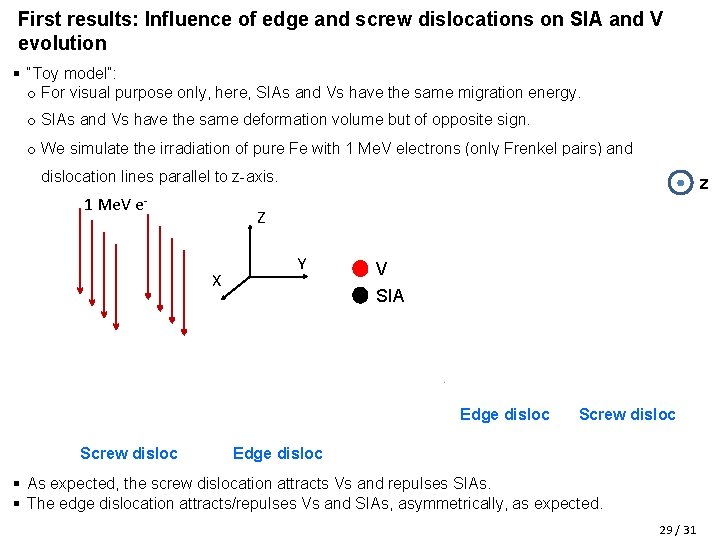
First results: Influence of edge and screw dislocations on SIA and V evolution § “Toy model”: o For visual purpose only, here, SIAs and Vs have the same migration energy. o SIAs and Vs have the same deformation volume but of opposite sign. o We simulate the irradiation of pure Fe with 1 Me. V electrons (only Frenkel pairs) and dislocation lines parallel to z-axis. 1 Me. V e- z Z Y X V SIA Edge disloc Screw disloc Edge disloc § As expected, the screw dislocation attracts Vs and repulses SIAs. § The edge dislocation attracts/repulses Vs and SIAs, asymmetrically, as expected. 29 / 31

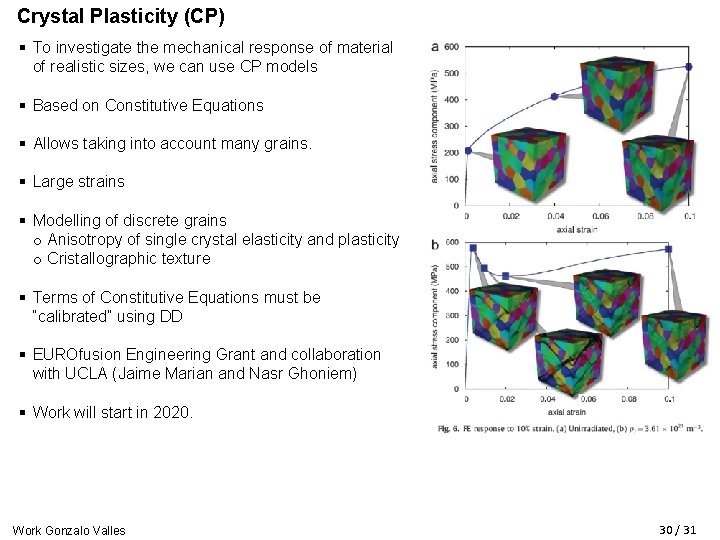
Crystal Plasticity (CP) § To investigate the mechanical response of material of realistic sizes, we can use CP models § Based on Constitutive Equations § Allows taking into account many grains. § Large strains § Modelling of discrete grains o Anisotropy of single crystal elasticity and plasticity o Cristallographic texture § Terms of Constitutive Equations must be “calibrated” using DD § EUROfusion Engineering Grant and collaboration with UCLA (Jaime Marian and Nasr Ghoniem) § Work will start in 2020. Work Gonzalo Valles 30 / 31

Summary of computational skills of the team § At LNF we tackle the problem of radiation damage using most modelling scales. § We use well-known codes in the community and develop our own in-house codes. § Simulation techniques: o Ab initio, o Molecular Dynamics, o Binary Collision Approximation, o BCA-MD, o Object kinetic Monte Carlo, o Rate Theory, o Dislocation Dynamics, o Crystal Plasticity (soon). § Codes: o VASP, o SIESTA, o LAMMPS, o MARLOWE, MARLOWE-CIEMAT (in-house), o MARLOWE-LAMMPS (in-house), o MEGA-Ok. MC (in-house), o PROMIS, o MODELib. § Programming languages: C++, C, Python, Fortran 77 § Parallel programming: MPI, CUDA 31 / 31