Formal verification SAT applied in equivalence checking but

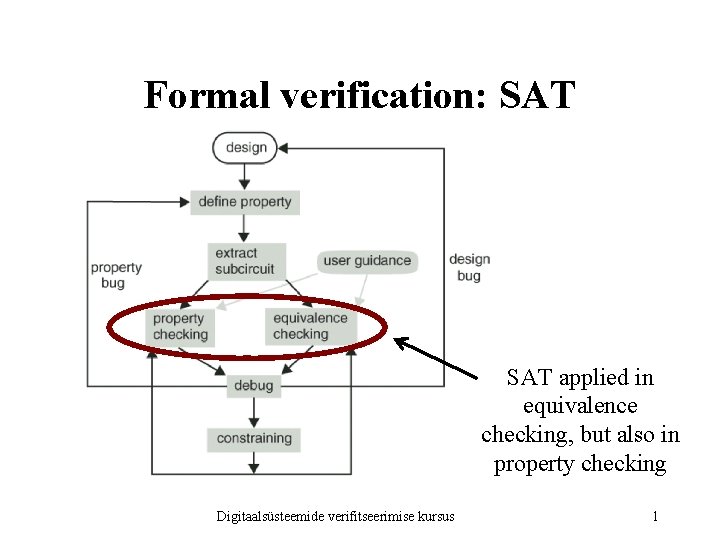
Formal verification: SAT applied in equivalence checking, but also in property checking Digitaalsüsteemide verifitseerimise kursus 1

Satisfiability aka SAT • SAT: Boolean function is satisfiable if there exists a variable assignment for which the function is TRUE Digitaalsüsteemide verifitseerimise kursus 2

Satisfiability aka SAT • SAT is transformed to CNF (i. e. product of sums). • Sums are called terms. • If terms have max 2 literals then 2 -SAT solved in a polynomial time L 3 -SAT is an NP complete task Digitaalsüsteemide verifitseerimise kursus 3

Satisfiability aka SAT • Is this CNF satisfiable? • Yes: a = 1, b = 0, c = 0! • Worst case: 2 n combinations to try Digitaalsüsteemide verifitseerimise kursus 4

Some terminology • If x in the formula alwaysin one phase (i. e. always inverted or always noninverted then x is unate. • If x in the formula in both phases then x is binate. • Term having just one literal called unit term. Digitaalsüsteemide verifitseerimise kursus 5

Resolvent-algorithm • Resolvent: f = (x+A)(¬x+B) = (x +A)(¬x+B)(A+B) • Consensus: f = x. C + ¬x. D + CD • Since SAT is in CNF we use resolvent. Digitaalsüsteemide verifitseerimise kursus 6

Resolvent-algorithm 1. 2. 3. 4. 5. 6. Choose another variable x. If x is unate, apply unate rule. If x is unit term, apply unit term rule. If x is binate, solve resolvent of x. Repeat the steps until all resolvents solved. If the result is 1, then function satisfiable; otherwise not satisfiable (unit term). Digitaalsüsteemide verifitseerimise kursus 7

Resolvent-algorithm example a binate terms resolvent Digitaalsüsteemide verifitseerimise kursus solved 8

Resolvent-algorithm: summary • Resolvent-algorithm mathematically elegant but. . . • . . . Designed for small SAT problems • In the worst case 2 n resolvents to solve • In order to solve complex SAT instances, search based algorithms needed Digitaalsüsteemide verifitseerimise kursus 9

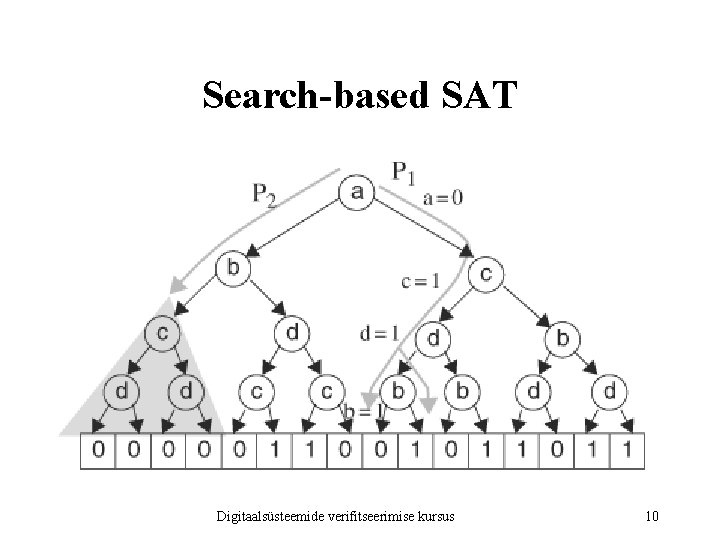
Search-based SAT Digitaalsüsteemide verifitseerimise kursus 10

Implication Graph • Directed acyclic graph: • Nodes labeled by variable names, followed by the rank of the decision • Variables preceded by minus were assigned 0, not preceded by minus were assigned 1 • Directed arcs show from which assignments what new assignments imply • Decision nodes (grey) and implication nodes (white) Digitaalsüsteemide verifitseerimise kursus 11

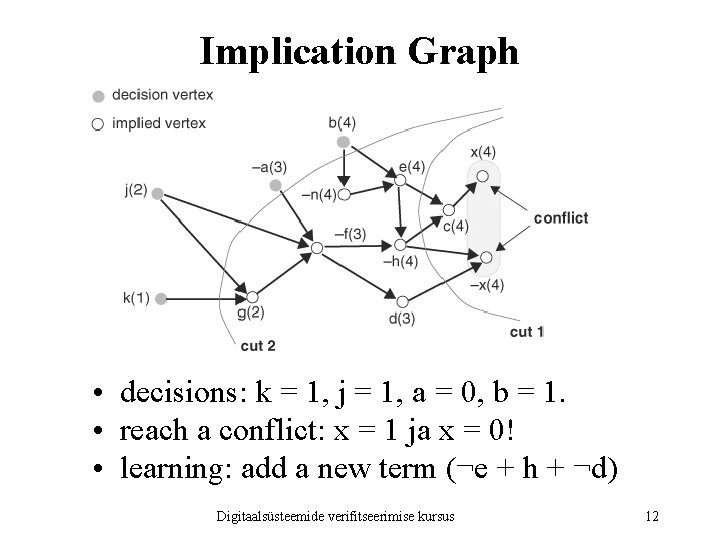
Implication Graph • decisions: k = 1, j = 1, a = 0, b = 1. • reach a conflict: x = 1 ja x = 0! • learning: add a new term (¬e + h + ¬d) Digitaalsüsteemide verifitseerimise kursus 12

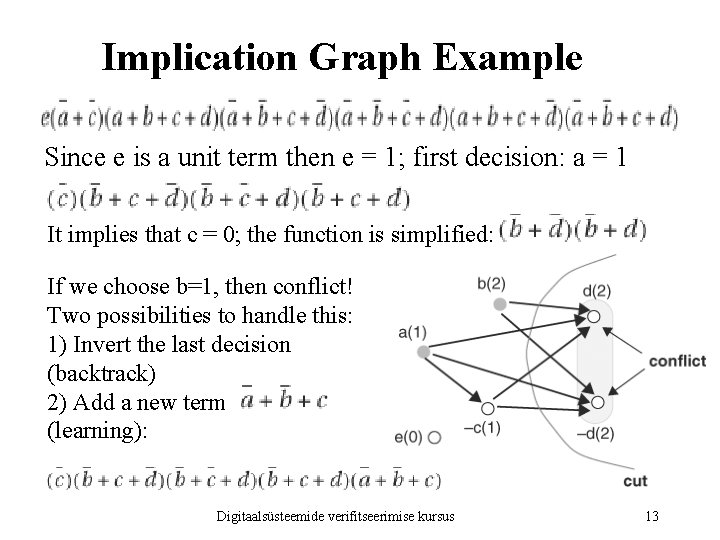
Implication Graph Example Since e is a unit term then e = 1; first decision: a = 1 It implies that c = 0; the function is simplified: If we choose b=1, then conflict! Two possibilities to handle this: 1) Invert the last decision (backtrack) 2) Add a new term (learning): Digitaalsüsteemide verifitseerimise kursus 13

Equivalence Checking • Two principal approaches: • Transform implementation and spec (reference implementation) to a canonical form • Search for an input assignment that would distinguish the responses of the implementation and reference implementation. • SAT applied for the latter Digitaalsüsteemide verifitseerimise kursus 14

Equivalence checking with SAT • Equivalence Checking can be reduced to SAT: d = f g • Iff d is satisfiable then f and g are NOT equivalent. Digitaalsüsteemide verifitseerimise kursus 15

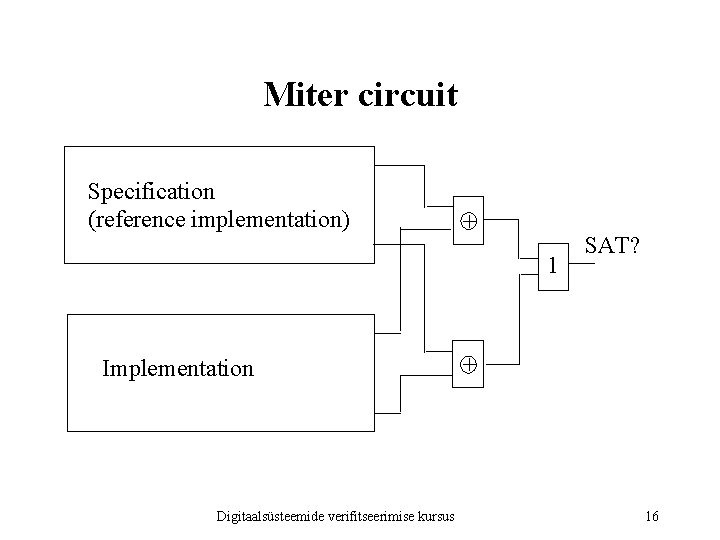
Miter circuit Specification (reference implementation) + 1 Implementation Digitaalsüsteemide verifitseerimise kursus SAT? + 16

SAT for schematics: characteristic equation • Build CNFs corresponding to logic gates using logic implication: • a b = ¬a + b a 0 0 1 1 b 0 1 Digitaalsüsteemide verifitseerimise kursus a b 1 1 0 1 17

SAT for schematics: characteristic equation • Implications for describing the AND gate: ¬a ¬c & ¬b ¬c & ¬c ¬a ¬b a b & c • Characteristic equation for AND in CNF: (a+ ¬c) (b+ ¬c) (c+ ¬a+ ¬b) Digitaalsüsteemide verifitseerimise kursus 18

SAT for schematics: characteristic equation • Implications for describing the OR-gate: a c & b c & c a b a b 1 c • Characteristic equation for OR in CNF: (¬a + c) (¬b + c) (¬c + a + b) Digitaalsüsteemide verifitseerimise kursus 19

SAT for schematics: characteristic equation a b d & c e 1 f Characteristic equation for a schematic: (a+¬d)(b+¬d)(d+¬a+¬b)(¬c+¬e)(c+e)(¬d+f)(¬e+f)(¬f+d+e) Digitaalsüsteemide verifitseerimise kursus 20