Formal Verification of UML Diagrams Jeffrey Smith Sanders

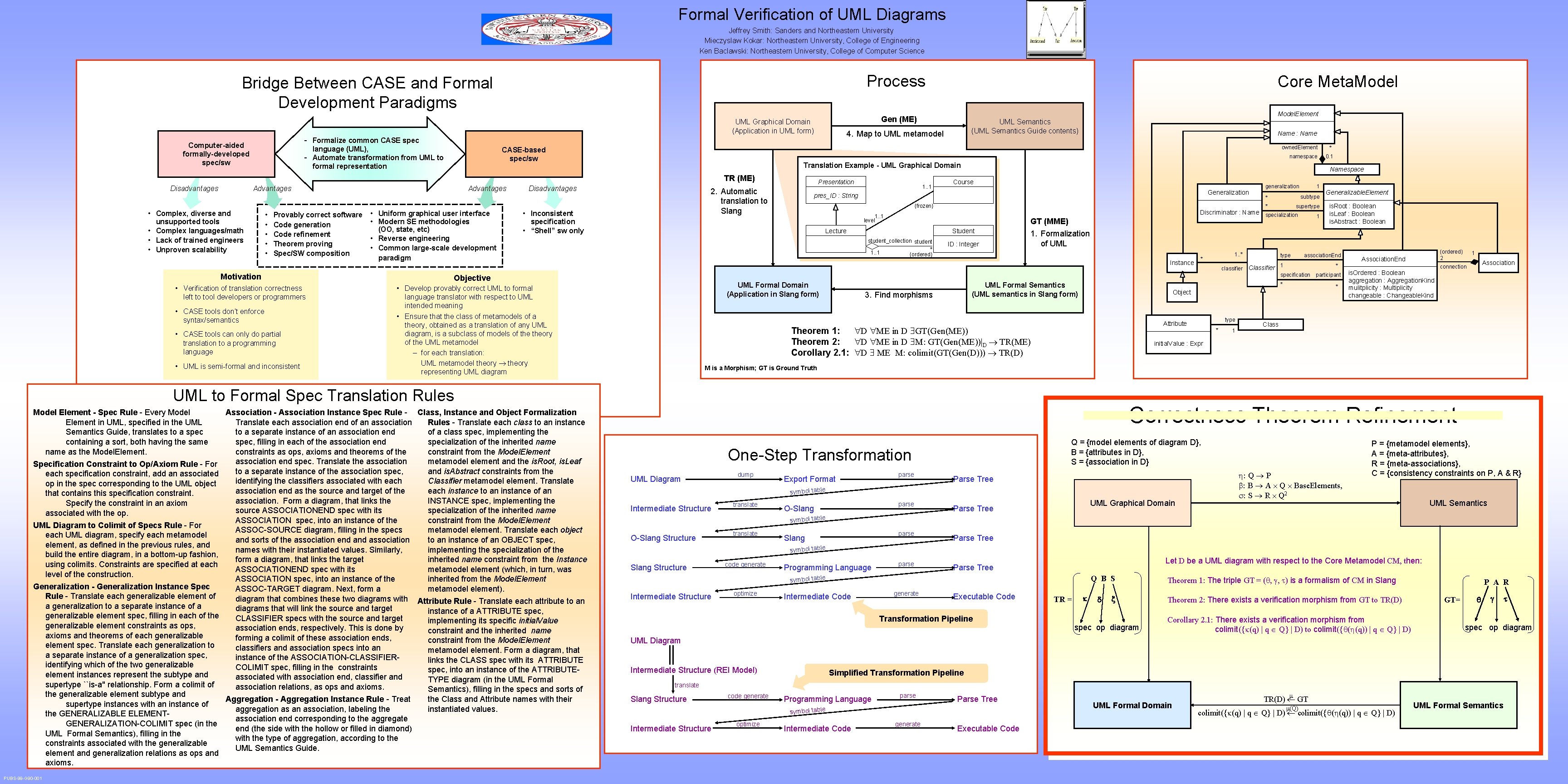
Formal Verification of UML Diagrams Jeffrey Smith: Sanders and Northeastern University Mieczyslaw Kokar: Northeastern University, College of Engineering Ken Baclawski: Northeastern University, College of Computer Science Process Bridge Between CASE and Formal Development Paradigms CASE-based spec/sw Advantages • Complex, diverse and unsupported tools • Complex languages/math • Lack of trained engineers • Unproven scalability • • • Provably correct software Code generation Code refinement Theorem proving Spec/SW composition Motivation • Verification of translation correctness left to tool developers or programmers • CASE tools don’t enforce syntax/semantics • CASE tools can only do partial translation to a programming language • UML is semi formal and inconsistent Advantages • Uniform graphical user interface • Modern SE methodologies (OO, state, etc) • Reverse engineering • Common large-scale development paradigm Name : Name Disadvantages Presentation 2. Automatic translation to Slang • Inconsistent specification • “Shell” sw only 1. . 1 Course Generalization pres_ID : String {frozen} 1. . 1 level Specification Constraint to Op/Axiom Rule For each specification constraint, add an associated op in the spec corresponding to the UML object that contains this specification constraint. Specify the constraint in an axiom associated with the op. UML Diagram to Colimit of Specs Rule For each UML diagram, specify each metamodel element, as defined in the previous rules, and build the entire diagram, in a bottom up fashion, using colimits. Constraints are specified at each level of the construction. Generalization - Generalization Instance Spec Rule Translate each generalizable element of a generalization to a separate instance of a generalizable element spec, filling in each of the generalizable element constraints as ops, axioms and theorems of each generalizable element spec. Translate each generalization to a separate instance of a generalization spec, identifying which of the two generalizable element instances represent the subtype and supertype ``is a" relationship. Form a colimit of the generalizable element subtype and supertype instances with an instance of the GENERALIZABLE ELEMENT GENERALIZATION COLIMIT spec (in the UML Formal Semantics), filling in the constraints associated with the generalizable element and generalization relations as ops and axioms. PUBS 99 G 90 001 namespace 0. 1 Student student_collection student * 1. . 1 {ordered} ID : Integer generalization 1 subtype * * supertype Discriminator : Name specialization GT (MME) Lecture 1 1. . * * classifier type UML Formal Domain (Application in Slang form) Classifier 1 * * UML Formal Semantics (UML semantics in Slang form) 3. Find morphisms is. Root : Boolean is. Leaf : Boolean is. Abstract : Boolean association. End specification • Develop provably correct UML to formal language translator with respect to UML intended meaning • Ensure that the class of metamodels of a theory, obtained as a translation of any UML diagram, is a subclass of models of theory of the UML metamodel – for each translation: UML metamodel theory representing UML diagram Generalizable. Element 1. Formalization of UML Instance Objective Association - Association Instance Spec Rule Class, Instance and Object Formalization Translate each association end of an association Rules Translate each class to an instance to a separate instance of an association end of a class spec, implementing the spec, filling in each of the association end specialization of the inherited name constraints as ops, axioms and theorems of the constraint from the Model. Element association end spec. Translate the association metamodel element and the is. Root, is. Leaf to a separate instance of the association spec, and is. Abstract constraints from the identifying the classifiers associated with each Classifier metamodel element. Translate association end as the source and target of the each instance to an instance of an association. Form a diagram, that links the INSTANCE spec, implementing the source ASSOCIATIONEND spec with its specialization of the inherited name ASSOCIATION spec, into an instance of the constraint from the Model. Element ASSOC SOURCE diagram, filling in the specs metamodel element. Translate each object and sorts of the association end association to an instance of an OBJECT spec, names with their instantiated values. Similarly, implementing the specialization of the form a diagram, that links the target inherited name constraint from the Instance ASSOCIATIONEND spec with its metamodel element (which, in turn, was ASSOCIATION spec, into an instance of the inherited from the Model. Element ASSOC TARGET diagram. Next, form a metamodel element). diagram that combines these two diagrams with Attribute Rule Translate each attribute to an diagrams that will link the source and target instance of a ATTRIBUTE spec, CLASSIFIER specs with the source and target implementing its specific initial. Value association ends, respectively. This is done by constraint and the inherited name forming a colimit of these association ends, constraint from the Model. Element classifiers and association specs into an metamodel element. Form a diagram, that instance of the ASSOCIATION CLASSIFIER links the CLASS spec with its ATTRIBUTE COLIMIT spec, filling in the constraints spec, into an instance of the ATTRIBUTE associated with association end, classifier and TYPE diagram (in the UML Formal association relations, as ops and axioms. Semantics), filling in the specs and sorts of the Class and Attribute names with their Aggregation - Aggregation Instance Rule Treat instantiated values. aggregation as an association, labeling the association end corresponding to the aggregate end (the side with the hollow or filled in diamond) with the type of aggregation, according to the UML Semantics Guide. * Namespace type Attribute Theorem 1: D ME in D GT(Gen(ME)) Theorem 2: D ME in D M: GT(Gen(ME))|D TR(ME) Corollary 2. 1: D ME M: colimit(GT(Gen(D))) TR(D) * 1 participant * Object {ordered} 2 Association. End is. Ordered : Boolean aggregation : Aggregation. Kind mulitplicity : Multiplicity changeable : Changeable. Kind 1 Association connection Class initial. Value : Expr M is a Morphism; GT is Ground Truth UML to Formal Spec Translation Rules Model Element - Spec Rule Every Model Element in UML, specified in the UML Semantics Guide, translates to a spec containing a sort, both having the same name as the Model. Element. owned. Element Translation Example - UML Graphical Domain TR (ME) Disadvantages UML Semantics (UML Semantics Guide contents) 4. Map to UML metamodel Formalize common CASE spec language (UML), Automate transformation from UML to formal representation Model. Element Gen (ME) UML Graphical Domain (Application in UML form) Computer-aided formally-developed spec/sw Core Meta. Model Correctness Theorem Refinement Q = {model elements of diagram D}, B = {attributes in D}, S = {association in D} One Step Transformation UML Diagram dump Export Format parse Parse Tree symbol table Intermediate Structure translate parse O Slang UML Graphical Domain Parse Tree : Q P : B A Q Base. Elements, : S R Q 2 P = {metamodel elements}, A = {meta attributes}, R = {meta associations}, C = {consistency constraints on P, A & R} UML Semantics symbol table O Slang Structure translate parse Slang Parse Tree symbol table Slang Structure code generate Programming Language parse Let D be a UML diagram with respect to the Core Metamodel CM, then: Parse Tree Q B S symbol table Intermediate Structure optimize Intermediate Code generate Executable Code Transformation Pipeline TR = spec op diagram Theorem 1: The triple GT = ( , , ) is a formalism of CM in Slang Theorem 2: There exists a verification morphism from GT to TR(D) Corollary 2. 1: There exists a verification morphism from colimit({ (q) | q Q} | D) to colimit({ ( (q)) | q Q} | D) P A R GT= spec op diagram UML Diagram Intermediate Structure (REI Model) Simplified Transformation Pipeline translate Slang Structure code generate Programming Language parse Parse Tree symbol table Intermediate Structure optimize Intermediate Code generate Executable Code UML Formal Domain TR(D) GT (Q) colimit({ (q) | q Q} | D) colimit({ ( (q)) | q Q} | D) UML Formal Semantics

Translation Example UML Formal Domain spec LECTURE is sort Lecture op name: Lecture -> String axiom fa(a: Lecture) name(a) = "Lecture" theorem Lecture-name is fa(a: Lecture, b: Lecture) (name(a) = "Lecture" & name(b) = "Lecture") op is. Leaf: Lecture -> Boolean axiom fa(a: Lecture) is. Leaf(a) = true theorem Lecture-is. Leaf is fa(a: Lecture, b: Lecture) (is. Leaf(a) = true & is. Leaf(b) = true) op is. Root: Lecture -> Boolean axiom fa(a: Lecture) is. Root(a) = false theorem Lecture-is. Root is fa(a: Lecture, b: Lecture) (is. Root(a) = false & is. Root(b) = false) op is. Abstract: Lecture -> Boolean axiom fa(a: Lecture) is. Abstract(a) = false theorem Lecture-is. Abstract is fa(a: Lecture, b: Lecture) (is. Abstract(a) = false & is. Abstract(b) = false) end-spec COURSE is sort Course op name: Course -> String axiom fa(a: Course) name(a) = "Course" theorem Course-name is fa(a: Course, b: Course) (name(a) = "Course" & name(b) = "Course") op is. Leaf: Course -> Boolean axiom fa(a: Course) is. Leaf(a) = true theorem Course-is. Leaf is fa(a: Course, b: Course) (is. Leaf(a) = true & is. Leaf(b) = true) op is. Root: Course -> Boolean axiom fa(a: Course) is. Root(a) = true theorem Course-is. Root is fa(a: Course, b: Course) (is. Root(a) = true & is. Root(b) = true) op is. Abstract: Course -> Boolean axiom fa(a: Course) is. Abstract(a) = false theorem Course-is. Abstract is fa(a: Course, b: Course) (is. Abstract(a) = false & is. Abstract(b) = false) end-spec PRESENTATION is sort Presentation op name: Presentation -> String axiom fa(a: Presentation) name(a) = "Presentation" theorem Presentation-name is fa(a: Presentation, b: Presentation) (name(a) = "Presentation" & name(b) = "Presentation") op is. Leaf: Presentation -> Boolean axiom fa(a: Presentation) is. Leaf(a) = false theorem Presentation-is. Leaf is fa(a: Presentation, b: Presentation) (is. Leaf(a) = false & is. Leaf(b) = false) op is. Root: Presentation -> Boolean axiom fa(a: Presentation) is. Root(a) = true theorem Presentation-is. Root is fa(a: Presentation, b: Presentation) (is. Root(a) = true & is. Root(b) = true) op is. Abstract: Presentation -> Boolean axiom fa(a: Presentation) is. Abstract(a) = true theorem Presentation-is. Abstract is fa(a: Presentation, b: Presentation) (is. Abstract(a) = true & is. Abstract(b) = true) end-spec STUDENT is sort Student op name: Student -> String axiom fa(a: Student) name(a) = "Student" theorem Student-name is fa(a: Student, b: Student) (name(a) = "Student" & name(b) = "Student") op is. Leaf: Student -> Boolean axiom fa(a: Student) is. Leaf(a) = true theorem Student-is. Leaf is fa(a: Student, b: Student) (is. Leaf(a) = true & is. Leaf(b) = true) op is. Root: Student -> Boolean axiom fa(a: Student) is. Root(a) = true theorem Student-is. Root is fa(a: Student, b: Student) (is. Root(a) = true & is. Root(b) = true) op is. Abstract: Student -> Boolean axiom fa(a: Student) is. Abstract(a) = false theorem Student-is. Abstract is fa(a: Student, b: Student) (is. Abstract(a) = false & is. Abstract(b) = false) end-spec PRES_ID-ATTRIBUTE is sort pres_ID-attribute op name: pres_ID-attribute -> String axiom fa(a: pres_ID-attribute) name(a) = "pres_ID" theorem pres_ID-name is fa(a: pres_ID-attribute, b: pres_ID-attribute) PUBS 99 G 90 001 (name(a) = "pres_ID" & name(b) = "pres_ID") op pres_ID: pres_ID-attribute -> String axiom fa(a: pres_ID-attribute) pres_ID(a) = "" theorem pres_ID-initial. Value is fa(a: pres_ID-attribute, b: pres_ID-attribute) (pres_ID(a) = "" & pres_ID(b) = "") end-spec theorem Student-AE-Lecture-is. Ordered is fa(a: Student-AE-Lecture, b: Student-AE-Lecture) (is. Ordered(a) = true & is. Ordered(b) = true) end-spec LECTURE-AE-COURSE is sort Lecture-AE-Course op name: Lecture-AE-Course -> String diagram PRES_ID-ATTRIBUTE is axiom fa(a: Lecture-AE-Course) name(a) = "level" nodes T 1: TRIV, T 2: TRIV, PAIR, PRESENTATION, theorem Lecture-AE-Course-name is PRES_ID-ATTRIBUTE fa(a: Lecture-AE-Course, b: Lecture-AE-Course) arcs (name(a) = "level" & name(b) = "level") T 1 -> PRESENTATION: {e -> Presentation}, op multiplicity: Lecture-AE-Course -> Nat, Nat T 1 -> PAIR: {e -> Left}, axiom fa(a: Lecture-AE-Course) multiplicity(a) = (1, 1) T 1 -> PAIR: {e -> Right}, theorem Lecture-AE-Course-multiplicity is T 1 -> PRES_ID-ATTRIBUTE: {e -> pres_ID-attribute} fa(a: Lecture-AE-Course, b: Lecture-AE-Course) end-diagram (multiplicity(a) = (1, 1) & multiplicity(b) = (1, 1)) op is. Navigable: Lecture-AE-Course -> Boolean spec ID-ATTRIBUTE is axiom fa(a: Lecture-AE-Course) is. Navigable(a) = true sort ID-attribute theorem Lecture-AE-Course-is. Navigable is op name: ID-attribute -> String fa(a: Lecture-AE-Course, b: Lecture-AE-Course) axiom fa(a: ID-attribute) name(a) = "ID" (is. Navigable(a) = true & is. Navigable(b) = true) theorem ID-name is op aggregate: Lecture-AE-Course -> String fa(a: ID-attribute, b: ID-attribute) axiom fa(a: Lecture-AE-Course) aggregate(a) = "none" (name(a) = "ID" & name(b) = "ID") theorem Lecture-AE-Course-aggregate is op ID: ID-attribute -> Integer fa(a: Lecture-AE-Course, b: Lecture-AE-Course) axiom fa(a: ID-attribute) ID(a) = "" (aggregate(a) = "none" & aggregate(b) = "none") theorem ID-initial. Value is op changeable: Lecture-AE-Course -> String fa(a: ID-attribute, b: ID-attribute) axiom fa(a: Lecture-AE-Course) changeable(a) = "none" (pres_ID(a) = "" & pres_ID(b) = "") theorem Lecture-AE-Course-changeable is end-spec fa(a: Lecture-AE-Course, b: Lecture-AE-Course) (changeable(a) = "none" & changeable(b) = "none") diagram ID-ATTRIBUTE is op is. Ordered: Lecture-AE-Course -> Boolean nodes T 1: TRIV, T 2: TRIV, PAIR, STUDENT, ID-ATTRIBUTE axiom fa(a: Lecture-AE-Course) is. Ordered(a) = false arcs theorem Lecture-AE-Course-is. Ordered is T 1 -> STUDENT: {e -> Student}, fa(a: Lecture-AE-Course, b: Lecture-AE-Course) T 1 -> PAIR: {e -> Left}, (is. Ordered(a) = false & is. Ordered(b) = false) T 1 -> PAIR: {e -> Right}, end-spec T 1 -> ID-ATTRIBUTE: {e -> ID-attribute} end-diagram spec COURSE-AE-LECTURE is sort Course-AE-Lecture spec LECTURE-AE-STUDENT is op name: Course-AE-Lecture -> String sort Lecture-AE-Student axiom fa(a: Course-AE-Lecture) name(a) = "" op name: Lecture-AE-Student -> String theorem Course-AE-Lecture-name is axiom fa(a: Lecture-AE-Student) name(a) = "student_collection" fa(a: Course-AE-Lecture, b: Course-AE-Lecture) theorem Lecture-AE-Student-name is (name(a) = "" & name(b) = "") fa(a: Lecture-AE-Student, b: Lecture-AE-Student) op multiplicity: Course-AE-Lecture -> Nat, Nat (name(a) = "student_collection" & name(b) = axiom fa(a: Course-AE-Lecture) multiplicity(a) = (1, 1) "student_collection") theorem Course-AE-Lecture-multiplicity is op multiplicity: Lecture-AE-Student -> Nat, Nat fa(a: Course-AE-Lecture, b: Course-AE-Lecture) axiom fa(a: Lecture-AE-Student) multiplicity(a) = (1, 1) (multiplicity(a) = (1, 1) & multiplicity(b) = (1, 1)) theorem Lecture-AE-Student-multiplicity is op is. Navigable: Course-AE-Lecture -> Boolean fa(a: Lecture-AE-Student, b: Lecture-AE-Student) axiom fa(a: Course-AE-Lecture) is. Navigable(a) = true (multiplicity(a) = (1, 1) & multiplicity(b) = (1, 1)) theorem Course-AE-Lecture-is. Navigable is op is. Navigable: Lecture-AE-Student -> Boolean fa(a: Course-AE-Lecture, b: Course-AE-Lecture) axiom fa(a: Lecture-AE-Student) is. Navigable(a) = true (is. Navigable(a) = true & is. Navigable(b) = true) theorem Lecture-AE-Student-is. Navigable is op aggregate: Course-AE-Lecture -> String fa(a: Lecture-AE-Student, b: Lecture-AE-Student) axiom fa(a: Course-AE-Lecture) aggregate(a) = "none" (is. Navigable(a) = true & is. Navigable(b) = true) theorem Course-AE-Lecture-aggregate is op aggregate: Lecture-AE-Student -> String fa(a: Course-AE-Lecture, b: Course-AE-Lecture) axiom fa(a: Lecture-AE-Student) aggregate(a) = "aggregate" (aggregate(a) = "none" & aggregate(b) = "none") theorem Lecture-AE-Student-aggregate is op changeable: Course-AE-Lecture -> String fa(a: Lecture-AE-Student, b: Lecture-AE-Student) axiom fa(a: Course-AE-Lecture)changeable(a) = "frozen" (aggregate(a) = "aggregate" & aggregate(b) = "aggregate") theorem Course-AE-Lecture-changeable is op changeable: Lecture-AE-Student -> String fa(a: Course-AE-Lecture, b: Course-AE-Lecture) axiom fa(a: Lecture-AE-Student) changeable(a) = "none" (changeable(a) = "frozen" & changeable(b) = "frozen") theorem Lecture-AE-Student-changeable is op is. Ordered: Course-AE-Lecture -> Boolean fa(a: Lecture-AE-Student, b: Lecture-AE-Student) axiom fa(a: Course-AE-Lecture) is. Ordered(a) = false (changeable(a) = "none" & changeable(b) = "none") theorem Course-AE-Lecture-is. Ordered is op is. Ordered: Lecture-AE-Student -> Boolean fa(a: Course-AE-Lecture, b: Course-AE-Lecture) axiom fa(a: Lecture-AE-Student) is. Ordered(a) = false (is. Ordered(a) = false & is. Ordered(b) = false) theorem Lecture-AE-Student-is. Ordered is end-spec fa(a: Lecture-AE-Student, b: Lecture-AE-Student) (is. Ordered(a) = false & is. Ordered(b) = false) spec LECTURE-STUDENT-AGGREGATION is end-spec sort Lecture-Student-Aggregation, Lecture, Student op name: Lecture-Student-Aggregation -> String spec STUDENT-AE-LECTURE is axiom fa(a: Lecture-Student-Aggregation) name(a) = sort Student-AE-Lecture "Lecture-Student-Aggregation" op name: Student-AE-Lecture -> String theorem Lecture-Student-Aggregation-name is axiom fa(a: Student-AE-Lecture) name(a) = "student" fa(a: Lecture-Student-Aggregation, theorem Student-AE-Lecture-name is b: Lecture-Student-Aggregation) fa(a: Student-AE-Lecture, b: Student-AE-Lecture) (name(a) = "Lecture-Student-Aggregation" & (name(a) = "student" & name(b) = "student") name(b) = "Lecture-Student-Aggregation") op multiplicity: Student-AE-Lecture -> Nat, Nat op is. Leaf: Lecture-Student-Aggregation -> Boolean axiom fa(a: Student-AE-Lecture) multiplicity(a) = (0, *) axiom fa(a: Lecture-Student-Aggregation) is. Leaf(a) = true theorem Student-AE-Lecture-multiplicity is theorem Lecture-Student-Aggregation-is. Leaf is fa(a: Student-AE-Lecture, b: Student-AE-Lecture) fa(a: Lecture-Student-Aggregation, b: Lecture-Student-Aggregation) (multiplicity(a) = (0, *) & multiplicity(b) = (0, *)) (is. Leaf(a) = true & is. Leaf(b) = true) op is. Navigable: Student-AE-Lecture -> Boolean op is. Root: Lecture-Student-Aggregation -> Boolean axiom fa(a: Student-AE-Lecture) is. Navigable(a) = true axiom fa(a: Lecture-Student-Aggregation) is. Root(a) = true theorem Student-AE-Lecture-is. Navigable is theorem Lecture-Student-Aggregation-is. Root is fa(a: Student-AE-Lecture, b: Student-AE-Lecture) fa(a: Lecture-Student-Aggregation, b: Lecture-Student-Aggregation) (is. Navigable(a) = true & is. Navigable(b) = true) (is. Root(a) = true & is. Root(b) = true) op aggregate: Student-AE-Lecture -> String op is. Abstract: Lecture-Student-Aggregation -> Boolean axiom fa(a: Student-AE-Lecture) aggregate(a) = "none" axiom fa(a: Lecture-Student-Aggregation) is. Abstract(a) = true theorem Student-AE-Lecture-aggregate is theorem Lecture-Student-Aggregation-is. Abstract is fa(a: Student-AE-Lecture, b: Student-AE-Lecture) fa(a: Lecture-Student-Aggregation, b: Lecture-Student-Aggregation) (aggregate(a) = "none" & aggregate(b) = "none") (is. Abstract(a) = true & is. Abstract(b) = true) op changeable: Student-AE-Lecture -> String op make-association: Lecture, Student -> Lecture-Student-Aggregation axiom fa(a: Student-AE-Lecture) changeable(a) = "none" op first: Lecture-Student-Aggregation -> Lecture theorem Student-AE-Lecture-changeable is op second: Lecture-Student-Aggregation -> Student fa(a: Student-AE-Lecture, b: Student-AE-Lecture) axiom first(make-association(d, e)) = d (changeable(a) = "none" & changeable(b) = "none") axiom second(make-association(d, e)) = e op is. Ordered: Student-AE-Lecture -> Boolean constructors {make-association} construct Lecture-Student-Aggregation axiom fa(a: Student-AE-Lecture) is. Ordered(a) = true theorem p = make-association(first(p), second(p)) end-spec diagram LECTURE-STUDENT-ASSOC-SOURCE is nodes T 1: TRIV, T 2: TRIV, PAIR, LECTURE-STUDENT-AGGREGATION, LECTURE-AE-STUDENT arcs T 1 -> LECTURE-STUDENT-AGGREGATION: {e -> Lecture-Student-Aggregation}, T 1 -> P 1: {e -> Right}, T 2 -> P 1: {e -> Left}, T 2 -> LECTURE-AE-STUDENT: {e -> Lecture-AE-Student} end-diagram LECTURE-STUDENT-ASSOC-TARGET is nodes T 1: TRIV, T 2: TRIV, PAIR, LECTURE-STUDENT-AGGREGATION, STUDENT-AE-LECTURE arcs T 1 -> LECTURE-STUDENT-AGGREGATION: {e -> Lecture-Student-Aggregation}, T 1 -> P 1: {e -> Right}, T 2 -> P 1: {e -> Left}, T 2 -> STUDENT-AE-LECTURE: {e -> Student-AE-Lecture} end-diagram spec LECTURE-STUDENT-AGGREGATION-COLIMIT is import colimit of diagram nodes T 1: TRIV, T 2: TRIV, T 3: TRIV, T 4: TRIV, T 5: TRIV, T 6: TRIV, T 7: TRIV, T 8: TRIV, P 1: PAIR, P 2: PAIR, P 3: PAIR, P 4: PAIR, LECTURE, STUDENT, LECTURE-AE-STUDENT, STUDENT-AE-LECTURE, LECTURE-STUDENT-AGGREGATION arcs T 1 -> P 1: {e -> Right}, T 2 -> P 1: {e -> Left}, T 1 -> LECTURE: {e -> Lecture}, T 2 -> LECTURE-AE-STUDENT: {e -> Lecture-AE-Student}, T 3 -> P 2: {e -> Right}, T 4 -> P 2: {e -> Left}, T 3 -> LECTURE-AE-STUDENT: {e -> Lecture-AE-Student}, T 4 -> LECTURE-STUDENT-AGGREGATION: {e -> Lecture-Student-Aggregation}, T 5 -> P 3: {e -> Right}, T 6 -> P 3: {e -> Left}, T 5 -> LECTURE-STUDENT-AGGREGATION: {e -> Lecture-Student-Aggregation}, T 6 -> STUDENT-AE-LECTURE: {e -> Student-AE-Lecture}, T 7 -> P 4: {e -> Right}, T 8 -> P 4: {e -> Left}, T 7 -> STUDENT-AE-LECTURE: {e -> Student-AE-Lecture}, T 8 -> STUDENT: {e -> Student} end-diagram axiom OCL 1 is fa(a: Lecture-AE-Student, b: Student-AE-Lecture) name(a) = name(b) => a = b axiom OCL 2 is fa(a: Lecture-AE-Student, b: Student-AE-Lecture) ((aggregate(a) = "aggregate") or (aggregate(a) = "composite") => (aggregate(b) = "none") or ((aggregate(b) = "aggregate") or (aggregate(b) = "composite") => (aggregate(a) = "none")) axiom OCL 3 is fa(a: Lecture-Student-Aggregation) Lecture = first(a) & Student = second(a) axiom OCL 4 is fa(a: Lecture, b: Student) name(a) = name(b) => a = b end-spec LECTURE-COURSE-ASSOCIATION is sort Lecture-Course-Association, Lecture, Course op name: Lecture-Course-Association -> String axiom fa(a: Lecture-Course-Association) name(a) = "Lecture-Course-Association" theorem Lecture-Course-Association-name is fa(a: Lecture-Course-Association, b: Lecture-Course-Association) (name(a) = "Lecture-Course-Association" & name(b) = "Lecture-Course-Association") op is. Leaf: Lecture-Course-Association -> Boolean axiom fa(a: Lecture-Course-Association) is. Leaf(a) = true theorem Lecture-Course-Association-is. Leaf is fa(a: Lecture-Course-Association, b: Lecture-Course-Association) (is. Leaf(a) = true & is. Leaf(b) = true) op is. Root: Lecture-Course-Association -> Boolean axiom fa(a: Lecture-Course-Association) is. Root(a) = true theorem Lecture-Course-Association-is. Root is fa(a: Lecture-Course-Association, b: Lecture-Course-Association) (is. Root(a) = true & is. Root(b) = true) op is. Abstract: Lecture-Course-Association -> Boolean axiom fa(a: Lecture-Course-Association) is. Abstract(a) = true theorem Lecture-Course-Association-is. Abstract is fa(a: Lecture-Course-Association, b: Lecture-Course-Association) (is. Abstract(a) = true & is. Abstract(b) = true) op make-association: Lecture, Course -> Lecture-Course-Association op first: Lecture-Course-Association -> Lecture op second: Lecture-Course-Association -> Course axiom first(make-association(d, e)) = d axiom second(make-association(d, e)) = e constructors {make-association} construct Lecture-Course-Association theorem p = make-association(first(p), second(p)) end-spec diagram LECTURE-COURSE-ASSOC-SOURCE is nodes T 1: TRIV, T 2: TRIV, PAIR, LECTURE-COURSE-ASSOCIATION, LECTURE-AE-COURSE arcs T 1 -> LECTURE-COURSE-ASSOCIATION: {e -> Lecture-Course-Association}, T 1 -> P 1: {e -> Right}, T 2 -> P 1: {e -> Left}, T 2 -> LECTURE-AE-COURSE: {e -> Lecture-AE-Course} end-diagram Translation Example UML Formal Semantics diagram LECTURE-COURSE-ASSOC-TARGET is nodes T 1: TRIV, T 2: TRIV, PAIR, LECTURE-COURSE-ASSOCIATION, COURSE-AE-LECTURE arcs T 1 -> LECTURE-COURSE-ASSOCIATION: {e -> Lecture-Course-Association}, T 1 -> P 1: {e -> Right}, T 2 -> P 1: {e -> Left}, T 2 -> COURSE-AE-LECTURE: {e -> Course-AE-Lecture} end-diagram spec LECTURE-COURSE-ASSOCIATION-COLIMIT is import colimit of diagram nodes T 1: TRIV, T 2: TRIV, T 3: TRIV, T 4: TRIV, T 5: TRIV, T 6: TRIV, T 7: TRIV, T 8: TRIV, P 1: PAIR, P 2: PAIR, P 3: PAIR, P 4: PAIR, LECTURE, COURSE, LECTURE-AE-COURSE, COURSE-AE-LECTURE, LECTURE-COURSE-ASSOCIATION arcs T 1 -> P 1: {e -> Right}, T 2 -> P 1: {e -> Left}, T 1 -> LECTURE: {e -> Lecture}, T 2 -> LECTURE-AE-COURSE: {e -> Lecture-AE-Course}, T 3 -> P 2: {e -> Right}, T 4 -> P 2: {e -> Left}, T 3 -> LECTURE-AE-COURSE: {e -> Lecture-AE-Course}, T 4 -> LECTURE-COURSE-ASSOCIATION: {e -> Lecture-Course-Association}, T 5 -> P 3: {e -> Right}, T 6 -> P 3: {e -> Left}, T 5 -> LECTURE-COURSE-ASSOCIATION: {e -> Lecture-Course-Association}, T 6 -> COURSE-AE-LECTURE: {e -> Course-AE-Lecture}, T 7 -> P 4: {e -> Right}, T 8 -> P 4: {e -> Left}, T 7 -> COURSE-AE-LECTURE: {e -> Course-AE-Lecture}, T 8 -> COURSE: {e -> Course} end-diagram axiom OCL 1 is fa(a: Lecture-AE-Course, b: Course-AE-Lecture) name(a) = name(b) => a = b axiom OCL 2 is fa(a: Lecture-AE-Course, b: Course-AE-Lecture) ((aggregate(a) = "aggregate") or (aggregate(a) = "composite") => (aggregate(b) = "none") or ((aggregate(b) = "aggregate") or (aggregate(b) = "composite") => (aggregate(a) = "none")) axiom OCL 3 is fa(a: Lecture-Course-Association) Lecture = first(a) & Course = second(a) axiom OCL 4 is fa(a: Lecture, b: Course) name(a) = name(b) => a = b end-spec PRESENTATION-LECTURE-GENERALIZATION is sorts Presentation-Lecture-Generalization, Lecture op name: Presentation-Lecture-Generalization -> String axiom fa(a: Presentation-Lecture-Generalization) name(a) = "Presentation-Lecture-Generalization" theorem Presentation-Lecture-Generalization-name is fa(a: Presentation-Lecture-Generalization, b: Presentation-Lecture-Generalization) (name(a) = "Presentation-Lecture-Generalization" & name(b) = "Presentation-Lecture-Generalization") op discriminator: Presentation-Lecture-Generalization -> String axiom fa(a: Presentation-Lecture-Generalization) discriminator(a) = "") theorem Presentation-Lecture-Generalization-discriminator is fa(a: Presentation-Lecture-Generalization, b: Presentation-Lecture-Generalization) (discriminator(a) = "" & discriminator(b) = "") op isa: Lecture -> Presentation-Lecture-Generalization axiom fa(a: Lecture) isa(a) = Presentation-Lecture-Generalization) theorem Presentation-Lecture-Generalization-isa is fa(a: Lecture, b: Lecture) (isa(a) = Presentation-Lecture-Generalization & isa(b) = Presentation-Lecture-Generalization) op no-isa: Presentation-Lecture-Generalization -> String axiom fa(a: Presentation-Lecture-Generalization) no-isa(a) = "Presentation" theorem Presentation-Lecture-Generalization-no-isa is fa(a: Presentation-Lecture-Generalization, b: Presentation-Lecture-Generalization) (no-isa(a) = "Presentation" & no-isa(b) = "Presentation") end-spec PRESENTATION-LECTURE-GENERALIZATION-COLIMIT is import colimit of diagram nodes T 1: TRIV, T 2: TRIV, T 3: TRIV, T 4: TRIV, P 1: PAIR, P 2: PAIR, PRESENTATION, LECTURE, PRESENTATION-LECTURE-GENERALIZATION arcs T 1 -> P 1: {e -> Left}, T 1 -> LECTURE: {e -> Lecture}, T 2 -> P 1: {e -> Right}, T 2 -> PRESENTATION-LECTURE-GENERALIZATION: {e -> Lecture}, T 3 -> P 2: {e -> Left}, T 3 -> PRESENTATION-LECTURE-GENERALIZATION: {e -> Presentation-Lecture-Generalization}, T 4 -> P 2: {e -> Right}, T 4 -> PRESENTATION: {e -> Presentation} end-diagram axiom OCL 5 is fa(a: Presentation, b: Presentation-Lecture-Generalization) is. Root(a) = no-isa(b) => "" axiom OCL 6 is fa(a: Presentation) is. Leaf(a) = false axiom OCL 7 is fa(a: Presentation, b: Presentation-Lecture-Generalization) name(a) = no-isa(b) end-spec % Part 1 specs - each of the meta-classes in the Core Metamodel ---spec PAIR is sorts Pair, Left, Right op make-pair: Left, Right -> Pair op left: Pair -> Left op right: Pair -> Right axiom (equal (left (make-pair d e)) d) axiom (equal (right(make-pair d e)) e) constructors {make-pair} construct Pair theorem (equal p (make-pair (left p) (right p))) axiom unique is (and (fa (a: Left) (ex (b: Right p: Pair) (and (equal (Left p) a) (equal (Right p) b)))) (implies (fa (a: Left b 1: Right b 2: Right p 1: Pair p 2: Pair) (and (equal (Left p 1) a) (equal (Left p 2) a)) (equal (Right p 1) b 1)) (equal (Right p 2) b 2))) (and (equal p 1 p 2) (equal b 1 b 2)))) (and (fa (a: Right) (ex (a: Left p: Pair) (and (equal (Left p) a) (equal (Right p) b)))) (implies (fa (a 1: Left a 2: Left p 1: Pair p 2: Pair b: Right) (and (equal (Left p 1) a 1) (equal (Left p 2) a 2)) (equal (Right p 1) b 1)) (equal (Right p 2) b 2))) (and (equal p 1 p 2) (equal a 1 a 2))))) end-spec MODELELEMENT is sort Model. Element op name : Model. Element -> String axiom name is (fa (a: Model. Element b: Model. Element) (equal (name a) (name b))) end-spec ATTRIBUTE is sorts Attribute, Expr op name : Attribute -> String axiom name is (fa (a: Attribute b: Attribute) (equal (name a) (name b))) op initial. Value : Attribute -> Expr axiom initial. Value is (fa (a: Attribute b: Attribute) (equal (initial. Value a) (initial. Value b))) end-spec INSTANCE is sort Instance op name : Instance -> String axiom name is (fa (a: Instance b: Instance) (equal (name a) (name b))) end-spec OBJECT is sort Object op name : Object -> String axiom name is (fa (a: Object b: Object) (equal (name a) (name b))) end-spec GENERALIZATION is sorts Generalization, Specialization op name : Generalization -> String axiom name is (fa (a: Generalization b: Generalization) (equal (name a) (name b))) op discriminator : Generalization -> String axiom discriminator is (fa (a: Generalization b: Generalization) (equal (discriminator a) (discriminator b))) op isa : Specialization -> Generalization axiom isa is (fa (a: Specialization b: Specialization) (equal (isa a) (isa b))) op no-isa : Generalization -> String axiom no-isa is (fa (a: Generalization b: Generalization) (equal (no-isa a) (no-isa b))) end-spec NAMESPACE is sort Namespace op name : Namespace -> String axiom name is (fa (a: Namespace b: Namespace) (equal (name a) (name b))) end-spec GENERALIZABLEELEMENT is sort Generalizable. Element op name : Generalizable. Element -> String axiom name is (fa (a: Generalizable. Element b: Generalizable. Element) (equal (name a) (name b))) op is. Root : Generalizable. Element -> Boolean axiom is. Root is (fa (a: Generalizable. Element b: Generalizable. Element) (equal (is. Root a) (is. Root b))) op is. Leaf : Generalizable. Element -> Boolean axiom is. Leaf is (fa (a: Generalizable. Element b: Generalizable. Element) (equal (is. Leaf a) (is. Leaf b))) op is. Abstract : Generalizable. Element -> Boolean axiom is. Abstract is (fa (a: Generalizable. Element b: Generalizable. Element) (equal (is. Abstract a) (is. Abstract b))) end-spec CLASSIFIER is sort Classifier op name : Classifier -> String axiom name is (fa (a: Classifier b: Classifier) (equal (name a) (name b))) op is. Root : Classifier -> Boolean axiom is. Root is (fa (a: Classifier b: Classifier) (equal (is. Root a) (is. Root b))) op is. Leaf : Classifier -> Boolean axiom is. Leaf is (fa (a: Classifier b: Classifier) (equal (is. Leaf a) (is. Leaf b))) op is. Abstract : Classifier -> Boolean axiom is. Abstract is (fa (a: Classifier b: Classifier) (equal (is. Abstract a) (is. Abstract b))) end-spec CLASS is sort Class op name : Class -> String axiom name is (fa (a: Class b: Class) (equal (name a) (name b))) op is. Root : Class -> Boolean axiom is. Root is (fa (a: Class b: Class) (equal (is. Root a) (is. Root b))) op is. Leaf : Class -> Boolean axiom is. Leaf is (fa (a: Class b: Class) (equal (is. Leaf a) (is. Leaf b))) op is. Abstract : Class -> Boolean axiom is. Abstract is (fa (a: Class b: Class) (equal (is. Abstract a) (is. Abstract b))) end-spec ASSOCIATION is sort Association, Source, Target op name : Association -> String axiom name is (fa (a: Association b: Association) (equal (name a) (name b))) op is. Root : Association -> Boolean axiom is. Root is (fa (a: Association b: Association) (equal (is. Root a) (is. Root b))) op is. Leaf : Association -> Boolean axiom is. Leaf is (fa (a: Association b: Association) (equal (is. Leaf a) (is. Leaf b))) op is. Abstract : Association -> Boolean axiom is. Abstract is (fa (a: Association b: Association) (equal (is. Abstract a) (is. Abstract b))) op make-association: Source, Target -> Association op first: Association -> Source op second: Association -> Target axiom (equal (first (make-association d e)) d) axiom (equal (second(make-association d e)) e) constructors {make-association} construct Association theorem (equal p (make-association (first p) (second p))) end-spec ASSOCIATIONEND is sorts Association. End op is. Navigable: Association. End -> Boolean axiom is. Navigable is (fa (a: Association. End b: Association. End) (equal (is. Navigable a) (is. Navigable b))) op is. Ordered: Association. End -> Boolean axiom is. Ordered is (fa (a: Association. End b: Association. End) (equal (is. Ordered a) (is. Ordered b))) op name: Association. End -> String axiom name is (fa (a: Association. End b: Association. End) (equal (name a) (name b))) op aggregate: Association. End -> String axiom aggregate is (fa (a: Association. End b: Association. End) (equal (aggregate a) (aggregate b))) op multiplicity: Association. End -> Nat, Nat axiom multiplicity is (fa (a: Association. End b: Association. End) (equal (multiplicity a) (multiplicity b))) op changeable: Association. End -> String axiom changeable is (fa (a: Association. End b: Association. End) (equal (changeable a) (changeable b))) end-spec % Part 2 diagrams - diagrams that implement each link between pairs of meta-classes diagram ASSOCIATION-END-TYPE is nodes T 1: TRIV, T 2: TRIV, PAIR, ASSOCIATIONEND, CLASSIFIER arcs T 1 -> ASSOCIATIONEND: {e -> Association. End}, T 1 -> PAIR: {e -> Left}, T 2 -> PAIR: {e -> Right}, T 2 -> CLASSIFIER {e -> Classifier} end-diagram SPEC-PARTICIPANT is nodes T 1: TRIV, T 2: TRIV, PAIR, ASSOCIATIONEND, CLASSIFIER arcs T 1 -> ASSOCIATIONEND: {e -> Association. End}, T 1 -> PAIR: {e -> Left}, T 2 -> PAIR: {e -> Right}, T 2 -> CLASSIFIER: {e -> Classifier} end-diagram GEN-SUBTYPE is nodes T 1: TRIV, T 2: TRIV, PAIR, GENERALIZABLEELEMENT, GENERALIZATION arcs T 1 -> GENERALIZABLEELEMENT: {e -> Generalizable. Element}, T 1 -> PAIR: {e -> Left}, T 2 -> PAIR: {e -> Right}, T 2 -> GENERALIZATION: {e -> Specialization} end-diagram GEN-SUPERTYPE is nodes T 1: TRIV, T 2: TRIV, PAIR, GENERALIZABLEELEMENT, GENERALIZATION arcs T 1 -> GENERALIZABLEELEMENT: {e -> Generalizable. Element}, T 1 -> PAIR: {e -> Left}, T 2 -> PAIR: {e -> Right}, T 2 -> GENERALIZATION: {e -> Generalization} end-diagram OWNED-EL-NAMESPACE is nodes T 1: TRIV, T 2: TRIV, PAIR, MODELELEMENT, NAMESPACE arcs T 1 -> MODELELEMENT: {e -> Model. Element}, T 1 -> PAIR: {e -> Left}, T 2 -> PAIR: {e -> Right}, T 2 -> NAMESPACE: {e -> Namespace} end-diagram ASSOC-SOURCE is nodes T 1: TRIV, T 2: TRIV, PAIR, ASSOCIATIONEND arcs T 1 -> ASSOCIATION: {e -> Source}, T 1 -> PAIR: {e -> Left}, T 2 -> PAIR: {e -> Right}, T 2 -> ASSOCIATIONEND: {e -> Association. End} end-diagram ASSOC-TARGET is nodes T 1: TRIV, T 2: TRIV, PAIR, ASSOCIATIONEND arcs T 1 -> ASSOCIATION: {e -> Target}, T 1 -> PAIR: {e -> Left}, T 2 -> PAIR: {e -> Right}, T 2 -> ASSOCIATIONEND: {e -> Association. End} end-diagram INSTANCE-CLASSIFIER is nodes T 1: TRIV, T 2: TRIV, PAIR, INSTANCE, CLASSIFIER arcs T 1 -> INSTANCE: {e -> Instance}, T 1 -> PAIR: {e -> Left}, T 2 -> PAIR: {e -> Right}, T 2 -> CLASSIFIER: {e -> Classifier} end-diagram ATTRIBUTE-TYPE is nodes T 1: TRIV, T 2: TRIV, PAIR, CLASS, ATTRIBUTE arcs T 1 -> CLASS: {e -> Class}, T 1 -> PAIR: {e -> Left}, T 2 -> PAIR: {e -> Right}, T 2 -> ATTRIBUTE: {e -> Attribute} end-diagram % Part 3 constraints - colimit specs necessary to describe the OCL constraints spec ASSOCIATION-CLASSIFIER-COLIMIT is import colimit of diagram nodes T 1: TRIV, T 2: TRIV, T 3: TRIV, T 4: TRIV, T 5: TRIV, T 6: TRIV, T 7: TRIV, T 8: TRIV, P 1: PAIR, P 2: PAIR, P 3: PAIR, P 4: PAIR, C 1: CLASSIFIER, C 2: CLASSIFIER, AE 1: ASSOCIATIONEND, AE 2: ASSOCIATIONEND, ASSOCIATION arcs T 1 -> P 1: {e -> Right}, T 2 -> P 1: {e -> Left}, T 1 -> C 1: {e -> Classifier}, T 2 -> AE 1: {e -> Association. End}, T 3 -> P 2: {e -> Right}, T 4 -> P 2: {e -> Left}, T 3 -> AE 1: {e -> Association. End}, T 4 -> ASSOCIATION: {e -> Association}, T 5 -> P 3: {e -> Right}, T 6 -> P 3: {e -> Left}, T 5 -> ASSOCIATION: {e -> Association}, T 6 -> AE 2: {e -> Association. End}, T 7 -> P 4: {e -> Right}, T 8 -> P 4: {e -> Left}, T 7 -> AE 2: {e -> Association. End}, T 8 -> C 2: {e -> Classifier} end-diagram % The Association. Ends must have a unique name within the association axiom OCL 1 is (fa(a: AE 1. Association. End b: AE 2. Association. End) (implies (equal (AE 1. name a) (AE 2. name b)) (equal AE 1. a AE 2. b))) % At most one Association. End may be an aggregate or a composite axiom OCL 2 is (fa(a: AE 1. Association. End b: AE 2. Association. End) (or (implies (or (equal (AE 1. aggregate AE 1. a) "aggregate") (equal (AE 1. aggregate AE 1. a) "composite")) (equal (AE 2. aggregate AE 2. b) "none")) (implies (or (equal (AE 2. aggregate AE 2. b) "aggregate") (equal (AE 2. aggregate AE 2. b) "composite")) (equal (AE 1. aggregate AE 1. a) "none")))) % The connected Classifiers of the Association. Ends should be included % in the Namespace of the association axiom OCL 3 is (fa(a: Association) (and (equal C 1. Classifier (first a)) (equal C 2. Classifier (second a)))) % No opposite Association. Ends may have the same name within the Classifier axiom OCL 4 is (fa(a: C 1. Classifier b: C 2. Classifier) (implies (equal (C 1. name a) (C 2. name b)) (equal C 1. a C 2. b))) end-spec GENERALIZABLEELEMENT-GENERALIZATION-COLIMIT is import colimit of diagram nodes T 1: TRIV, T 2: TRIV, T 3: TRIV, T 4: TRIV, P 1: PAIR, P 2: PAIR, GESUB: GENERALIZABLEELEMENT, GESUPER: GENERALIZABLEELEMENT, GENERALIZATION arcs T 1 -> P 1: {e -> Right}, T 1 -> GESUB: {e -> Generalizable. Element}, T 2 -> P 1: {e -> Left}, T 2 -> GENERALIZATION: {e -> Specialization}, T 3 -> P 2: {e -> Right}, T 3 -> GENERALIZATION: {e -> Generalization}, T 4 -> P 2: {e -> Left}, T 4 -> GESUPER: {e -> Generalizable. Element} end-diagram % A root cannot have any Generalizations axiom OCL 5 is (fa(a: GESUPER. Generalizable. Element b: Generalization) (implies (GESUPER. is. Root a) (equal (no-isa b. Generalization) ""))) % No Generalizable. Element can have a supertype Generalization to an % element which is a leaf axiom OCL 6 is (fa(a: Generalizable. Element) (equal (GESUPER. is. Leaf GESUPER. a) false)) % The supertype must be included in the Namespace of the Generalization axiom OCL 7 is (fa(a: GESUPER. Generalizable. Element b: Generalization) (equal (GESUPER. name GESUPER. a) b. Generalization)) end-spec

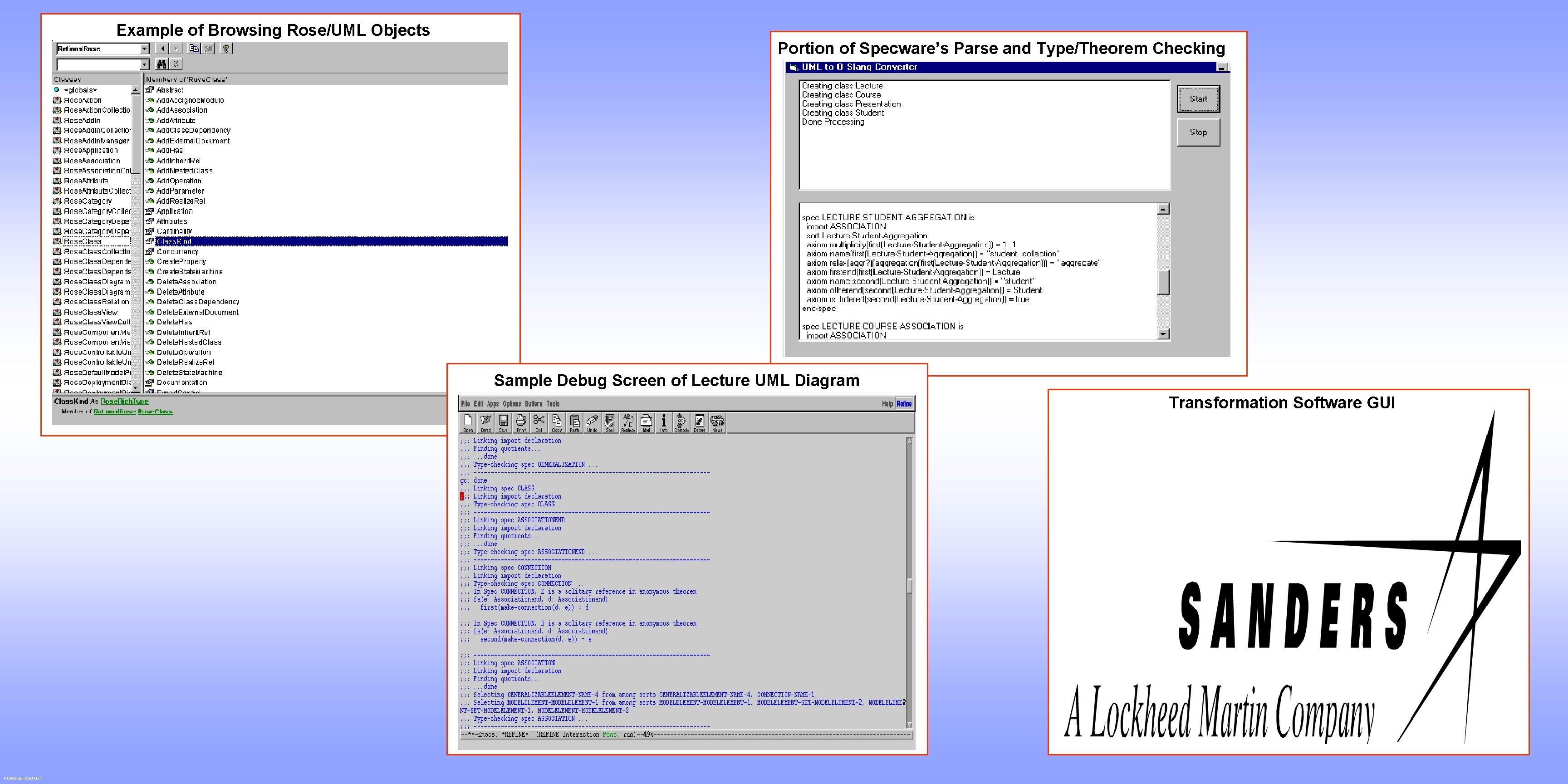
Example of Browsing Rose/UML Objects Portion of Specware’s Parse and Type/Theorem Checking Sample Debug Screen of Lecture UML Diagram Transformation Software GUI PUBS 99 G 90 001

Future Work Specware Graphical View of the Object Instance Generalization Specification UML Sample Execution • Expand on the set of meta tools future expansions include: – Translation of OCL constraints into a form consistent with math foundation – A metamodel analyzer that identifies metamodel elements, meta attributes, meta generalizations and meta associations and helps with the identification of morphisms between these meta elements and specific UML Formal Domain output – More of UML than existing core metamodel – Translation from a wider set of CASE tools – Extension of the UML Formal Domain to the level of Specware programming language primitives, supporting the potential of direct UML translation to any source code provided by Specware – Use of a wider set of theorem provers than currently built into Specware – Expansion of a CASE tool’s forward and reverse engineering functionality by including the UML Formal Domain as an intermediate representation to support richer and more complete code generation • Include reflective OCL constraints by either basing formalization on naïve set theory or building reflectivity into Specware • Contribute to future revisions of UML by streamlining redundant functionality and helping to improve the form and content of new revisions • Creation of semantics for commonly used rule based systems and translation of the UML form of these rules (and associated actions) to verifiably compose large business and military AI Systems • Develop the relationship between other theory based models, e. g. the one developed by Hartrum and Deloach, and the UML Formal Semantics constructed in this research Summary Formal Methods Systems Formalize UML - UML contributions Viable UML to Formal Methods translation Automation of human intensive processes Formal Verification of UML Diagrams Jeffrey Smith: Sanders and Northeastern University Mieczyslaw Kokar: Northeastern University, College of Engineering Ken Baclawski: Northeastern University, College of Computer Science PUBS 99 G 90 001 CASE Tools