Formal methods Tools Real Time Model Checking and





![UCb Train Crossing Communication via channels and shared variable. Stopable Area [10, 20] [3, UCb Train Crossing Communication via channels and shared variable. Stopable Area [10, 20] [3,](https://slidetodoc.com/presentation_image_h2/2d5d455cfe7d922935c2a612b65f1a0a/image-14.jpg)





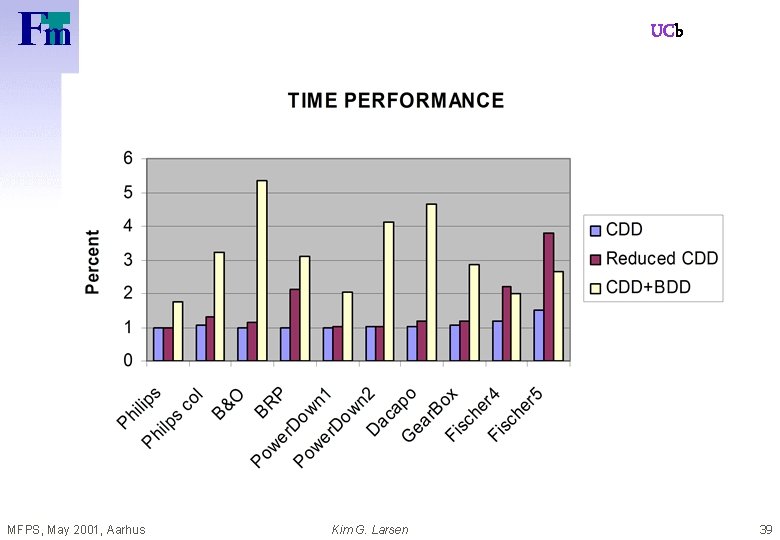
![UCb Case-Studies: Controllers z. Gearbox Controller [TACAS’ 98] z. Bang & Olufsen Power Controller UCb Case-Studies: Controllers z. Gearbox Controller [TACAS’ 98] z. Bang & Olufsen Power Controller](https://slidetodoc.com/presentation_image_h2/2d5d455cfe7d922935c2a612b65f1a0a/image-22.jpg)





















- Slides: 88

Formal methods & Tools Real Time Model Checking …and Beyond using UPPAAL 2 k Kim Guldstrand Larsen BRICS@Aalborg & FMT@Twente UCb

Tanenbaum UCb Model Checking Tools Milner, Hoare Hajek (Eindhoven) 80 PAN (Holzmann) TAU 90 SPIN (Holzman) BDDs (Bryant) CWB, AUTO, LOTOS Symbolic Model Checking (Clarke, Coudert) CESAR FDR SMV (Mc. Millan) SPIN Workshop SPIN w POR 00 MFPS, May 2001, Aarhus Kim G. Larsen 2

Tanenbaum UCb Model Checking Tools Milner, Hoare Hajek (Eindhoven) 80 w Time PAN (Holzmann) TAU 90 SPIN (Holzman) BDDs (Bryant) CWB, AUTO, LOTOS Symbolic Model Checking (Clarke, Coudert, …) CESAR FDR SMV (Mc. Millan) SPIN Workshop SPIN w POR Timed Automata (Alur, Dill) EPSILON, TAB KRONOS, Hy. Tech, UPPAAL DT SPIN, PMC 00 MFPS, May 2001, Aarhus UPPAAL 2 k Kim G. Larsen 3

Collaborators @UPPsala UCb @AALborg y Kim G Larsen y Arne Skou y Paul Pettersson y Carsten Weise y Kåre J Kristoffersen y Gerd Behrman y Thomas Hune y Oliver Möller y Wang Yi y Johan Bengtsson y Paul Pettersson y Fredrik Larsson y Alexandre David y Tobias Amnell y Oliver Möller @Elsewhere y David Griffioen, Ansgar Fehnker, Frits Vandraager, Klaus Havelund, Theo Ruys, Pedro D’Argenio, J-P Katoen, J. Tretmans, Judi Romijn, Ed Brinksma, Franck Cassez, Magnus Lindahl, Francois Laroussinie, Patricia Bouyer, Augusto Burgueno, H. Bowmann, D. Latella, M. Massink, G. Faconti, Kristina Lundqvist, Lars Asplund, Justin Pearson. . . MFPS, May 2001, Aarhus Kim G. Larsen 4

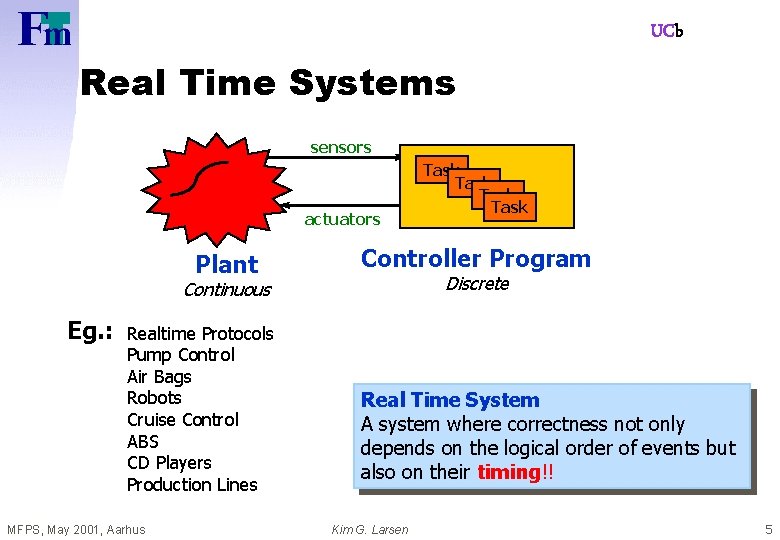
UCb Real Time Systems sensors actuators Plant Controller Program Discrete Continuous Eg. : Realtime Protocols Pump Control Air Bags Robots Cruise Control ABS CD Players Production Lines MFPS, May 2001, Aarhus Task Real Time System A system where correctness not only depends on the logical order of events but also on their timing!! Kim G. Larsen 5

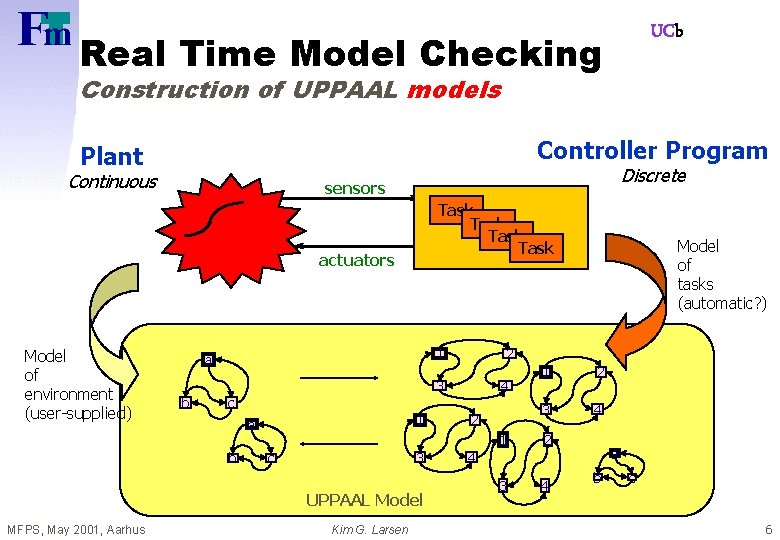
UCb Real Time Model Checking Construction of UPPAAL models Controller Program Plant Continuous Discrete sensors Task actuators Model of environment (user-supplied) 1 a 4 c 1 a b 3 c UPPAAL Model MFPS, May 2001, Aarhus 2 3 b Kim G. Larsen Model of tasks (automatic? ) 2 1 2 3 4 a 4 b c 6

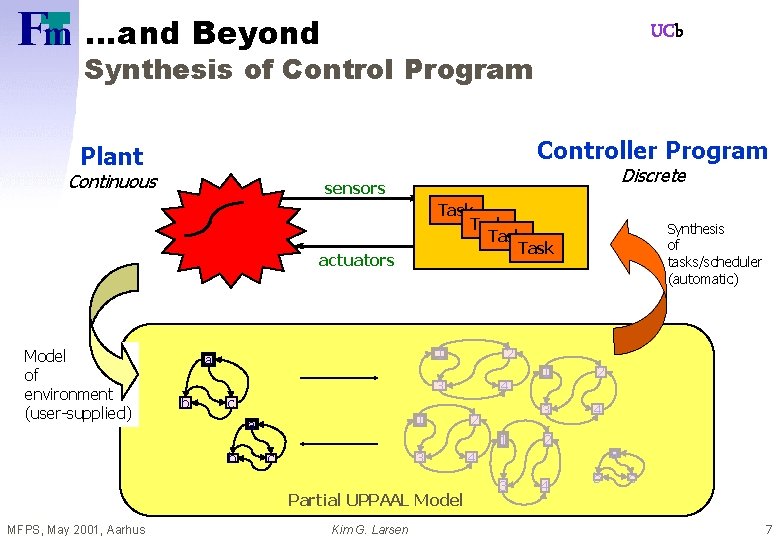
…and Beyond UCb Synthesis of Control Program Controller Program Plant Continuous Discrete sensors Task actuators Model of environment (user-supplied) 1 a 4 c 1 a b 3 c Partial UPPAAL Model MFPS, May 2001, Aarhus 2 3 b Kim G. Larsen Synthesis of tasks/scheduler (automatic) 2 1 2 3 4 a 4 b c 7

UCb Overview z UPPAAL y. Timed Automata y. Tool and Demo y. Case Studies y. Verification Engine z CUPPAAL y. Linearly Priced Timed Automata y(Optimal) Scheduling and Control Synthesis z Concluding Remarks MFPS, May 2001, Aarhus Kim G. Larsen 8

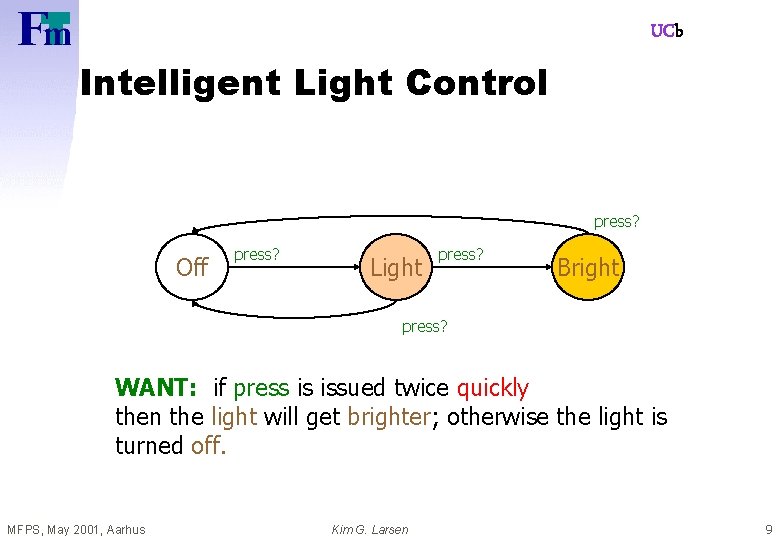
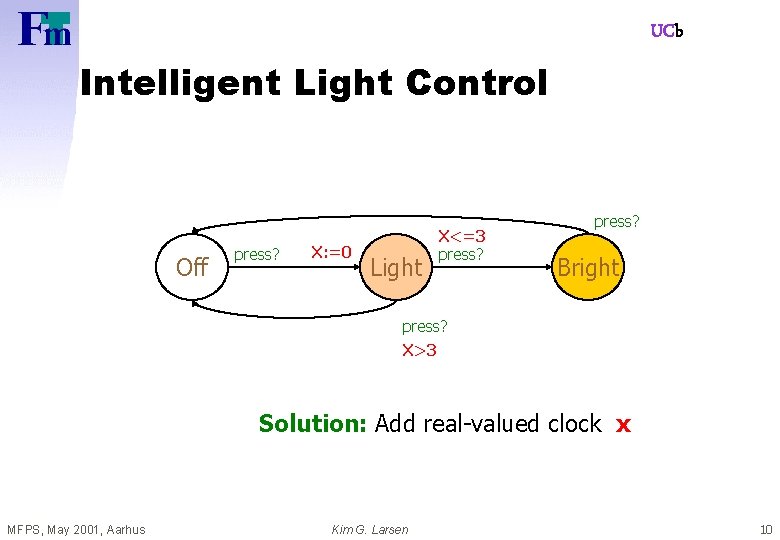
UCb Intelligent Light Control press? Off press? Light press? Bright press? WANT: if press is issued twice quickly then the light will get brighter; otherwise the light is turned off. MFPS, May 2001, Aarhus Kim G. Larsen 9

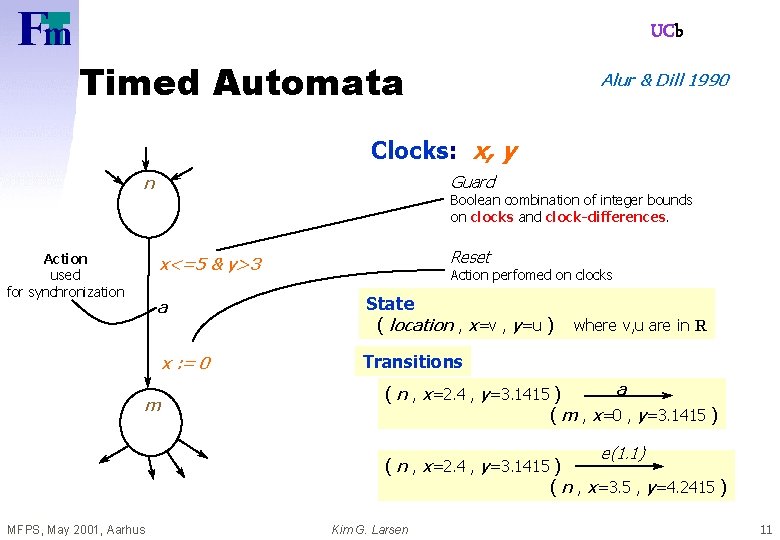
UCb Intelligent Light Control Off press? X: =0 Light X<=3 press? Bright press? X>3 Solution: Add real-valued clock x MFPS, May 2001, Aarhus Kim G. Larsen 10

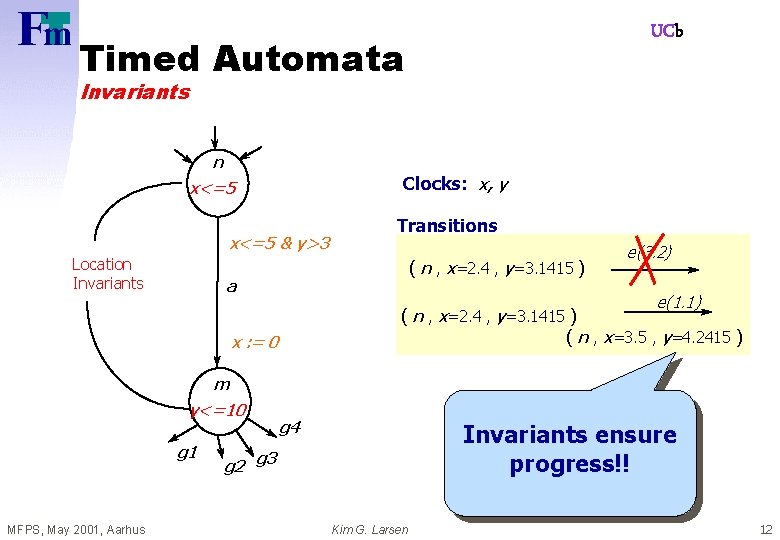
UCb Timed Automata Alur & Dill 1990 Clocks: x, y Guard n Action used for synchronization Boolean combination of integer bounds on clocks and clock-differences. Reset x<=5 & y>3 Action perfomed on clocks a State ( location , x=v , y=u ) x : = 0 Transitions m where v, u are in R a ( n , x=2. 4 , y=3. 1415 ) ( m , x=0 , y=3. 1415 ) e(1. 1) ( n , x=2. 4 , y=3. 1415 ) ( n , x=3. 5 , y=4. 2415 ) MFPS, May 2001, Aarhus Kim G. Larsen 11

UCb Timed Automata Invariants n Clocks: x, y x<=5 & y>3 Location Invariants Transitions ( n , x=2. 4 , y=3. 1415 ) a e(3. 2) e(1. 1) ( n , x=2. 4 , y=3. 1415 ) ( n , x=3. 5 , y=4. 2415 ) x : = 0 m y<=10 g 1 MFPS, May 2001, Aarhus g 4 Invariants ensure progress!! g 2 g 3 Kim G. Larsen 12

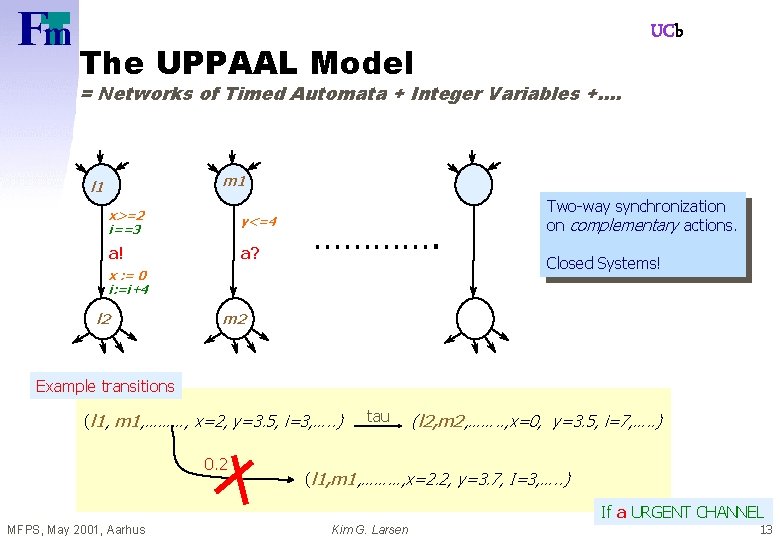
UCb The UPPAAL Model = Networks of Timed Automata + Integer Variables +…. m 1 l 1 x>=2 i==3 y<=4 a! a? …………. x : = 0 i: =i+4 l 2 Two-way synchronization on complementary actions. Closed Systems! m 2 Example transitions (l 1, m 1, ………, x=2, y=3. 5, i=3, …. . ) 0. 2 tau (l 2, m 2, ……. . , x=0, y=3. 5, i=7, …. . ) (l 1, m 1, ………, x=2. 2, y=3. 7, I=3, …. . ) If a URGENT CHANNEL MFPS, May 2001, Aarhus Kim G. Larsen 13
![UCb Train Crossing Communication via channels and shared variable Stopable Area 10 20 3 UCb Train Crossing Communication via channels and shared variable. Stopable Area [10, 20] [3,](https://slidetodoc.com/presentation_image_h2/2d5d455cfe7d922935c2a612b65f1a0a/image-14.jpg)
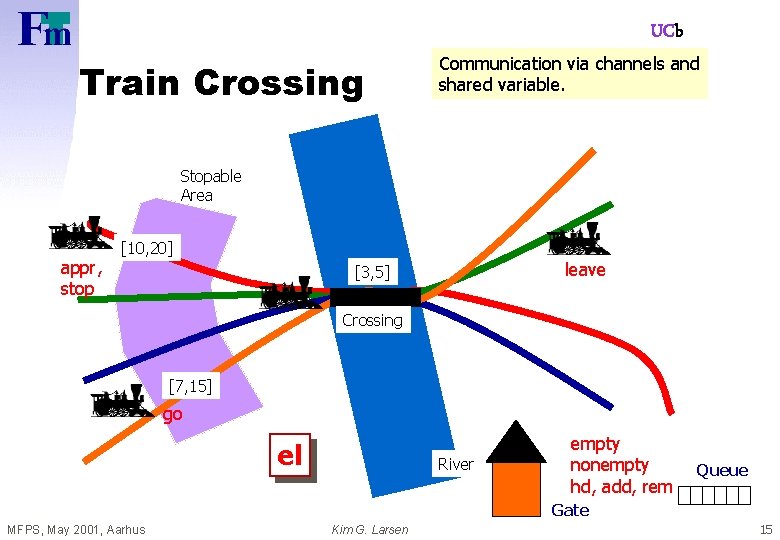
UCb Train Crossing Communication via channels and shared variable. Stopable Area [10, 20] [3, 5] Crossing [7, 15] River Queue Gate MFPS, May 2001, Aarhus Kim G. Larsen 14

UCb Train Crossing Communication via channels and shared variable. Stopable Area appr, stop [10, 20] leave [3, 5] Crossing [7, 15] go el River empty nonempty hd, add, rem Queue Gate MFPS, May 2001, Aarhus Kim G. Larsen 15

UCb LEGO Mindstorms/RCX z. Sensors: temperature, 3 output ports light, rotation, pressure. z. Actuators: motors, lamps, z. Virtual machine: y 10 tasks, 4 timers, 16 integers. 1 infra-red port 3 input ports z. Several Programming Languages: y. Not. Quite. C, Mindstorm, Robotics, leg. OS, etc. MFPS, May 2001, Aarhus Kim G. Larsen 16

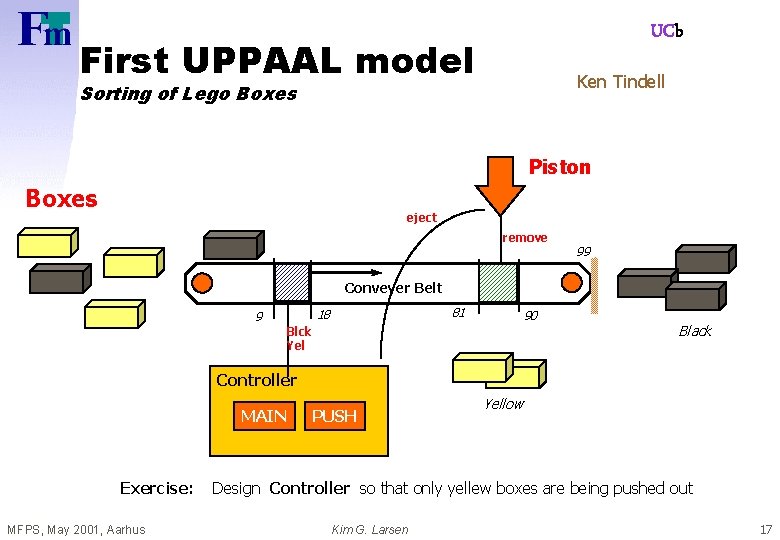
UCb First UPPAAL model Ken Tindell Sorting of Lego Boxes Piston Boxes eject remove 99 Conveyer Belt 81 18 9 90 Blck Yel Black Controller MAIN Exercise: MFPS, May 2001, Aarhus PUSH Yellow Design Controller so that only yellew boxes are being pushed out Kim G. Larsen 17

UCb int active; int DELAY; int LIGHT_LEVEL; NQC programs task MAIN{ DELAY=75; LIGHT_LEVEL=35; active=0; Sensor(IN_1, IN_LIGHT); Fwd(OUT_A, 1); Display(1); start PUSH; while(true){ wait(IN_1>=LIGHT_LEVEL); Clear. Timer(1); active=1; Play. Sound(1); wait(IN_1<LIGHT_LEVEL); } task PUSH{ while(true){ wait(Timer(1)>DELAY && active==1); active=0; Rev(OUT_C, 1); Sleep(8); Fwd(OUT_C, 1); Sleep(12); Off(OUT_C); } } } MFPS, May 2001, Aarhus Kim G. Larsen 18

Formal methods & Tools UPPAAL Demo UCb

The Production Cell in LEGO UCb Course at DTU, Copenhagen Rasmus Crüger Lund Simon Tune Riemanni Production Cell MFPS, May 2001, Aarhus Kim G. Larsen 20

UCb Case Studies: Protocols z Philips Audio Protocol [HS’ 95, CAV’ 95, RTSS’ 95, CAV’ 96] z Collision-Avoidance Protocol [SPIN’ 95] z Bounded Retransmission Protocol [TACAS’ 97] z Bang & Olufsen Audio/Video Protocol [RTSS’ 97] z TDMA Protocol [PRFTS’ 97] z Lip-Synchronization Protocol [FMICS’ 97] z Multimedia Streams [DSVIS’ 98] z ATM ABR Protocol [CAV’ 99] z ABB Fieldbus Protocol [ECRTS’ 2 k] z IEEE 1394 Firewire Root Contention (2000) MFPS, May 2001, Aarhus Kim G. Larsen 21
![UCb CaseStudies Controllers z Gearbox Controller TACAS 98 z Bang Olufsen Power Controller UCb Case-Studies: Controllers z. Gearbox Controller [TACAS’ 98] z. Bang & Olufsen Power Controller](https://slidetodoc.com/presentation_image_h2/2d5d455cfe7d922935c2a612b65f1a0a/image-22.jpg)
UCb Case-Studies: Controllers z. Gearbox Controller [TACAS’ 98] z. Bang & Olufsen Power Controller [RTPS’ 99, FTRTFT’ 2 k] z. SIDMAR Steel Production Plant [RTCSA’ 99, DSVV’ 2 k] z. Real-Time RCX Control-Programs [ECRTS’ 2 k] z. Experimental Batch Plant (2000) z. RCX Production Cell (2000) MFPS, May 2001, Aarhus Kim G. Larsen 22

Formal methods & Tools THE UPPAAL ENGINE Symbolic Reachability Checking UCb

UCb Zones From infinite to finite Symbolic state (set) (n, ) State (n, x=3. 2, y=2. 5 ) y y x MFPS, May 2001, Aarhus Zone: conjunction of x-y<=n, x<=>n x Kim G. Larsen 24

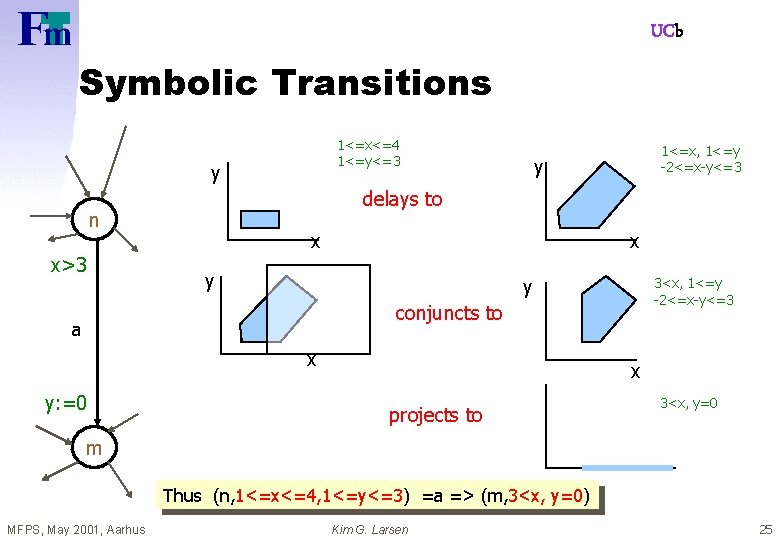
UCb Symbolic Transitions 1<=x<=4 1<=y<=3 y y delays to n x>3 1<=x, 1<=y -2<=x-y<=3 x x y y 3<x, 1<=y -2<=x-y<=3 conjuncts to a x y: =0 x projects to 3<x, y=0 m Thus (n, 1<=x<=4, 1<=y<=3) =a => (m, 3<x, y=0) MFPS, May 2001, Aarhus Kim G. Larsen 25

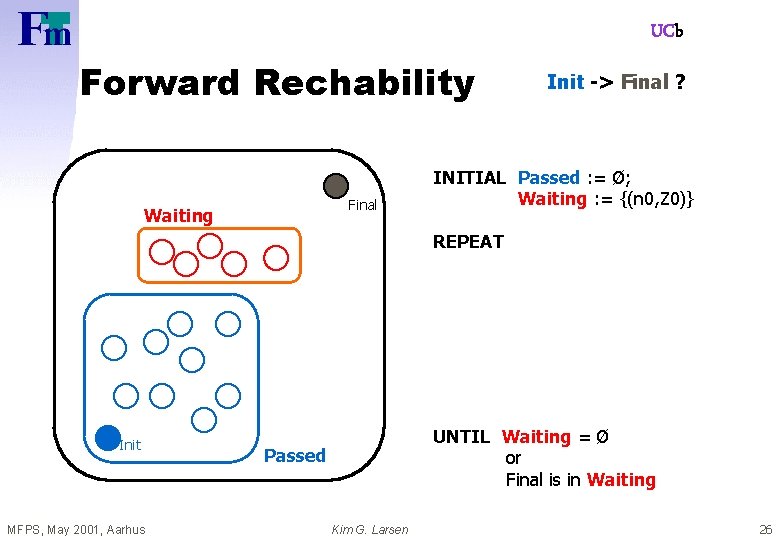
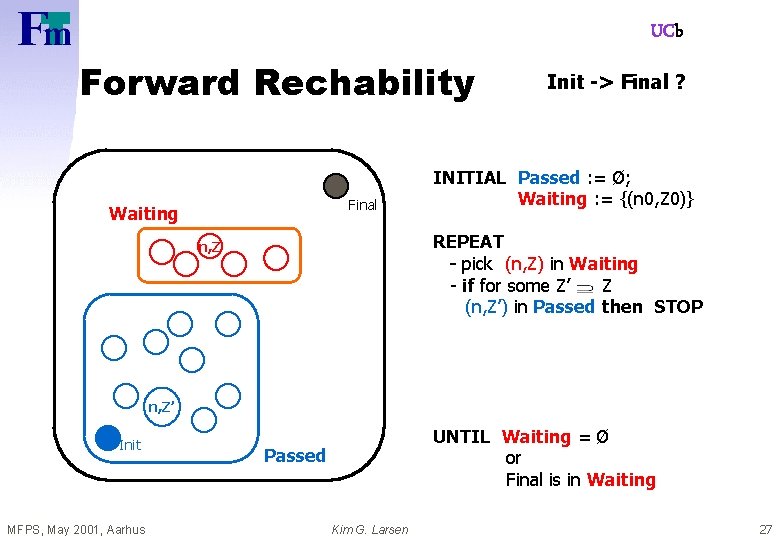
UCb Forward Rechability Final Waiting Init -> Final ? INITIAL Passed : = Ø; Waiting : = {(n 0, Z 0)} REPEAT - pick (n, Z) in Waiting - if for some Z’ Z (n, Z’) in Passed then STOP - else (explore) add { (m, U) : (n, Z) => (m, U) } to Waiting; Add (n, Z) to Passed Init MFPS, May 2001, Aarhus UNTIL Waiting = Ø or Final is in Waiting Passed Kim G. Larsen 26

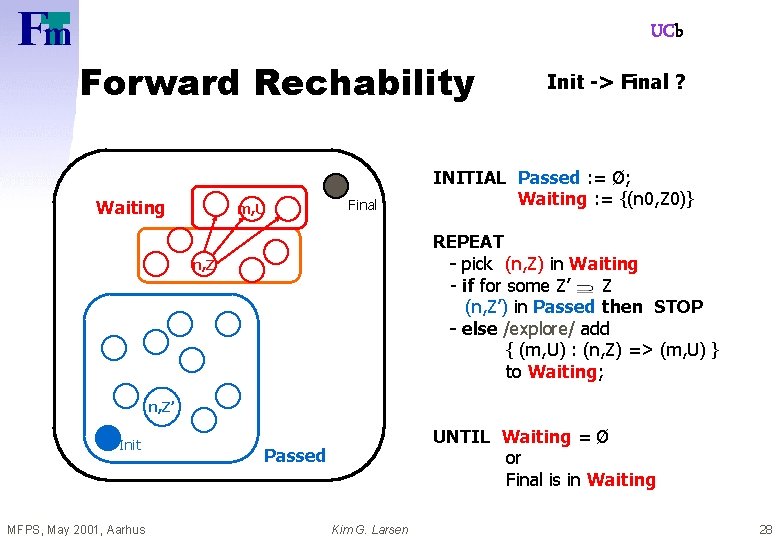
UCb Forward Rechability Final Waiting n, Z’ MFPS, May 2001, Aarhus INITIAL Passed : = Ø; Waiting : = {(n 0, Z 0)} REPEAT - pick (n, Z) in Waiting - if for some Z’ Z (n, Z’) in Passed then STOP - else (explore) add { (m, U) : (n, Z) => (m, U) } to Waiting; Add (n, Z) to Passed n, Z Init -> Final ? UNTIL Waiting = Ø or Final is in Waiting Passed Kim G. Larsen 27

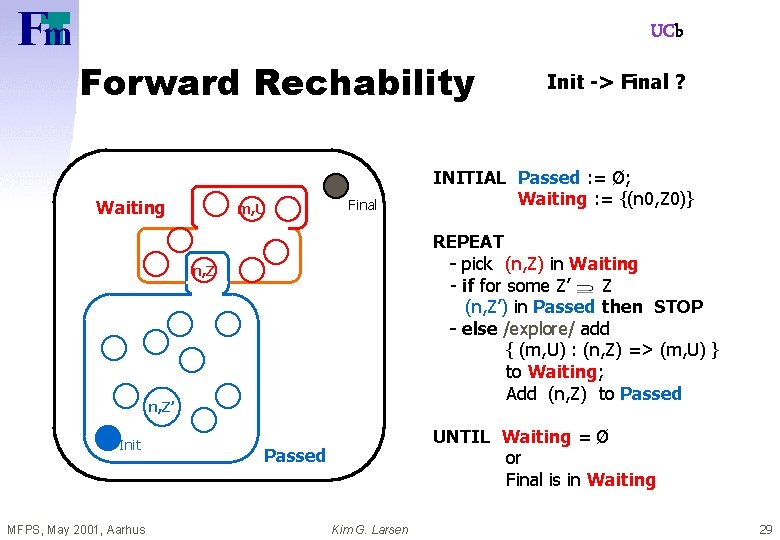
UCb Forward Rechability Waiting m, U Final n, Z’ MFPS, May 2001, Aarhus INITIAL Passed : = Ø; Waiting : = {(n 0, Z 0)} REPEAT - pick (n, Z) in Waiting - if for some Z’ Z (n, Z’) in Passed then STOP - else /explore/ add { (m, U) : (n, Z) => (m, U) } to Waiting; Add (n, Z) to Passed n, Z Init -> Final ? UNTIL Waiting = Ø or Final is in Waiting Passed Kim G. Larsen 28

UCb Forward Rechability Waiting m, U Final n, Z’ MFPS, May 2001, Aarhus INITIAL Passed : = Ø; Waiting : = {(n 0, Z 0)} REPEAT - pick (n, Z) in Waiting - if for some Z’ Z (n, Z’) in Passed then STOP - else /explore/ add { (m, U) : (n, Z) => (m, U) } to Waiting; Add (n, Z) to Passed n, Z Init -> Final ? UNTIL Waiting = Ø or Final is in Waiting Passed Kim G. Larsen 29

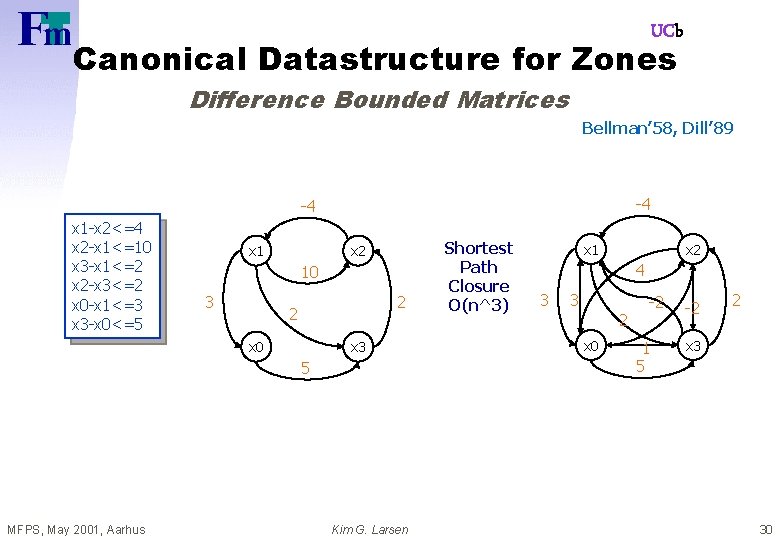
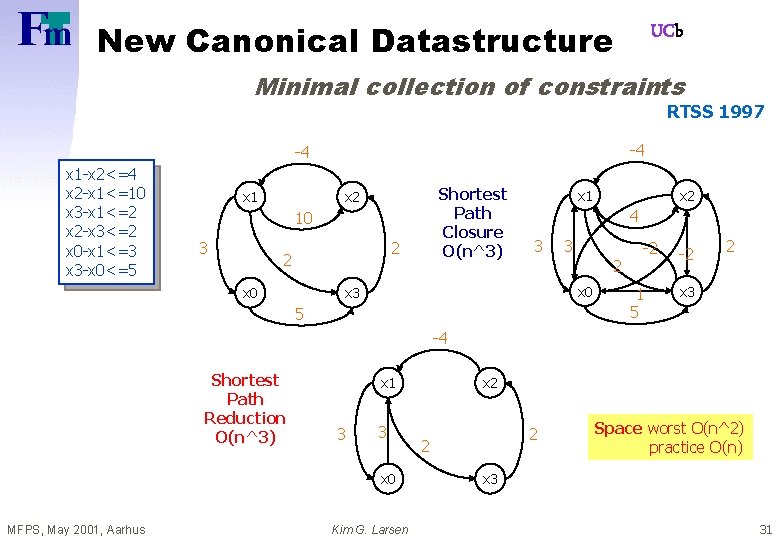
UCb Canonical Datastructure for Zones Difference Bounded Matrices Bellman’ 58, Dill’ 89 -4 -4 x 1 -x 2<=4 x 2 -x 1<=10 x 3 -x 1<=2 x 2 -x 3<=2 x 0 -x 1<=3 x 3 -x 0<=5 x 1 x 2 10 3 2 2 x 0 x 3 5 MFPS, May 2001, Aarhus Kim G. Larsen Shortest Path Closure O(n^3) x 1 x 2 4 3 3 2 x 0 -2 1 5 -2 2 x 3 30

New Canonical Datastructure UCb Minimal collection of constraints RTSS 1997 -4 -4 x 1 -x 2<=4 x 2 -x 1<=10 x 3 -x 1<=2 x 2 -x 3<=2 x 0 -x 1<=3 x 3 -x 0<=5 x 1 Shortest Path Closure O(n^3) x 2 10 3 2 2 x 0 x 1 x 2 4 3 3 2 x 0 x 3 5 -2 1 5 -2 2 x 3 -4 Shortest Path Reduction O(n^3) x 1 3 3 x 0 MFPS, May 2001, Aarhus Kim G. Larsen x 2 2 2 Space worst O(n^2) practice O(n) x 3 31

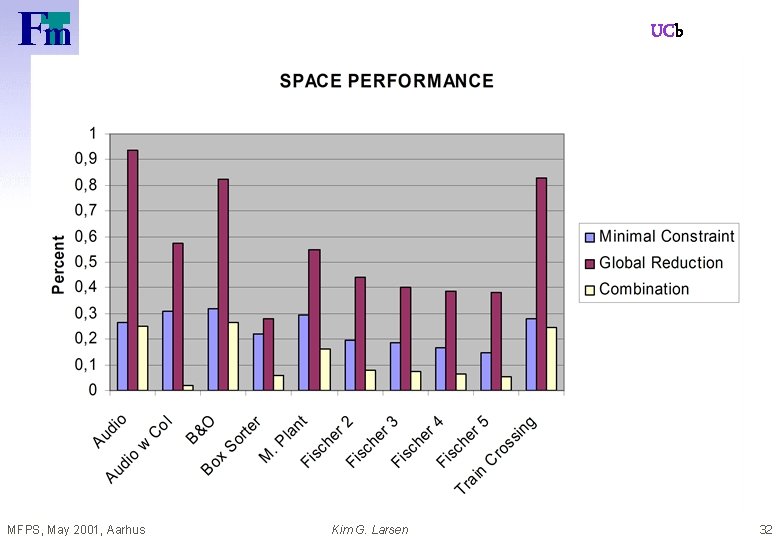
UCb MFPS, May 2001, Aarhus Kim G. Larsen 32

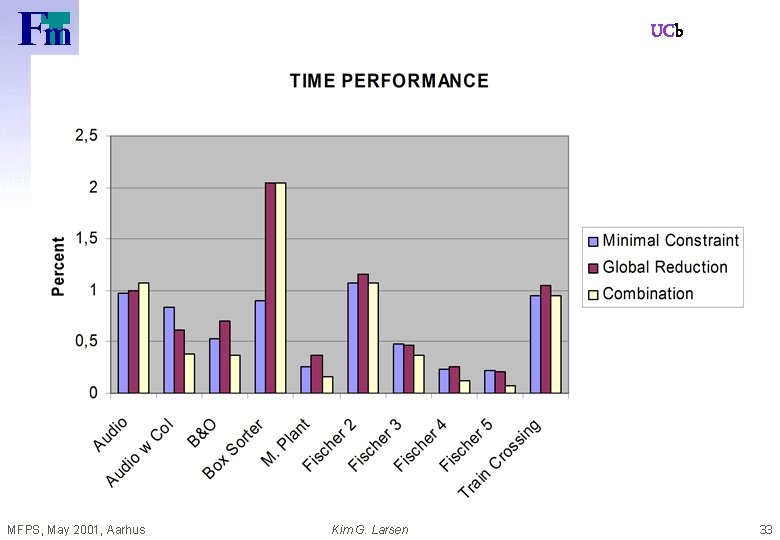
UCb MFPS, May 2001, Aarhus Kim G. Larsen 33

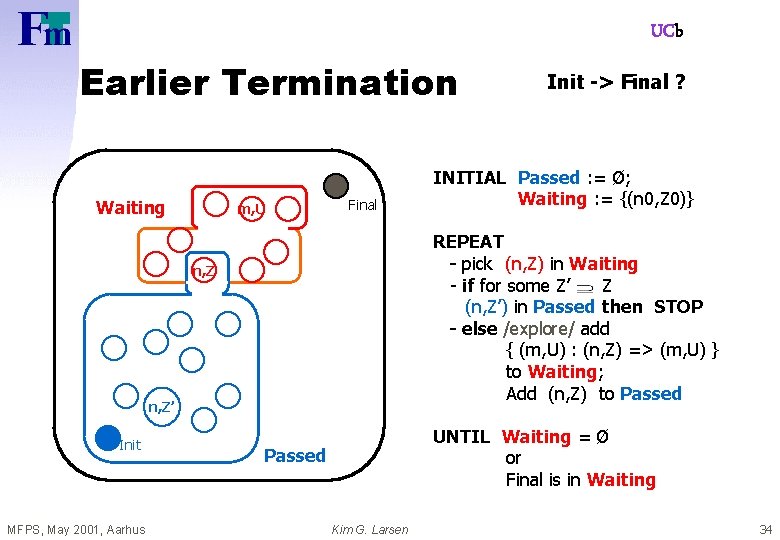
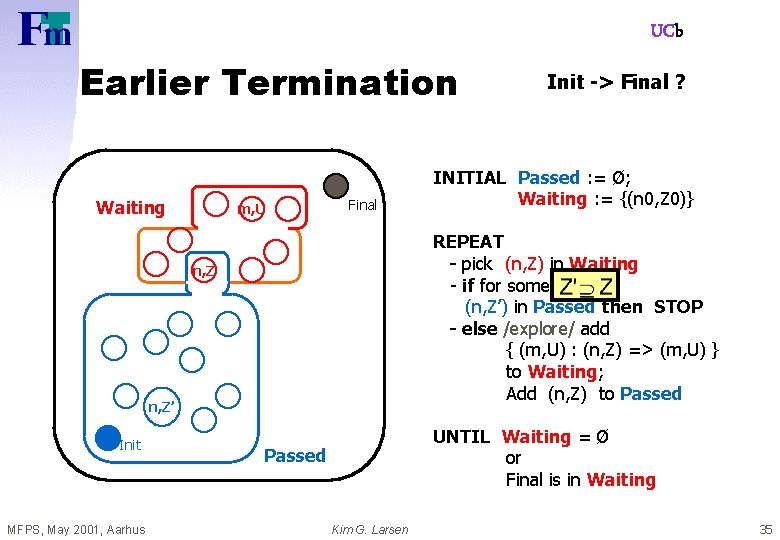
UCb Earlier Termination Waiting m, U Final n, Z’ MFPS, May 2001, Aarhus INITIAL Passed : = Ø; Waiting : = {(n 0, Z 0)} REPEAT - pick (n, Z) in Waiting - if for some Z’ Z (n, Z’) in Passed then STOP - else /explore/ add { (m, U) : (n, Z) => (m, U) } to Waiting; Add (n, Z) to Passed n, Z Init -> Final ? UNTIL Waiting = Ø or Final is in Waiting Passed Kim G. Larsen 34

UCb Earlier Termination Waiting m, U Final n, Z’ MFPS, May 2001, Aarhus INITIAL Passed : = Ø; Waiting : = {(n 0, Z 0)} REPEAT - pick (n, Z) in Waiting - if for some Z’ Z (n, Z’) in Passed then STOP - else /explore/ add { (m, U) : (n, Z) => (m, U) } to Waiting; Add (n, Z) to Passed n, Z Init -> Final ? UNTIL Waiting = Ø or Final is in Waiting Passed Kim G. Larsen 35

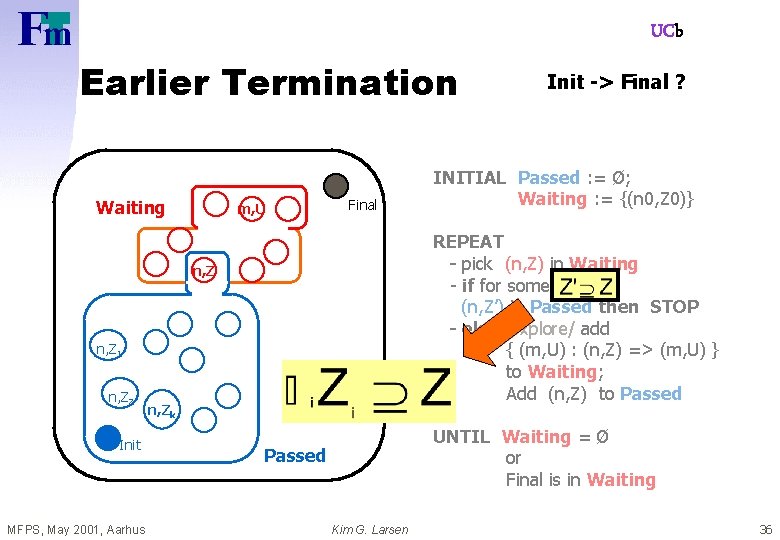
UCb Earlier Termination Waiting m, U Final n, Z 1 Init MFPS, May 2001, Aarhus INITIAL Passed : = Ø; Waiting : = {(n 0, Z 0)} REPEAT - pick (n, Z) in Waiting - if for some (n, Z’) in Passed then STOP - else /explore/ add { (m, U) : (n, Z) => (m, U) } to Waiting; Add (n, Z) to Passed n, Z 2 Init -> Final ? n, Zk UNTIL Waiting = Ø or Final is in Waiting Passed Kim G. Larsen 36

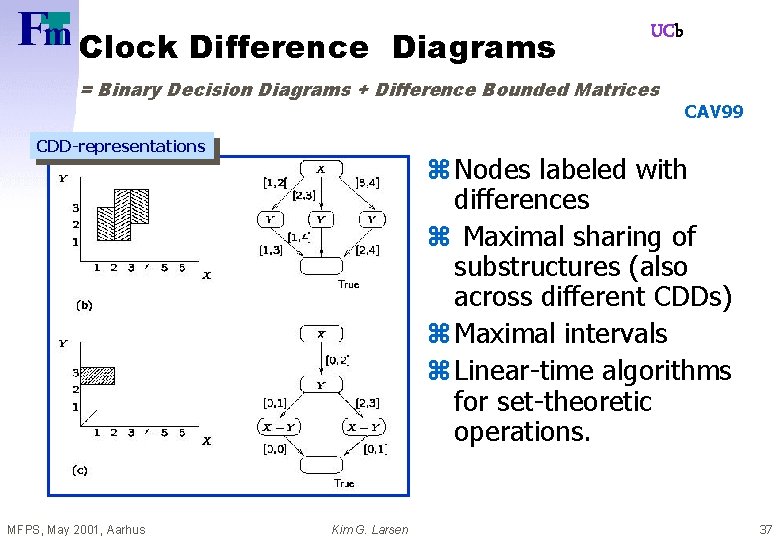
Clock Difference Diagrams UCb = Binary Decision Diagrams + Difference Bounded Matrices CDD-representations MFPS, May 2001, Aarhus CAV 99 z Nodes labeled with differences z Maximal sharing of substructures (also across different CDDs) z Maximal intervals z Linear-time algorithms for set-theoretic operations. Kim G. Larsen 37

UCb MFPS, May 2001, Aarhus Kim G. Larsen 38

UCb MFPS, May 2001, Aarhus Kim G. Larsen 39

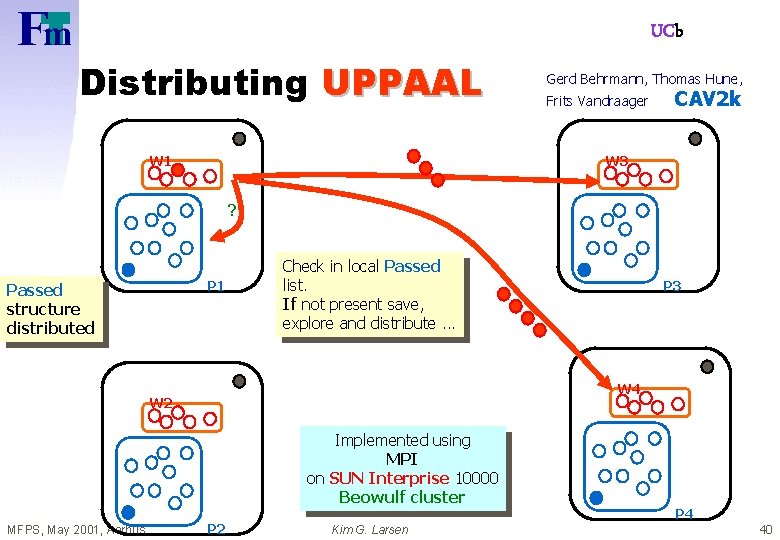
UCb Distributing UPPAAL Gerd Behrmann, Thomas Hune, Frits Vandraager CAV 2 k W 3 W 1 ? P 1 Passed structure distributed Check in local Passed list. If not present save, explore and distribute. . . W 4 W 2 Implemented using MPI on SUN Interprise 10000 Beowulf cluster MFPS, May 2001, Aarhus P 3 P 2 Kim G. Larsen P 4 40

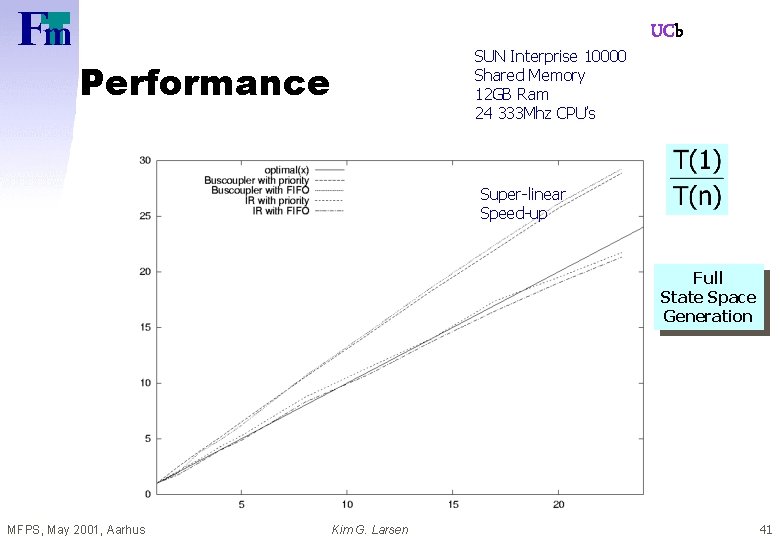
SUN Interprise 10000 Shared Memory 12 GB Ram 24 333 Mhz CPU’s Performance UCb Super-linear Speed-up Full State Space Generation MFPS, May 2001, Aarhus Kim G. Larsen 41

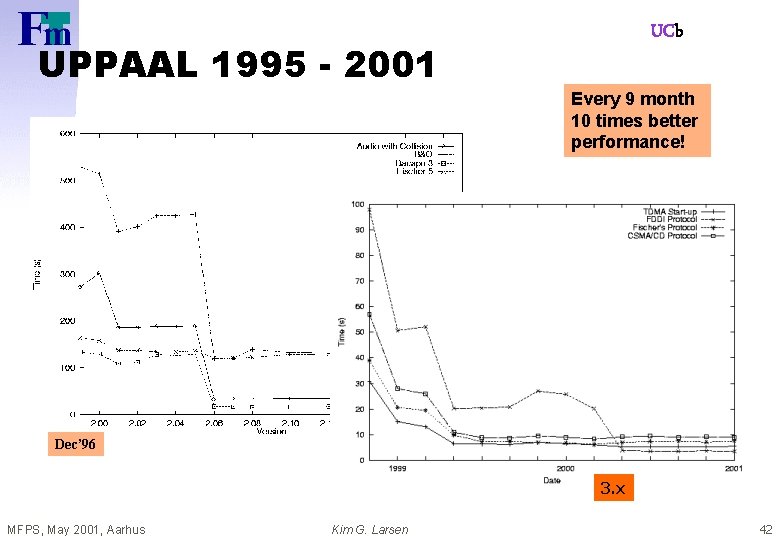
UCb UPPAAL 1995 - 2001 Every 9 month 10 times better performance! Dec’ 96 Sep’ 98 3. x MFPS, May 2001, Aarhus Kim G. Larsen 42

Formal methods & Tools m al i t p o CUPPAAL Scheduling & Synthesis of Control Programs w Gerd Behrman, Ed Brinksma, Ansgar Fehnker, Thomas Hune, Paul Pettersson, Judi Romijn, Frits Vaandrager …, HSCC’ 01, TACAS’ 01, CAV’ 01 UCb

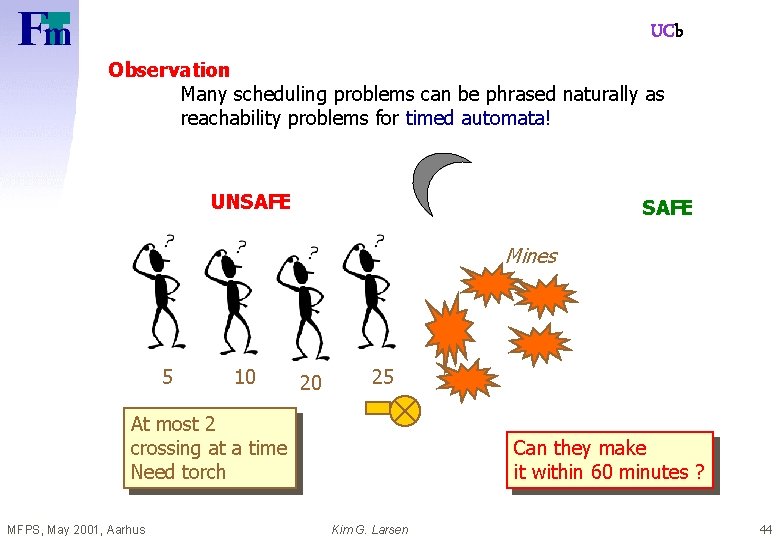
UCb Observation Many scheduling problems can be phrased naturally as reachability problems for timed automata! UNSAFE Mines 5 10 20 25 At most 2 crossing at a time Need torch MFPS, May 2001, Aarhus Can they make it within 60 minutes ? Kim G. Larsen 44

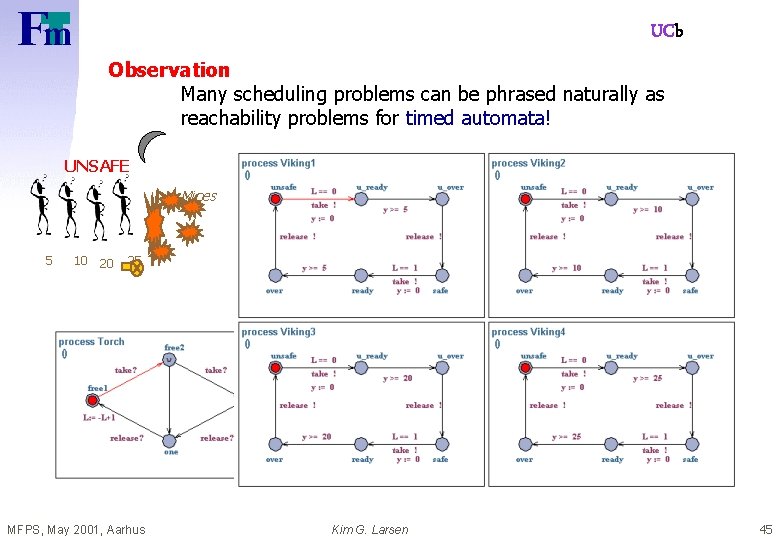
UCb Observation Many scheduling problems can be phrased naturally as reachability problems for timed automata! UNSAFE Mines 5 10 20 25 MFPS, May 2001, Aarhus Kim G. Larsen 45

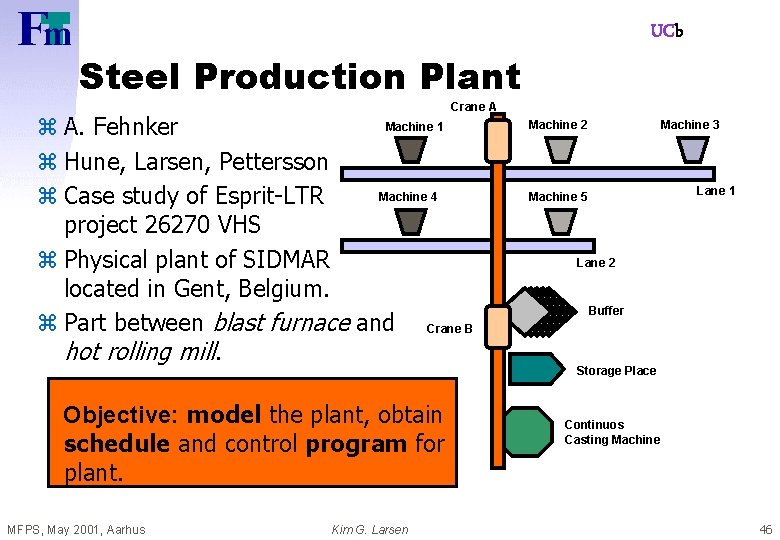
UCb Steel Production Plant Crane A Machine 1 z A. Fehnker z Hune, Larsen, Pettersson Machine 4 z Case study of Esprit-LTR project 26270 VHS z Physical plant of SIDMAR located in Gent, Belgium. z Part between blast furnace and Crane B hot rolling mill. Objective: model the plant, obtain schedule and control program for plant. MFPS, May 2001, Aarhus Kim G. Larsen Machine 2 Machine 3 Lane 1 Machine 5 Lane 2 Buffer Storage Place Continuos Casting Machine 46

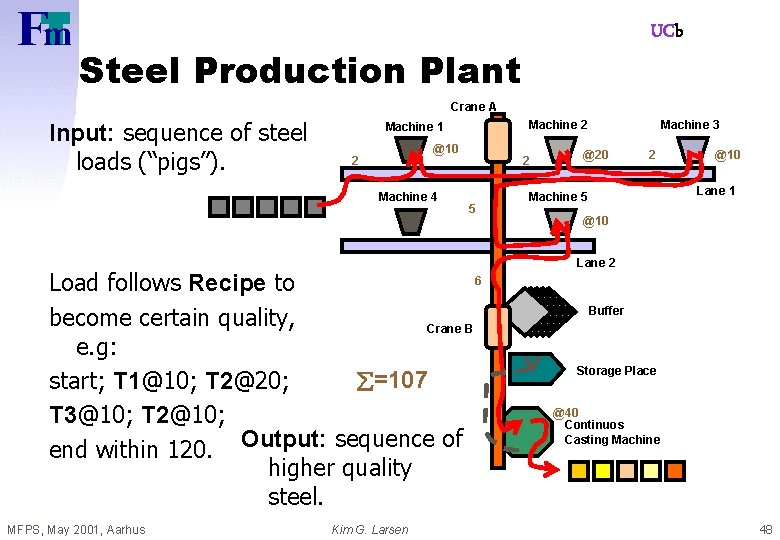
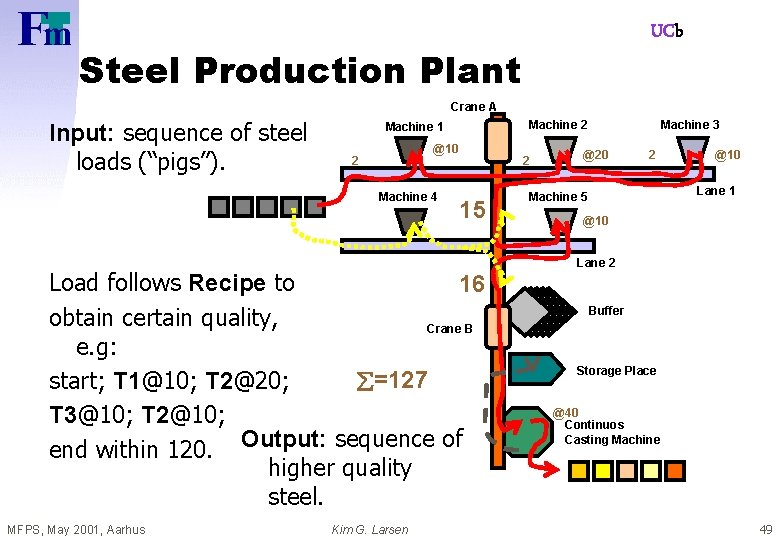
UCb Steel Production Plant Crane A Input: sequence of steel loads (“pigs”). Machine 1 Machine 4 Load follows Recipe to become certain quality, Crane B e. g: start; T 1@10; T 2@20; T 3@10; T 2@10; end within 120. Output: sequence of higher quality steel. MFPS, May 2001, Aarhus Kim G. Larsen Machine 2 Machine 3 Lane 1 Machine 5 Lane 2 Buffer Storage Place Continuos Casting Machine 47

UCb Steel Production Plant Crane A Input: sequence of steel loads (“pigs”). Machine 2 Machine 1 @10 2 Machine 4 2 5 6 Load follows Recipe to become certain quality, Crane B e. g: =107 start; T 1@10; T 2@20; T 3@10; T 2@10; end within 120. Output: sequence of higher quality steel. MFPS, May 2001, Aarhus Kim G. Larsen Machine 3 @20 2 @10 Lane 1 Machine 5 @10 Lane 2 Buffer Storage Place @40 Continuos Casting Machine 48

UCb Steel Production Plant Crane A Input: sequence of steel loads (“pigs”). Machine 2 Machine 1 @10 2 Machine 4 2 15 Load follows Recipe to 16 obtain certain quality, Crane B e. g: =127 start; T 1@10; T 2@20; T 3@10; T 2@10; end within 120. Output: sequence of higher quality steel. MFPS, May 2001, Aarhus Kim G. Larsen Machine 3 @20 2 @10 Lane 1 Machine 5 @10 Lane 2 Buffer Storage Place @40 Continuos Casting Machine 49

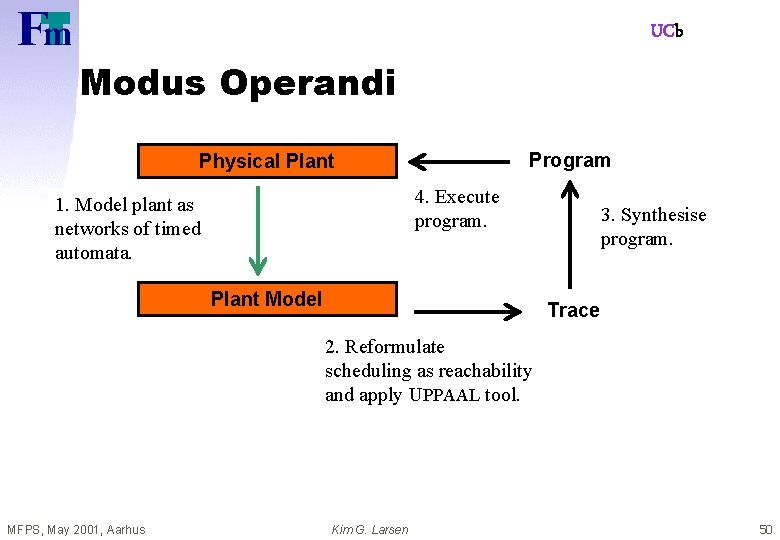
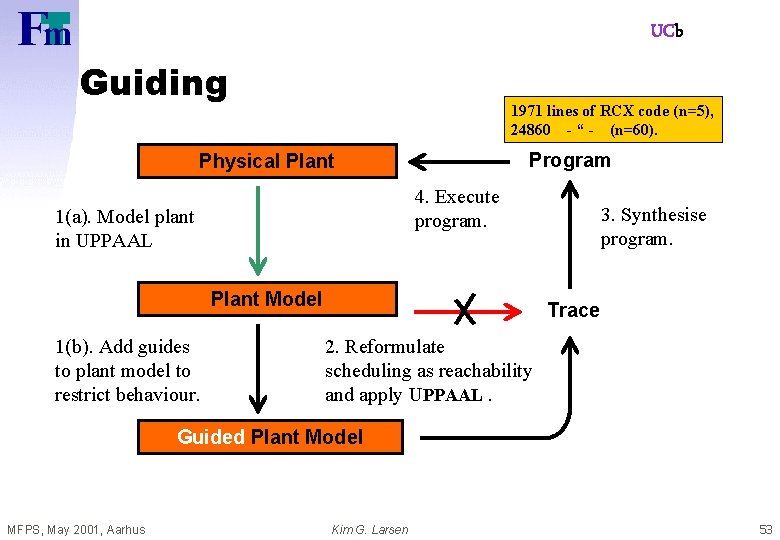
UCb Modus Operandi Program Physical Plant 4. Execute program. 1. Model plant as networks of timed automata. Plant Model 3. Synthesise program. Trace 2. Reformulate scheduling as reachability and apply UPPAAL tool. MFPS, May 2001, Aarhus Kim G. Larsen 50

UCb A single load (part of) MFPS, May 2001, Aarhus Kim G. Larsen Crane B 51

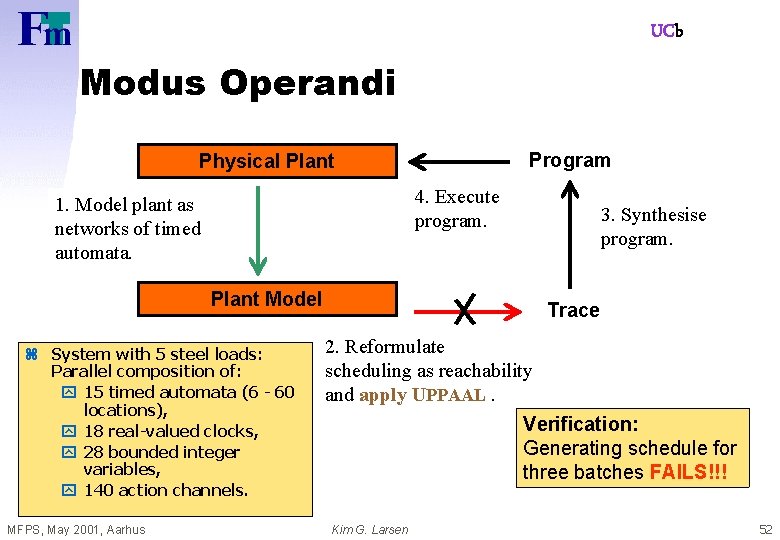
UCb Modus Operandi Program Physical Plant 4. Execute program. 1. Model plant as networks of timed automata. 3. Synthesise program. Plant Model z System with 5 steel loads: Parallel composition of: y 15 timed automata (6 - 60 locations), y 18 real-valued clocks, y 28 bounded integer variables, y 140 action channels. MFPS, May 2001, Aarhus Trace 2. Reformulate scheduling as reachability and apply UPPAAL. Verification: Generating schedule for three batches FAILS!!! Kim G. Larsen 52

UCb Guiding 1971 lines of RCX code (n=5), 24860 - “ - (n=60). Program Physical Plant 4. Execute program. 1(a). Model plant in UPPAAL Plant Model 1(b). Add guides to plant model to restrict behaviour. 3. Synthesise program. Trace 2. Reformulate scheduling as reachability and apply UPPAAL. Guided Plant Model MFPS, May 2001, Aarhus Kim G. Larsen 53

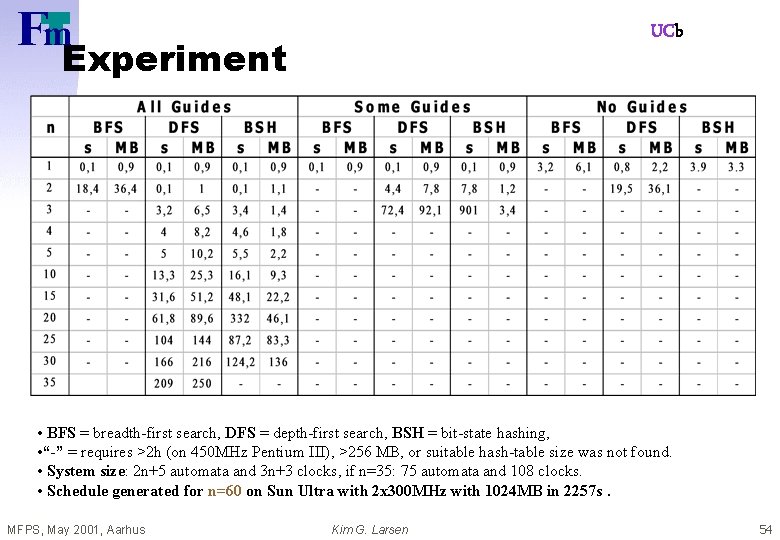
UCb Experiment • BFS = breadth-first search, DFS = depth-first search, BSH = bit-state hashing, • “-” = requires >2 h (on 450 MHz Pentium III), >256 MB, or suitable hash-table size was not found. • System size: 2 n+5 automata and 3 n+3 clocks, if n=35: 75 automata and 108 clocks. • Schedule generated for n=60 on Sun Ultra with 2 x 300 MHz with 1024 MB in 2257 s. MFPS, May 2001, Aarhus Kim G. Larsen 54

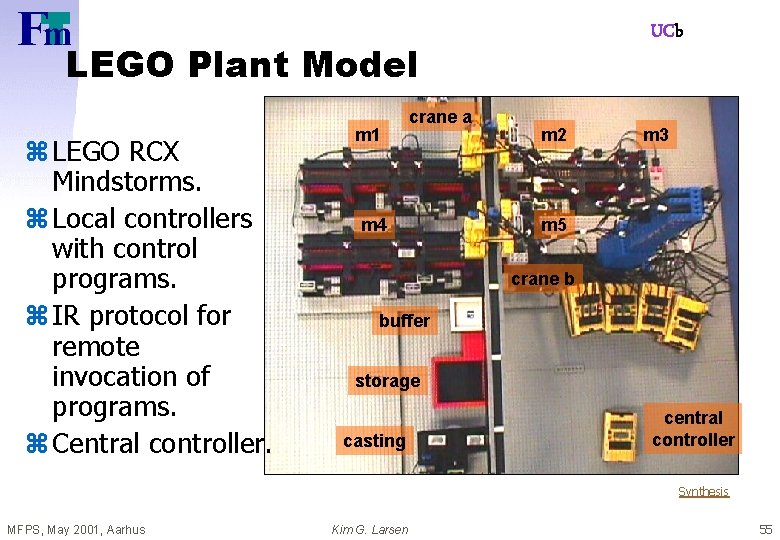
UCb LEGO Plant Model z LEGO RCX Mindstorms. z Local controllers with control programs. z IR protocol for remote invocation of programs. z Central controller. m 1 crane a m 4 m 2 m 3 m 5 crane b buffer storage casting central controller Synthesis MFPS, May 2001, Aarhus Kim G. Larsen 55

LEGO Plant Model UCb Belt/Machine Unit. MFPS, May 2001, Aarhus Kim G. Larsen 56

UCb Time Optimality z Asarin & Maler (1999) Time optimal control using backwards fixed point computation z Niebert, Tripakis & Yovine (2000) Minimum-time reachability using forward reachability z Behrmann, Fehnker et all [TACAS 01, MBVI 01] Minimum-time reachability using Branch-and-Bound MFPS, May 2001, Aarhus Kim G. Larsen 57

UCb Cost Optimality z In scheduling theory one is not just interested in shortest or fastest schedules; also other cost functions are considered. z This leads us to introduce a model of Linear Priced Timed Automata which adds prices to locations and transitions z Price of a transition: z Price of a location: MFPS, May 2001, Aarhus The cost of taking it. The cost per time unit of staying there. Kim G. Larsen 58

Formal methods & Tools Linearly Priced Timed Automata UCb

UCb Example MFPS, May 2001, Aarhus Prices Kim G. Larsen 60

UCb Example (execution) MFPS, May 2001, Aarhus Kim G. Larsen 61

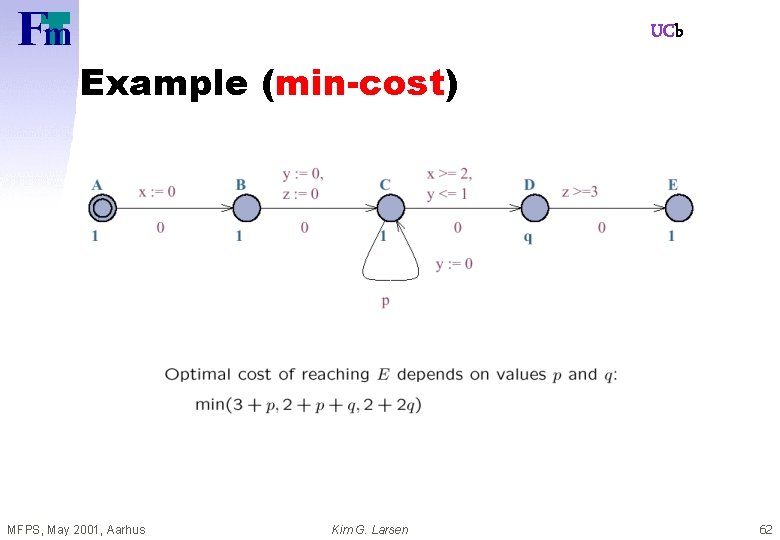
UCb Example (min-cost) MFPS, May 2001, Aarhus Kim G. Larsen 62

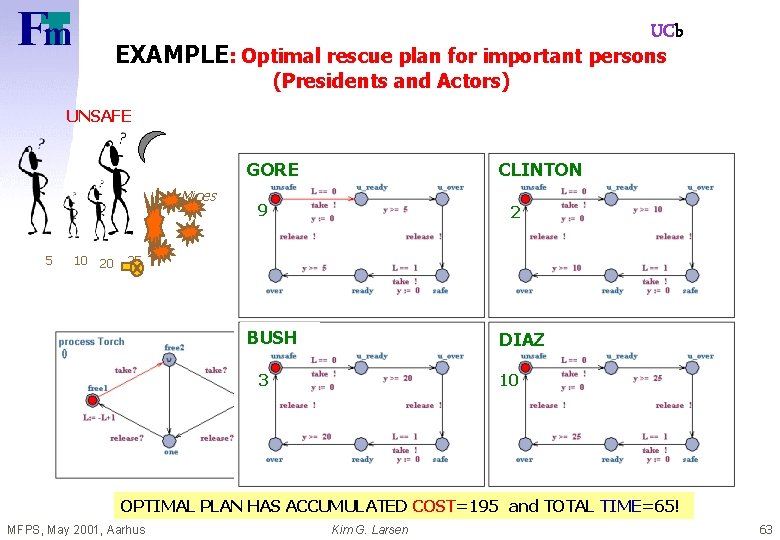
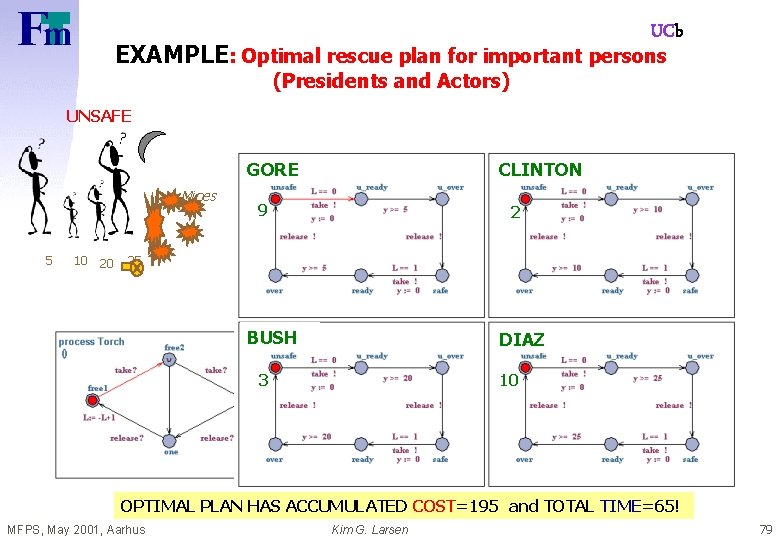
UCb EXAMPLE: Optimal rescue plan for important persons (Presidents and Actors) UNSAFE GORE Mines 5 10 20 CLINTON 9 2 25 BUSH DIAZ 3 10 OPTIMAL PLAN HAS ACCUMULATED COST=195 and TOTAL TIME=65! MFPS, May 2001, Aarhus Kim G. Larsen 63

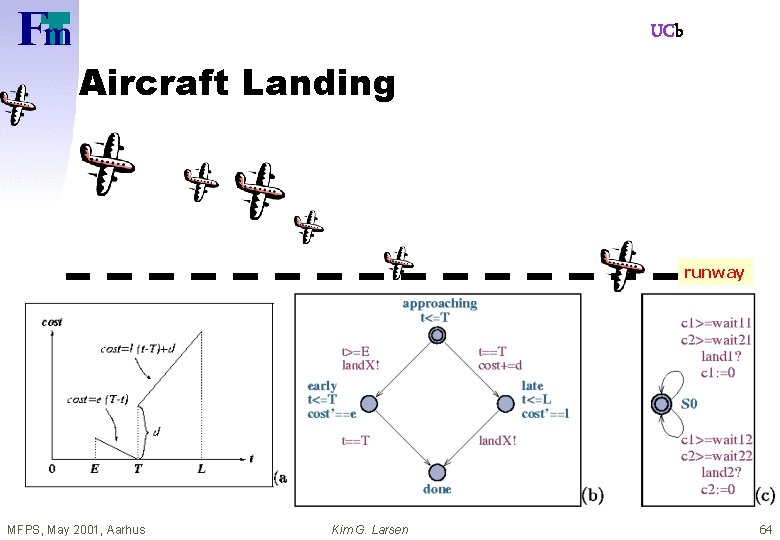
UCb Aircraft Landing runway MFPS, May 2001, Aarhus Kim G. Larsen 64

Formal methods & Tools Priced Zones Efficient Computability of Minimum Cost Reachability UCb

UCb Zones y Operations Z x MFPS, May 2001, Aarhus Kim G. Larsen 66

UCb Priced Zone y Z 2 4 -1 x MFPS, May 2001, Aarhus Kim G. Larsen 67

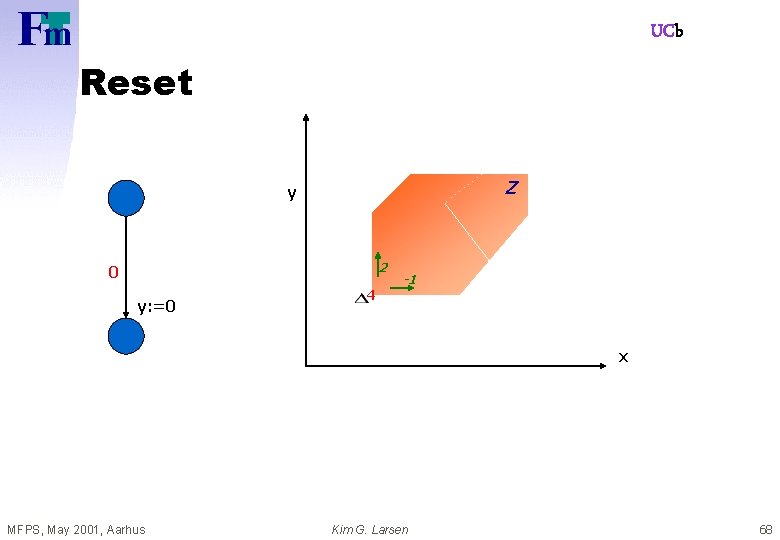
UCb Reset Z y 2 0 y: =0 4 -1 x MFPS, May 2001, Aarhus Kim G. Larsen 68

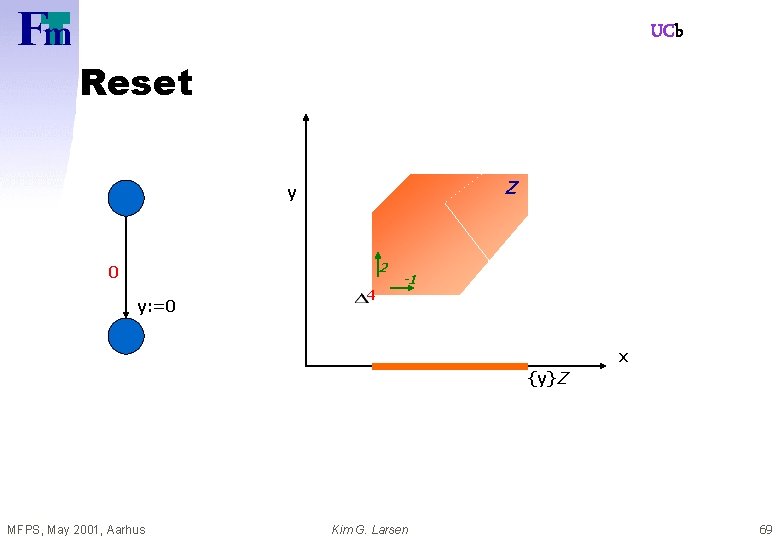
UCb Reset Z y 2 0 y: =0 4 -1 x {y}Z MFPS, May 2001, Aarhus Kim G. Larsen 69

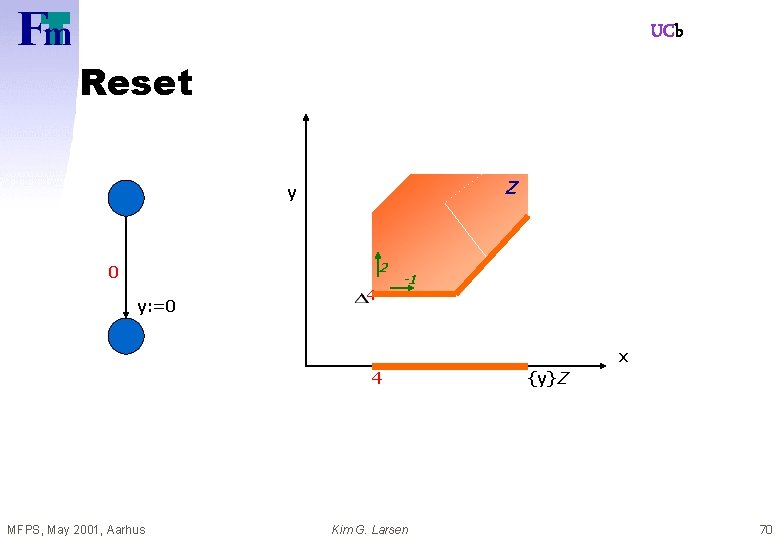
UCb Reset Z y 2 0 y: =0 4 -1 x 4 MFPS, May 2001, Aarhus Kim G. Larsen {y}Z 70

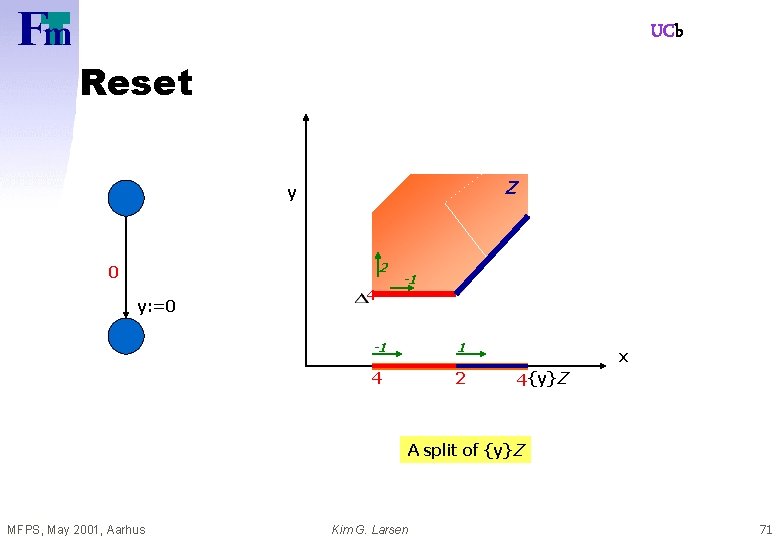
UCb Reset Z y 2 0 y: =0 4 -1 -1 1 4 2 x 4 {y}Z A split of {y}Z MFPS, May 2001, Aarhus Kim G. Larsen 71

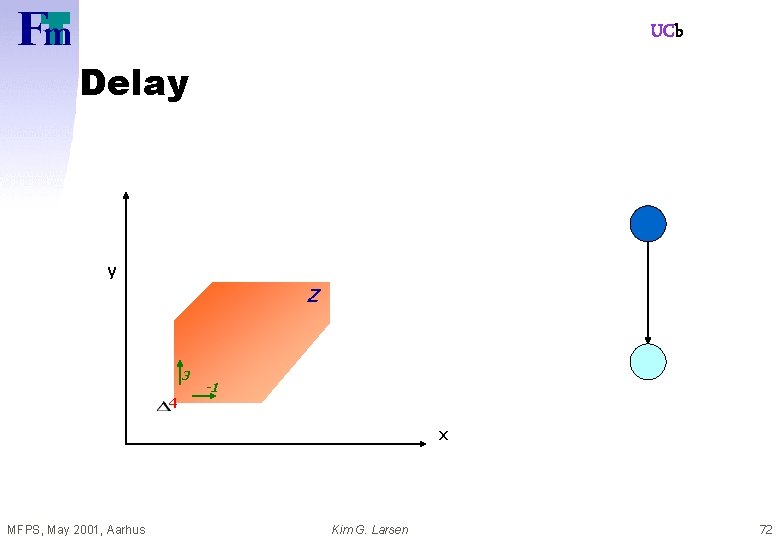
UCb Delay y Z 3 4 -1 x MFPS, May 2001, Aarhus Kim G. Larsen 72

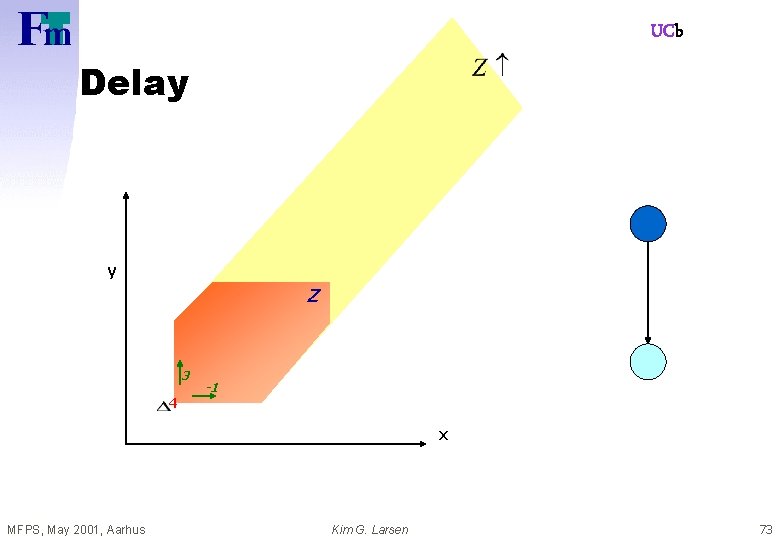
UCb Delay y Z 3 4 -1 x MFPS, May 2001, Aarhus Kim G. Larsen 73

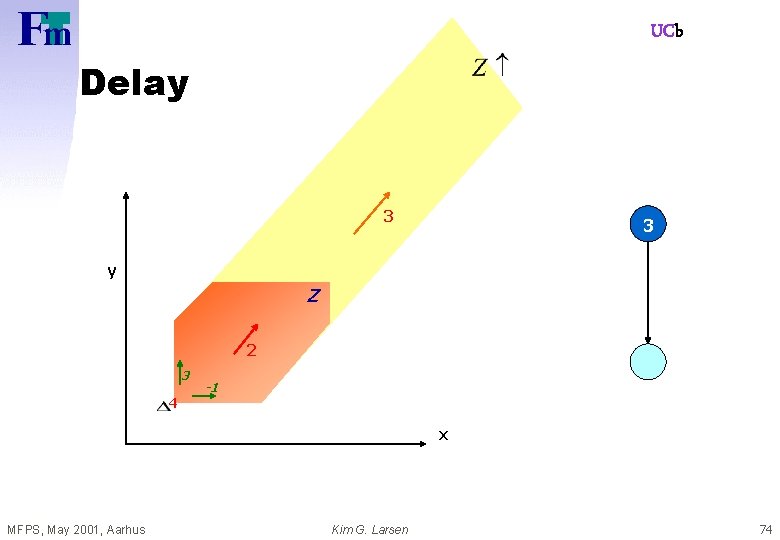
UCb Delay 3 3 y Z 2 3 4 -1 x MFPS, May 2001, Aarhus Kim G. Larsen 74

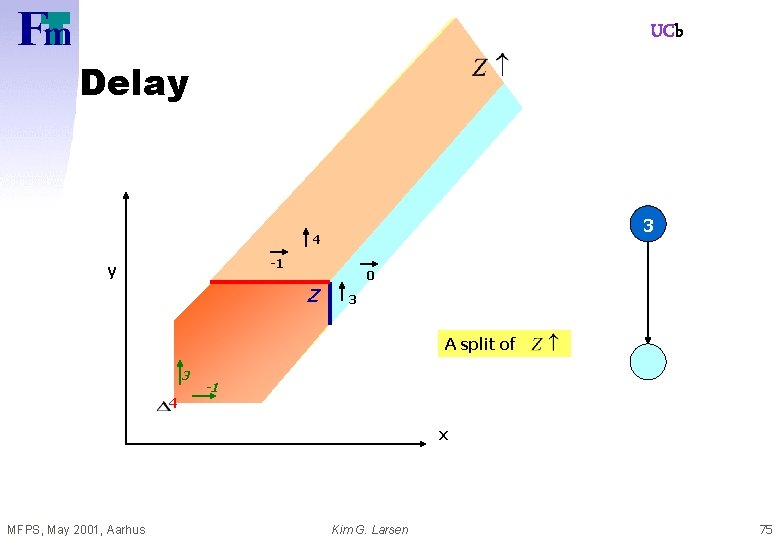
UCb Delay 3 4 -1 y 0 Z 3 A split of 3 4 -1 x MFPS, May 2001, Aarhus Kim G. Larsen 75

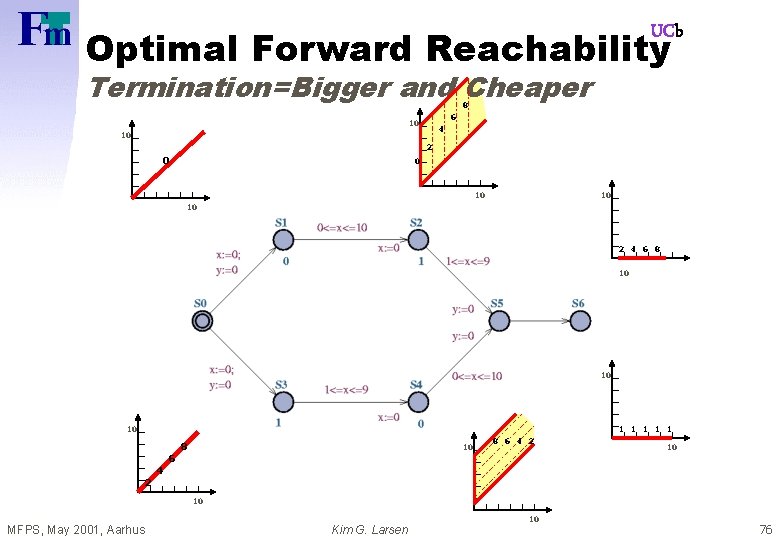
UCb Optimal Forward Reachability Termination=Bigger and Cheaper 8 6 10 4 10 2 0 0 10 10 10 2 4 6 8 10 10 10 1 1 1 2 4 6 8 10 8 6 4 2 10 10 MFPS, May 2001, Aarhus Kim G. Larsen 10 76

UCb Branch & Bound Algorithm Selection may be Guided Exploration may be Pruned MFPS, May 2001, Aarhus Kim G. Larsen 77

Formal methods & Tools Experiments UCb

UCb EXAMPLE: Optimal rescue plan for important persons (Presidents and Actors) UNSAFE GORE Mines 5 10 20 CLINTON 9 2 25 BUSH DIAZ 3 10 OPTIMAL PLAN HAS ACCUMULATED COST=195 and TOTAL TIME=65! MFPS, May 2001, Aarhus Kim G. Larsen 79

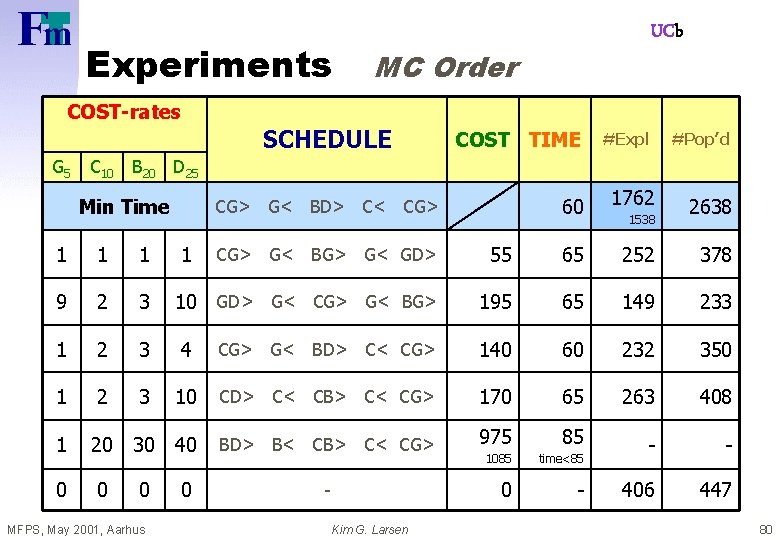
Experiments UCb MC Order COST-rates SCHEDULE G 5 C 10 COST TIME #Expl #Pop’d B 20 D 25 Min Time CG> G< BD> C< CG> 60 1762 1538 2638 1 1 CG> G< BG> G< GD> 55 65 252 378 9 2 3 10 GD> G< CG> G< BG> 195 65 149 233 1 2 3 4 CG> G< BD> C< CG> 140 60 232 350 1 2 3 10 CD> C< CB> C< CG> 170 65 263 408 1 20 30 40 BD> B< CB> C< CG> 975 85 1085 time<85 - - 0 0 - 0 - 406 447 MFPS, May 2001, Aarhus Kim G. Larsen 80

UCb Aircraft Landing MFPS, May 2001, Aarhus Kim G. Larsen Source of examples: Baesley et al’ 2000 81

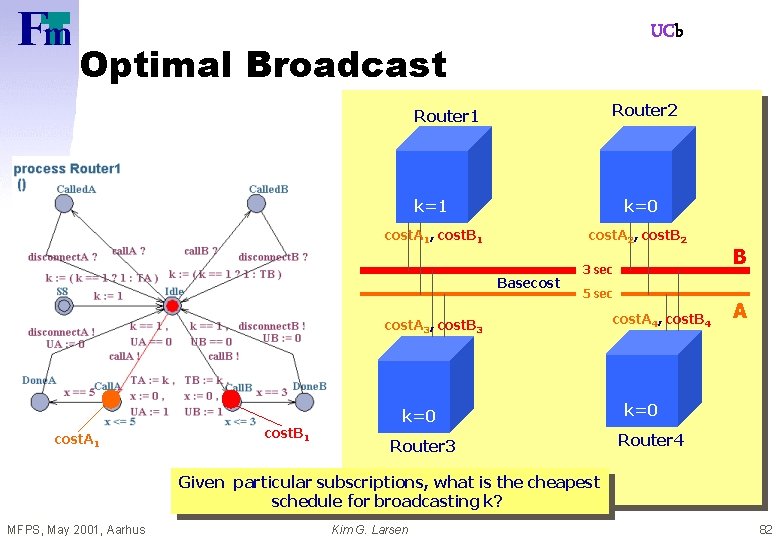
UCb Optimal Broadcast Router 2 Router 1 k=0 cost. A 1, cost. B 1 cost. A 2, cost. B 2 Basecost 3 sec 5 sec cost. A 3, cost. B 3 cost. A 1 cost. B 1 k=0 Router 3 cost. A 4, cost. B 4 B A k=0 Router 4 Given particular subscriptions, what is the cheapest schedule for broadcasting k? MFPS, May 2001, Aarhus Kim G. Larsen 82

UCb Experimental Results COST-rates BC R 1 R 2 R 3 R 4 Min Time 0 SCHEDULE COST 1>3(B) ; ( 3>4(B) | 1>2(A) ) TIME #Expl 8 1016 1>4(A) ; 3>4(A) ; 4>2(A) 15 15 2982 3 1>3(B) ; ( 3>4(B) | 1>2(A) ) 47 8 1794 0 1>3(A) ; 3>2(A) ; 3>4(A) 60 15 665 3 1>4(A) ; 4>3(B) ; 4>2(B) 95 11 571 1>4(B) ; ( 1>3(A) | 4>2(B) ) 946 8 1471 1>4(B) ; 4>2(B) ; 4>3(B) 102 9 1167 1>4(B) ; ( 1>3(A) | 4>2(B) ) 146 8 1688 100 1: 3 10 : 30 1: 3 5 1: 3 6: 2 : 15 0 t<=10 0 t<=8 MFPS, May 2001, Aarhus Kim G. Larsen 83

UCb Current & Future Research z DUPPAAL z GUPPAAL z CUPPAAL z z Pr. UPPAAL z PUPPAAL z Hy. UPPAAL MFPS, May 2001, Aarhus Kim G. Larsen 84

UCb Current & Future Research z DUPPAAL z GUPPAAL z CUPPAAL Distributed Guided Cost-Optimal z Pr. UPPAAL z PUPPAAL z Hy. UPPAAL Probabilistic Parameterized Hierarchical (UML) Hybrid (stopwatch automata) MFPS, May 2001, Aarhus Kim G. Larsen 85

Conclusion & Future UCb z New method for solving and modeling optimal scheduling/planning problems. z Advantages: y. Easy, flexible and very expressive modeling w clear operational interpretation y. Several, small LP problems. z Disadvantages: yexisting approaches still somewhat better z Goals: y. Integrate Model Checking and Scheduling. y. Extension to (optimal) dynamic scheduling/controller synthesis. MFPS, May 2001, Aarhus Kim G. Larsen 86

CONCUR Conference 21. -24. August, Aalborg, DK Invited Speakers Prof. Bengt Jonsson (Feature Interaction) Prof. Robin Milner (Turing Award winner) Prof. Shankar Sastry (Hybrid Systems) Prof. Steve Schneider (Security) UCb Satelite Workshops Express Workshop Get. Co Testing Workshop Safety Critical Systems Real. Time Tools Workshop Tutorials Holger Hermans, Joost-Pieter Katoen (Performance) John Hatcliff (Model. Checking C-programs) concur 0 1. cs. auc MFPS, May 2001, Aarhus CALL-FOR-PAPERS . dk March 25 Kim G. Larsen 87

Formal methods & Tools Thank you for the attention For more information http: //www. uppaal. com UCb