Forces interatomic interactions electrostatic Coulombs law dielectric constant

Forces • inter-atomic interactions – – – – electrostatic - Coulomb's law, dielectric constant hydrogen-bonds charge-dipole, dipole-quadrapole polarizability van der Waals, London dispersion (stickiness) cation-pi (Arg/Lys to aromatic) aromatic ring-stacking (Phe, Tyr, Trp, His) • hydrophobic effect – driving force • enthalpy balanced against entropy – DG=DH-TDS – DH adds contributions from 100 s of interactions at ~1 kcal/mol each – yet net stability of proteins is often DG ~ 15 kcal/mol

Electrostatic Interactions • formal charges – Arg, Lys: +1 – Asp, Glu: -1 – His=0 or +1? • Coulomb’s law, range • dielectric constant – water: = 80 – vacuum: = 1 – protein interior: = 2 -4? (due to dipoles) • solvent screening, ionic strength • salt bridges in proteins – strength: ~1 kcal/mol (Horowitz et al. , 1990) (desolvation effects) • (later: potential surface calculation, Poisson. Boltzmann equation) Warshel, Russell, and Churg (1984) • without solvation effects, lone ionized groups would be highly unfavorable to bury in non-polar environments, and salt bridges would predominate folding with DG=~-30 kcal/mol • with “self-energy”, DG=~1 -4 kcal/mol

p. Ka estimation (protonation state) • ionizable residues: Arg, Lys, Asp, Glu, His, Nterm, Cterm • Cys, Tyr can also get deprotonated • H++: solve Poisson-Boltzmann equation – protonation state depends on energy of charge presence in local electrostatic potential field – reflects neighboring charges, solvent accessibility – self-energy (Warshel et al. , 1984) • • Henderson-Hasselbach equation interactions between sites Monte Carlo search (Beroza et al 1991) Onufriev, Case & Ullman (2001) – can do orthogontal transform to identify independently titrating pseudo-sites • conformational changes (Marilyn Gunner) – it helps if side-chains can reorient two interacting sites with intrinsic p. Ka’s of 7. 0 and 7. 1

• empirical rules (Li, Robertson, Jensen, 2005) – – p. Ka = model + adjustments 1. hydrogen-bonds 2. solvent exposure 3. nearby charges • iterative search: deprotonate side-chain with lowest p. Ka first, then determine effect on rest. . . PROPKA

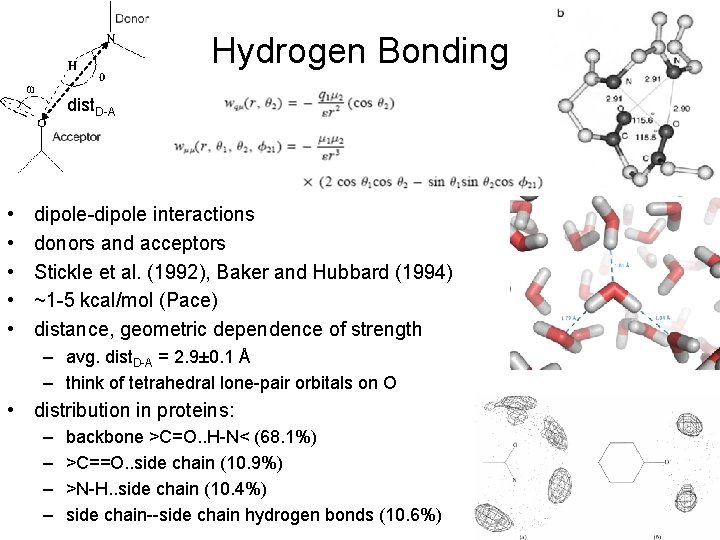
Hydrogen Bonding dist. D-A • • • dipole-dipole interactions donors and acceptors Stickle et al. (1992), Baker and Hubbard (1994) ~1 -5 kcal/mol (Pace) distance, geometric dependence of strength – avg. dist. D-A = 2. 9± 0. 1 Å – think of tetrahedral lone-pair orbitals on O • distribution in proteins: – – backbone >C=O. . H-N< (68. 1%) >C==O. . side chain (10. 9%) >N-H. . side chain (10. 4%) side chain--side chain hydrogen bonds (10. 6%)

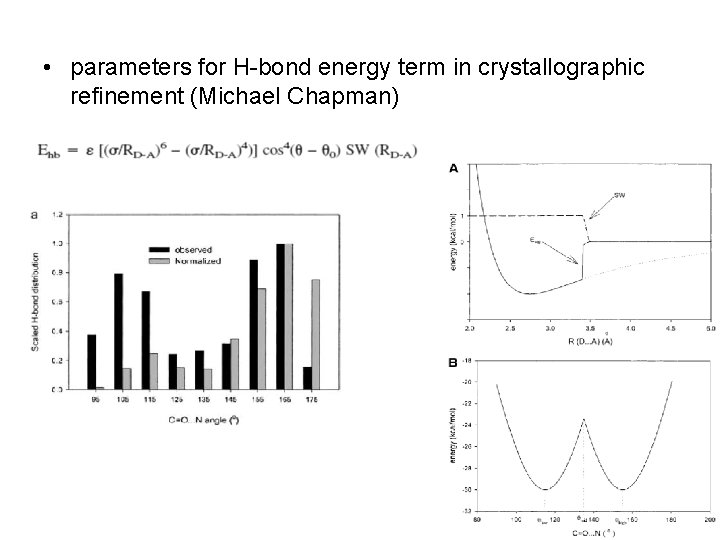
• parameters for H-bond energy term in crystallographic refinement (Michael Chapman)

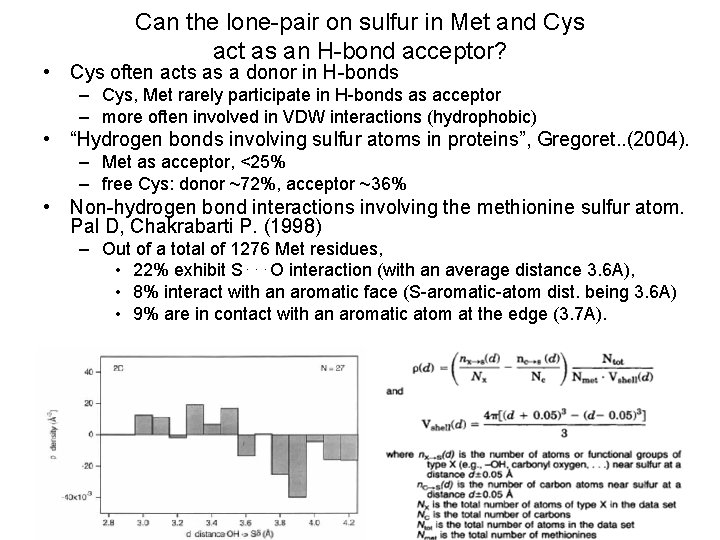
Can the lone-pair on sulfur in Met and Cys act as an H-bond acceptor? • Cys often acts as a donor in H-bonds – Cys, Met rarely participate in H-bonds as acceptor – more often involved in VDW interactions (hydrophobic) • “Hydrogen bonds involving sulfur atoms in proteins”, Gregoret. . (2004). – Met as acceptor, <25% – free Cys: donor ~72%, acceptor ~36% • Non-hydrogen bond interactions involving the methionine sulfur atom. Pal D, Chakrabarti P. (1998) – Out of a total of 1276 Met residues, • 22% exhibit S⋅⋅⋅O interaction (with an average distance 3. 6 A), • 8% interact with an aromatic face (S-aromatic-atom dist. being 3. 6 A) • 9% are in contact with an aromatic atom at the edge (3. 7 A).

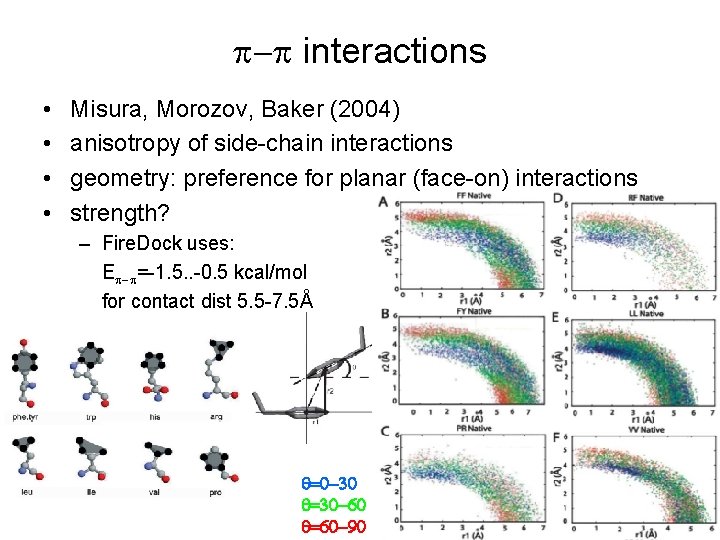
p-p interactions • • Misura, Morozov, Baker (2004) anisotropy of side-chain interactions geometry: preference for planar (face-on) interactions strength? – Fire. Dock uses: Ep-p=-1. 5. . -0. 5 kcal/mol for contact dist 5. 5 -7. 5Å q=0 -30 q=30 -60 q=60 -90

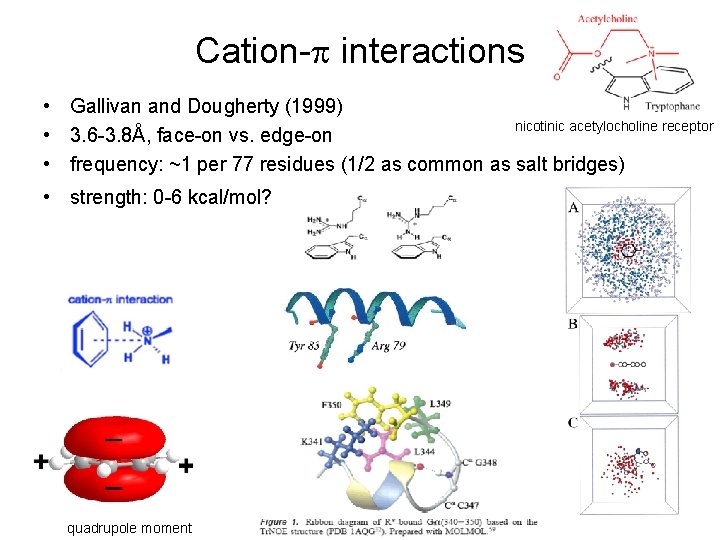
Cation-p interactions • Gallivan and Dougherty (1999) nicotinic acetylocholine receptor • 3. 6 -3. 8Å, face-on vs. edge-on • frequency: ~1 per 77 residues (1/2 as common as salt bridges) • strength: 0 -6 kcal/mol? quadrupole moment

VDW interactions • van der Waals forces: stickiness – ~0. 1 kcal/mol per contact – induced polarization, London dispersion forces – typically modeled with 12 -6 Lennard. Jones potential – 1/r 6 attractive, 1/r 12 repulsive – minimum at around sum of VDW radii

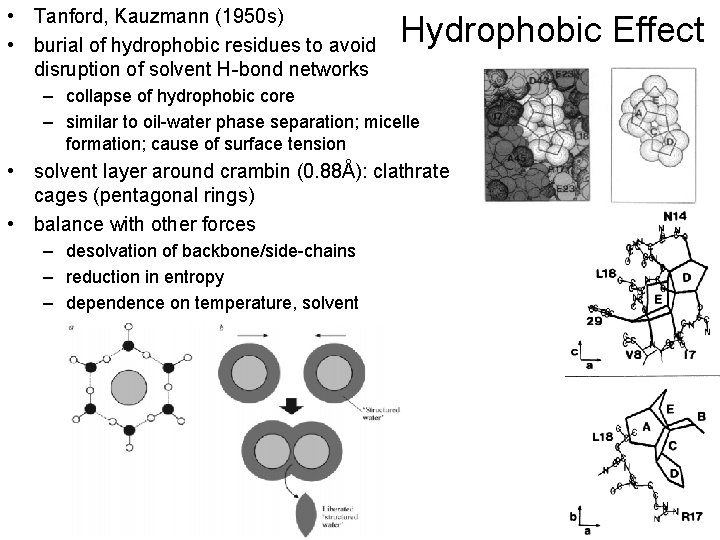
• Tanford, Kauzmann (1950 s) • burial of hydrophobic residues to avoid disruption of solvent H-bond networks Hydrophobic Effect – collapse of hydrophobic core – similar to oil-water phase separation; micelle formation; cause of surface tension • solvent layer around crambin (0. 88Å): clathrate cages (pentagonal rings) • balance with other forces – desolvation of backbone/side-chains – reduction in entropy – dependence on temperature, solvent