Forces for extensions of meanfield Extensions of meanfield

  • Slides: 16
Download presentation
Forces for extensions of meanfield § Extensions of mean-field ? § Why a new

Forces for extensions of meanfield § Extensions of mean-field ? § Why a new force ? and which forces ? § Some results § Perspectives Ph. D Thesis Marlène Assié Denis Lacroix (LPC Caen), Jean-Antoine Scarpaci (IPN Orsay)

Beyond the mean-field E/A=5 Me. V/u E/A=150 Me. V/u LOW ENERGY INTERMEDIATE ENERGY Extended

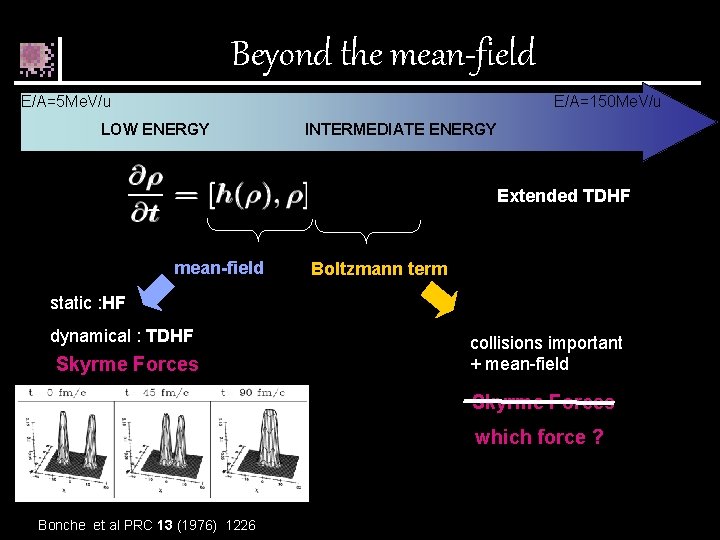
Beyond the mean-field E/A=5 Me. V/u E/A=150 Me. V/u LOW ENERGY INTERMEDIATE ENERGY Extended TDHF mean-field Boltzmann term static : HF dynamical : TDHF Skyrme Forces collisions important + mean-field Skyrme Forces which force ? Bonche et al PRC 13 (1976) 1226

Zero range force versus finite range force • Time Dependent Density Matrix : •

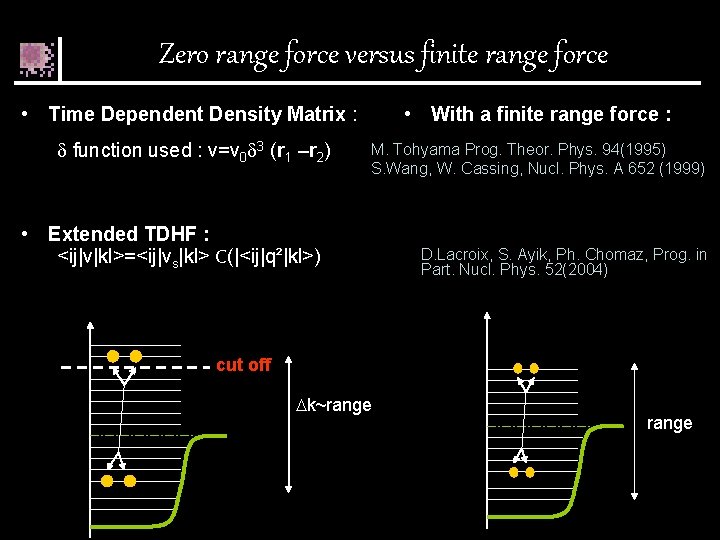
Zero range force versus finite range force • Time Dependent Density Matrix : • With a finite range force : function used : v=v 0 3 (r 1 –r 2) M. Tohyama Prog. Theor. Phys. 94(1995) S. Wang, W. Cassing, Nucl. Phys. A 652 (1999) • Extended TDHF : <ij|v|kl>=<ij|vs|kl> C(|<ij|q²|kl>) D. Lacroix, S. Ayik, Ph. Chomaz, Prog. in Part. Nucl. Phys. 52(2004) cut off k~range

The collision term • In the semi-classical limit p 1 p 3 k k’

The collision term • In the semi-classical limit p 1 p 3 k k’ p 2 loss p 4 gain interaction dependence Forces in the collision term might be fitted to the nucleon cross-section

Total Cross Section (mb) Cross Section for various Skyrme forces and the Gogny force

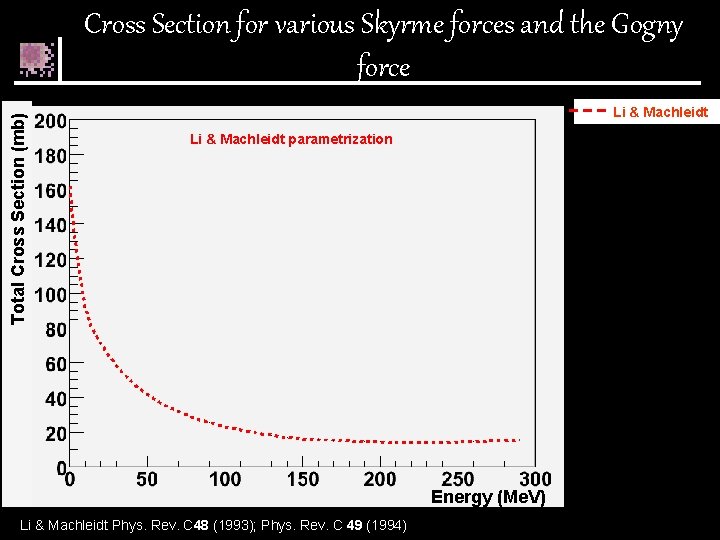
Total Cross Section (mb) Cross Section for various Skyrme forces and the Gogny force Li & Machleidt parametrization Energy (Me. V) Li & Machleidt Phys. Rev. C 48 (1993); Phys. Rev. C 49 (1994)

Cross Section for various Skyrme forces and the Gogny force Total Cross Section (mb)

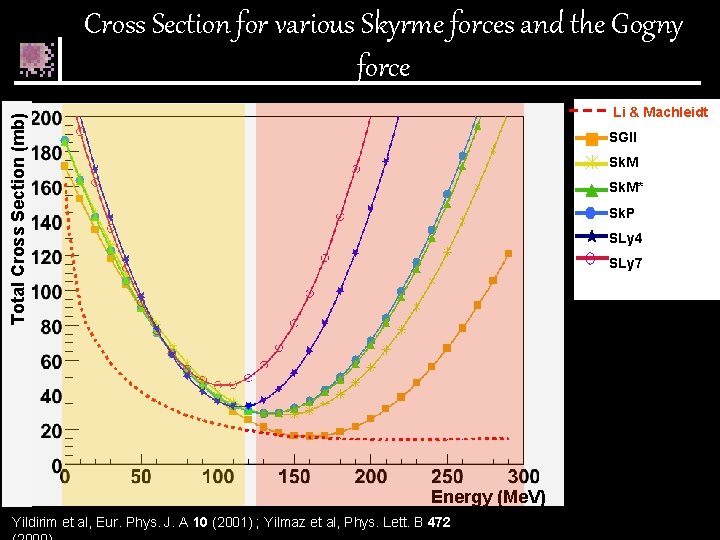
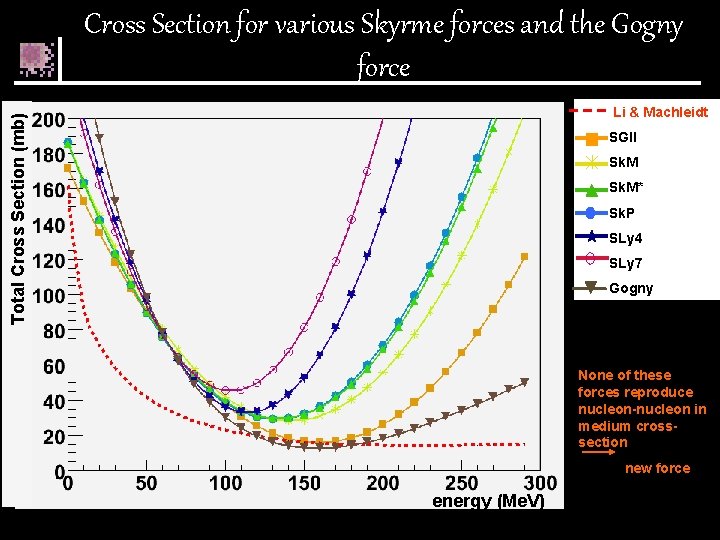
Cross Section for various Skyrme forces and the Gogny force Total Cross Section (mb) Li & Machleidt SGII Sk. M* Sk. P SLy 4 SLy 7 Energy (Me. V) Yildirim et al, Eur. Phys. J. A 10 (2001) ; Yilmaz et al, Phys. Lett. B 472

Cross Section for various Skyrme forces and the Gogny force Total Cross Section (mb)

Cross Section for various Skyrme forces and the Gogny force Total Cross Section (mb) Li & Machleidt SGII Sk. M* Sk. P SLy 4 SLy 7 Gogny None of these forces reproduce nucleon-nucleon in medium crosssection new force energy (Me. V)

Fitted force • Force of finite-range and separable § Gaussian (G) Ä finite-range §

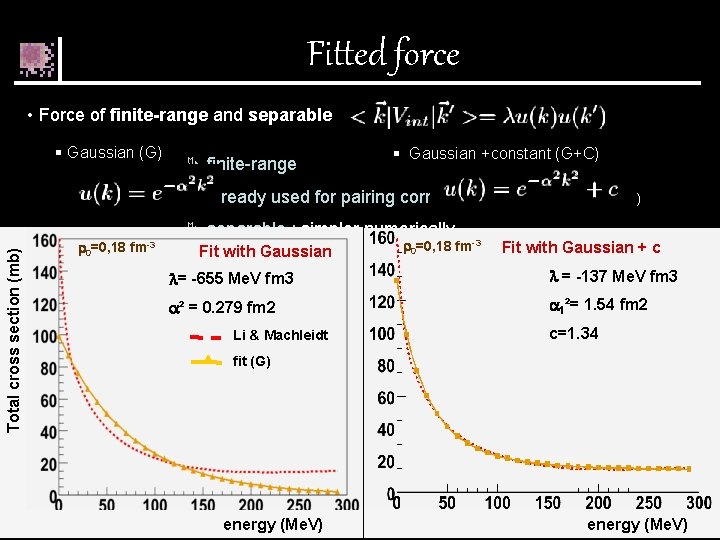
Fitted force • Force of finite-range and separable § Gaussian (G) Ä finite-range § Gaussian +constant (G+C) Total cross section (mb) Ä already used for pairing correlations Duguet PRC 69 (2004) 0=0, 18 fm-3 Ä separable : simpler numerically Fit with Gaussian 0=0, 18 fm-3 Fit with Gaussian + c = -655 Me. V fm 3 = -137 Me. V fm 3 ² = 0. 279 fm 2 1²= 1. 54 fm 2 Li & Machleidt c=1. 34 fit (G) energy (Me. V)

Density dependence Parameterization of Li & Machleidt E=50 Me. V Total cross section (mb)

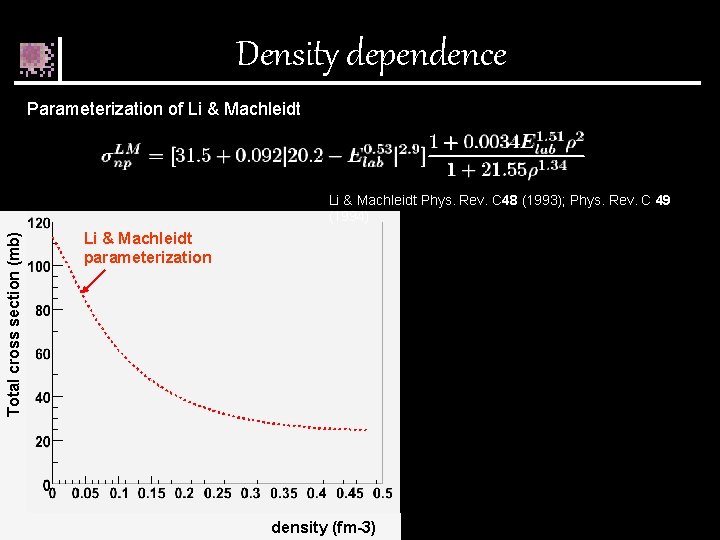
Density dependence Parameterization of Li & Machleidt E=50 Me. V Total cross section (mb) Li & Machleidt Phys. Rev. C 48 (1993); Phys. Rev. C 49 (1994) Li & Machleidt parameterization density (fm-3)

Density dependence Parameterization of Li & Machleidt E=50 Me. V Total cross section (mb)

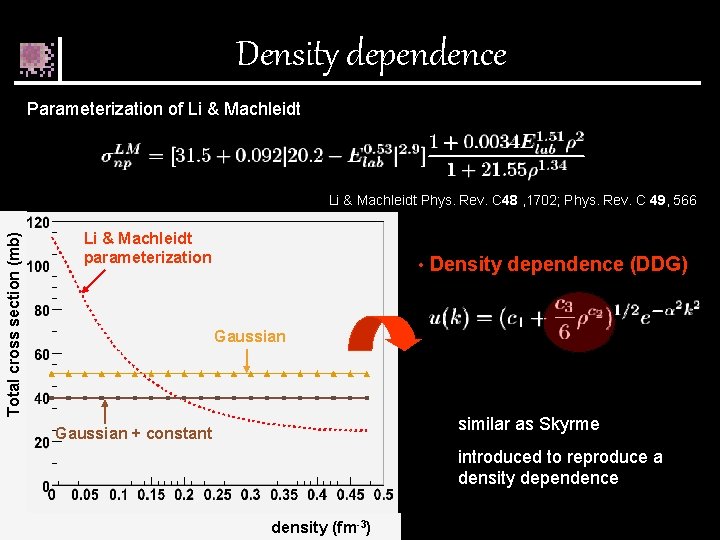
Density dependence Parameterization of Li & Machleidt E=50 Me. V Total cross section (mb) Li & Machleidt Phys. Rev. C 48 , 1702; Phys. Rev. C 49, 566 Li & Machleidt parameterization • Density dependence (DDG) Gaussian similar as Skyrme Gaussian + constant introduced to reproduce a density dependence density (fm-3)

Fit with the density dependent function • Fit method : 2 dimensions fit on

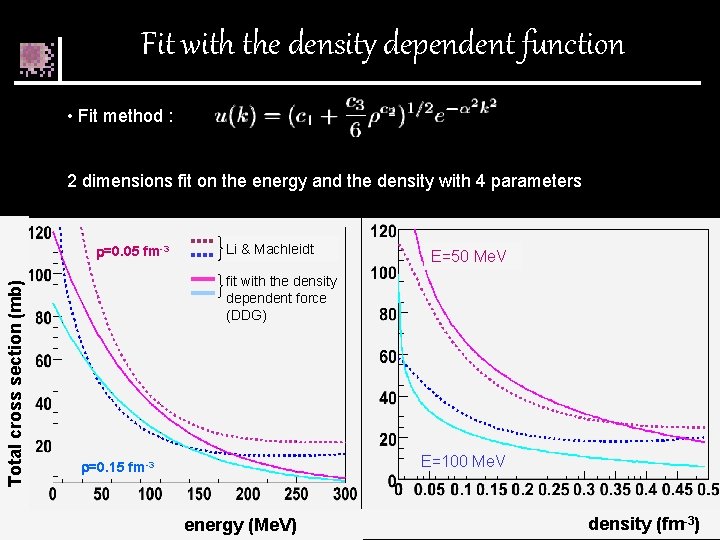
Fit with the density dependent function • Fit method : 2 dimensions fit on the energy and the density with 4 parameters Total cross section (mb) =0. 05 fm-3 Li & Machleidt E=50 Me. V fit with the density dependent force (DDG) E=100 Me. V =0. 15 fm-3 energy (Me. V) density (fm-3)

Fit with a sum of Gaussian and density dependence • Fit method : Total

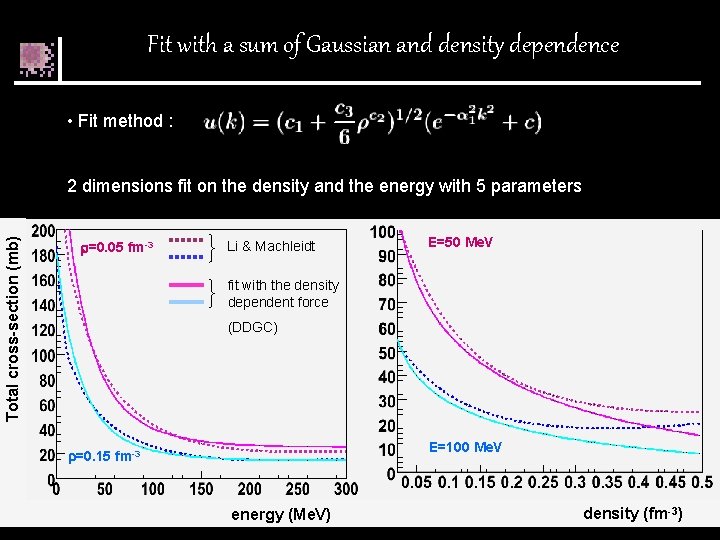
Fit with a sum of Gaussian and density dependence • Fit method : Total cross-section (mb) 2 dimensions fit on the density and the energy with 5 parameters =0. 05 fm-3 Li & Machleidt E=50 Me. V fit with the density dependent force (DDGC) E=100 Me. V =0. 15 fm-3 energy (Me. V) density (fm-3)

Summary • 2 forces which reproduce density and energy dependence of the nucleon-nucleon cross

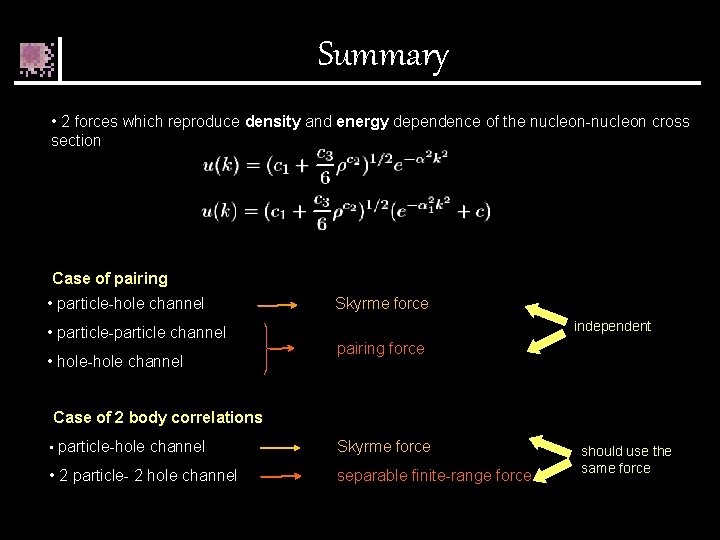
Summary • 2 forces which reproduce density and energy dependence of the nucleon-nucleon cross section Case of pairing • particle-hole channel • particle-particle channel • hole-hole channel Skyrme force independent pairing force Case of 2 body correlations • particle-hole channel Skyrme force • 2 particle- 2 hole channel separable finite-range force should use the same force

Comparison with the Skyrme force when k 0 and =0 • Skyrme Force t

Comparison with the Skyrme force when k 0 and =0 • Skyrme Force t 0 • Gaussian t 1 -2 ² • Gaussian density dependent t 0 t 1 -2 ² t 3 c 3 Skyrme forces Gaussian (G) Gaussian+ constant (GC) Gaussian density dependent Gaussian+ constant density dependent Up to 10 parameters 2 parameters 3 parameters 4 parameters 5 parameters t 0=-2931 to -1057 Me. V. fm 3 - 655 Me. V. fm 3 - 748 Me. V. fm 3 - 2416 Me. V. fm 3 -2572 Me. V. fm 3 t 1=235 to 970 Me. V. fm 5 183 Me. V. fm 5 491 Me. V. fm 5 1038 Me. V. fm 5 1896 Me. V. fm 5 t 2=-556 to 107 Me. V. fm 5 Neglected t 3=8000 to 18708 Me. V. fm(3+3 ) 13107 Me. V. fm 3+3 13891 Me. V. fm 3+3 =1/6 to 1 0. 17

t 0=-2645 Me. V. fm 3 t 0= -2416 Me. V. fm 3 t

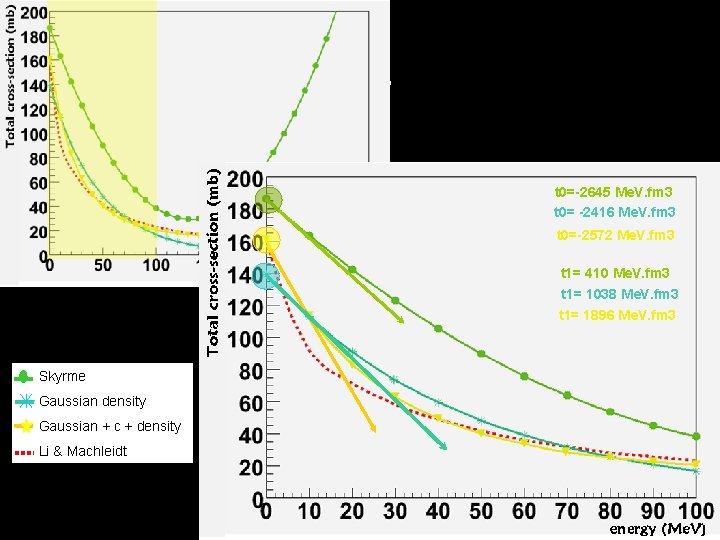
t 0=-2645 Me. V. fm 3 t 0= -2416 Me. V. fm 3 t 0=-2572 Me. V. fm 3 t 1= 410 Me. V. fm 3 t 1= 1038 Me. V. fm 3 t 1= 1896 Me. V. fm 3 Skyrme Gaussian density Gaussian + c + density Li & Machleidt

Perspectives • Time Dependent Density Matrix (TDDM) W. Cassing, S. J. Wang, Z. Phys.

Perspectives • Time Dependent Density Matrix (TDDM) W. Cassing, S. J. Wang, Z. Phys. A, 328 (1987) § truncation of the BBGKY hierarchy § takes into account all the two body correlations (extension of HF) Skyrme force separable finite- range force • Perspectives : study of correlations between two neutrons in borromean nuclei Experiment planned for July 2006 at GANIL

Forces 6 Forces 5 Forces 4 Forces 3Forces 6 Forces 5 Forces 4 Forces 3
Intramolecular Forces vs Intermolecular Forces Intramolecular Forces forcesIntramolecular Forces vs Intermolecular Forces Intramolecular Forces forces
Bots et extensions Que sont les extensions ExtensionsBots et extensions Que sont les extensions Extensions
Extensions of meanfield with stochastic methods Denis LacroixExtensions of meanfield with stochastic methods Denis Lacroix
Forces Motion Forces n Forces are acting allForces Motion Forces n Forces are acting all
Forces Forces There are many different forces whichForces Forces There are many different forces which
Forces Forces There are many different forces whichForces Forces There are many different forces which
Intermolecular Forces 11 2 Intermolecular Forces The forcesIntermolecular Forces 11 2 Intermolecular Forces The forces
Intramolecular and Intermolecular Forces Intramolecular Forces The forcesIntramolecular and Intermolecular Forces Intramolecular Forces The forces
Intermolecular Forces Intermolecular forces are attractive forces betweenIntermolecular Forces Intermolecular forces are attractive forces between
Intermolecular Forces Intermolecular forces are attractive forces betweenIntermolecular Forces Intermolecular forces are attractive forces between
Forces and FreeBody Diagrams Forces Review Common ForcesForces and FreeBody Diagrams Forces Review Common Forces
Intermolecular Forces Intermolecular forces are attractive forces betweenIntermolecular Forces Intermolecular forces are attractive forces between
Types of Forces Contact Forces Forces at aTypes of Forces Contact Forces Forces at a
Internal vs External Forces Internal Forces External ForcesInternal vs External Forces Internal Forces External Forces