Force Systems Combination Systems connected masses Horizontal Pulley

Force Systems • Combination Systems – connected masses • Horizontal Pulley • Atwood’s Machine

For any force system you must sum forces. Fnet = SF = F 1 + F 2 … ma = F 1 + F 2 …

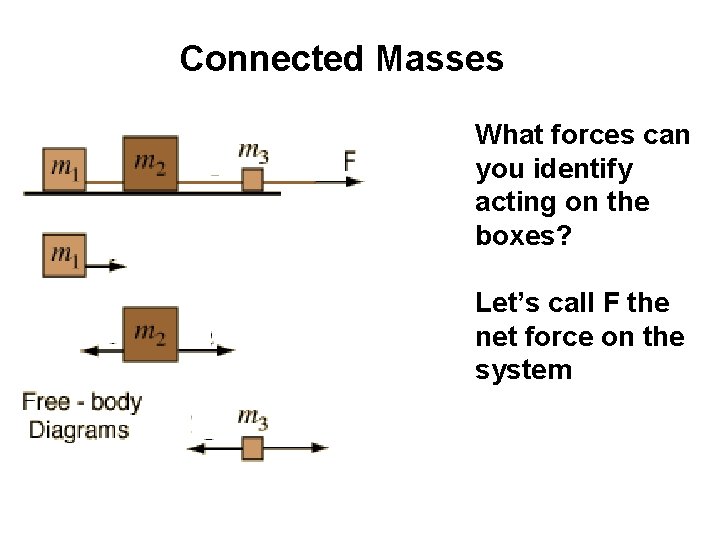
Connected Masses What forces can you identify acting on the boxes? Let’s call F the net force on the system

Fnet must accelerate the entire system’s mass together. Fnet = mtota

Given the masses and Fnet: sketch free body diagrams for each mass ignore vertical forces. Assign 1 direction as positive (right). Write the Fnet equation for each, find acceleration. then isolate each masses to find T 1 & T 2. m 1 a = T 1. m 2 a = T 2 - T 1. m 3 a = F – T 2.

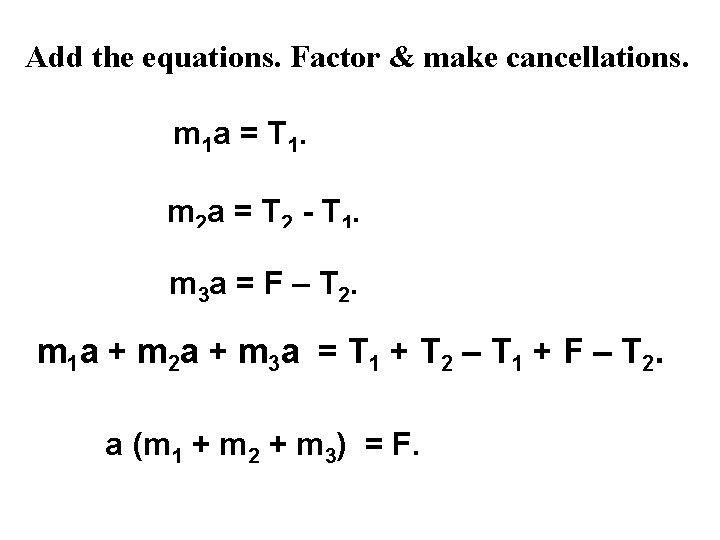
Add the equations. Factor & make cancellations. m 1 a = T 1. m 2 a = T 2 - T 1. m 3 a = F – T 2. m 1 a + m 2 a + m 3 a = T 1 + T 2 – T 1 + F – T 2. a (m 1 + m 2 + m 3) = F.

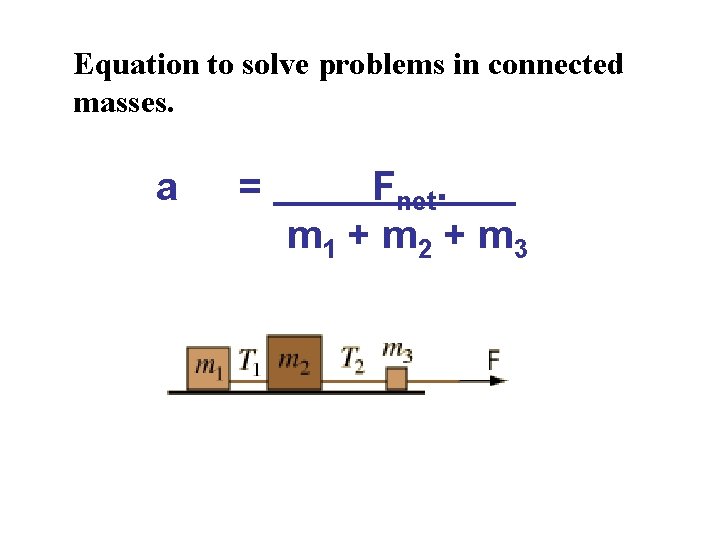
Equation to solve problems in connected masses. a = Fnet. m 1 + m 2 + m 3

Ex 1: Connected Masses: Given a Fnet of 20 N and masses of 4, 3, and 1 kg, find the acceleration of the system and the tension in each cord. 20 N (4 + 3 + 1) kg a = 2. 5 m/s 2.

Use the free body diagram & known acceleration to find the tension in each cord. 4 kg m 1 a = T 1 = (4 kg)(2. 5 m/s 2) = 10 N. m 3 a = F -T 2 Fnet - m 3 a = T 2. 20 N - (1 kg)(2. 5 m/s 2) = 1 kg 17. 5 N

Check the calculation using the 3 rd mass. T 2 – T 1 = m 2 a 17. 5 N – 10 N = 7. 5 N m 2 a = (3 kg)(2. 5 m/s 2) = 7. 5 N. It is correct!!

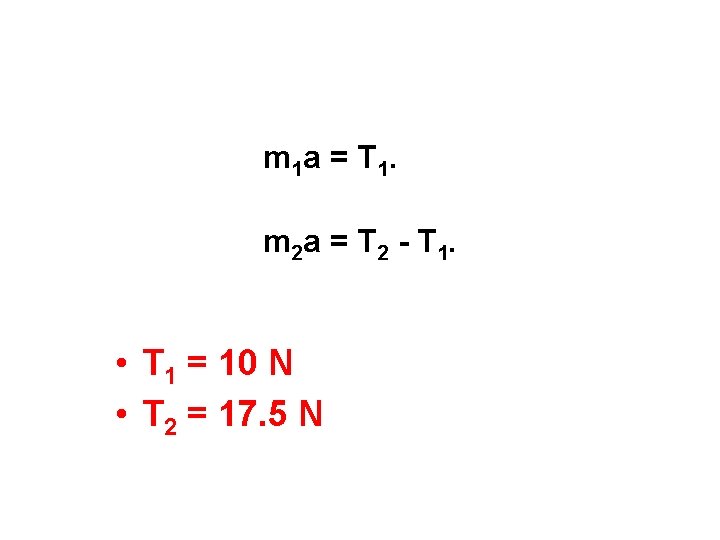
m 1 a = T 1. m 2 a = T 2 - T 1. • T 1 = 10 N • T 2 = 17. 5 N

Horizontal Pulley.

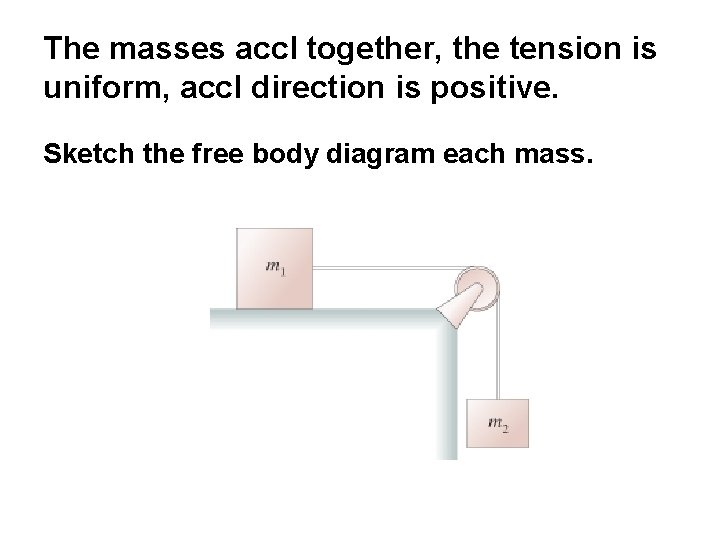
The masses accl together, the tension is uniform, accl direction is positive. Sketch the free body diagram each mass.

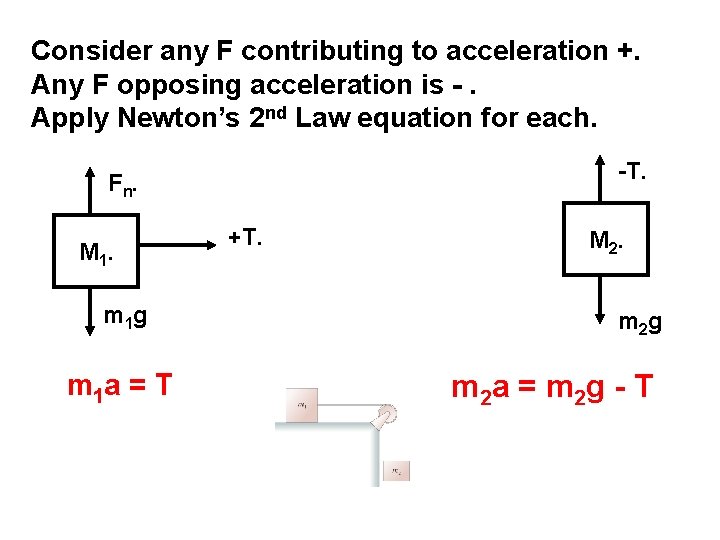
Consider any F contributing to acceleration +. Any F opposing acceleration is -. Apply Newton’s 2 nd Law equation for each. -T. F n. M 1. m 1 g m 1 a = T +T. M 2. m 2 g m 2 a = m 2 g - T

Add the equations: m 1 a + m 2 a = T + m 2 g – T T cancels. m 1 a + m 2 a = m 2 g Factor a & solve

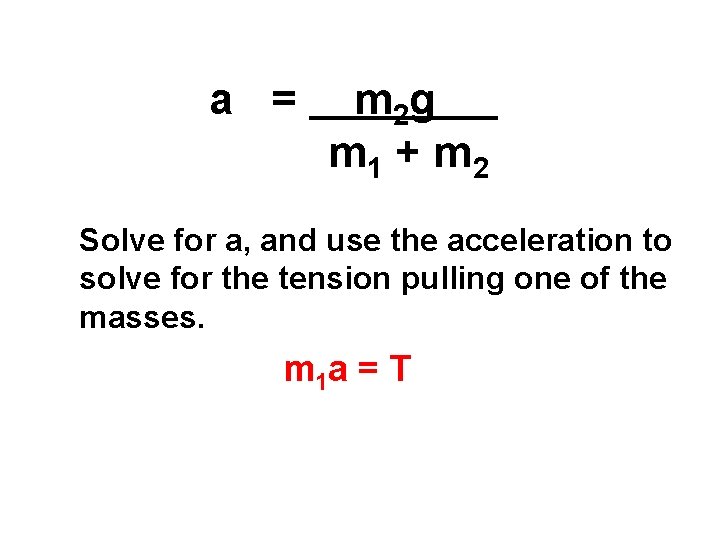
a = m 2 g m 1 + m 2 Solve for a, and use the acceleration to solve for the tension pulling one of the masses. m 1 a = T

Ex 2: Horizontal Pulley: Given a mass of 4 kg on a horizontal frictionless surface attached to a mass of 3 kg hanging vertically, calculate the acceleration, and the tension in the cord. Compare the tension to the weight of the hanging mass, are they the same?

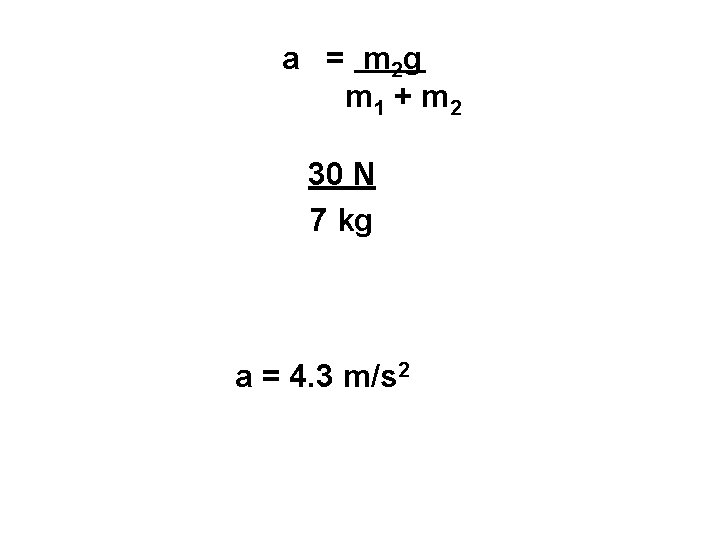
a = m 2 g m 1 + m 2 30 N 7 kg a = 4. 3 m/s 2

m 1 a = T • (4 kg)(4. 3 m/s 2) • T = 17 N • mg = 30 N, tension less than weight.

Atwood’s Machine Use wksht.

Sketch the free body

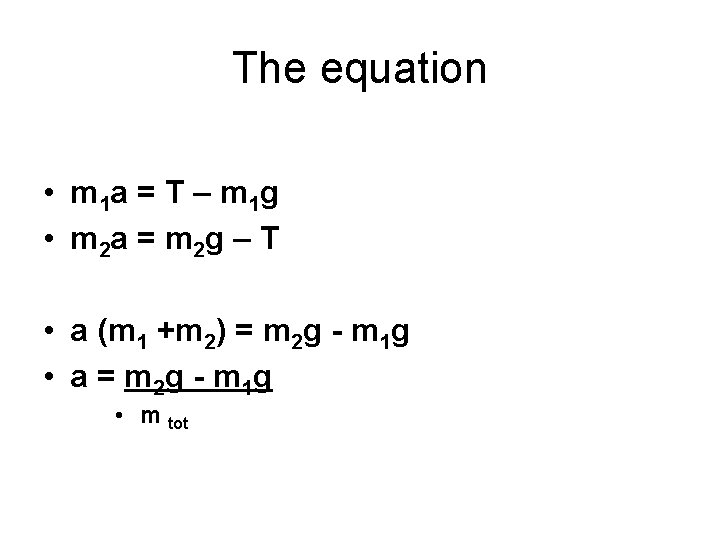
The equation • m 1 a = T – m 1 g • m 2 a = m 2 g – T • a (m 1 +m 2) = m 2 g - m 1 g • a = m 2 g - m 1 g • m tot

Given Atwood’s machine, m 1 = 2 kg, m 2 = 4 kg. Find the acceleration and tension. • a = 3. 3 m/s 2. • T = 26 N

Sketch the free body diagram for each.

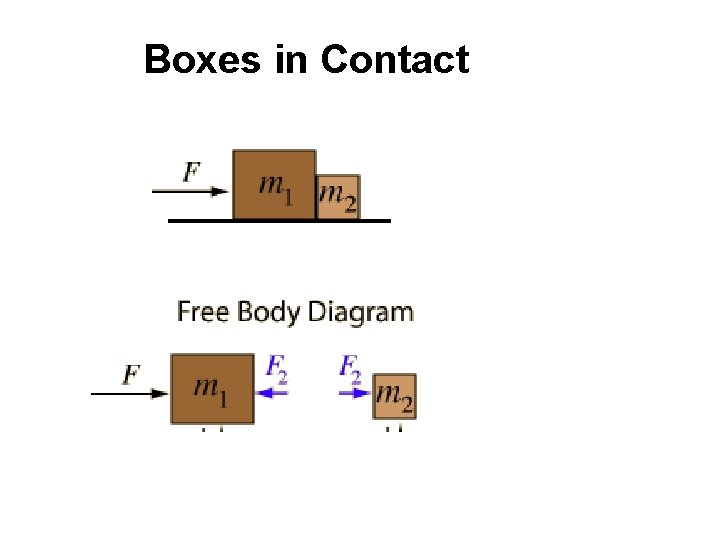
Boxes in Contact

Since F is the only force acting on the two masses, it determines the acceleration of both: The force F 2 acting on the smaller mass may now be determined.

Using the previously determined accl, the force F 2 acting on the smaller mass is F 2 = m 2 a

By Newton’s 3 rd Law, F 2 acts backward on m 1. The force on m 1 is: The net force, F 1, on m 1 is: F m 1 F 2

Given a force of 10 N applied to 2 masses, m 1 =5 kg and m 2 =3 kg, find the accl and find F 2 (the contact force) between the boxes. a = 1. 25 m/s 2 F 2 = 3. 75 N

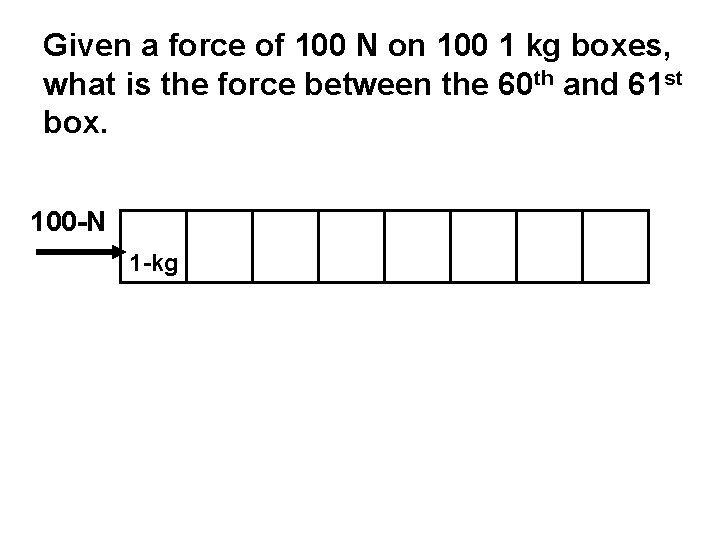
Given a force of 100 N on 100 1 kg boxes, what is the force between the 60 th and 61 st box. 100 -N 1 -kg

Find a for system. F 2 must push the remaining 40 boxes or 40 kg. 40 N.

Ignoring friction, derive an equation to solve for a and T for this system: Begin by sketching the free body diagram Write the equations for each box Add them. Solve for accl

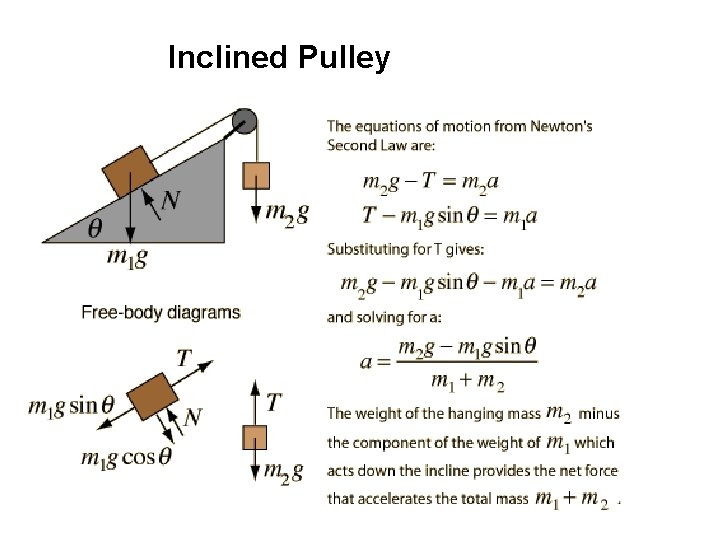
Inclined Pulley

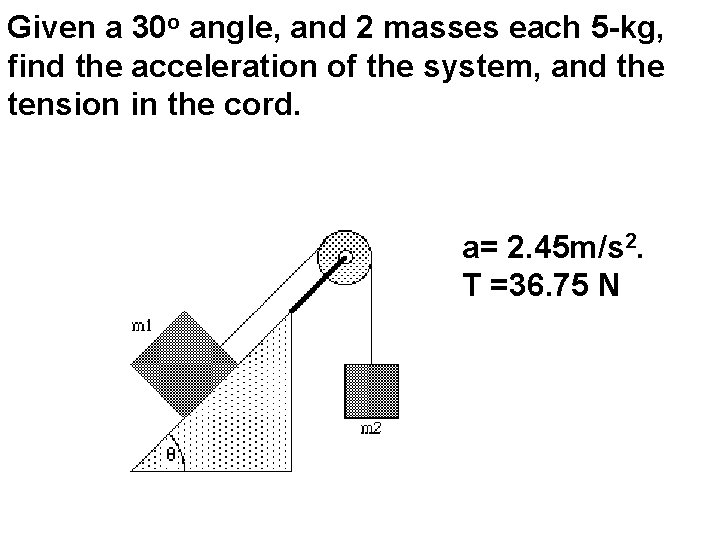
Given a 30 o angle, and 2 masses each 5 -kg, find the acceleration of the system, and the tension in the cord. a= 2. 45 m/s 2. T =36. 75 N

1. Derive an equation for the same inclined pulley system including friction between m 1 and the ramp.

Suppose m 1 = 5 kg, m 2 = 12 -kg and the ramp angle is 20 o. Find the m that would make the system acceleration 4 m/s 2. What will be the tension in the cord? • The m = 0. 7 • T = 69 N

To practice problems go to: Hyperphysics site. Click Mechanics, Newton’s Laws, Standard problems, then the appropriate symbol. • http: //hyperphysics. phyastr. gsu. edu/hbase/hph. html#mechcon