Folding Technique 1 Outline Special purpose hardware design

Folding Technique 1

Outline • • • Special purpose hardware design and DSP application demands and technologies Representations of DSP algorithms and architectures Compromising Folding technique Simple example – ad hoc folding Folding equation and mathematical background Preparation of source architecture for folding – problems Case study 1: Folded Bit-Serial Multiplier Case study 2: Configurable Folded FIR Filter Architecture 2

Special purpose hardware design and DSP • DSP systems can be realized using programmable processors or custom designed hardware circuits fabricated using very-large-scale-integrated (VLSI) circuit technology • Two import features that distinguish DSP from other general purpose computations are real-time throughput requirement and data driven property. 3

4

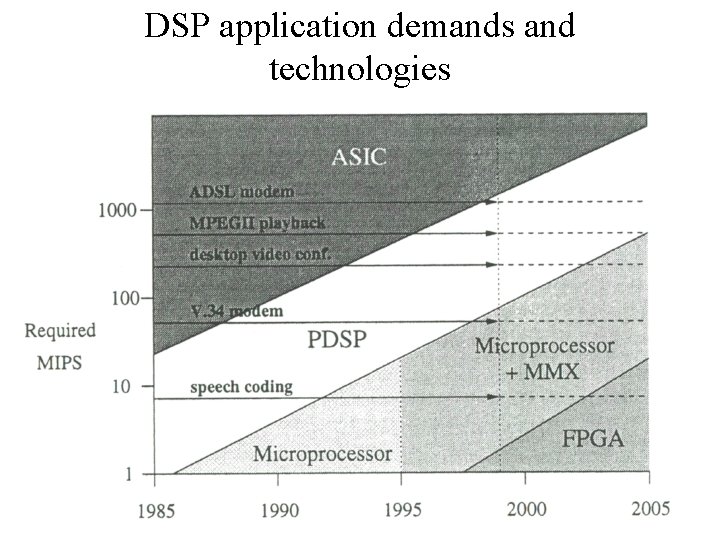
DSP application demands and technologies 5

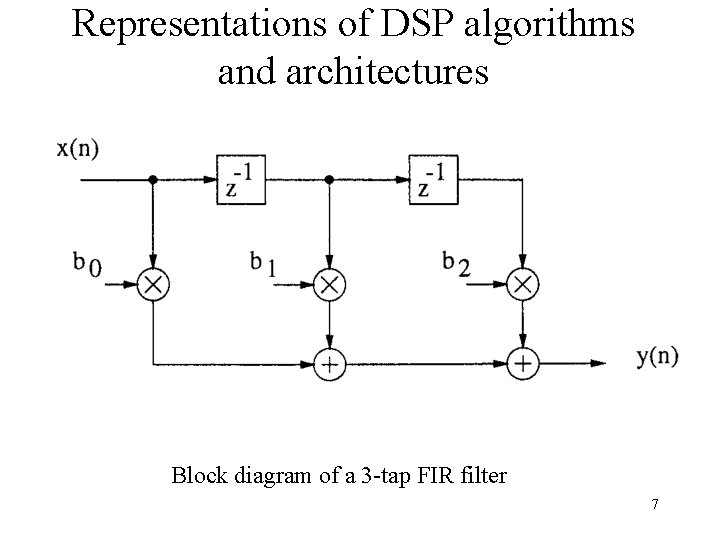
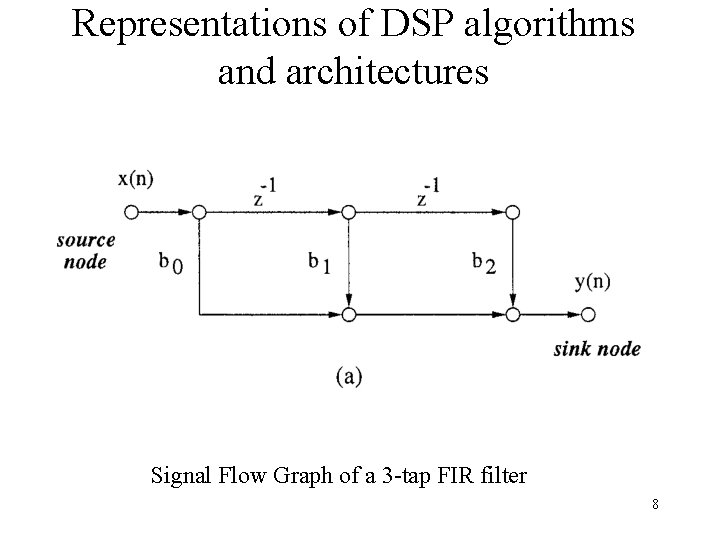
Representations of DSP algorithms and architectures DSP algorithms are initially described by mathematical formulas. System architecture can be described by Behavioral languages Applicative Graphical representations - BD - set of equations (not actions) - SFG Prescriptive - DFG - describe assigments Descriptive -VHDL, Verilog, . . . - DG 6

Representations of DSP algorithms and architectures Block diagram of a 3 -tap FIR filter 7

Representations of DSP algorithms and architectures Signal Flow Graph of a 3 -tap FIR filter 8

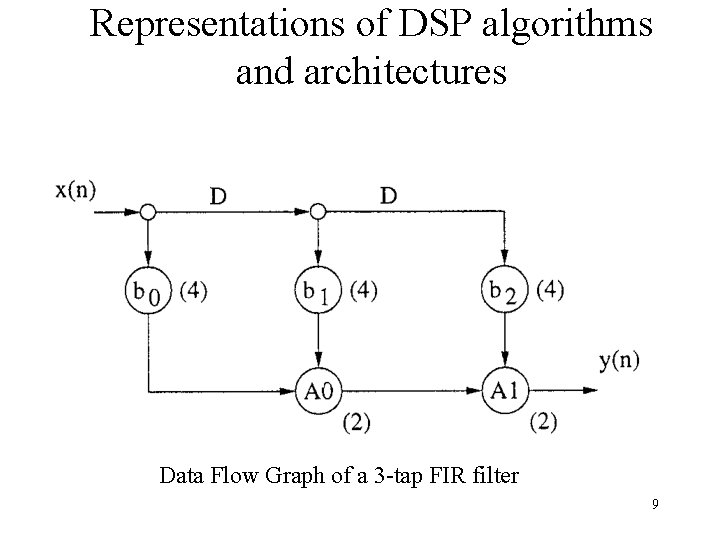
Representations of DSP algorithms and architectures Data Flow Graph of a 3 -tap FIR filter 9

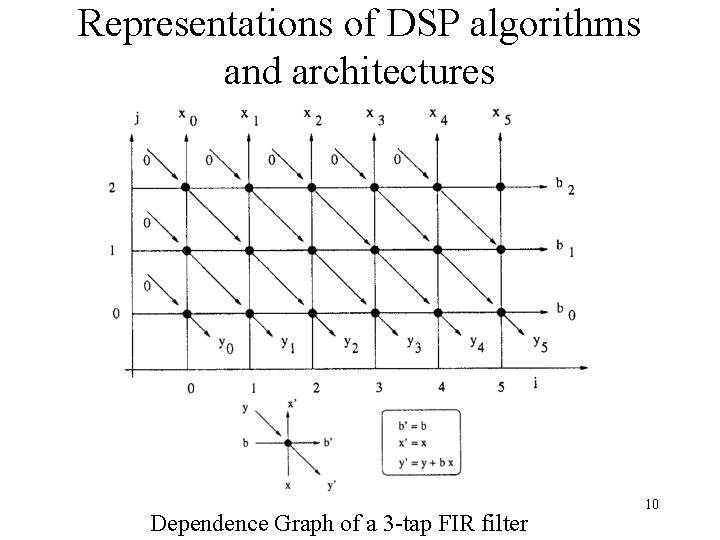
Representations of DSP algorithms and architectures Dependence Graph of a 3 -tap FIR filter 10

Compromising • Area – Time – Power • Area – Time • Goal: – to achieve time (throughput) requirements with optimal chip area or optimal using of chip resources 11

Folding technique • Performances and cost of any digital circuit depend on circuit design style. Therefore, creating a given architecture, to establish optimal area-time-power tradeoff, a careful choice of circuit design style to use is necessary. • In synthesizing DSP architectures, it is important to minimize the silicon area of the integrated circuits, which is achieved by reducing the number of functional units (such as multipliers and adders), registers, multiplexers, and interconnection wires. 12

Folding technique • How? • By executing multiple algorithm operations on a single functional unit, the number of functional units in the implementation is reduced, resulting in integrated circuit with low silicon area. 13

Simple example – ad hoc folding Two addition operations are folded to a single adder: Folding factor* N=2 *Folding factor - the number of algorithm operations folded to a single functional unit 14

Clk L. input Up. input Output 0 a(0) b(0) - 1 a(0)+b(0) c(0) - 2 a(1) b(1) a(0)+b(0)+c(0) 3 a(1)+b(1) c(1) - 4 a(2) b(2) a(1)+b(1)+c(1) 5 a(2)+b(2) c(2) - 15

Folding equation and math. background • K. K. Parhi, VLSI Digital Signal Processing Systems (Design and Implementation), John Wiley & Sons, In. , New York, 2000. • T. C. Denk, K. K. Parhi, Synthesis of Folded Pipelined Architectures for Multirate DSP Algorithms, IEEE Transaction on Very Large Scale Integration (VLSI) Systems, Vol. 6, No. 4, Dec. 1998, pp. 595 -607. The folding transformation provides a systematic technique for designing of control circuits in folded systems. 16

Folding equation and math. background An edge with w(e) delays The corresponding folded data path The data begin at the functional unit pipelining stages, pass through , which has delays, and are switched into the functional unit at the time instances , where N is the number of operations folded to a single functional unit (folding factor), while u and v are the folding orders of nodes U and V that satisfy 17.

Folding equation and math. background • A folding set, S, is defined as an ordered set of operations, which contains N entries, executed by the same functional unit. • For a folded system to be realizable must hold for all of the edges in the DFG. 18

Preparation of source architecture for folding – problems Important question: How to prepare the source architecture / DFG for the successful application of folding technique? 19

Preparation of source architecture for folding – problems • Once valid folding sets have been assigned, retiming can be used to satisfy this property or determine that the folding sets are not feasible. • Retiming is a transformation technique used to change the locations of delay elements without affecting the I/O characteristics of the circuit. • Retiming in synchronous circuit design can be directed towards: – Reducing the clock period, – Reducing the number of registers, – Reducing the power consumption, etc. 20

Preparation of source architecture for folding – problems • Using folding equations, a set of retiming inequalities can be obtained – Solution for architecture retiming can be found by mapping of set of inequalities onto constraint graph. – Algorithms: Bellman-Ford or Floyd-Warshall • Assigment of folding sets on functional units of retimed graph – Rechecking of folding condition 21

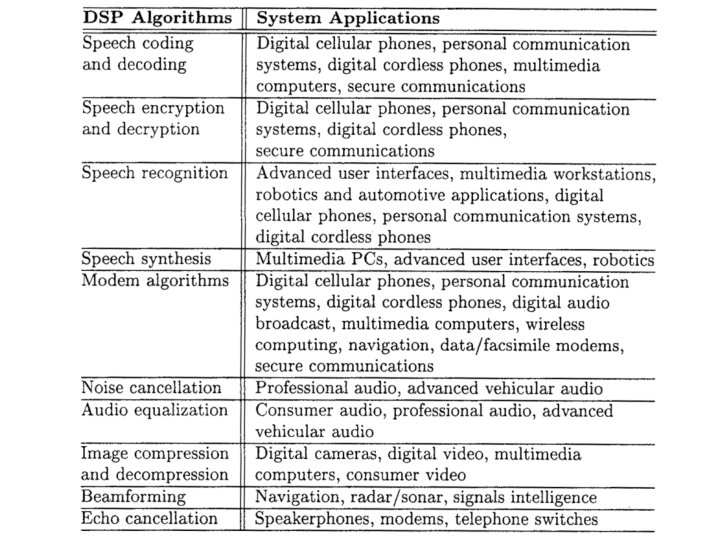
Case study 1: Folded Bit-Serial Multiplier • Public-key cryptography – special features are required for multiplier units. – RSA encryption and decryption, large integers (typically 1024 bits or more) must be multiplied, • Elliptic curve cryptosystems, – a multiplication in finite fields is required. 22

Case study 1: Folded Bit-Serial Multiplier Source architecture: basic serial-parallel-serial multiplier 23

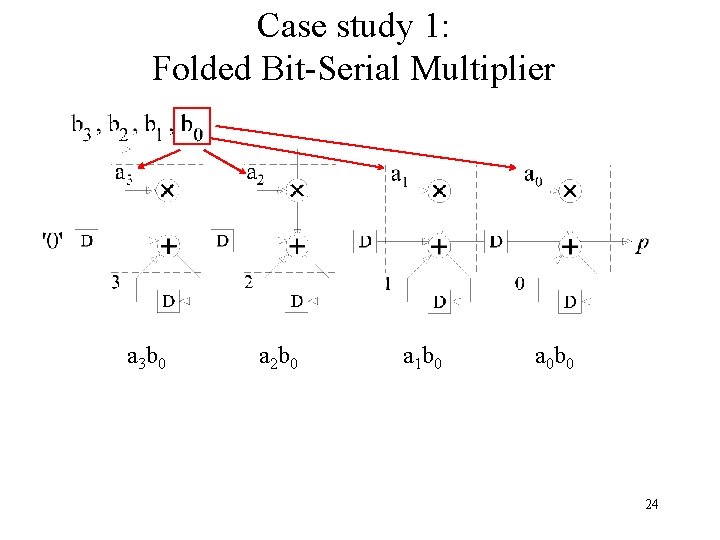
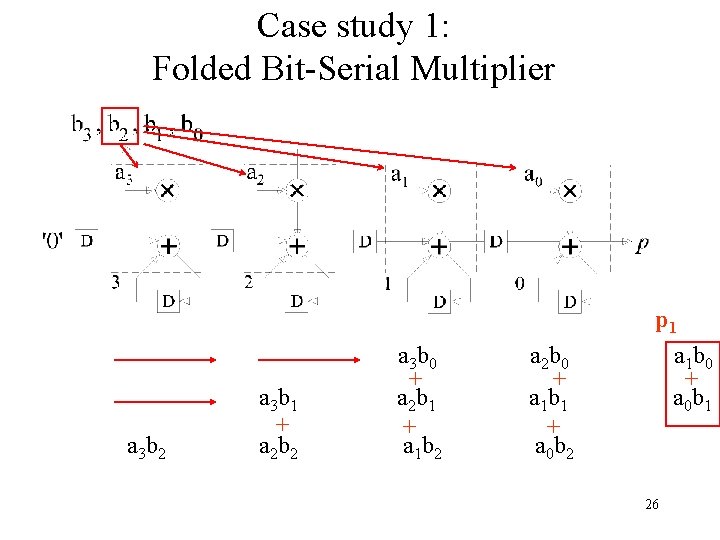
Case study 1: Folded Bit-Serial Multiplier a 3 b 0 a 2 b 0 a 1 b 0 a 0 b 0 24

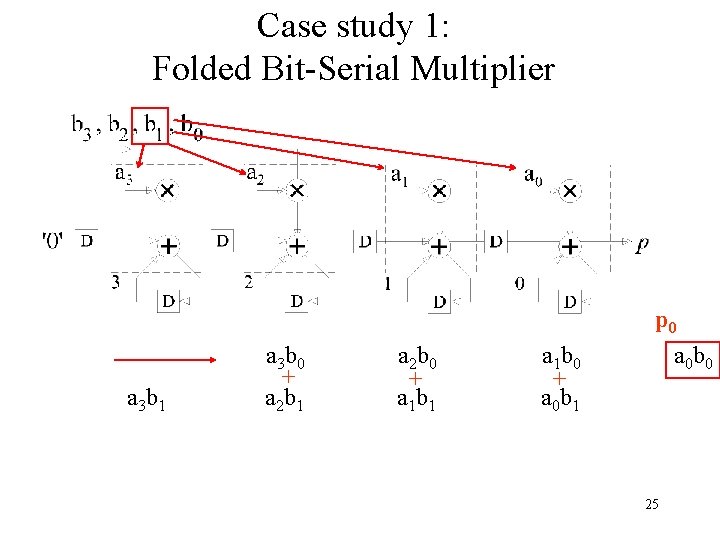
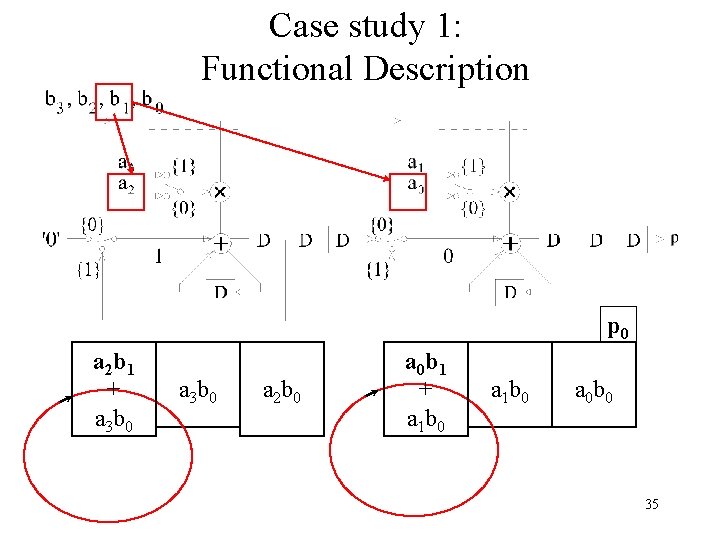
Case study 1: Folded Bit-Serial Multiplier a 3 b 1 a 3 b 0 + a 2 b 1 a 2 b 0 + a 1 b 1 a 1 b 0 + a 0 b 1 p 0 a 0 b 0 25

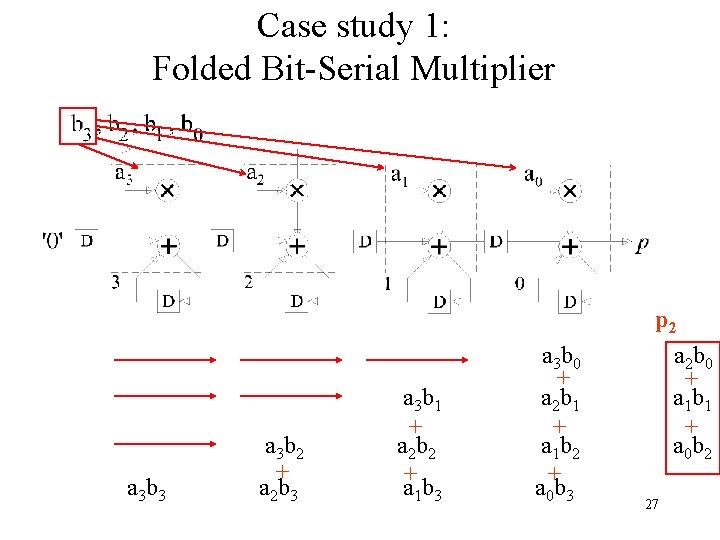
Case study 1: Folded Bit-Serial Multiplier a 3 b 2 a 3 b 1 + a 2 b 2 a 3 b 0 + a 2 b 1 + a 1 b 2 a 2 b 0 + a 1 b 1 + a 0 b 2 p 1 a 1 b 0 + a 0 b 1 26

Case study 1: Folded Bit-Serial Multiplier a 3 b 3 a 3 b 2 + a 2 b 3 a 3 b 1 + a 2 b 2 + a 1 b 3 a 3 b 0 + a 2 b 1 + a 1 b 2 + a 0 b 3 p 2 a 2 b 0 + a 1 b 1 + a 0 b 2 27

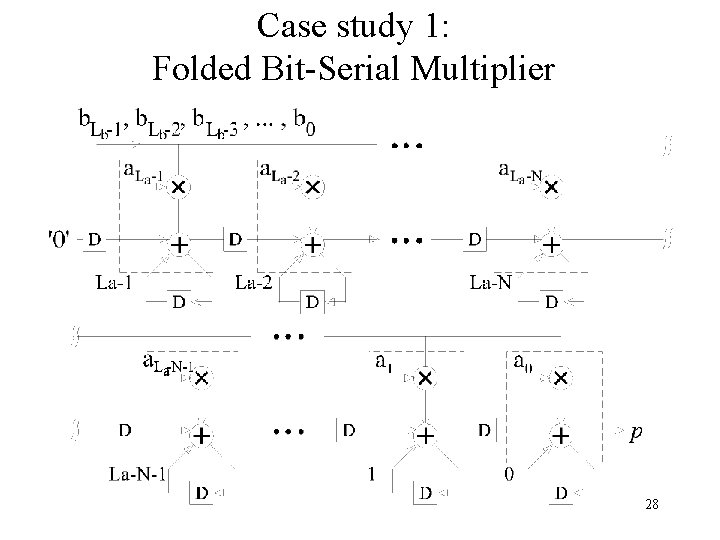
Case study 1: Folded Bit-Serial Multiplier 28

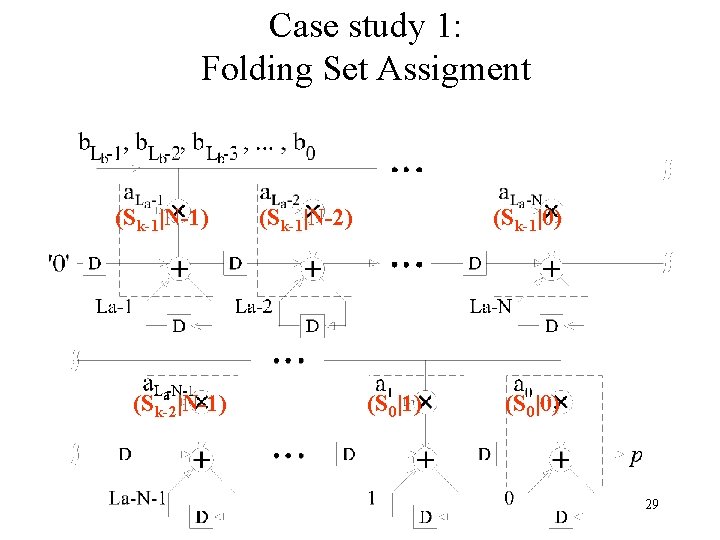
Case study 1: Folding Set Assigment (Sk-1|N-1) (Sk-2|N-1) (Sk-1|N-2) (Sk-1|0) (S 0|1) (S 0|0) 29

Case study 1: Folding Equations • Two neighboring nodes that are folded onto one node Df(i i+1)=N 1 -0+0 -1=N-1, i= N-1, 2 N-1, … , La-N-1 • Neighboring nodes that are folded onto different nodes Df(i i+1)=N 1 -0+(N-1)-0=2 N-1, i¹ N-1, 2 N-1, … , La-N-1 • Carry data paths Df(i i)=N 1 -0+0 -1=N-1, i= 0, 1, … , La-1 Df(U®V)³ 0 Folded architecture contains max(N-1, 2 N-1)=2 N-1 latches between nodes j and j+1 that will be used for data buffering 30

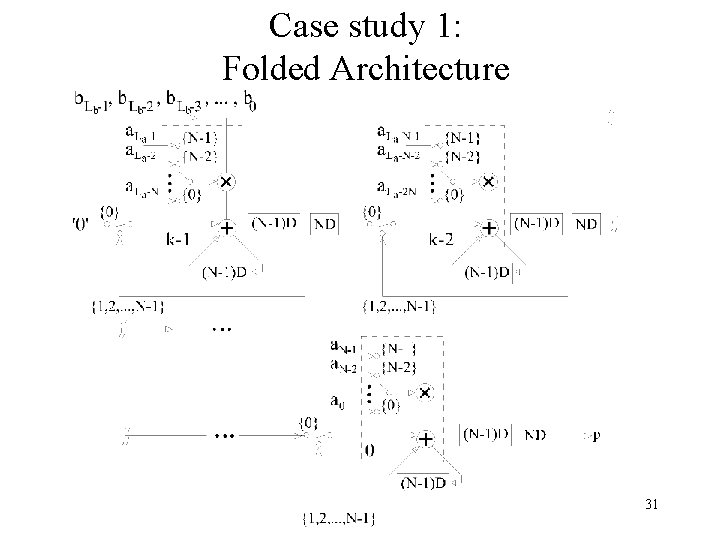
Case study 1: Folded Architecture 31

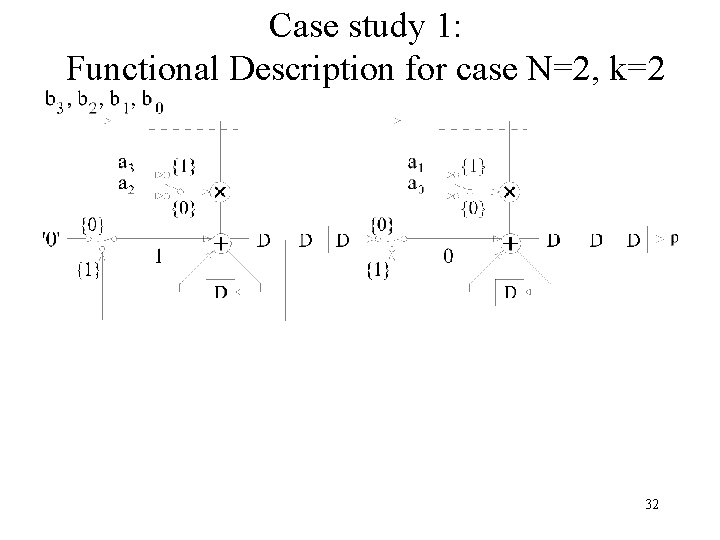
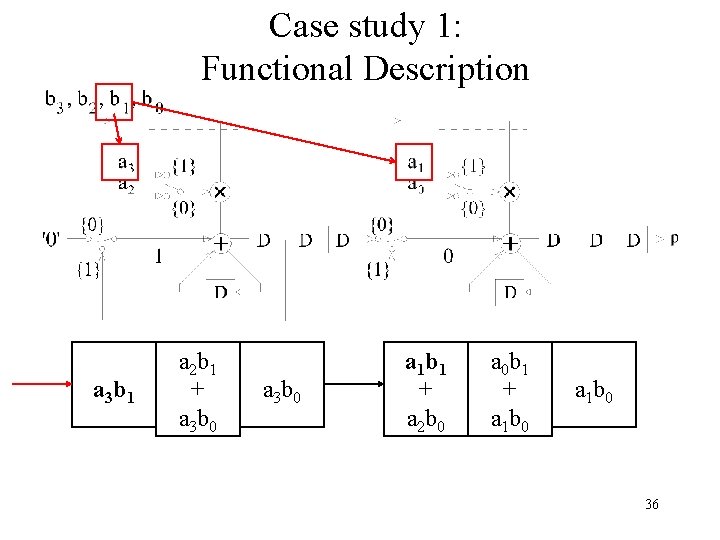
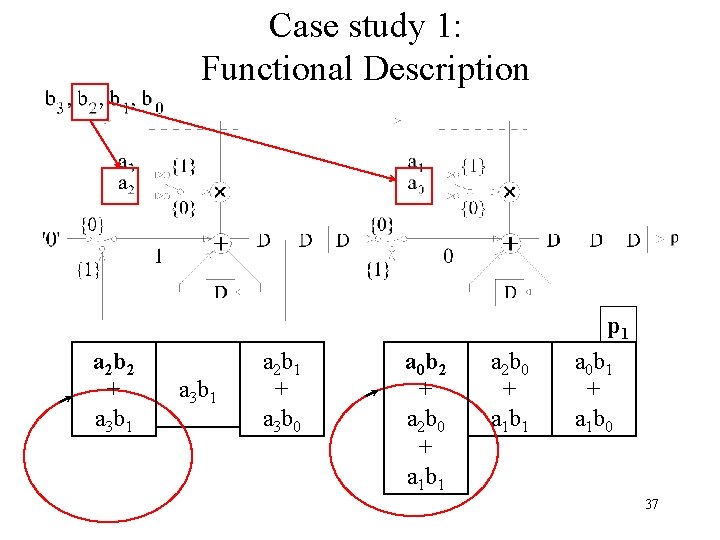
Case study 1: Functional Description for case N=2, k=2 32

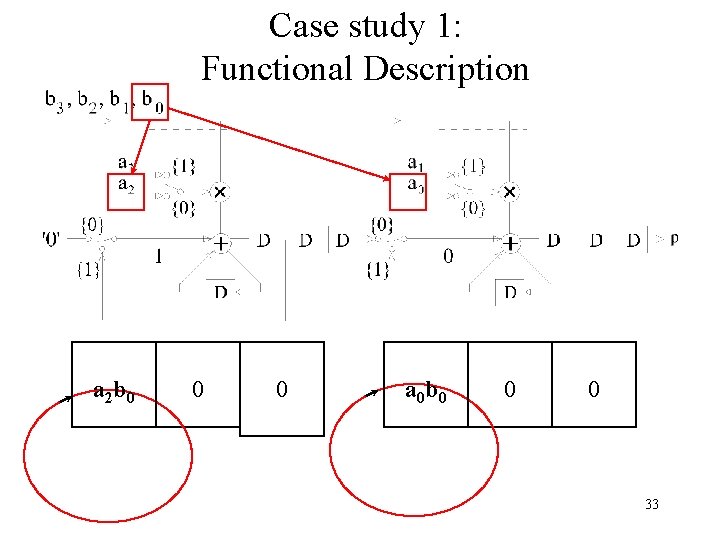
Case study 1: Functional Description a 2 b 0 0 0 a 0 b 0 0 0 33

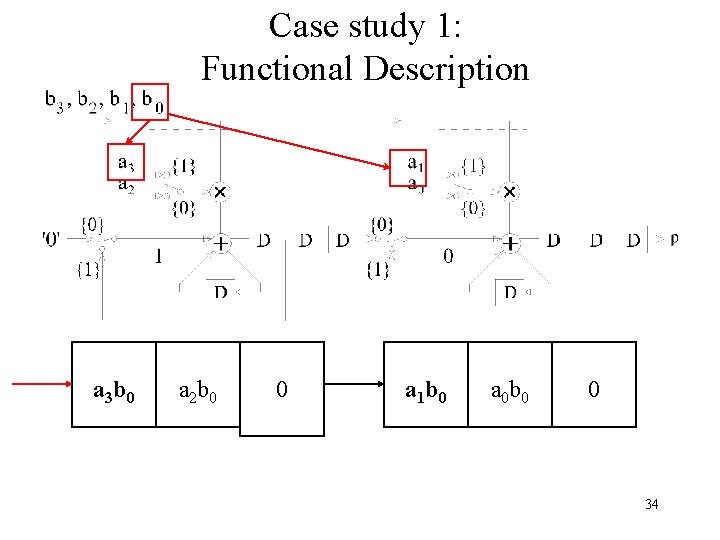
Case study 1: Functional Description a 3 b 0 a 2 b 0 0 a 1 b 0 a 0 b 0 0 34

Case study 1: Functional Description p 0 a 2 b 1 + a 3 b 0 a 2 b 0 a 0 b 1 + a 1 b 0 a 0 b 0 35

Case study 1: Functional Description a 3 b 1 a 2 b 1 + a 3 b 0 a 1 b 1 + a 2 b 0 a 0 b 1 + a 1 b 0 36

Case study 1: Functional Description p 1 a 2 b 2 + a 3 b 1 a 2 b 1 + a 3 b 0 a 0 b 2 + a 2 b 0 + a 1 b 1 a 0 b 1 + a 1 b 0 37

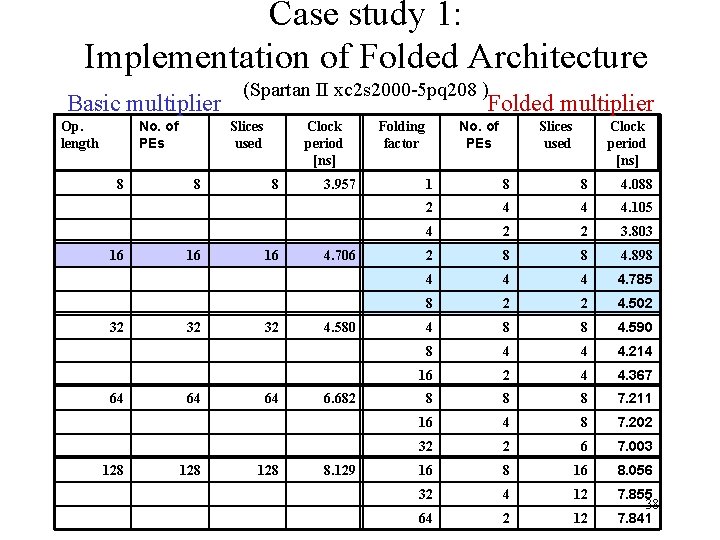
Case study 1: Implementation of Folded Architecture Basic multiplier No. of PEs Op. length 8 16 32 64 128 (Spartan II xc 2 s 2000 -5 pq 208 ) Folded multiplier Slices used 8 16 32 64 128 Clock period [ns] 8 16 32 64 128 3. 957 4. 706 4. 580 6. 682 8. 129 No. of PEs Folding factor Slices used Clock period [ns] 1 8 8 4. 088 2 4 4 4. 105 4 2 2 3. 803 2 8 8 4. 898 4 4. 785 8 2 2 4. 502 4 8 8 4. 590 8 4 4 4. 214 16 2 4 4. 367 8 8 8 7. 211 16 4 8 7. 202 32 2 6 7. 003 16 8. 056 32 4 12 64 2 12 7. 855 38 7. 841

Case study 1: Conclusions • It provides the finding of optimal area-time solution for the given requirements. • Saprtan II “shift register” property was used to relax the constraints caused by relatively large number of lathes in folded architecture. • Generated architecture has kept almost all desirable features of source Bit-Serial architecture. The hardware reduction of active arithmetic elements for the factor N is done at the cost of execution time. 39

Case study 2: • Cellular-phone technology is changing rapidly. There is an increasing number of wireless-communications standards, including variants of the IEEE 802. 11 wireless LAN specification, etc… – Traditionally, devices need a separate chip to work with each standard. • Providers differentiate themselves by offering new features, such as multimedia capabilities. – Providing each feature typically requires a separate chip, or essence, multiple circuitry systems physically joined on a peace of silicon 40

Case study 2: • The additional circuitry adds cost, takes up space, increases power usage in mobile devices, and increase product-design time. 41

Case study 2: Configurable Folded FIR Filter Architecture • The synthesis of configurable folded bitplane architecture for FIR filtering. • Why? Ø Wider application area Ø Finding of suitable A-T tradeoffs Ø Increasing of versatility of folded systems 42

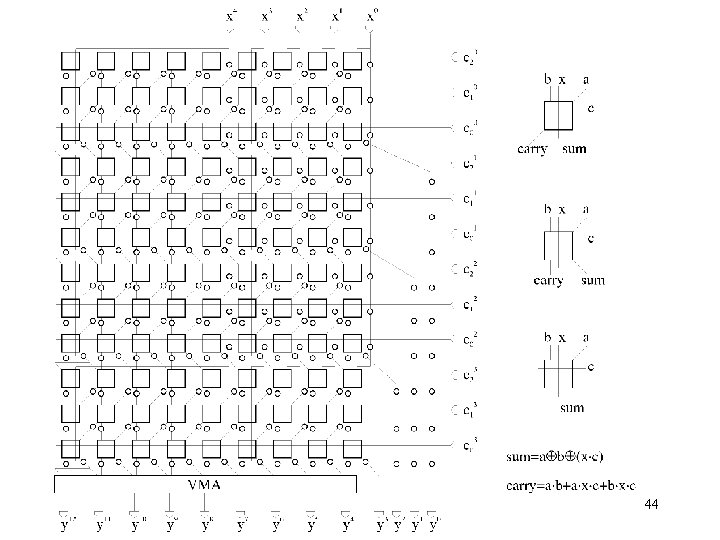
Case study 2: FIR filtering Output words {yi} of FIR filter are computed as where words. m k n are coefficients while {xi} are input – coefficient word length, – number of taps, – bit of coefficient (with weight ) – input word length. The BPA is obtained by resorting of partial products of different multipliers. 43

44

Case study 2: Bit-plane FIR filter architecture • • • highly regular architecture allows extensive pipelining regular layout high computational throughput truncation of LSBs of intermediate results without any loss of accuracy • programmability of coefficients [Noll 1986], [Reuver & Klar 1992] 45

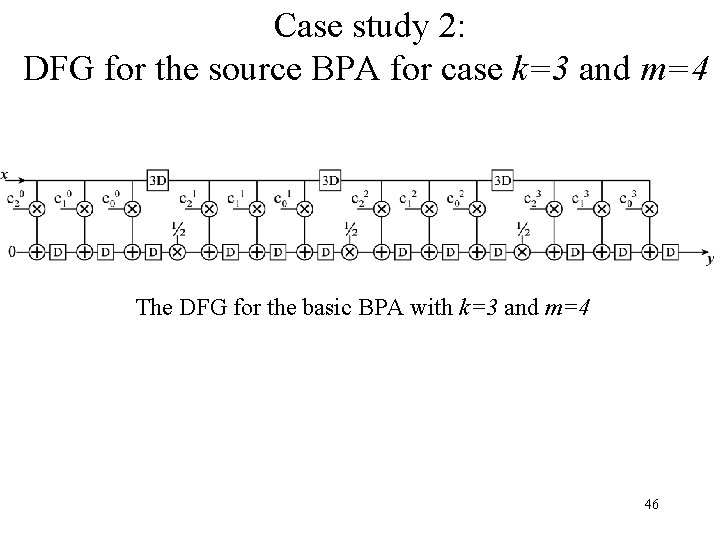
Case study 2: DFG for the source BPA for case k=3 and m=4 The DFG for the basic BPA with k=3 and m=4 46

Case study 2: Assignment of folding sets (Ss , r) s= p mod k r= p mod N 47

Case study 2: Assignment of folding sets • Folding set assignment enables the changing of operations in folding sets. • Different operations can be mapped onto the different hardware units in fixed array structure. • There are k folding sets where each folding set contains N operations. • For the coefficients, kc, and the coefficient length, mc, the total number of operations, L, is: L=kc mc=k N 48

Case study 2: Folding equations and retiming • General form of Folding Equations: Df (p p+1)=N w(e)-0+[(p+1) mod N]-[p mod N] = = The condition Df (U V) 0 is not satisfied for neighboring nodes U and V when for the position p of node U the following is valid p mod (N-1) = 0 or p mod N = 0. 49

Case study 2: Folding equations and retiming General form of retiming inequalities: The general form of solution for r(p) is: The existence of this solution provides the retiming of DFG and allows the application of folding technique. 50

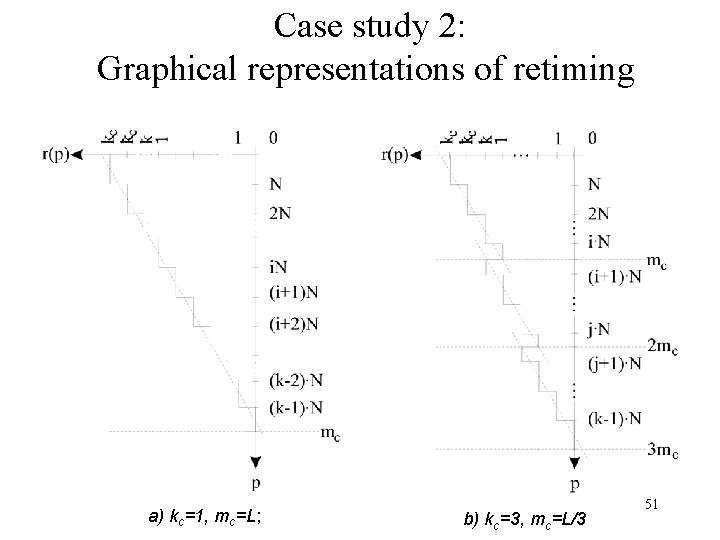
Case study 2: Graphical representations of retiming a) kc=1, mc=L; b) kc=3, mc=L/3 51

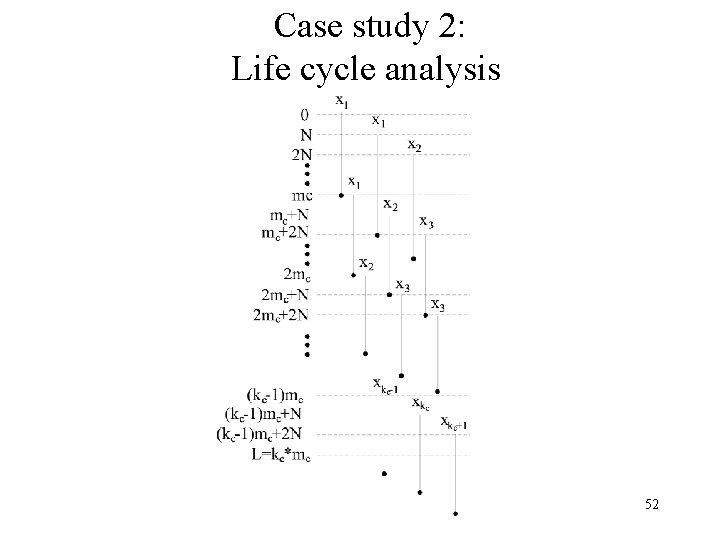
Case study 2: Life cycle analysis 52

Case study 2: General allocation table 53

Case study 2: Module for input data entering 54

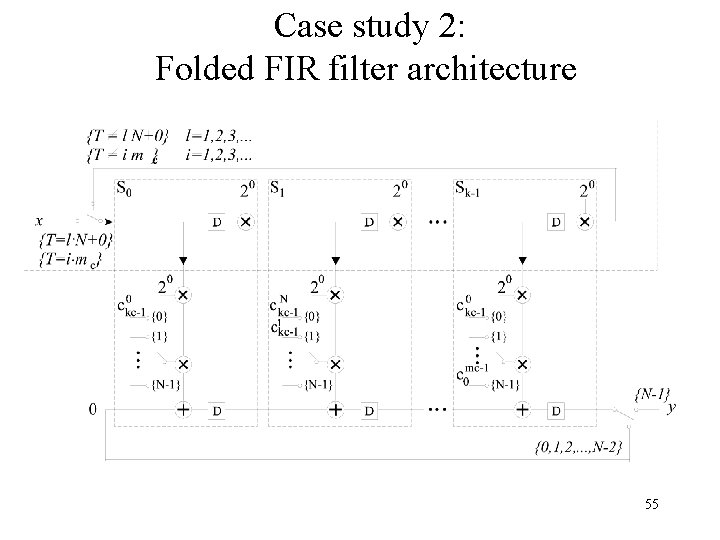
Case study 2: Folded FIR filter architecture 55

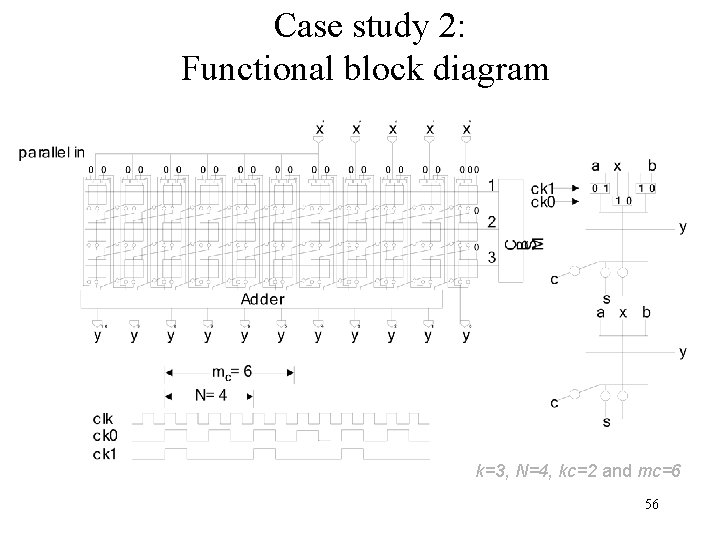
Case study 2: Functional block diagram k=3, N=4, kc=2 and mc=6 56

Case study 2: Data flow for folded architecture k=3, N=4, kc =2, mc=6 y 0= 20 c 00 x 0 + 21 c 01 x 0 +22 c 02 x 0 + 23 c 03 x 0 +24 c 04 x 0 + 25 c 05 x 0 = c 0 x 0 y 1= 20 c 10 x 0 + 21 c 11 x 0 +22 c 12 x 0 + 23 c 13 x 0 +24 c 14 x 0 + 25 c 15 x 0 +20 c 00 x 1 + 21 c 01 x 1 +22 c 02 x 1 + 23 c 03 x 1 +24 c 04 x 1 + 25 c 05 x 1 = c 1 x 0 +c 0 x 1 y 2= 20 c 10 x 1 + 21 c 11 x 1 +22 c 12 x 1 + 23 c 13 x 1 +24 c 14 x 1 + 25 c 15 x 1 + … + = c 1 x 1+ c 0 x 2 y 3= 20 c 00 x 2 + 21 c 01 x 2 +22 c 02 x 2 + 23 c 03 x 2 + … + = c 0 x 2+ c 1 x 3 57

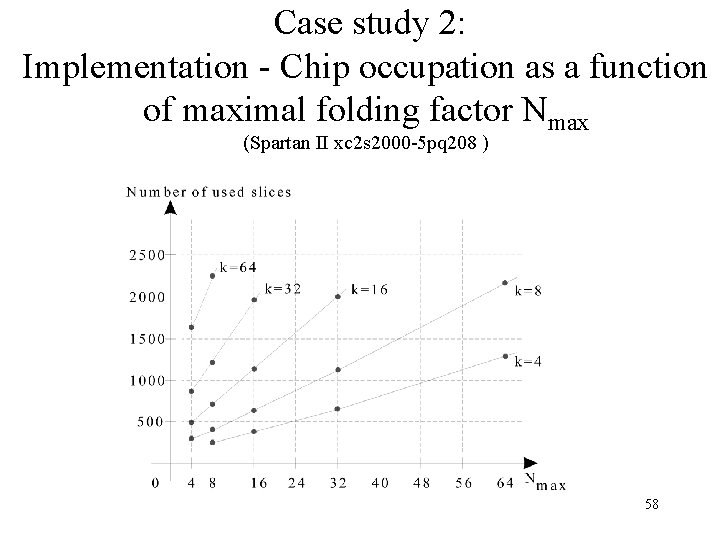
Case study 2: Implementation - Chip occupation as a function of maximal folding factor Nmax (Spartan II xc 2 s 2000 -5 pq 208 ) 58

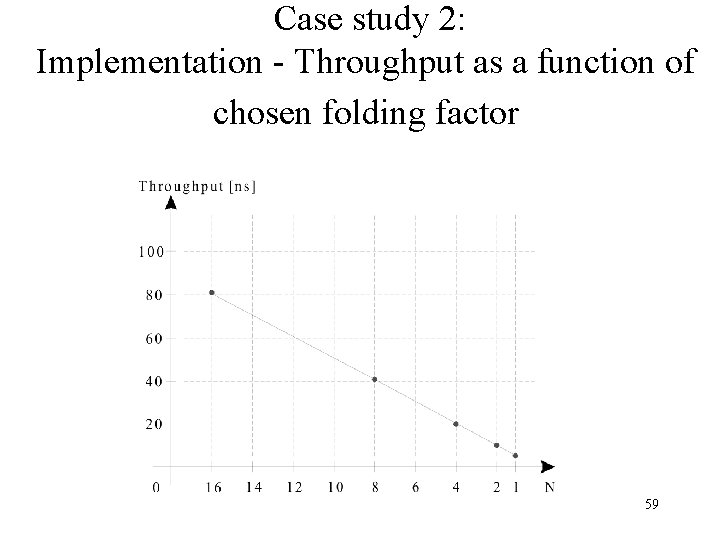
Case study 2: Implementation - Throughput as a function of chosen folding factor 59

Case study 2: Conclusions • Folding set assignment supports the changing of operations in folding sets. • The prerequisites for application of folding technique are satisfied. • Using of proposed folding set assignment, different operations can be mapped onto the different hardware units in the fixed structure array. 60

Case study 2: Conclusions • The derived folded processing array can be configured to perform FIR filtering with different number of taps and length of coefficients. • Synthesized architecture has kept desirable features of source architecture such as extensive pipelining, high regularity, truncation of LSBs of intermediate results without any loss of accuracy. • The number of basic cells is reduced to the number of basic cells in one plane of source architecture. • The obtained folded semi-systolic architecture is presented by DFG, allocation table, and data flow diagram. 61