Fluvial Hydraulics CH3 Uniform Flow Stable Channels Shear

Fluvial Hydraulics CH-3 Uniform Flow – Stable Channels

Shear Stress on Bed • Shear stress defined earlier as… • How does this equation simplify for channels with a large width? • Assume a trapezoidal channel… – Will shear stress on bed be larger or smaller than the shear stress on the sides of the channel?

Distribution of Shear Stress • Shear stress is distributed over the wetted perimeter, P – Graf gives the typical distribution for a trapezoidal channel (Chow, 1959) – derived from analytical and finite-difference methods – Pattern of distribution varies with shape of the section but unaffected by size of the section

Forces - Bottom of the Channel • Particles at bottom of channel resist shear stress of moving fluid… – Write a force balance equation at the moment of motion (incipient motion): David Chin, Water Resources Engineering
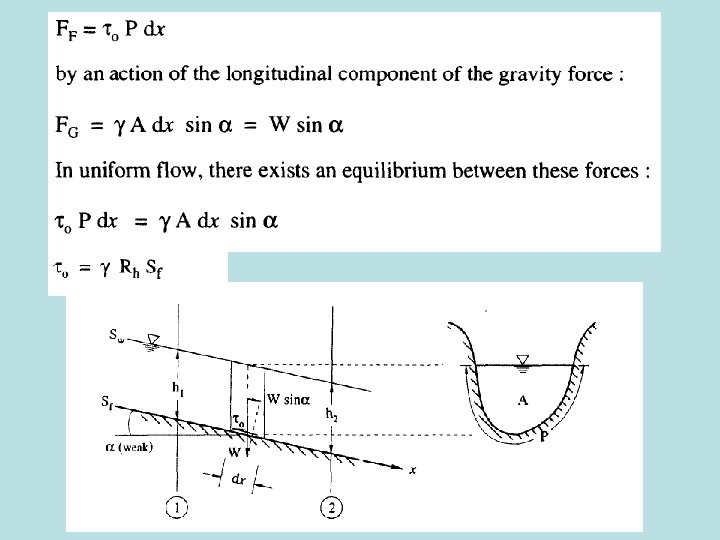

Forces on the Side of the Channel • Particles at side of channel resist shear stress of moving fluid and particle weight that acts down the side of the channel… – Total force tending to move particle: – Total force resisting motion:
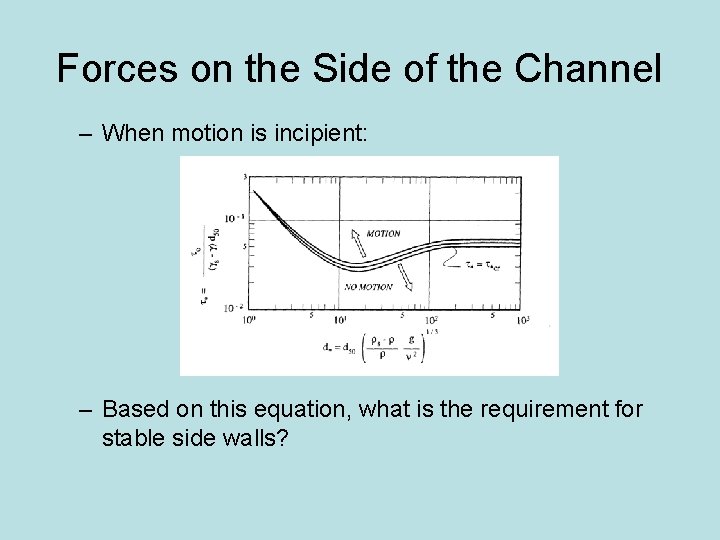
Forces on the Side of the Channel – When motion is incipient: – Based on this equation, what is the requirement for stable side walls?

Example 3. C A channel excavated in earth should convey a water discharge of Q = 57 m 3/s at an average temperature of 14 o. C. The bed slope is 0. 001; the banks have side slopes of 1. 5: 1 (H: V). A grain size analysis yielded d 50 = 37 mm, the angle of repose is 37 o, ss = 2. 65, and n = 0. 02. What should be the dimensions of this channel, if no erosion is allowed either at the bottom or on the banks?

Solution Methodology • Stability of banks requires q < j – Check using m… q = 33. 7 o • Calculate critical bed-shear stress on walls: – Need the critical shear stress – How?

Solution Methodology • Calculate a flow depth not to exceed these critical values: – Use minimum value of h based on shear stress on side walls – Actually should use an h smaller than this critical value

Solution Methodology • Last step is to solve for b: – Use Manning’s Equation with given Q – Use Table 1. 1 for A, Rh

Stable Section • Stable cross section – section in a channel with a mobile bed where there is no erosion over the entire wetted perimeter • Ideal stable cross section – stable cross section with a maximum discharge and a minimal wetted perimeter – Minimum water area, minimum top width, and maximum mean velocity minimum excavation

Stable Section • Assume a channel with a side wall angle at the water surface equal to the angle of repose: – To design a stable hydraulic section for maximum efficiency, it is necessary to create a condition of impending motion everywhere on channel bed
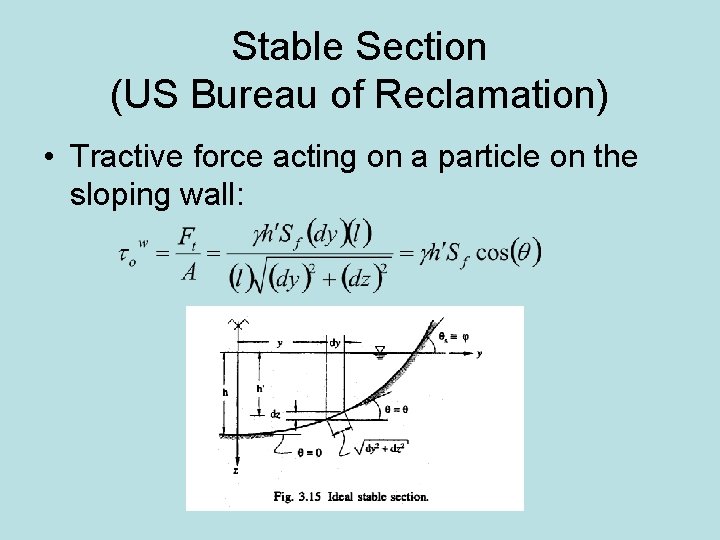
Stable Section (US Bureau of Reclamation) • Tractive force acting on a particle on the sloping wall:

Stable Section (US Bureau of Reclamation) • Condition of impending motion everywhere on bed: – Note the difference between h and h’

Stable Section (US Bureau of Reclamation) • The following differential equation is derived:
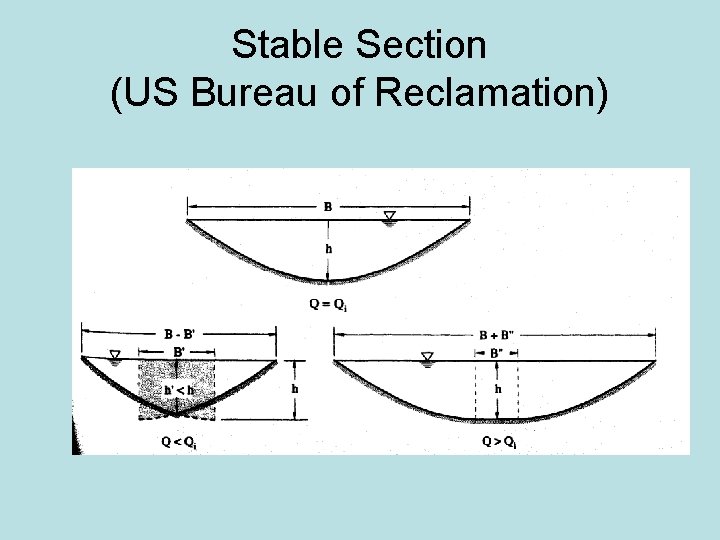
Stable Section (US Bureau of Reclamation)

Stable Section (US Bureau of Reclamation) • Other hydraulic parameters of the ideal cross section:
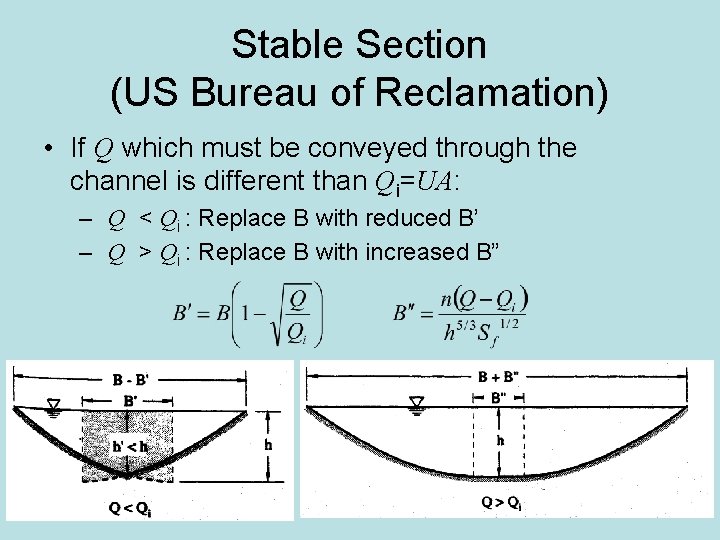
Stable Section (US Bureau of Reclamation) • If Q which must be conveyed through the channel is different than Qi=UA: – Q < Qi : Replace B with reduced B’ – Q > Qi : Replace B with increased B”

Example 3. C A channel excavated in earth should convey a water discharge of Q = 57 m 3/s at an average temperature of 14 o. C. The bed slope is 0. 001; the banks have side slopes of 1. 5: 1 (H: V). A grain size analysis yielded d 50 = 37 mm, the angle of repose is 37 o, ss = 2. 65, and n = 0. 02. What should be the dimensions of this channel, if no erosion is allowed either at the bottom or on the banks?



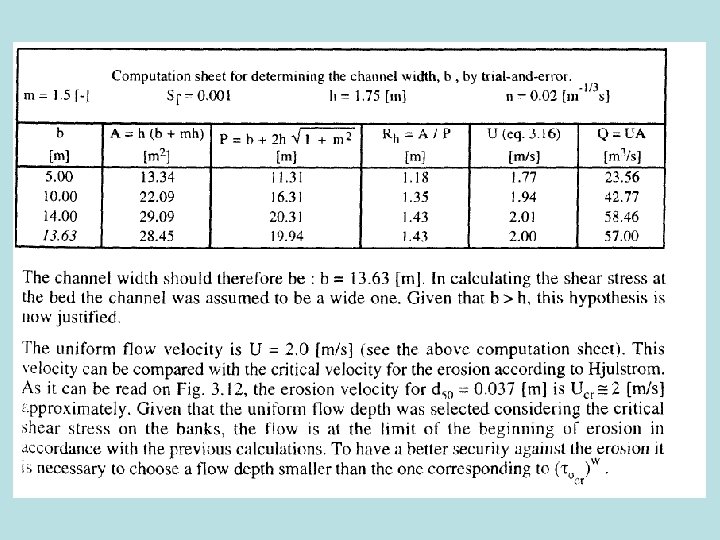

Example 3. D An artificial channel is constructed in a mountainous region and should convey 30 m 3/s at T=14 o. C without causing erosion. The slope of the channel will be 0. 01 and n = 0. 025. The grain size analysis has shown that the granular material is non-cohesive with d 50=50 mm, j = 37 o, and ss = 2. 65. (a) Determine dimensions of a rectangular channel with sides of wooden boards. (b) Determine the dimensions of an ideal stable cross section with the channel constructed of its bed material.

Solution Methodology • Use critical shear stress criteria: – Use Fig. 3. 13 (Shields diagram) to determine t*cr – Use t*cr to solve for tocr – Use the bed shear stress equation to solve for the hydraulic radius: – Use Manning’s equation to calculate U – Solve for A, P, b and h

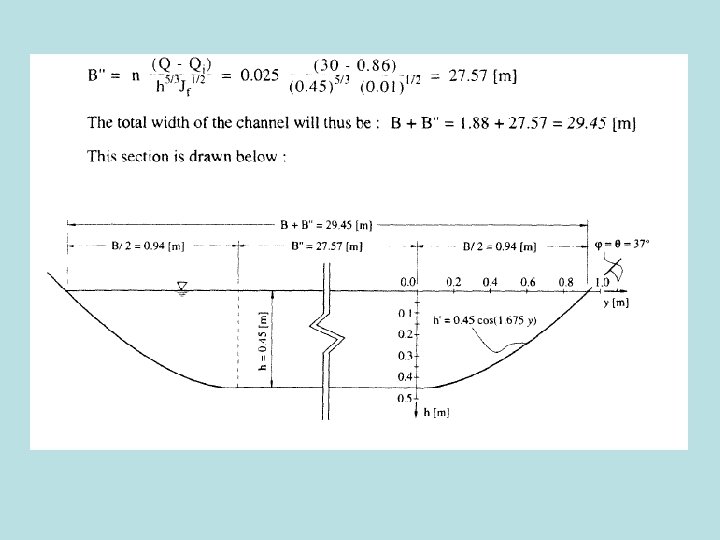
Solution Methodology • We need to first solve for h (maximum depth in the middle of the ideal crosssection): – Use critical shear stress from before to solve for tocr – Solve for h using:

Solution Methodology – Use equations for ideal cross-section to solve for h’, A, B, and U – Check the ideal discharge versus the actual discharge and adjust B if necessary

Example 3. D An artificial channel is constructed in a mountainous region and should convey 30 m 3/s at T=14 o. C without causing erosion. The slope of the channel will be 0. 01 and n = 0. 025. The grain size analysis has shown that the granular material is non-cohesive with d 50=50 mm, j = 37 o, and ss = 2. 65. (a) Determine dimensions of a rectangular channel with sides of wooden boards. (b) Determine the dimensions of an ideal stable cross section with the channel constructed of its bed material.





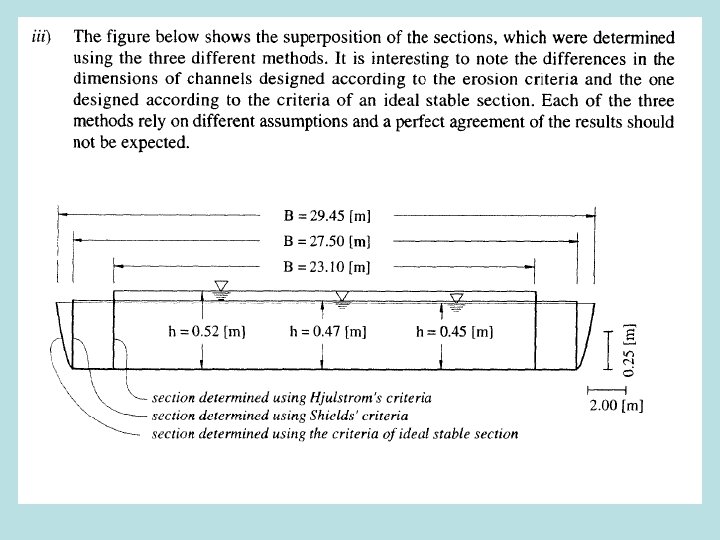
- Slides: 36