FLUIDA DINAMIS Aliran Laminer dan Turbulen Garis alir

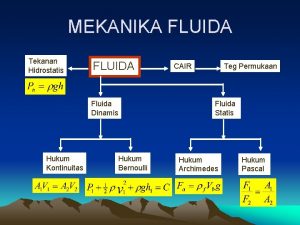
FLUIDA DINAMIS

Aliran Laminer dan Turbulen Garis alir pada fluida mengalir terdapat dua jenis, yaitu: 1. Aliran laminar adalah aliran fluida yang mengikuti suatu garis lurus atau melengkung yang jelas ujung dan pangkalnya serta tidak ada garis lu-rus yang bersilangan. 2. Aliran turbulen adalah aliran fluida yang ditandai dengan adanya aliran berputar dan arah gerak partikelnya berbeda, bahkan ber-lawanan dengan arah gerak keseluruhan fluida.

PERSAMAAN KONTINUITAS Apabila suatu fluida mengalir dalam sebuah pipa dengan luas penampang A dan kecepatan aliran fluidanya v, maka banyaknya fluida (volume) yang mengalir melalui penampang tersebut tiap satuan waktu dinamakan debit. Dalam bentuk persamaan debit dinyatakan sebagai berikut: dan Keterangan: Q = debit aliran fluida (m 3/s) V = volume fluida yang mengalir (m 3) t = waktu (s) v = kecepatan aliran fluida (m/s)

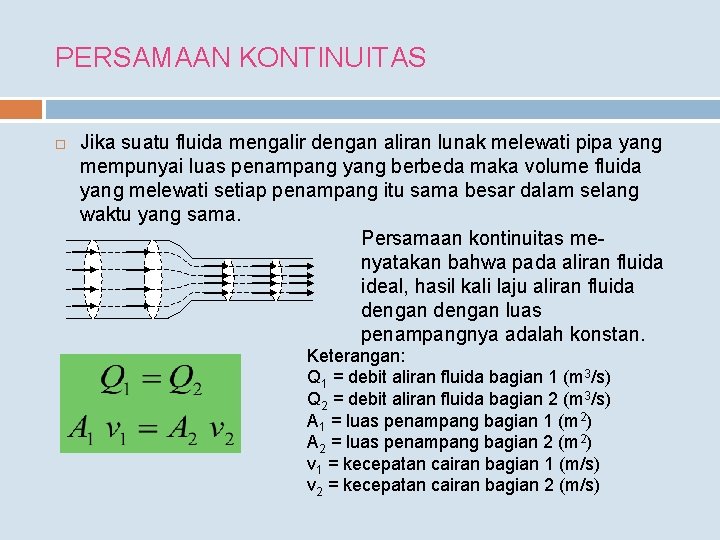
PERSAMAAN KONTINUITAS Jika suatu fluida mengalir dengan aliran lunak melewati pipa yang mempunyai luas penampang yang berbeda maka volume fluida yang melewati setiap penampang itu sama besar dalam selang waktu yang sama. Persamaan kontinuitas menyatakan bahwa pada aliran fluida ideal, hasil kali laju aliran fluida dengan luas penampangnya adalah konstan. Keterangan: Q 1 = debit aliran fluida bagian 1 (m 3/s) Q 2 = debit aliran fluida bagian 2 (m 3/s) A 1 = luas penampang bagian 1 (m 2) A 2 = luas penampang bagian 2 (m 2) v 1 = kecepatan cairan bagian 1 (m/s) v 2 = kecepatan cairan bagian 2 (m/s)

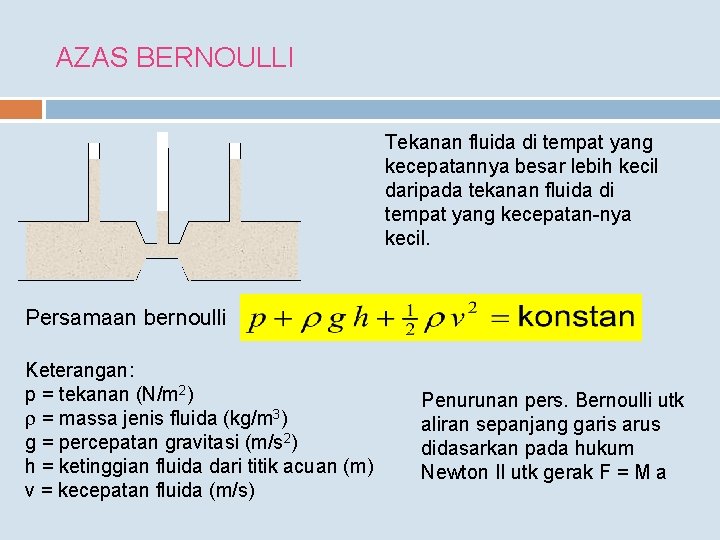
AZAS BERNOULLI Tekanan fluida di tempat yang kecepatannya besar lebih kecil daripada tekanan fluida di tempat yang kecepatan-nya kecil. Persamaan bernoulli Keterangan: p = tekanan (N/m 2) r = massa jenis fluida (kg/m 3) g = percepatan gravitasi (m/s 2) h = ketinggian fluida dari titik acuan (m) v = kecepatan fluida (m/s) Penurunan pers. Bernoulli utk aliran sepanjang garis arus didasarkan pada hukum Newton II utk gerak F = M a

AZAS BERNOULLI Terdapat dua kasus istimewa berkenaan dengan persamaan Bernoulli. 1. Fluida diam atau tidak mengalir (v 1 = v 2 = 0) Persamaan ini menyatakan tekanan hidrostatis dalam zat cair pada kedalaman tertentu. Keterangan: p 1 dan p 2 = tekanan pada titik 1 dan 2 (N/m 2) h 1 dan h 2 = tinggi tempat 1 dan 2 (m) r = massa jenis fluida (kg/m 3) g = gravitasional acceleration (m/s 2)

AZAS BERNOULLI 2. Fluida mengalir pada pipa horisontal (h 1 = h 2 = h) Persamaan ini menyatakan jika v 2 > v 1, maka p 1 > p 2 yang berarti jika kecepatan aliran fluida disuatu tempat besar maka tekanan fluida di tempat tersebut kecil dan berlaku sebaliknya. Keterangan: p 1 dan p 2 = tekanan pada titik 1 dan 2 (N/m 2) v 1 dan v 2 = kecepatan pada 1 dan 2 (m) r = massa jenis fluida (kg/m 3) g = gravitasional acceleration (m/s 2)

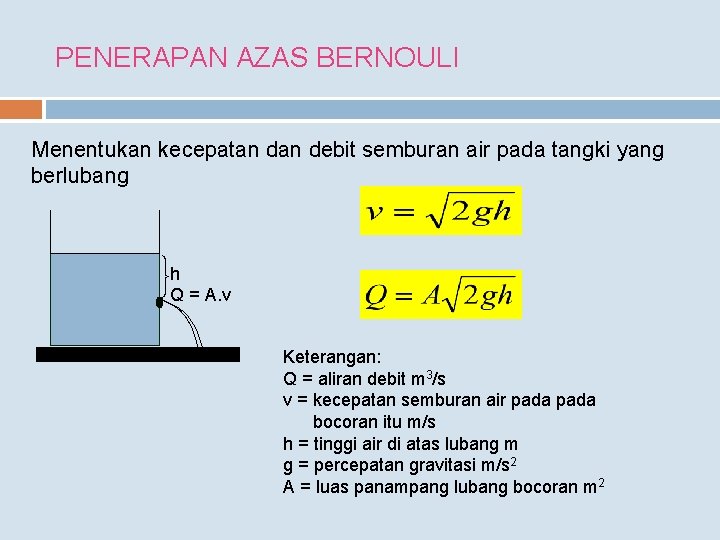
PENERAPAN AZAS BERNOULI Menentukan kecepatan debit semburan air pada tangki yang berlubang h Q = A. v Keterangan: Q = aliran debit m 3/s v = kecepatan semburan air pada bocoran itu m/s h = tinggi air di atas lubang m g = percepatan gravitasi m/s 2 A = luas panampang lubang bocoran m 2

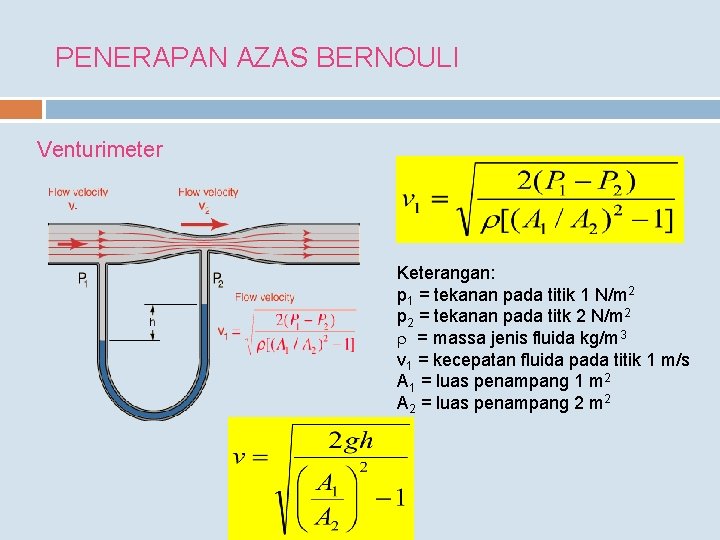
PENERAPAN AZAS BERNOULI Venturimeter Keterangan: p 1 = tekanan pada titik 1 N/m 2 p 2 = tekanan pada titk 2 N/m 2 r = massa jenis fluida kg/m 3 v 1 = kecepatan fluida pada titik 1 m/s A 1 = luas penampang 1 m 2 A 2 = luas penampang 2 m 2

PENERAPAN AZAS BERNOULI Tabung pitot merupakan alat yang digunakan untuk mengukur kecepatan aliran suatu zat cair.

Contoh soal : Sebuah tempat air yang sangat besar mempunyai sebuah kran yang luas penampangnya 2 cm 2. Jika tinggi permukaan air dari kran 3, 2 m. Hitunglah air yang tertampung di ember selama 10 detik