Fluid Mechanics Pressure and Pascals Law States of

Fluid Mechanics: Pressure and Pascal’s Law

States of Matter l Solid l l Liquid l l Has a definite volume and shape Has a definite volume but not a definite shape Gas – unconfined l Has neither a definite volume nor shape

Fluids l l A fluid is a collection of molecules that are randomly arranged and held together by weak cohesive forces and by forces exerted by the walls of a container. Both liquids and gases are fluids.

Statics and Dynamics with Fluids l Fluid Statics l l Fluid Dynamics l l Describes fluids at rest, i. e. in equilibrium Describes fluids in motion The same physical principles that have applied to statics and dynamics up to this point will also apply to fluids

Forces in Static Fluids l The only force that can be exerted on an object submerged in a static fluid is one that tends to compress the object from all sides. l The force exerted by a static fluid on an object (or on the walls of the container) is always perpendicular to the surface of the object.

Pressure l The pressure P of the fluid is the ratio of (the value of the force) to (the area): l Unit of pressure is pascal (Pa): l Normal atmospheric pressure: 1 atm = 1. 013 x 105 Pa

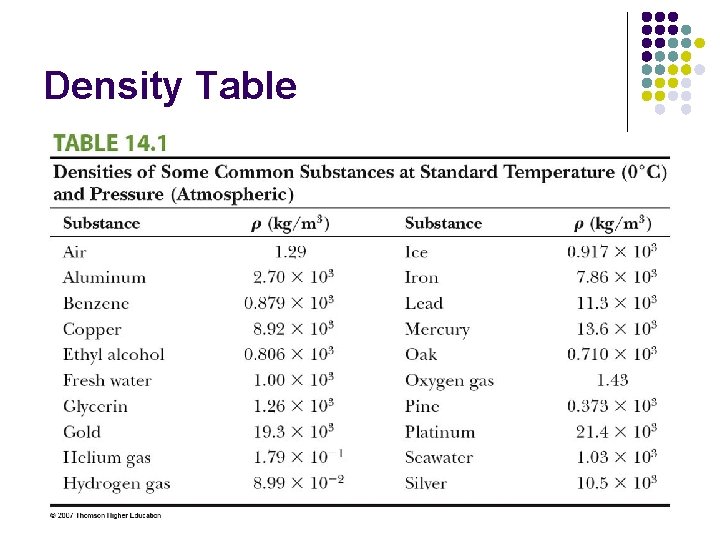
Density Notes l l l Just as pressure replaces force when we describe fluids, density replaces mass. Density = mass per unit volume of the substance. The values of density for a substance vary slightly with temperature since volume is temperature dependent.

Density Table

Variation of Pressure with Depth l l l Pressure within a fluid varies with depth. If a fluid is at rest in a container, all portions of the fluid must be in static equilibrium. All points at the same depth must be at the same pressure. l Otherwise, the fluid would not be in equilibrium

Pressure and Depth l Examine the darker region, a sample of liquid within a cylinder l The pressure at the bottom section is greater due to the weight of the fluid l l The pressure P at a depth h below the surface of the fluid is l l DP = rg. Dh P = P 0 + rgh If the liquid is open to the atmosphere, P 0 = 1. 00 atm = 1. 013 x 105 Pa.

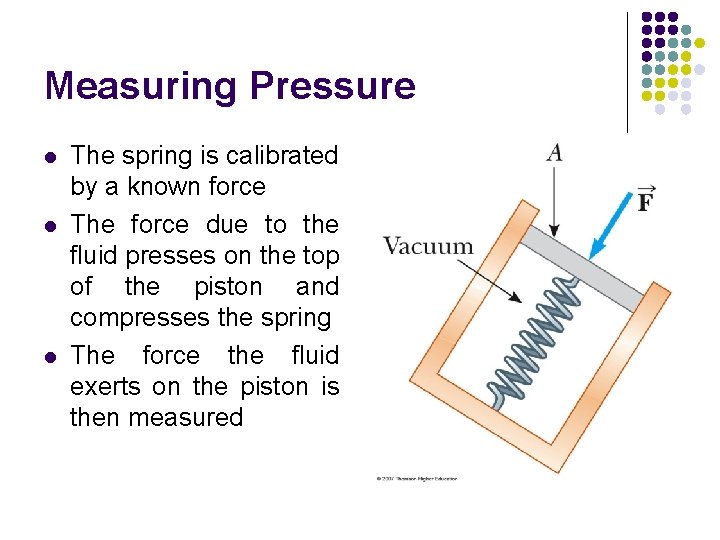
Measuring Pressure l l l The spring is calibrated by a known force The force due to the fluid presses on the top of the piston and compresses the spring The force the fluid exerts on the piston is then measured

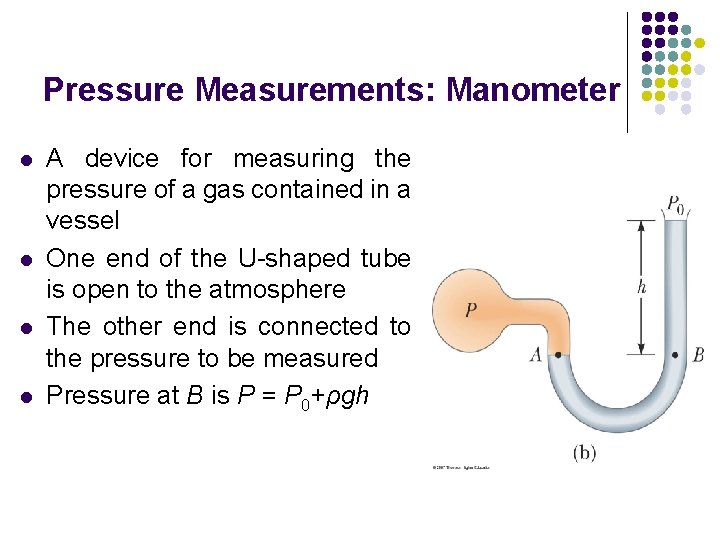
Pressure Measurements: Manometer l l A device for measuring the pressure of a gas contained in a vessel One end of the U-shaped tube is open to the atmosphere The other end is connected to the pressure to be measured Pressure at B is P = P 0+ρgh

Absolute vs. Gauge Pressure l l l P = P 0 + rgh P is the absolute pressure The gauge pressure is the difference P – P 0 l l This is also rgh This is what you measure in your tires

Pressure Measurements: Barometer l l Invented by Torricelli A long closed tube is filled with mercury and inverted in a dish of mercury l l l The closed end is (nearly) a vacuum Measures atmospheric pressure as Po = r. Hggh One 1 atm = 0. 760 m (of Hg)

Pascal’s Law l A change in the pressure applied to a fluid is transmitted to every point of the fluid and to the walls of the container l This is a consequence of the previous equation, P = P 0 + rgh

The Hydraulic Press l A large output force can be applied by means of a small input force. l The volume of liquid pushed down on the left must equal the volume pushed up on the right

Fluid Mechanics: Archimedes’ Principle

Buoyant Force - Archimedes’ Principle l The buoyant force (B) is the upward force exerted by a fluid on any immersed object. l B = weight of DISPLACED FLUID l The only forces acting on the object are its own weight and the buoyant force. They decide what happens.

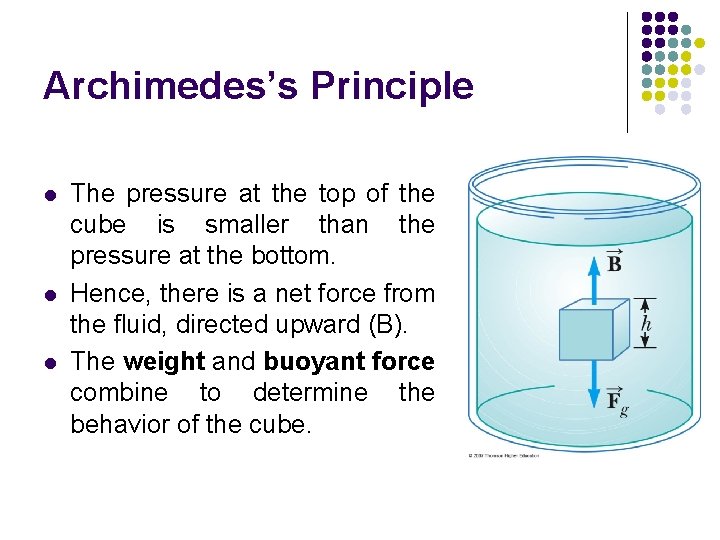
Archimedes’s Principle l l l The pressure at the top of the cube is smaller than the pressure at the bottom. Hence, there is a net force from the fluid, directed upward (B). The weight and buoyant force combine to determine the behavior of the cube.

1. Totally Submerged Object l An object of volume V and density robject is totally submerged in a fluid of density rfluid l The downward gravitational force is Fg = ( robject Vobject ) g l The upward buoyant force is: B = ( rfluid Vdisplaced fluid )g = (rfluid Vobject )g

Totally Submerged Object l B>W B<W The direction of the motion of an object in a fluid is determined only by the densities of the fluid and the object. l Fg = ( robject Vobject ) g vs. B = (rfluid Vobject )g boils down to robject vs. rfluid

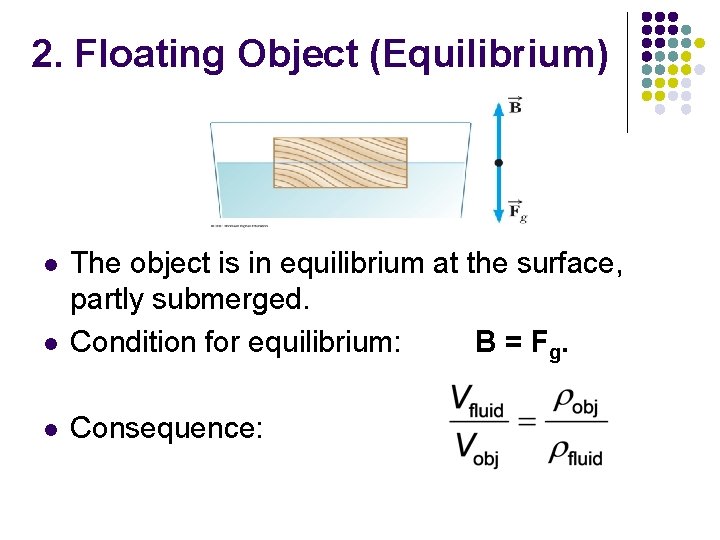
2. Floating Object (Equilibrium) l The object is in equilibrium at the surface, partly submerged. Condition for equilibrium: B = F g. l Consequence: l

Archimedes and the Crown By measuring the weight of the crown in air, and then submerged in water, the density of the crown can be found.

Archimedes and the Crown l l Archimedes was (supposedly) asked, “Is the crown made of pure gold? ” Crown’s weight in air = 7. 84 N Weight in water (submerged) = 6. 84 N Buoyant force will equal the apparent weight loss l Difference in readings will be the value of the buoyant force

Archimedes and the Iceberg l l l Vice is the total volume of the iceberg Vwater is the volume of the water displaced, equal to the volume of the submerged part of the iceberg About 89% of the ice is below the water’s surface

Archimedes and the Iceberg l l What fraction of the iceberg is below water level? The iceberg is only partially submerged and so

Archimedes and Floating l Object floats, partly submerged: robject < rfluid B=W

Archimedes and Sinking l Object sinks: robject > rfluid B < W, and Wapparent = W - B