FLUID FLOW CONTINUITY Bernoullis Principle FLUID FLOW CONTINUITY

FLUID FLOW CONTINUITY Bernoulli’s Principle

FLUID FLOW CONTINUITY Usually, liquids are considered “incompressible”, meaning that the density of the liquid remains nearly constant. Gases are easily compressed, like air in a tire or air compressor.

CONT. As a liquid flows from one container to another, the mass of liquid flowing from one section to another is equal, the density is equal, the volume is equal…etc…THEY ARE EQUAL

BERNOULLI’S EQUATION Bernoulli’s equation is the conservation of energy applied to a moving fluid. As fluid moves from one chamber to another or from one high to another work is done. BERNOULLI’S EQUATION P 1+1/2ρV 12 +ρgh 1 = P 2 + 1/2ρV 22 + ρgh 2 P=pressure Ρ=density of the fluid V = the speed of the fluid g= acceleration due to gravity h =is the height of the fluid

CONSIDER THIS A tank filled with fluid, as shown , is open at the top and has a hole in the side. The cylinder is small so the change in height does not cause a great deal of difference in pressure. The speed that the fluid moves in the tank is much smaller than the speed of the fluid coming out of the hole. So much smaller we can consider Vel tank or V 1=0 m/s

CONSIDER CONT. Applying these conditions to Bernoulli’s Equation to solve for V 2, we write

ANSWER P 1 +1/2 ρ (0) +ρgh 1 = P 2 +1/2 ρV 22 +ρgh 2 Subtracting P 1 from both sides: Ρgh 1 = ½ ρV 22 +ρgh 2 Divide by ρ on both sides: gh 1= 1/2 V 22 +gh 2 Solving for V 2: V 2= √ 2 g (h 1 -h 2)

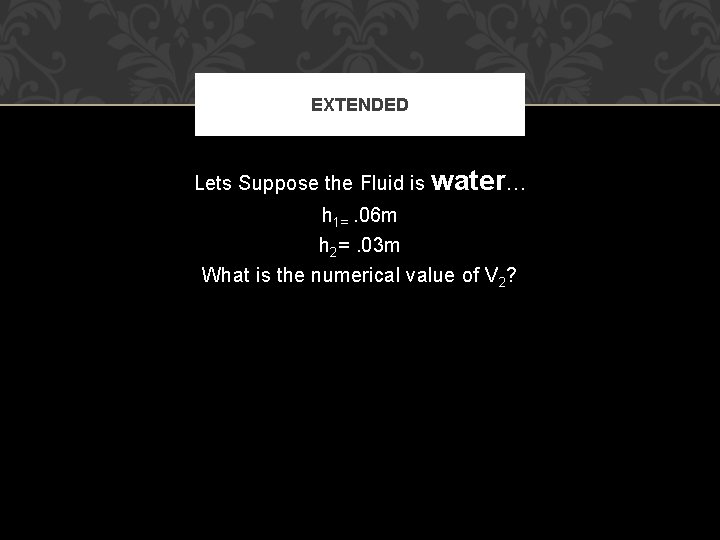
EXTENDED Lets Suppose the Fluid is water… h 1=. 06 m h 2=. 03 m What is the numerical value of V 2?

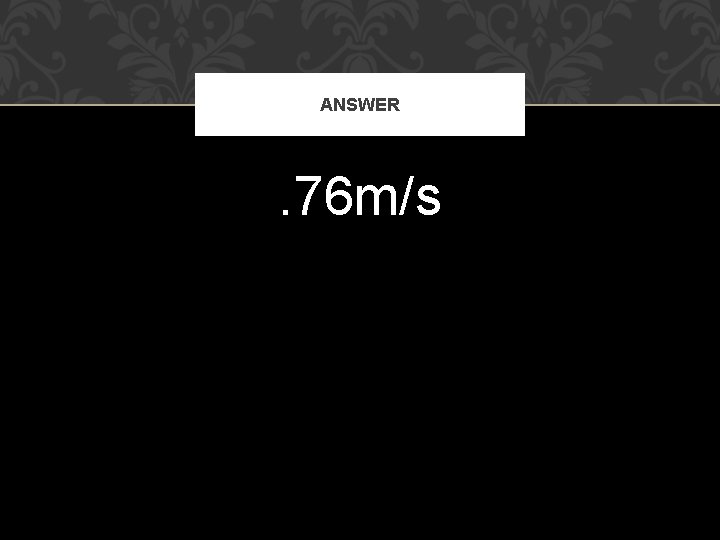
ANSWER . 76 m/s